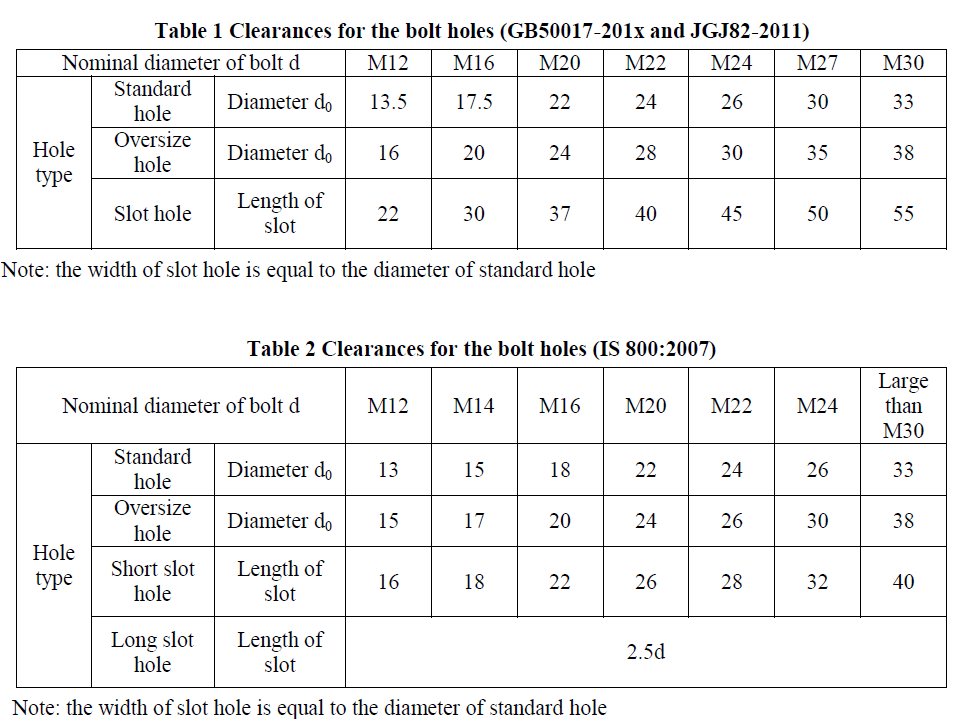
ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Pavithra C 1 Dr. S. Bhargavi2 Student, Department of Electronics and Communication, S.J.C. Institute of Technology,Chickballapur,Karnataka,India1 Professor, Department of Electronics and Communication, S.J.C. Institute of echnology,Chickballapur,Karnataka,India2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper we have presented a method for fusing two dimensional multi-resolution 2-D images using wavelet transform under the combine gradient and smoothness criterion. The usefulness of the method has been illustrated using various experimental image pairs such as the multi- focus images, multi-sensor satellite image and CT and MR images of cross-section of human brain. The results of the proposed method have been compared with that of some widely used wavelet transform based image fusion methods both qualitatively and quantitatively. Experimental results reveal that the proposed method produces better fused image than that by the latter. The use of both gradient and relative smoothness criterion ensures two fold effects. While the gradient criterion ensure that edges in the images are included in the fused algorithm, the relative smoothness criterion ensures that the areas of uniform intensity are also incorporated in the fused image thus the effect of noise is minimized. It should be noted that the proposed algorithm is domain-independent
Keywords |
| image fusion, wavelet transform, fused images, wavelet based fusion, multi-resolution |
INTRODUCTION |
| Image fusion is the process by which two or more images are combined into a single image retaining the important features from each of the original images. The fusion of images is often required for images acquired from different instrument modalities or capture techniques of the same scene or objects (like multi-sensor, multi-focus and multimodal images). For example, in multi-focus imaging one or more objects may be in-focus in a particular image, while other objects in the scene may be in focus in other images. For remotely sensed images, some have good spectral information whereas others have high geometric resolution. In the arena of biomedical imaging, two widely used modalities, namely the magnetic resonance imaging (MRI) and the computed tomography (CT) scan do not reveal identically every detail of brain structure. While CT scan is especially suitable for imaging bone structure and hard tissues, the MR images are much superior in depicting the soft tissues in the brain that play very important roles in detecting diseases affecting the skull base. These images are thus complementary in many ways and no single image is totally sufficient in terms of their respective information content. The advantages these images may be fully exploited by integrating the complementary features seen in different images through the process of image fusion that generates an image composed of features that are best detected or represented in the individual images. Important applications of the fusion of images include medical imaging, microscopic imaging, remote sensing, computer vision, and robotics. The first step toward fusion, which may be interpreted as a preprocessing step is the registration which brings down the constituting images to a common coordinate system as fusion of images is meaningful only when common objects in images have identical geometric configuration with respect to size, location and orientation in all the images. In the next step, the images are combined to form a single fused image through a judicious selection of proportions of different features from different images. Fusion techniques include the simplest method of pixel averaging to more complicated methods such as principal component analysis and wavelet transform fusion. Several approaches to image fusion can be distinguished, depending on whether the images are fused in the spatial domain or they are transformed into another domain, and their transforms fused. Li et al. [1] have suggested a multisensory image fusion using wavelet transform in which a cascaded sequence of forward and reverse wavelet transform on multimodal images produces a fused image. Other common wavelet transform based fusion schemes include maximum selection (MS) just picks the wavelet transform coefficient in each sub-band with the largest magnitude. Burt and Kolczynski used a normalized correlation between the two imagesâ sub bands over a small local-area and the resultant coefficient for reconstruction is calculated from this measure via a weighted average of the two imagesâ coefficients. Zu Shu-long [7] proposed wavelet based fusion approach using „gradientâ criteria, while Hill et al. [6] achieved fusion through the application of the shift invariant and directionally selective Dual Tree Complex Wavelet Transform (DT-CWT). In this paper, an image fusion algorithm based on wavelet transform is proposed. In the proposed scheme, the images to be processed are decomposed into sub-images with the same resolution at same levels and different resolution at different levels and then the information fusion is performed using high-frequency sub-images under the combined „gradientâ and „ relative smoothnessâ criterion and finally these sub-images are reconstructed into a resultant image having plentiful information. The developed scheme is applied to fuse multi-focus, multi-modal and remotely sensed multi-sensor images. Any kind of image fusion method involves registration as a first and foremost step. In general, different sensors respond to scene characteristics in different and, partially, complementary ways. |
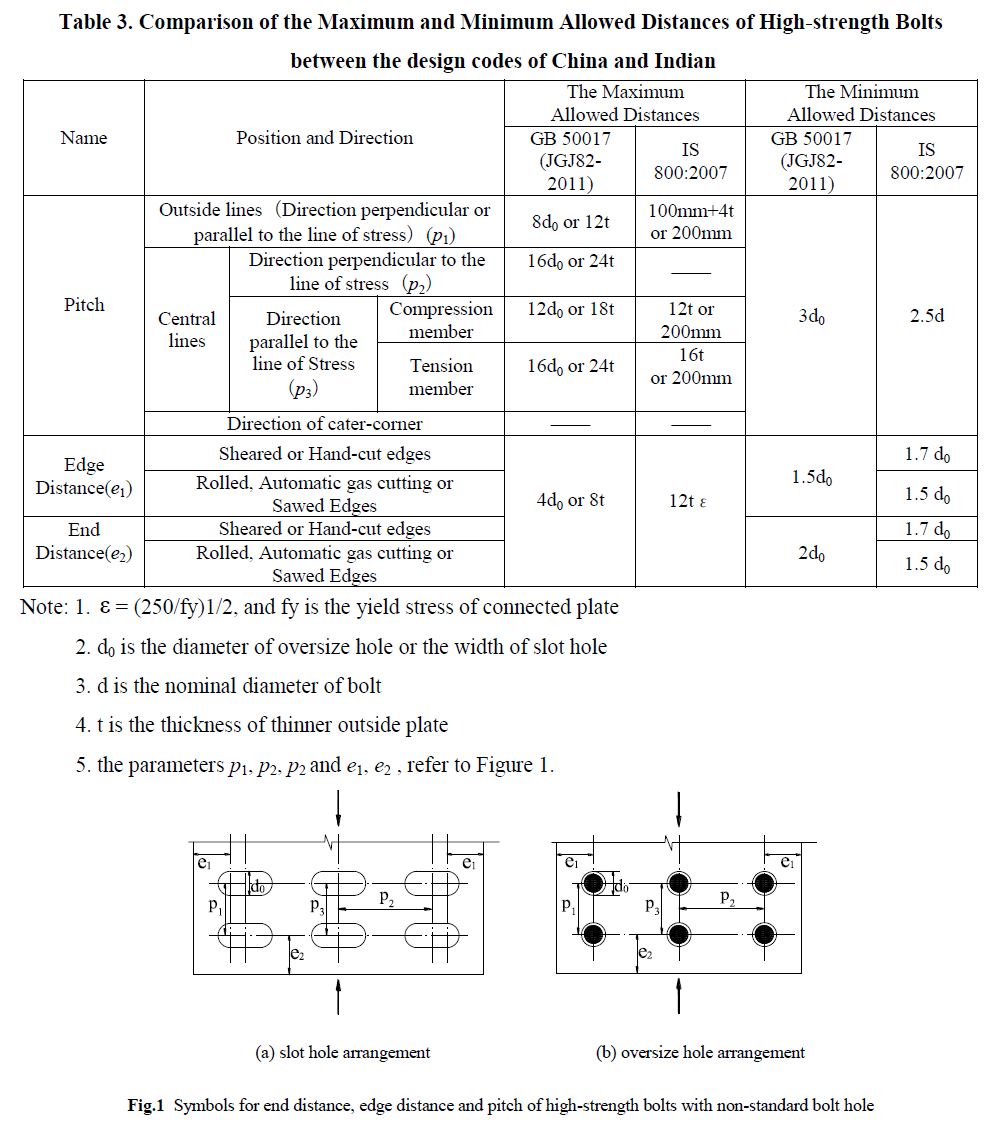
II. WAVELET TRANSFORM AND WAVELET BASED FUSION |
| Wavelet transform is a powerful mathematical tool used in the fields of signal processing. It is used to divide the given function or signal into different scale components such that each scale component can be studied with a resolution that it matches. Mallat used the wavelets to be the foundation of new powerful approach to signal processing and analysis called the Multi-resolution Theory. The same approach has been extended to multi-dimensional signal decomposition. |
| In a multi-focus and multi-sensor image acquisition system, the size, orientation and location of an object relative to its „ownâ background may not be identical in all the images of different modalities. Integration or fusion of multi-focus or multi-sensor information is possible only if the images are registered or positioned with respect to a common coordinate system. Image registration (in case of fusing two images) is the process of determining correspondence between all points in two images of the same scene or object. The most common form of transform image fusion is wavelet transform fusion. In common with all transform domain fusion techniques the transformed images are combined in the transform domain using a defined fusion rule then transformed back to the spatial domain to give the resulting fused image. Wavelet transform fusion is more formally defined by considering the wavelet transforms „wâ of the „nâ registered input images Ij(x,y), j=1,2…n together with the fusion rule „fâÂÂ. Then, the inverse wavelet transform w-1 is computed, and the fused resulting image I(x,y) is reconstructed as depicted in figure 1. |
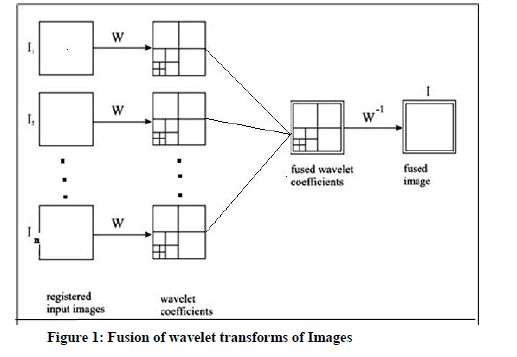 |
III. PROPOSED IMAGE FUSION ALGORITHM |
| We propose a scheme for fusion of „nâ registered set of images of same scene obtained through different modalities. The basic idea is to decompose each registered image into sub-images using forward wavelet transform which have same resolution at same level and different resolution at different levels. Information fusion is performed based on the high frequency (detailed coefficients) sub-images and resulting image is obtained using inverse wavelet transform. The proposed scheme uses two criterions namely the „gradientâ and „smoothnessâ measure which we discuss first. |
| A. THE GRADIENT CRITERION |
| Given a gray image I(x, y), the gradient at any pixel location (x, y) is obtained by applying two dimensional direction |
 |
| The gradient magnitude and two fast decreasing approximations can be obtained as: |
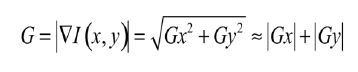 |
| B The Relative Smoothness Criterion |
| The second criterion of relative smoothness uses the statistical moments of gray-level histogram of the region in the neighborhood of the pixel (x, y). Let z be the random variable denoting gray levels and p(zi), i=1, 2…L-1, be the corresponding histogram of the region in the neighborhood of pixel (x, y), where L is the number of distinct gray levels. The second moment or variance of z about mean is given by |
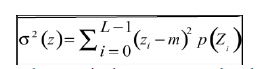 |
| where m is the mean gray level of z given by |
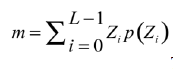 The measure for relative smoothness in the neighborhood of pixel (x, y) can be thus established as The measure for relative smoothness in the neighborhood of pixel (x, y) can be thus established as |
| C. IMAGE FUSION |
| Let I1(x, y), I2(x, y), in(x, y) be the n registered images to be fused. The decomposed low frequency also referred to as the approximation coefficient sub-images be lI1j(x,y), lI2j(x,y), … lInj(x,y) and decomposed high frequency also called as the detailed coefficients be hI1j k(x,y,), hI2j k(x,y), … hInj k(x,y) respectively, where „jâ is the parameter of resolution, j=1,2…J and for every „jâÂÂ, âÂÂkâ = 1,2,3 which represent directional sensitive wavelet decomposition namely along horizontal, vertical and diagonal directions. For every even parameter of resolution i.e. j=2, 4…J, the magnitude of the gradient of the image generated from the high frequency components be GIijk(x, y), i=1, 2…n. For every odd parameter of resolution i.e. j=1, 3, J, the relative smoothness of the image generated from the high frequency components be RIij k(x, y), i=1, 2…n. The fused high frequency sub-images are evaluated as: |
| In k(x,y)= hIpj k(x,y) |
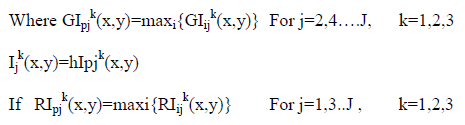 |
| The fused low frequency sub-images are: |
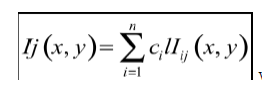 where ci is the parameter which determine the contribution from each image. where ci is the parameter which determine the contribution from each image. |
| Using the inverse wavelet transform, and fused high and low frequency components evaluated above we reconstruct the image. This reconstructed image has information integrated from all the different images sources. This scheme shows the high frequency image fusion between images under the combined gradient and relative smoothness criterion. |
| The same method can be used for fusing colored images. We can covert the colored images from RGB (Red, Green, Blue) to HIS (Hue, Saturation, Intensity) space and process only the Intensity component of the HIS space to acquire the fused image. |
IV. DISCUSSION AND ANALYSIS |
| A. THE CORRELATION MEASURE |
| The fusing ability of the algorithm is measured quantitatively by means of, say, pixel-gray-level correlation between two images. The correlation between two images f(x, y) and g(x,y) is defined as |
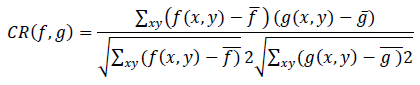 |
| And N is the total number of pixels in either of the images. The Haar Wavelet was used as the mother wave and the resolution parameter ‘j’ was taken up to 6. The use of Haar wavelet was for the ease of implementation. Our aim was to go for a multi-resolution description of the image prior to fusion for which we need a filter, without loss of generality we chose Haar Wavelet.The fused image enjoys relatively high correlation with either of the images. This implies features of both the images are transported to the fused image. |
| We did not restrict our algorithm to work on any specific type/class of images.Equal contribution of each low frequency subimage was considered in the experiments. In the first experiment a pair of multi-focus image was taken. In figure 2(a) the clock in front is in focus while in figure 2(b) the clock at the back is focused. Figure 2(c) shows the image obtained after fusion. CT-MR image pair was taken up for second experiment. Figure 3(a) is the CT image of the human brain showing bones and hard tissue. Figure 3(b) is the MR image showin soft tissues.The fused CT-MR image is shown in figure3(c). |
 |
 |
| Figure 4: (a) fused image under proposed scheme, (b) fused image under MS scheme, (c) fused image under GS scheme, (d) fused image under WA scheme |
| In our experiment the computed values of CR (FuseImg, OrgImg1), CR (FuseImg, OrgImg2) and CR (OrgImg1, OrgImg2) is computed and is shown in TABLE I below. |
 |
| The fused image enjoys relatively high correlation with either of the images. This implies features of both the images are transported to the fused image. |
| B. COMPARISON WITH EXISTING FUSION ALGORITHMS |
| Wavelet based image fusion is one of the most commonly used methods to achieve image fusion. Many different schemes have been proposed for the same. The following three previously developed fusion rule schemes were implemented using discrete wavelet transform based image fusion and the results were compared with the proposed scheme. |
| (1) Maximum selection (MS) scheme: This simple scheme just picks the coefficient in each sub-band with the largest magnitude. |
| (2) Weighted average (WA) scheme: The resultant coefficient for reconstruction is calculated from weighted average of the two imagesâ coefficients. |
| (3) Gradient criterion selection (GS) scheme: This was proposed by Zhu Shu-long in [7]. The scheme picks the coefficient in each sub-band with the largest magnitude of the gradient defined over the neighborhood. Correlation coefficient is estimated by as shown above equation and compare with existing techniques. The comparative results of measure of correlation are shown in the below TABLEII. |
 |
V. CONCLUSIONS |
| The fusion of images is the process of combining two or more images into a single image retaining important features from each of the images. A scheme for fusion of multi-resolution 2D gray level images based on wavelet transform is presented in this project. If the images are not already registered, a point-based registration, using affine transformation is performed prior to fusion. The images to be fused are first decomposed into sub images with different frequency and then information fusion is performed using these images under the proposed gradient and relative smoothness criterion. Finally these sub images are reconstructed into the result image with plentiful information. A quantitative measure of the degree of fusion is estimated by cross-correlation coefficient and comparison with some of the existing wavelet transform based image fusion techniques is carried out. It should be noted that the proposed algorithm is domainindependent. That means it uses knowledge of neither the imaging device nor the objects being imaged. Therefore, it can be applied to fusion of different kinds of multi-modal images. Second, as the actual fusion is done during the construction of modified coefficients, the scheme has been extended to fusion of „nâ images as already proposed in the algorithm. As stated earlier we can use the same method for fusing colored images. We can covert the colored images from RGB (Red, Green, Blue) to HIS (Hue, Saturation, Intensity) space and process only the Intensity component of the HIS space to acquire the fused image However, our method is computationally more expensive and needs more space for implementation. We wish to extend our work for fusing multi-resolution images. |
References |
|