ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
R.Thulasiram#1, Ms.S.Rajeswari*
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Harmonic pollution is one of the major issue in the modern power system. The harmonic pollution affects the power stability of industries and consumers. As the power system network are expanding more and more, it necessitates responsive detection of harmonic source and accurate identification of harmonic disturbances in order that remedial measures can be taken for the improvement of power quality. This paper presents a new method based on discrete wavelet transform for the detection of harmonic source and identification of harmonic content. It is based on the analysis of detail active power measurement approach. The detail active powers at the lowest level along with the details pollution factor have been used to clearly identify the location of the harmonic source. The simulation results presented here show that the proposed method can effectively indicate the presence of nonlinear load under both sinusoidal and distorted supplies and can also detect the dominant source of harmonic pollution in power system network.
Keywords |
| power uality,harmonics,wavelettransform Detection of harmonic sources. |
INTRODUCTION |
| With the increased use of non linear loads like power electronic switches and computer controlled devices there has been an increase in voltage and current distortion in the distribution network. The presence of voltage and current distortion is harmful to the equipment connected in the power system network. Harmonics can be produced by the loads only, by the source only or by both the source and the load. The power component definitions contained in IEEE Standard 1459-2000 has been reformulated using discrete wavelet transform in both single phase [2] and three phase [3] systems. The measurement of power components using stationary wavelet transform keeps all time characteristics of the nonstationary waveform while providing different frequency resolutions [4]. The time domain strategy [5] for the detection of fundamental and harmonic components of voltages and currents is able to evaluate all the quantities of IEEE Standard 1459-2000. |
| Harmonic pollution source detection is the first step towards improving the power quality of the network. The total harmonic power method [13,14] is the method for the identification and measurement of harmonic pollution in radial and non radial systems. The signs of total and individual harmonic powers can provide detailed information about the harmonic pollution [15]. |
| Wavelet packet transform can be used for power calculations of both fundamental and harmonics of signal [16]. At each wavelet decomposition level the squared value of the detail information is calculated as their energy to construct the feature vector for analysis. Multiwavelet transform is a powerful tool for the recognition of power quality disturbances [18]. Accurate detection, classification and location of faults are of great importance for economic operation of power systems [19– 21]. Wavelet transform can also be of great assistance for digital differential protection [22] and voltage sag detection [23]. An approach to select the most suitable mother wavelet to achieve accurate measurement of steady state harmonic distortion has been presented in [25]. |
| This paper proposes a new strategy that is able to locate dominant harmonic source upstream or downstream from the metering section. In this paper first the theoretical formulation and implementation of the proposed strategy is presented. Then validation of the strategy is carried out on a simple test system which has been developed to simulate both sinusoidal and nonsinusoidal supplies with both linear and nonlinear loads. The active power signal has been considered and discrete wavelet transform has been used to get the detail active power at different levels of resolution. It has been verified that signs of the detail powers can detect the location of the dominant source of harmonic pollution. This method can clearly identify whether the harmonic pollution is due to the source only, load only or both by the source and the load. |
II.REFORMULATING OF POWER COMPONENTS DEFINITIONS IN WAVELET DOMAIN |
| In nonsinusoidal situations, power components definitions are based on a frequency domain approach using Fourier Transform (FT). The frequency domain approach can provide amplitude–frequency spectrum information loosing time related information. To overcome these limitations time frequency based approaches are developed to define power quantities and quality factors through the use of wavelet transform. The rms values of voltage and current are: |
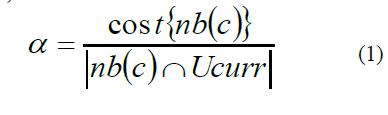 |
| The rms value of the voltage (Vj0) and current (Ij0) of the lowest frequency band j0 are also called approximated voltage (Vapp) and approximated current (Iapp), respectively. The sets of rms values of voltage (Vj) and current (Ij) of each frequency band or wavelet-level higher than or equal to the scaling level j0 are called detailed voltage (Vdet) and detailed current (Idet), respectively. |
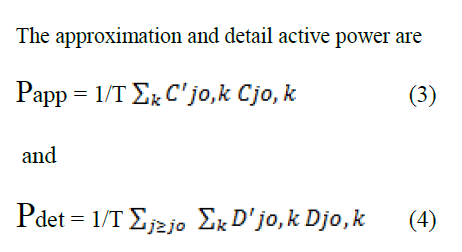 |
| Here C’jo,k and Cjo,k are the voltage and current discrete wavelet coefficients at the scaling level j0 and k while D’jo,k and Djo,k are the voltage and current discrete wavelet coefficients at any other level j than the scaling level j0 and sample k. |
 |
III.IDENTIFICATION OF HARMONIC CONTENT |
 |
 |
 |
| Consider the Fig 1,the first fig is the original harmonic signal. Next the signal is decomposed into detail signal and approximate signal with the help of wavelet transform. Again the detail signal is decomposed into 6 levels. By decomposing signal into 6 levels ,the exact harmonic content was identified. The decomposed signals will also give the accurate information about time and frequency information of harmonic content. The main difference between decomposing detail and approximate signal is getting information about low and high frequency harmonics. The decomposed detail signal will give information about low frequency harmonics. The decomposed approximate signal will give information about high frequency harmonics. |
VI.DETECTION OF HARMONIC SOURCE |
| The direction of harmonic power flow with respect to the direction of the flow of fundamental frequency power has been used to identify the location of the harmonic source in the literature. The total harmonic power method for identifying the source of harmonic pollution in radial system is presented in [15].The total harmonic power at a certain node is used for the indication of existence of a polluting load. If the total harmonic power is positive at a certain node in the system then a harmonic source exists upstream and the harmonic power is received from the source side. If the total harmonic power is negative then a harmonic source exists downstream of the node and the harmonic power is received from the load side. The signs of individual harmonic powers have been used to identify the dominant source of harmonic pollution at each harmonic order. The effect of nonsinusoidal supply has not been considered here. A single point strategy for the detection of harmonic sources developed from IEEE Standard 1459-2000 approach is presented in [10]. |
| Wavelet transform based analysis has been used to extract harmonic information contained in a power system voltage/ current pollution in radial and nonradial systems. The signs of total and individual harmonic powers can provide detailed information about the harmonic pollution [15]. |
| Fig. 6 shows a radial power system network with five loads. This network is used to perform experimentation for the identification of a feature signature of harmonic source and also to validate the proposed method in a later section. The fundamental frequency internal impedance of the voltage source ZS is considered to be 1 + j 6.28 Ω and the line impedance is 1 + j 12.56 Ω. The fundamental frequency impedance of each load viz. Z1, Z2, Z3 and Z4 is 100 + j 62.8 Ω when all the loads are linear and thyrsitor controlled bridge rectifier is connected with each load to make it a nonlinear load. The nonlinearity of the load has been varied by varying the firing angles of the thyristor. EMTP simulation package has been used to capture the instantaneous voltage and current waveforms at the different nodes in the system. The voltages and currents are processed and analyzed using discrete wavelet transform in MATLAB. |
 |
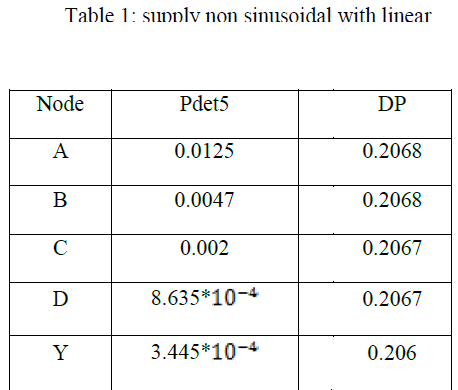
CASE – I: supply non sinusoidal with linear loads |
| The supply voltage is assumed to be nonlinear as V = 230 sin 314t + 60 sin 942t + 15 sin 1570t + 4 sin 2198t. The loads are linear. The detail power analysis results are given in Table 1. Since the supply is the source for the harmonics and loads are linear, all detail powers are found to be positive i.e., direction of flowing is same as the fundamental frequency power. |
 |
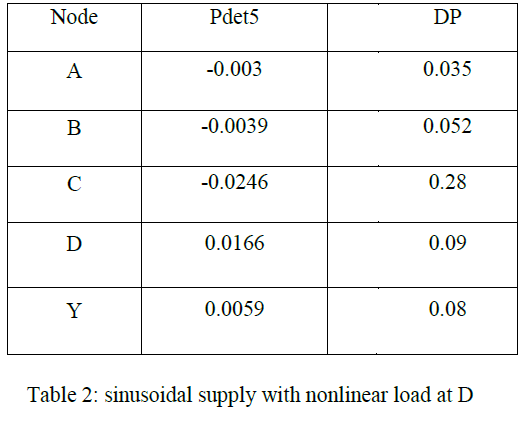
CASE – II (a): sinusoidal supply, load at node C is nonlinear, all other loads are linear |
| Here the supply is assumed to be pure sinusoidal with V=230 sin 314t .The nonlinear load at node C. Detail power and details pollution obtained from wavelet analysis are shown in Table 2. The detail powers Pdet5 are all negative up to point C and beyond point C all are positive. |
| At node C, DP is high i.e., amount of harmonic pollution is high. |
 |
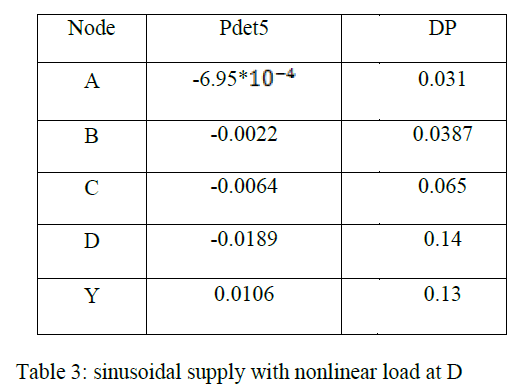
CASE – II (b): sinusoidal supply, load at node D is nonlinear, all other loads are linear |
| In this case also the supply is linear, but the load at D is made nonlinear. The detail power analysis results are given in Table 3. It is seen that detail powers at level 5 is negative up to node D where the nonlinear load is connected, and detail pollution at node D is high. |
 |
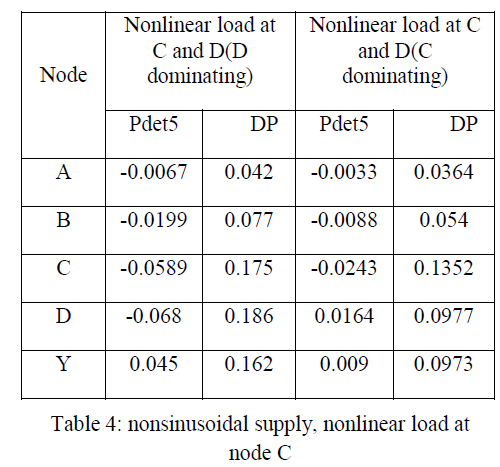 |
CASE – III: nonsinusoidal supply, nonlinear load at node C |
| Here supply is nonsinusoidal and the load at C is nonlinear. The detail power analysis is shown in Table 4. The sign of the detail power Pdet1 at the node adjacent to the supply is positive indicating location of nonsinusoidal source in the upstream side. At nodes B and C the sign of Pdet5 is negative indicating location of nonlinear load at node C. As the nonlinear load is located at C, nodes D and Y receive harmonic power from the upstream side as indicated by the positive sign of Pde5 at D and Y. |
CASE – IV: sinusoidal supply with two adjacent nonlinear loads |
| In this case we consider the method of detection of harmonic source when more than one nonlinear load is present. We consider sinusoidal supply and two adjacent nonlinear loads at C and D as shown in Table 5.Nonlinear load is present in C and D. As DP is higher at D than at C hence detail power Pdet5 is negative up to point D indicating that the nonlinear load at D is acting as the dominant source of harmonic pollution. The magnitude of detail power Pdet5 is maximum at D and decreases according to the decreasing order of DP. When DP at C is higher than DP at D then positive detail power at D indicates that the nonlinear load is located upstream with respect to point D. |
 |
VI.CONCLUSION |
| In this paper a new method based on active detail power measurement has been proposed for the identification of the of harmonics and harmonic pollution source in power systems. This method is based on the comparison of signs of detail powers at lower level of decomposition. The location of the nonlinear load when a single nonlinear load is present and also location of the dominant source of harmonic pollution when more than one nonlinear load are present can be detected by observing the signs of the detail powers. The presence of harmonics in the source can be detected from the magnitude of details power at the highest level of decomposition.Simulation results show that the proposed method can give useful indications about the location of the dominant harmonic source, upstream or downstream the point of measurement. |
References |
|