e-ISSN: 2347-7857 p-ISSN: 2347-7849
e-ISSN: 2347-7857 p-ISSN: 2347-7849
Maria Durisova*
Institute of Experimental Pharmacology, Slovak Academy of Sciences, Slovak Republic
Received date: 24/11/2015 Accepted date: 16/02/2016 Published date: 22/02/2016
Visit for more related articles at Research & Reviews: Journal of Pharmaceutics and Nanotechnology
The main goal of the current study was to present a further example which showed a successful use of an advanced mathematical modeling method based on the theory of dynamic systems in mathematical modeling in pharmacokinetics. An additional goal was to motivate researchers working in field of pharmacokinetics to use of an alternative modeling method to those modeling methods commonly used in pharmacokinetic studies. The current study is a companion piece to an earlier study (Antal et al. 1983) in volunteers published in the December issue of Journal of Pharmacokinetics and Biopharmaceutics. In the study cited here, an investigation of pharmacokinetics of methypprednisolone orally administered to fourteen healthy adult male volunteers was described. The mathematical modeling method used in the current study is universal, comprehensive, and flexible. Therefore, it can be used to developed mathematical models not only in pharmacokinetics but also in many other scientific fields.
Methylprednisolone, Oral administration, Mathematical model.
Methylprednisolone (MLP) is a synthetic glucocorticoid steroid which is well known for its anti-inflammatory activity in disorders of many organ systems [1]. It is well suited for use in situations which require rapid achievement of drug concentrations in blood. In the study, pharmacokinetics of MLP was investigated in fourteen adult male volunteers after the oral administration of MLP [1].
The main goal of the current study was to present a further example which showed a successful use of an advanced mathematical modeling method based on the theory of dynamic systems in mathematical modeling in pharmacokinetics [2-13]. An additional goal was to motivate researchers in pharmacokinetics to use of an alternative modeling method to those modeling methods commonly used in pharmacokinetic studies. Previous examples presenting an advantageous use of the modeling method used in the current study can be found in full-text articles which could be downloaded free of cost from the following Web pages: http://www.uef.sav.sk/durisova.htm and http://www.uef.sav.sk/advanced.htm.
The data published in the study were employed. For modeling purposes, an advanced mathematical modeling method based on the theory of dynamic systems was used; see e.g., the studies cited above [1]. Mathematical modeling was performed in the following steps:
The development of a mathematical model of each pharmacokinetic dynamic system H was based on the following simplifying assumptions: a) initial conditions of each pharmacokinetic dynamic system H were zero; b) the pharmacokinetic processes occurring in the body after the oral MLP administration; were both linear and time-invariant, c) concentrations of MLP were the same throughout all subsystems of the pharmacokinetic dynamic systems H (where subsystems were integral parts of the whole pharmacokinetic dynamic systems H); d) no barriers to the distribution and/or elimination of MLP existed. The modeling method used in the current study can be described as follows:
In the first step, a pharmacokinetic dynamic system, here denoted as H, was defined for each volunteer by relating the Laplace transform of the plasma concentration time profile of MLP, here denoted as C(s), and the Laplace transform of the MLP oral input to the body, here denoted as I(s).
In the second step, the pharmacokinetic dynamic systems H, were used to mathematically represent static and dynamic aspects of the pharmacokinetic behavior of MLP in the body [3-16].
In the third step, the transfer function, here denoted as H(s), of the pharmacokinetic dynamic system H (see Eq. (1)) was derived for each volunteer by relating Laplace transform of the mathematical representation of the plasma concentration-versustime profile of MLP, here denoted as C(s), and the Laplace transform of the mathematical representation of the oral administration of MLP, here denoted as I(s), (the lower case letter “s” denotes the complex Laplace variable), see e.g., the following studies [3-13] and references therein and the following equation:
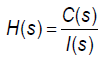 (1)
(1)
Thereafter, the pharmacokinetic dynamic system H of each volunteer was described with transfer function here denoted as H(s) [3-13]. The transfer function H(s) of the dynamic system H of each volunteer was derived and by relating the Laplace transform of the plasma concentration time profile of MLP, here denoted as C(s), and the Laplace transform of the MLP input to the body, here denoted as I(s) (see Eq. (1)).
For modeling purposes, the software named CTDB and the transfer function model HM(s), described by the following equation were used [8]:
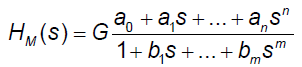 (2)
(2)
On the right-hand-side of Eq. (2) is the Pade approximant to the model transfer function HM(s),G is an estimator of the model parameter called the gain of the dynamic system H, a1, Λ, an, b1, Λ, bm are the additional model parameters, n is the highest degree of the nominator polynomial, and m is the highest degree of the denominator polynomial, where n<m [3-13].
In the fourth step, the transfer function H(s) was converted to equivalent frequency response function, here denoted as F(iωj).
In the fifth step, the non-iterative method published previously was used to determine a mathematical model of the frequency response function FM (iωj) of each volunteer and point estimates of parameters of the model frequency response function FM (iωj) in the complex domain [17]. The model of the frequency response function FM (iωj) used in the current study is described by the following equation:
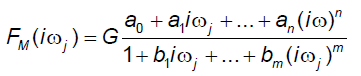 (3)
(3)
Analogously as in Eq. (2), n is the highest degree of the numerator polynomial of the model frequency response function FM (iωj), m is the highest degree of the denominator polynomial of the model frequency response function FM (iωj), n ≤ m, i is the imaginary unit, and ω is the angular frequency in Eq. (3). In the fifth step, each the model frequency response function FM (iωj) was refined using the Monte-Carlo and the Gauss-Newton method in the time domain.
In the sixth step, the Akaike information criterion was applied to discriminate among models of frequency response functions FM (iωj) of different complexity and to select the best model of the frequency response function FM (iωj) with the minimum value of the Akaike information criterion among all mathematical models developed [18]. In the final step of the method, 95% confidence intervals for parameters of the final models FM (iωj) were determined.
After the development of mathematical models of the pharmacokinetic dynamic systems H, the following primary pharmacokinetic variables were determined: The time of occurrence of the maximum observed plasma concentration of MLP, here denoted as tmax, the maximum observed plasma concentration of MLP, here denoted as Cmax, the elimination half-time of MLP, here denoted as t1/2 the area under the plasma concentration versus time profile of MLP from time zero to infinity, here denoted as, AUC0-∞ and total body clearance of MLP, here denoted as CI.
The transfer function model HM(s) and the frequency response function model FM (iωj) have been implemented in the computer program CTDB [8]. A demo version of the computer program CTDB is available at: http://www.uef.sav.sk/advanced.htm.
The best-fit third-order model of FM (iωj) selected with the Akaike information criterion is described by Eq. (4):
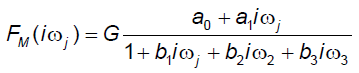 (4)
(4)
This model provided an adequate fit to the MLP concentration data in all volunteers investigated in the previous and the current study [1]. Estimates of the model parameters a0, a1, b1, b2, b3 are listed in Table 1. Model-based estimates of primary pharmacokinetic variables are given in Table 2. Model predicted blood concentrations of methylprednisolone are given in Table 3.
| Model parameters | Estimates of model parameters |
(95% CI) |
|---|---|---|
| G(h.l-1) | 0.007 | 0.006 to 0.012 |
| a0(-) | 0.99 | 0.81 to 1.02 |
| a1(min) | 59.15 | 48.12 to 62.38 |
| b1(min) | 461.88 | 460.73 ton472.02 |
| b2(min2) | 6033.61 | 6028.59 to 6040.33 |
| b3(min3) | 3678275.74 | 3678271.05 to 3678280.33 |
Table 1: Parameters of the third-order model of the dynamic system describing the pharmacokinetic behavior of orally administered methylprednisolone to Volunteer No.1.
| Pharmacokinetic variable | Estimates |
|---|---|
| The time of the maximum observed concentration of methypprednisolone tmax(min) |
2.12 ± 0.61* |
| The maximum observed concentration of MLP methypprednisolone Cmax(ng/ml) | 293,1± 18.52 |
| the plasma elimination half-time of MLP t1/2(hod) |
2.4 ± 0.41 |
| Renal clearance of methyprednisolone/F (L/hr) | 12.2 ± 15.25 |
| Mean absorption time of methyprednisolone (hr) | 0.84 ± 0.1 |
| Men residence time of methyprednisolone CI (ml.min-1) from plasma |
3.67 ± 5.06 |
| *standard deviation | |
Table 2: Pharmacokinetic variables of orally administered methylprednisolone to Volunteer No.1.
| Time (h) | Observed concentration of methylprednisolone (ng/ml) |
Model predicted concentration of methylprednisolone (ng/ml) |
|---|---|---|
| 0 | 0 | 0 |
| 0,5 | 47.4 | 48 |
| 1.0 | 185 | 185 |
| 2 | 293 | 293 |
| 4 | 254 | 254 |
| 6 | 158 | 158 |
| 9 | 76.9 | 76.9 |
| 12 | 130 | 130 |
Table 3: Observed and model predicted blood concentrations of methylprednisolone in Volunteer No.1.
Volunteer No.1 was arbitrarily chosen from fourteen volunteers investigated in the previous study and in the current study, to illustrate the results obtained [1]. Figure 1 showed the observed plasma concentration versus time profile of MLP and the description of the observed profile with the developed model of the pharmacokinetic dynamic system H, Analogous results also hold for all volunteers investigated in the previous and the current study [1].
Figure 1. Observed plasma concentration versus time profile of methylprednisolone and the description of the observed profile with the model of the dynamic system of Volunteer No.1 which mathematically represented the static and dynamic aspects of the pharmacokinetic behavior of methylprednisolone in Volunteer No. 1.
The pharmacokinetic dynamic system used in the current study is a mathematical object, without any physiological relevance. It was used to model static and dynamic aspects of the pharmacokinetic behavior of MLP in the healthy male Volunteer No.1 investigated in the previous and current study [1,14-16]. The method used in the current study has been described in detail in the previous studies [3-13].
As in previous studies, authored or co-authored by the author of the current study, the development of mathematical models of the dynamic systems H, was based on the known inputs and outputs of the dynamic systems H. In general, if a dynamic system is modeled using the transfer function models HM(s), as it was the case in the current study, then the accuracy of the model depends on the degrees of the polynomials of the transfer function models HM(s) used to fit the data, see e.g. the following studies [3-14].
The parameter gain is also called gain coefficient, or gain factor. Generally, the parameter gain is defined as a relationship between the magnitudes of an output of the dynamic system to a magnitude of an input to the dynamic system in steady state. Or in other words, the parameter gain of a dynamic system is a proportional value that shows the relationship between the magnitudes of an output to a magnitude of an input of a dynamic system in steady state.
The pharmacokinetic meaning of the parameter gain depends on the nature of the dynamic system; see e.g., studies available at: http://www.uef.sav.sk/advanced.htm.
The non-iterative method published in the study and used in the current study is capable of providing quick identification of an optimal structure of a model frequency response [17]. This is a great advantage of this method, because this significantly speeds up the development of frequency response models.
The reason for conversion of HM(s) to FM (iωj) can be explained as follows: the variable: “s” in HM(s) is a complex Laplace variable (see Eq. (2)), while the angular frequency ω (see Eq. (4)) is a real variable that is suitable for modeling purposes.The linear mathematical models developed in the current study sufficiently approximated static and dynamic aspects of the pharmacokinetic behaviour of MLP in the volunteers investigated in the previous and the current study [1].
The current study repeatedly showed that mathematical and computational tools from system engineering can be successfully used in mathematical modeling in pharmacokinetics. Frequency response functions are complex functions, therefore modeling is performed in the complex domain. The modeling methods used to develop model frequency response functions are computationally intensive, and modeling require at least partial knowledge of the theory of dynamic system, and an abstract way of thinking about the dynamic system under study.
The principal difference between traditional pharmacokinetic modeling methods and modeling methods that use of mathematical and computational tools from the theory of dynamic systems, is as follows: the former methods are based on modeling plasma (or blood) concentration versus time profiles of drugs, however the latter methods are based on modeling relationships between a mathematically represented drug administration and a mathematically represented resulting plasma (or blood) concentration-time profile of the drug administered. See e.g., the studies and the explanatory example available at http:// www.uef.sav.sk/advanced.htm.
The computational and modeling methods that use computational and modeling tools from the theory of dynamic systems can be used for example for adjustment of drug (or a substance) administration aimed at achieving and then maintaining required drug (or a substance) concentration–time profiles in patients see e.g. the following study [6].The methods considered here can be used for safe and cost-effective individualization of drug (or a substance) dosing e.g. by computer-controlled infusion pumps. This is very important for example for administration of a clotting factor to hemophilia patients, as exemplified in the simulation study [6].
The advantages of the model and modeling method used in the current study are evident here: The models developed and used overcome one of the well-known limitations of compartmental models: For the development and use of the models considered here, an assumption of well-mixed spaces in the body is not necessary. The basic structure of the models developed and used is and broadly applicable to mathematical modeling different dynamic systems in the field of pharmacokinetics and in many other scientific as well as practical fields. From a point of view of pharmacokinetic community, an advantage of the models developed using computational tools from the theory of dynamic systems is that the models considered here emphasize dynamical aspects of the pharmacokinetic behavior of a drug in a human and/or an animal body. The method used in the current study can be easily generalized. Therefore, there is no problem to use the method considered here in several scientific and practical fields. Transfer functions of dynamic systems are not unknown in pharmacokinetics; see e.g. the following studies [18-23].
The models developed and used in the current study successfully described the pharmacokinetic behavior of MLP after the oral administration to healthy male adult volunteers. The modeling method used is universal, comprehensive and flexible and thus it can be applied to a broad range of dynamic systems in the field of pharmacokinetics and in many other fields. The current study repeatedly presented an attempt to visualize a successful use of mathematical and computational tools from the theory of dynamic systems in pharmacokinetic modeling. For the previous attempts with the use of the modeling method used in the current study please visit http://www.uef.sav.sk/advanced.htm. The current study repeatedly showed that an integration of pharmacokinetic and bioengineering approaches is a good and efficient way to study processes in pharmacokinetics, because such integration combines mathematical rigor with biological insight.
There is no conflict of interest.
The author is a research worker affiliated with the Institute of Experimental Pharmacology and Toxicology, the Department of Pharmacology of Inflammation Slovak, Academy of Sciences Bratislava, Slovak Republic. Her main research interest is to some extant outside her education, because it involves investigations of various dynamic systems in pharmacokinetics, using mathematical models. However, during her work in pharmacokinetics, she has successfully utilized her good knowledge of mathematics, based on her engineering education, what is fundamental in order to develop accurate mathematical models in pharmacokinetics. For more information about the modeling methods used by the author and their use in pharmacokinetic studies, please visit the author’s web page at: www.uef.sav.sk/durisova.htm.
The author worked as a researcher and contractor in the 6FP-Project “Network of Excellence: Biosimulation - A New Tool in Drug Development, contract No. LSHB CT-2004-005137“and in the 7FP-Project “Network of Excellence: Virtual Physiological Human”. Both projects were established by the European Commission. Author worked also in several previous COST program actions. This work of the author in several international projects led to the preparation of the current study.
At present, the author precipitates in the Action BM1204 of the COST program entitled: An integrated European platform for pancreas cancer research: from basic science to clinical and public health interventions for a rare disease.
The author gratefully acknowledges the financial support from the Slovak Academy of Sciences in Bratislava, Slovak Republic.
This study is dedicated to the memory of the late Professor Luc Balant who passed away unexpectedly in December 2013. Internationally, Professor Luc Balant was widely known for his work in the COST Domain Committee for Biomedicine and Molecular Biosciences and in the COST Action B15: “Modeling During Drug Development”.
The motto of this study is: “The undergoing physical laws necessary for the mathematical theory of a large part of physics and of the whole chemistry are thus completely known, and difficulty is only that the exact application of these laws lead to equations much more complicated to be soluble”. (One of the outstanding theoretical physicists P. A. M. Dirac (1902-1984)).