ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Binod Prasad Dhakal Associate professor, Central Department of Mathematics (Education), Tribhuvan University, Nepal |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this In this paper a new estimate on degree of approximation of conjugate function ~ f conjugate to a function f belonging to Lipï¡ class has been determined by (E,1) (C,1) summability of conjugate series of a Fourier series..
Keywords |
| Degree of approximation, (E,1) (C,1) Summability, Fourier series, Lipï¡ class. |
INTRODUCTION |
A function 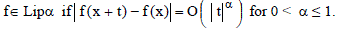 |
| The degree of approximation En(f) of a function f: R→ R by a trigonometric polynomial tn of degree n is defined by (Zygmund (1959)) |
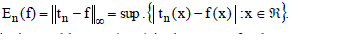 |
| Let f be 2ï° periodic, integrable over (-ï°,ï°) in the sense of Lebesgue and belonging Lipï¡ class, then its Fourier series is given by |
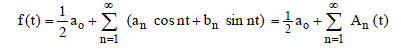 and its conjugate series is and its conjugate series is |
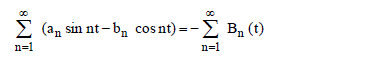 (1) (1) |
Let 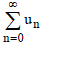 be the infinite series whose nth partial sum is given by be the infinite series whose nth partial sum is given by 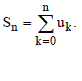 |
The Cesàro means (C, 1) of sequence {Sn} is 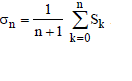 |
If 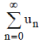 be the infinite series whose nth partial sum is given by be the infinite series whose nth partial sum is given by 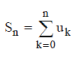 |
The Cesàro means (C, 1) of sequence {Sn} is 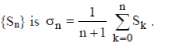 |
If 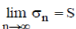 then sequence {Sn} or the infinite series then sequence {Sn} or the infinite series 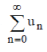 is said to be summable by Cesàro means (C,1) to S. (Hardy (1913), p.96) is said to be summable by Cesàro means (C,1) to S. (Hardy (1913), p.96) |
The Euler means (E, 1) of sequence {Sn} is 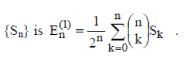 |
If 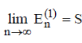 then sequence {Sn} or infinite series then sequence {Sn} or infinite series 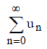 is said to be summable by Euler means method (E, 1) to S. is said to be summable by Euler means method (E, 1) to S. |
The (E, 1) (C, 1) transformation of {Sn}, denoted by 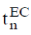 , is given by , is given by |
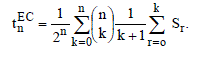 |
If 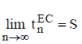 then sequence {Sn} or infinite series then sequence {Sn} or infinite series 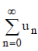 is said to be summable by (E, 1) (C, 1) means method to S. is said to be summable by (E, 1) (C, 1) means method to S. |
| If a function f is Lebesgue integrable then |
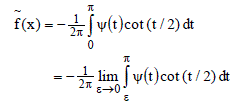 |
| exist for all x (Zygmund (1959), p. 131). We use following notations. |
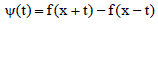 |
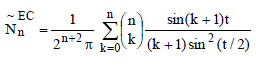 |
II. MAIN THEOREM |
There are several results, for example, Alexits (1965), Chandra (1975), Sahney & Goel (1973) and Alexits & Leindler (1965) for the degree of approximation of functions f ïÂÂLipï¡, but most of these results are not satisfied for n= 0, 1 or α = 1.Therefore, this deficiency has motivated to investigate degree of approximation of functions belonging to Lip α considering cases 0< α <1 and α = 1 separately. Considering theses specific cases separately, we have obtained better and sharper estimate of 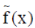 ,~ conjugate of Lip α than all previously known results as follows, ,~ conjugate of Lip α than all previously known results as follows, |
Theorem: If f: R → R is 2π periodic, Lebesgue integrable function in (-π,π) and belonging to Lip α, 0< α ≤1, then the degree of approximation of 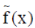 the conjugate of a function fïÂÂLip α by (E,1) (C,1) means the conjugate of a function fïÂÂLip α by (E,1) (C,1) means |
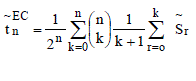 of the conjugate series of the Fourier series (1) satisfies, for n=0, 1, 2…, of the conjugate series of the Fourier series (1) satisfies, for n=0, 1, 2…, |
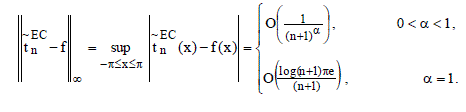 |
III. LEMMAS |
| We need the following lemmas for the proof of the theorem. |
Lemma 1: 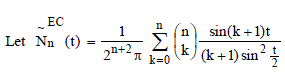 then then |
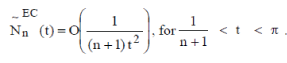 |
Proof: 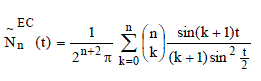 |
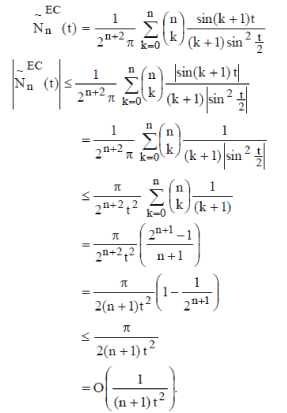 (3) (3) |
IV. PROOF OF THE THEOREM |
The nth partial sum 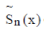 of conjugate series (1) is given by of conjugate series (1) is given by |
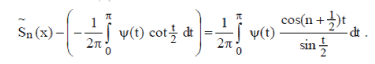 |
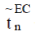 transform of the transform of the 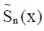 is given by is given by |
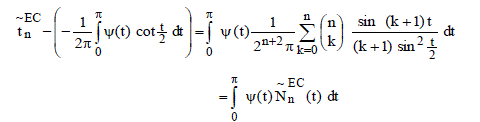 |
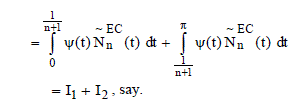 (4) (4) |
Using Lemma 1 and the fact that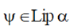 , we have, , we have, |
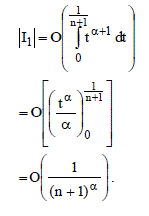 (5) (5) |
| Now, using Lemma 2, we have |
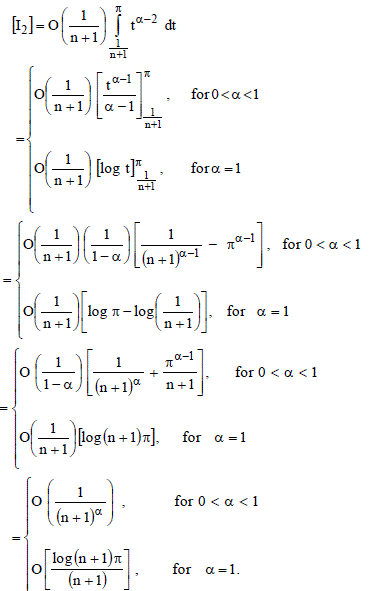 (6) (6) |
| Collecting (.4), (5), (6); we have |
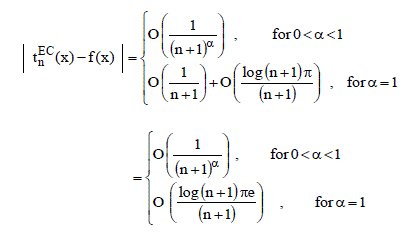 |
| or |
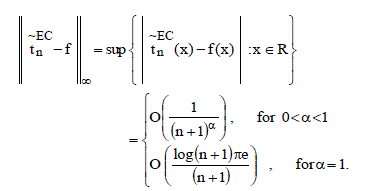 |
| This completes the proof of theorem. |
V. CONCLUSION |
| In this paper a new theorem on degree of approximation of conjugate function f conjugate to a function f belonging to Lipα class has been established by (E,1) (C,1) summability of conjugate series of a Fourier series. |
References |
|