ISSN:2321-6212
ISSN:2321-6212
Li LB1,2*, Li GL1, Kan Y2, Lu XM2 and Zhu JS2
1School of Physics and Engineering, Henan University of Science and Technology, Luoyang, China
2National Lab of Solid State Microstructures, Nanjing University, Nanjing, China
Received Date: 13/06/2017; Accepted Date: 11/07/2017; Published Date: 20/07/2017
DOI: 10.4172/2321-6212.1000178
Visit for more related articles at Research & Reviews: Journal of Material Sciences
The decay properties of reversed domains fabricated by scanning probe microscopy fixed-point poling in LiNbO3 single crystals are simulated by a modified dynamic Ginzburg–Landau equation based on a simple model. The depolarization field is equivalently acted by the coercive field of ferroelectrics. The penetrated domain with a small coercive field is stable and has a long lifetime. The non-penetrated domain with maximum coercive field may ultimately experience a metastable state and disappears. Our theoretical results well agree with known experiments. We predict that the non-penetrated domain lifetime decreases with increased temperature.
LiNbO3, Reversed domain, Decay, Ginzburg–Landau equation, Coercive field
Artificially ordered domain structures could be used in electro-optic modulators, and the domain switching property under external field is useful for data storage. The key for increasing the degree of miniaturization and integration density of ferroelectricbased devices is the formation of stable domains with submicron and nanometer lateral dimensions. LiNbO3 single crystal is a ferroelectric with an ABO3 structure and high spontaneous polarization (PS ≈ 0.75 C/m2 at room temperature) [1-3]. It occurs at the second-order phase transition from spatial group R3c (C3v6) to 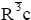 (D3d6) at a high Curie temperature (TC=1484 K) [1,3-6]. Progress in the applications of scanning probe microscopy (SPM) in fabricating and exploring the micro- to nanoscale domain structures in LiNbO3 has revealed new opportunities for the development of short-wave output and high-density storage [7-10].
(D3d6) at a high Curie temperature (TC=1484 K) [1,3-6]. Progress in the applications of scanning probe microscopy (SPM) in fabricating and exploring the micro- to nanoscale domain structures in LiNbO3 has revealed new opportunities for the development of short-wave output and high-density storage [7-10].
Bulk LiNbO3 crystals were poled by various voltage pulses at ïìÃÂxed points, and the decay process of the fabricated domains after poling was investigated by Kan et al. using SPM [9]. They found the following rules: (1) Reversed domains with an initial radius r larger than the critical initial radius rC existed beyond 5 days; rC corresponded to the point at which the domain just penetrated the crystal. (2) rC is related to the thickness of the crystals H, that is, rC =107 × H0.363 . (3) Domains with an initial radius, RC<r<rC, experienced a metastable state before completely disappearing. (4) Domains smaller than the initial radius RC switched back rapidly. (5) The dependence of domain life time on the initial radius obeyed an exponential law.
Kan et al. [9] used the Molotskii’s theory [11-14] to explain their experimental results qualitatively. The quantitative explanation, especially on the dependence of the domain lifetime on temperature, is still limited. In this paper, a simple model is proposed to investigate the decay properties of the reversed domains fabricated by SPM–fixed-points poling in LiNbO3 single crystals. A modified dynamic Ginzburg–Landau equation is used to simulate the domain evolution. The results agree with the experimental results by Kan et al. [9].
Theoretical Development
As shown in Figure 1, the reversed domain is surrounded by a cylinder LiNbO3 crystal with radius R (an adjustable parameter) and length H (the thickness of the crystal). The domain is assumed to have a half ellipsoid shape with semi-axes parallel (l) and perpendicular (r) to the spontaneous polarization direction [11]. After poling, the domains decay and reach a ïìÃÂnal stable state under the free energy minimum condition [12]. Following Kan [9] and Molotskii [13,14], an invariant shape was assumed to exist, i.e.,
r = Cl1/3 (1)
Obviously, positive bond charges gather on the domain wall. The charges contributed by the reversed domain (the white region) are repulsed by the charges contributed by the unrevised region (the grey region), which induce the reversed domain decay or the growth of the unrevised region. We define polarization as to describe the growth of the unrevised region or the decay of the reversed domain. The reversed domain disappears when r=0 or P=1.
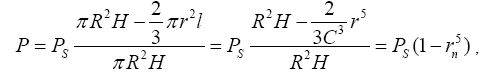 (2)
(2)
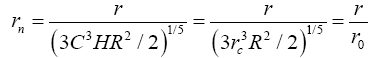 (3)
(3)
Following the dynamical model that describes the hysteresis in ferroelectric ceramics presented by Guyomar et al. [15,16], the evolution of P satisfies:
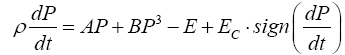
Where ρ is the electrical resistivity of LiNbO3 single crystal and dependent on temperature T with the Arrhenius relation [17].
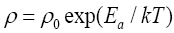 (5)
(5)
Where ρ0 is the pre-exponential factor, k is the Boltzmann constant, and Ea is the activation energy. ρ is considered a damping factor in other cases [18-20]. E is the external electric field and is zero for the reversed domain decay case discussed. EC is the coercive field of ferroelectrics and dependent on the temperature and reversed domain length. Here, it acts equivalently to the Coulomb repulse of the bond charge on the domain wall, similar to the depolarization field in Wang’s model [17]. A and B are the coefficients of the Ginzburg–Landau–Devonshire free energy per unit volume of the LiNbO3 single crystals [3],
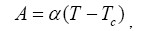
B is independent on the temperature. With E=0, let
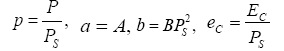 (7)
(7)
Eq. (4) becomes
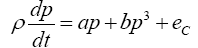 (8)
(8)
and Eq. (2) becomes
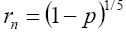 (9)
(9)
Consider the steady state of eqn. (8),
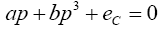
Let
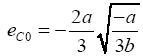
Three real roots can be derived from eqn. (10) when ec < ec0, two real roots when ec= ec0 , and one real root when ec > ec0. If certain small time-dependent perturbations are imposed on the system within the framework of a linear analysis [21], the perturbed state is given by:
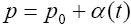
With 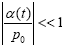 . p0 is one solution for eqn. (6). Substituting eqn. (9) into the time-dependent kinetic eqn. (10) then yields the following relation:
. p0 is one solution for eqn. (6). Substituting eqn. (9) into the time-dependent kinetic eqn. (10) then yields the following relation:
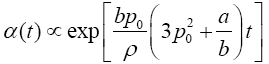
p0 is the stable solution for eqn. (10) when 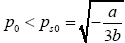 . It is a non-stable solution when p0 > ps0 and critical stable when p0=ps0.
. It is a non-stable solution when p0 > ps0 and critical stable when p0=ps0.
Based on eqns. (5-11) and the parameters listed in Table 1, the decay properties of the reversed domains in LiNbO3 single crystals are calculated and discussed as follows:
Table 1. Parameters used in this work [1-3,20]
| TC (K) | PS (C/m2) | α(m/F) | b (m/F) | rC(nm) | Ea/k (K) | H(nm) |
|---|---|---|---|---|---|---|
| 1484 | 0.75 | 1.588 × 106 | 1.883 × 109 | 540 | 1623 | 88000 |
1. The Coercive Field and Stability of the Penetrated Domain
For the penetrated domain shown in Figure 1b, the Coulomb repulse of the bond charge on the domain wall is weaker than that of the non-penetrated domain shown in Figure 1a. The bigger the initial domain radius is, the more part is penetrated and the smaller is the coercive field ec. The dependence of the normalized polarization (p > 0) on eC at room temperature is calculated by eqn. (10) and shown in Figure 2a. A stable solution p01 for one eC<eC0 was obtained. The time dependence of the normalized radius (rn) for various initial values at room temperature are calculated and shown in Figure 2b. The theoretical results are qualitatively consistent with the experimental results [9].
2. Time Evolvement of the Non-Penetrated Domain
For the non-penetrated domain shown in Figure 1a, ec= ec0 . The solution of eqn. (10), p=ps0, is critical stable. With ρ0 = 1.5×109 Ω⋅m, the time dependence of the normalized radius (rn) for various initial values are obtained and shown in Figure 3a. The reversed domains disappear when rn = 0. The reversed domains with an initial normalized radius larger than 0.86 exhibit a metastable state. The result agrees with Molotskii’s conclusion obtained by dynamic theory [14]. The reversed domain exits a few seconds when its initial normalized radius is smaller than 0.6. The domain with intermediate radius keeps the period of time. The decay characteristic of the reversed domain originates from the nonlinear property of the LiNbO3 crystals and is independent on the thickness. With r0=572 nm (R=510 nm), the time dependence of the normalized radius at room temperature are plotted, as shown in Figure 3b. The theoretical results well agree with the experimental results by Kan [9].
3. Dependence of the Domain Lifetime on the Initial Domain Radius and Temperature for Non-Penetrated Domain
With ρ0 = 1.5×109 Ω⋅m and r0=572 nm (R=510 nm), the dependence of the domain lifetime on the initial domain radius for H=88 μm is plotted, as shown in Figure 4a. The parameters a and eC in eqn. (8) are temperature dependent; hence, the domain lifetime on the temperature can be predicted for initial domain radius 500 nm, as shown in Figure 4b. The domain lifetime decreases rapidly as the temperature increases. Obviously, thermal motion intensifies the domain decay. On one hand, increased temperature gives rise to the high nonlinearity in eqn. (8). On the other hand, increased temperature reduces the electrical resistivity.
A modified dynamic Ginzburg–Landau equation is used to simulate the decay properties of the reversed domains fabricated by SPM–fixed-points poling in LiNbO3 single crystals. The penetrated domain has a very long lifetime. The domain lifetime increases as the initial domain radius increases for the non-penetrated domain. The theoretical results well explain the experimental results. The Coulomb repulse of the bond charge on the domain wall may be equivalent to the coercive field of ferroelectrics. The domain lifetime decreases as the temperature increases.