International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Trivariate Poisson Processes for Modeling the Stage Dependent Cancer Cell Growth

P. Tirupathi Rao 1, B.N. Naveen Kumar 2, J.Jayabharathiraj 1
  1. Dept. of Statistics, Pondicherry University, Puducherry-605014, India
  2. Dept. of Statistics, S.V. University, Tirupati - 517 502, A.P., India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Studying the cancer cell growth through trivariate Poisson processes is the core objective of this paper. The parameters on growth, transitions and loss processes at different independent and inter dependent stages are considered for stochastic modeling of cancer growth in a human body. Formulation of joint probability functions and deriving statistical measures were carried out through differential equations. Model behaviour was analyzed with numerical data.

Keywords
Trivariate Poisson Processes, Stochastic Modeling, Differential Equations and state dependent Cancer Growth

INTRODUCTION
Cancer is due to the failure of regulating mechanism on cell division, leads to continuous proliferation and growth of cells. The deviation in the growth and division programming of normal cells will initiate the cancer formations and its invasion. This may be due to several unexplained reasons. Cancer cells have different DNA compared to normal/healthy cells. The division of normal cell is in standard pace and it is governed by DNA, proto-oncogenes, tumor suppressor gene, repair gene, etc. The state of repair gene fails/turned off/unable to fix the problem in the cells will generate rapid cell division in the organ. These factors will provoke rapid and uncontrolled cell division is a prime characteristic of cancer.
Assessment of cancer status through mathematical modeling is a fit in approach of understanding its growth. It has attracted good attention of researchers in mathematical biology. Counting the number of cancer causing cells in the tumor of different categories through manual methods is hypothetical and beyond experimentations. The numbers of cells in different categories of human body are variables and influenced by several uncertainties. Hence, there is a need in understanding the cancer growth with stochastic modeling of biological issues.
The pioneering work on quantification of cancer growth was done by Mayneord [1]. Kendall [2] has given a breakthrough in modeling a cell growth using the uni-variate birth and death process. Neyman et al. [3] have used linear birth and death process to describe the tumor growth as density dependent. First order partial differential equations have been used by Macro et al. [4], Murray [5] and Dewanji et al. [6] to develop mathematical models for studying the cancer growth. The limitations on the deterministic assumptions of biological issues in modeling the cancer growth leads to development of many models based on stochastic assumptions by Neymann [7]; Wette et al. [8]; Dubin [9]; Serio [10]; Tan et al. [11]; Moolgovkar et al. [12]; Hanin et al. [13]; Rinaldo [14], etc., Studies of two stage stochastic modeling of cancer growth with linear birth and death processes was initiated by Birkhead [15] Later on Tirupathi Rao et al. [16], Madhavi et al. [17], Tirupathi Rao et al. [18], [19], [20] and [21] have developed several two stage stochastic models for cancer cell growth. The above reported research work has focused up to the two stage stochastic modeling for studying the growth of cancer cell. However, three stage stochastic modeling is considered to be more appropriate and will provide suitable insights of the cancer growth.
This study is focused on modeling the three stage cancer growth using trivariate Poisson processes. The first stage is considered to be the cell is in normal status. The existing normal cells may generate some more normal cells, some of them may be transformed in to mutant cells or a part of them may be exposed to the risk of death. The second stage is considered to be a cell is in the status of mutant (transformed from normal). These cells may generate some more mutant cells (benign cells) with the same intensity of growth, some of the mutant cells may further transformed into a cancerous cell (malignant cell) or a part of the mutant cells may exposed to the event of death. The third stage is considered to be the cell is in malignant state. These cells may further produce some more malignant cells with faster rate or a part of them may be exposed to the event of death. Stochastic modeling is carried out under the biological and theoretical assumptions of cancer pathophysiology as the happenings of the cell division are purely random and influenced by chance factors. The following is a schematic diagram for cancer growth in three stages.
 

STOCHASTIC MODEL FOR CANCER GROWTH
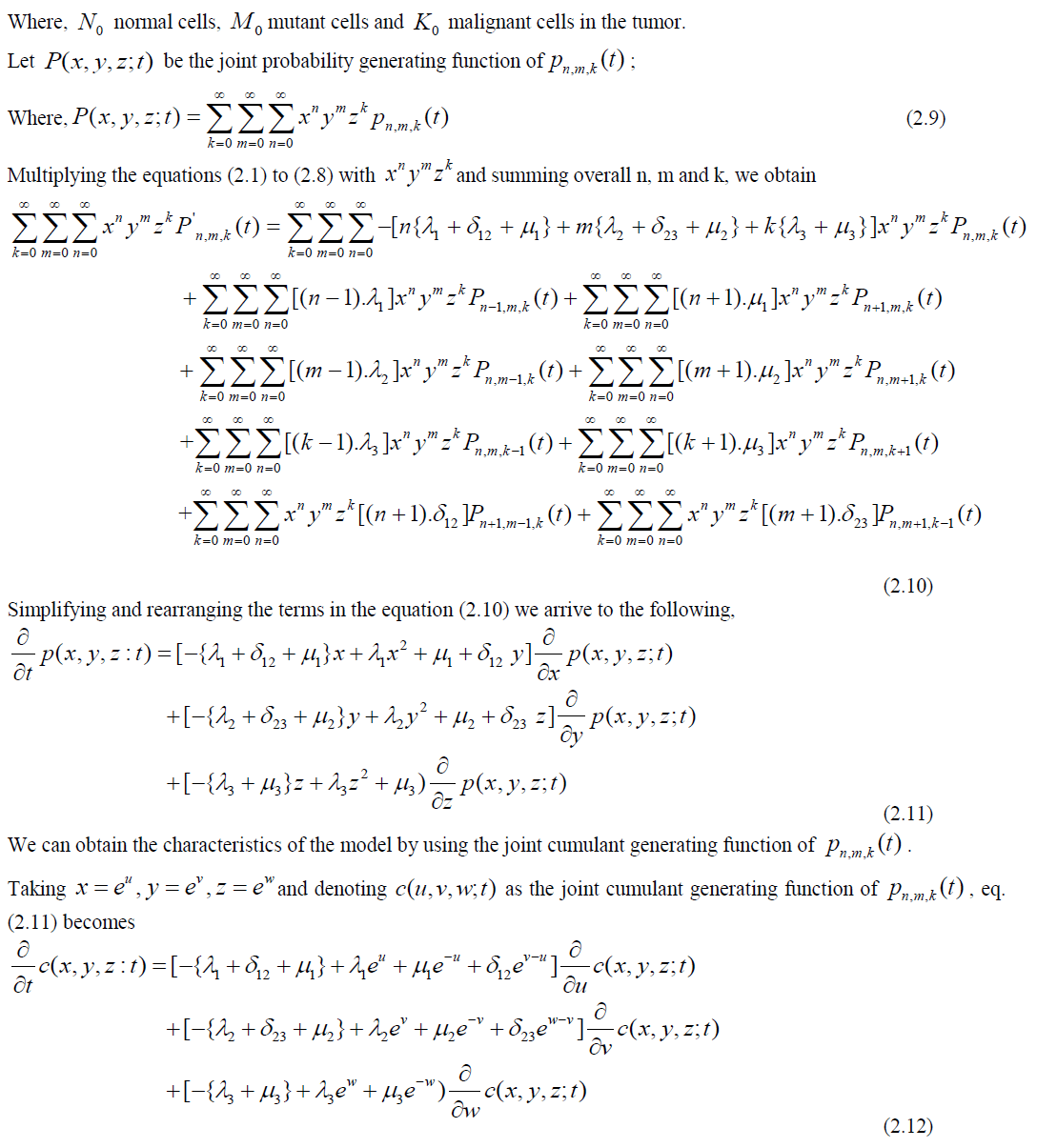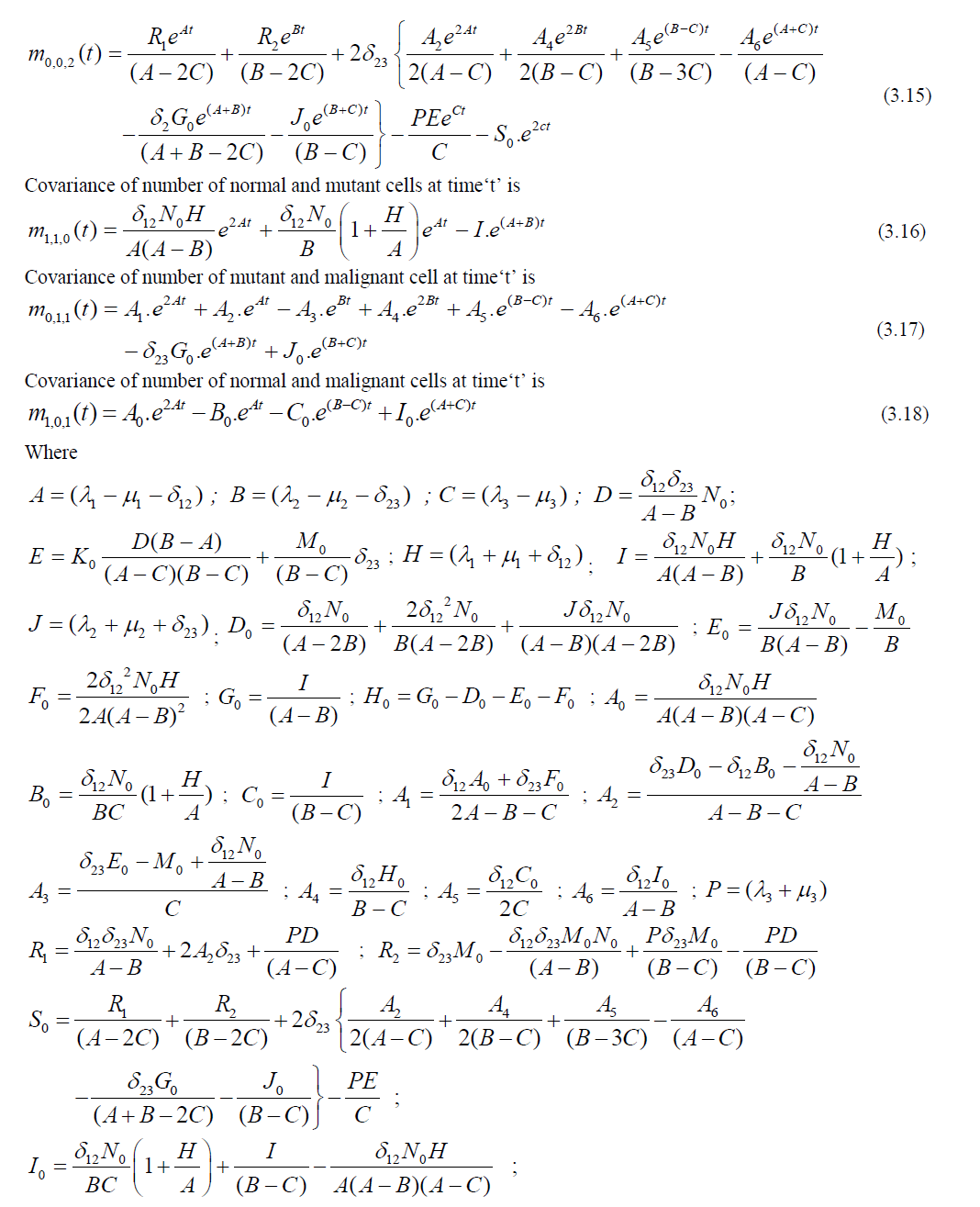image
image
image
image
image
image

ACKNOWLEDGEMENTS
The authors are thankful to acknowledge the funding agency to extract this study as the first author is the principal investigator of a major research project work entitled “Studies on Stochastic Models for Cancer Growth and its Applications with Optimal Drug Administration in Chemotherapy” sponsored by the Scientific and Engineering Research Board (SERB), Department of Science and Technology (DST), Govt. of India.

References
  1. Mayneord, W.V, “On a law of growth of Jenson‟s rat sarcoma”, Amer.J.Cancer, Vol. 16, pp. 841-846, 1932
  2. Kendall, D.G, “Birth and Death processes and the theory of carcinogenesis”, Biometrics, Vol.47, pp. 13 -121, 1960
  3. Neyman, J. Scott, E, “Statistical aspects of the problem of carcinogenesis”, Fifth Berkely Symposium on Mathematical statistics and Probability”, Uni. Of Calif. Press, Berkeley, pp. 745-776, 1967
  4. Marco, L.B., Antino, C.C. and Pier, F.P, “A mathematical model for the evolution of cell population under the action of mutag enic agents”, Math Biosci., Vol.71, pp.19-40, 1984
  5. Murray, J.M, “Some optimal control problems in chemotherapy with toxicity limit”, Math. Biosci., Vol. 100, pp. 49 -67, 1990
  6. Anup Dewanji, Suresh H. Moolgavkar and E. Georg Luebeck, “Two-mutation model for carcinogenesis: Joint analysis of premalignant malignant lesions”, Mathematical Biosciences, Vol. 104, pp. 97-109, 1991
  7. Neyman, J, “A two-step mutation theory of carcinogenesis”, Mimeograph, US National Institute of Health, 1958
  8. Wette, R., Katz, I.N. and Rodin, E.Y, “Stochastic Processes for Solid Tumor Kinetics I. Surface – Regulated Growth”, Mathematical Biosciences, Vol. 19, pp. 231-255, 1974
  9. Dubin, N, “A Stochastic model for immunological feed back in carcinogenesis: analysis and approximations:, Lect. Notes in Biomath, 9, Springer, New York, 1976
  10. Gabriella Serio, “Two-Stage Stochastic Model for Carcinogenesis with Time-Dependent Parameters”, Statistics and Probability, Vol.2, pp. 95-103, 1984
  11. Tan, W.Y. and Gastardo, M.T.C, “On the assessment of effect of environmental agents tumor development by a two stage model of carcinogenesis” Math. Biosci. 74, pp. 143-155, 1985
  12. Moolgavkar, S.H., Dewanji, A. and Venzon, D.J, “A stochastic two stage model for cancer risk assessment I the hazard function and the probability of tumor”; Risk. Anal., Vol.8, pp.383-392, 1988
  13. Hanin, L.G., Rachev, S.T., Tsodikov, A.D. and Yakovlev, A.Yu, “A Stochastic Model of Carcinogenesis and Tumor Size at Detect ion”, Advances in Applied Probability, Vol. 29, No. 3, pp. 607-628, 1997
  14. Rinaldo B. Schinazi, “A Stochastic Model for Cancer Risk”, Genetics society of America, Vol.174, pp. 545-547, 2006
  15. Birkhead, B.G, “The transient solution of the linear birth, death process with random spontaneous mutation”, Math. Biosci. 82 , pp.193-200, 1986
  16. Tirupathi Rao, P. and Srinivasa Rao, K, “Two Stage Stochastic Model for Cancer Cell Growth”, Indian Journal of Mathematics Sciences, Vol.2, No.2, pp.153-168, 2006
  17. Madhavi, K., Tirupatihi Rao, P. and Ramakrishna, S, “Stochastic modeling on stage Dependent Mutant cell growth”, International Journal of Computational Science and Mathematics. Vol 4(3), pp. 187-196, 2012
  18. Tirupathi Rao, P., Madhavi, K. and Kalpana, P, “Two Stage Mutant Cell Growth through Stochastic Modeling”, Global Journal of Mathematical Sciences: Theory and Practical, Vol. 3. No. 2, pp. 101-110, 2011
  19. Madhavi, K., Tirupathi Rao, P. and Ramakrishna, S, “Stochastic Modeling on Stage Dependent Mutant Cell Growth”, Internationa l Journal of Computational Science and Mathematics, Vol. 4, No. 3, pp. 187-196, 2012a
  20. Tirupathi Rao, P., Flora Evangil, D. and Madhavi, K, “Stochastic Programming on Optimal Drug Administration for Two stage Cancer treatment problems”, International Journal of Green Computing, Vol.3(1), pp. 1-10, 2012c
  21. Tirupathi Rao, P., Madhavi, K., Naveen Kumar, B.N. and Reddy, P.R.S, “Stochastic Modeling for treatment Malignancy Growth”, International Journal of Advanced scientific and technical research”, Vol. 4, Issue 2, pp. 607-618, 2012b