ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
|
Jyotsna Patil1, Sunita Jadhav2 Assistant Professor, Department of EXTC, SCOE, Mumbai University, Maharashtra, India1 Assistant Professor, Department of EXTC, SCOE, Mumbai University, Maharashtra, India2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Visual information transmitted in the form of digital images is becoming a major method of communication in the modern age, but the image obtained after transmission is often corrupted with noise. The received image needs processing before it can be used in applications. Image denoising involves the manipulation of the image data to produce a visually high quality image. This paper reviews the Noise models, Noise types and classification of image denoising techniques. This paper presents a comparative analysis of various noise suppression algorithms.
Keywords |
||||||||||
| Image denoising, Noise types, Spatial domain filtering, Wavelet transform | ||||||||||
INTRODUCTION |
||||||||||
| Digital images play an important in research and technology such as geographical information systems as well as it is the most vital part in the field of medical science such as ultrasound imaging, X-ray imaging, Computer tomography and MRI. A very large portion of digital image processing includes image restoration. Image restoration is a method of removal or reduction of degradation that are incurred during the image capturing. Degradation comes from blurring as well as noise due to the electronic and photometric sources. Blurring is the form of bandwidth reduction of images caused by imperfect image formation process such as relative motion between camera and original scene or by an optical system that is out of focus. Noise is unwanted signal that interferes with the original signal and degrades the visual quality of digital image. The main sources of noise in digital images are imperfect instruments, problem with data acquisition process, interference natural phenomena, transmission and compression [1]. Image denoising forms the pre-processing step in the field of photography, research, technology and medical science, where somehow image has been degraded and needs to be restored before further processing. Image denoising is still a challenging problem for researchers as image denoising causes blurring and introduces artifacts. Different types of images inherit different types of noise and different noise models are used to present different noise types. Denoising method tends to be problem specific and depends upon the type of image and noise model. Various noise types, noise models and denoising methods are discussed in this paper. | ||||||||||
II. NOISE MODEL |
||||||||||
| Noise is present in image either in additive or multiplicative form [2]. | ||||||||||
| A. Additive Noise Model | ||||||||||
| Noise signal that is additive in nature gets added to the original signal to produce a corrupted noisy signal and follows the following model: | ||||||||||
| W (x, y) = s(x, y) + n(x, y) (1) | ||||||||||
| B. Multiplicative Noise Model | ||||||||||
| In this model, noise signal gets multiplied to the original signal. The multiplicative noise model follows the following rule: | ||||||||||
| W (x, y) = s(x, y) × n(x, y) (2) | ||||||||||
| Where, s(x, y) is the original image intensity and n(x, y) denotes the noise introduced to produce the corrupted signal w(x, y) at (x, y) pixel location. | ||||||||||
III. TYPES OF NOISE |
||||||||||
| Various types of noise have their own characteristics and are inherent in images in different ways [3]. | ||||||||||
| 1. Gaussian Noise | ||||||||||
| Gaussian noise is evenly distributed over the signal. This means that each pixel in the noisy image is the sum of the true pixel value and a random Gaussian distributed noise value. As the name indicates, this type of noise has a Gaussian distribution, which has a bell shaped probability distribution function given by, | ||||||||||
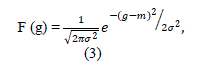 |
||||||||||
| Where g represents the gray level, m is the mean or average of the function and σ is the standard deviation of the noise. Graphically, it is represented as shown in Figure 1.1. When introduced into an image, Gaussian noise with zero mean and variance as 0.05 would look as in Image 1.1. Image 2.2 illustrates the Gaussian noise with mean (variance) as 1.5 (10) over a base image with a constant pixel value of 100. | ||||||||||
| 2. Salt and Pepper Noise | ||||||||||
| Salt and Pepper [3] is an impulse type of noise and is also referred to as intensity spikes. It is generally caused due to errors in transmission. This is caused generally due to errors in data transmission. It has only two possible values, a and b. The probability of each is typically less than 0.1. The corrupted pixels are set alternatively to the minimum or to the maximum value, giving the image a “salt and pepper” like appearance. Unaffected pixels remain unchanged. For an 8- bit image, the typical value for pepper noise is 0 and for salt noise 255. The salt and pepper noise is generally caused by malfunctioning of pixel elements in the camera sensors, faulty memory locations, or timing errors in the digitization process. The probability density function for this type of noise is shown in Figure 2.2. | ||||||||||
| 2.3. Speckle Noise | ||||||||||
| Speckle noise [4] [5] is multiplicative noise. This type of noise occurs in almost all coherent imaging systems such as laser, acoustics and SAR (Synthetic Aperture Radar) imagery. The source of this noise is attributed to random interference between the coherent returns. Fully developed speckle noise has the characteristic of multiplicative noise. Speckle noise follows a gamma distribution and is given as: | ||||||||||
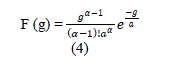 |
||||||||||
| Where variance is ��2�� and g is the gray level | ||||||||||
| On an image, speckle noise (with variance 0.05) looks as shown in Image 2.4. The gamma distribution is given below in Figure 2.3. | ||||||||||
| 2.3.4 Brownian Noise | ||||||||||
| Brownian noise comes under the category of fractal or 1/f noises. The mathematical model for 1/f noise is fractional Brownian motion. Fractal Brownian motion is a non-stationary stochastic process that follows a normal distribution. Brownian noise is a special case of 1/f noise. It is obtained by integrating white noise. It can be graphically represented as shown in Figure 2.4. | ||||||||||
IV. DENOISING TECHNIQUES |
||||||||||
| Various denoising techniques have been proposed so far and their application depends upon the type of image and noise present in the image. Image denoising is classified in two categories: | ||||||||||
| 1. Spatial domain filtering | ||||||||||
| This is the traditional way to remove the noise from the digital images to employ the spatial filters. Spatial domain filtering is further classified into linear filters and non-linear filters [6]. | ||||||||||
| 1.1 Linear Filters | ||||||||||
| A mean filter is the optimal linear for Gaussian noise in the sense of mean square error. Linear filters tend to blur sharp edges, destroy lines and other fine details of image. It includes Mean filter and Wiener filter [6]. | ||||||||||
| A. Mean Filter | ||||||||||
| A mean filter acts on an image by smoothing it; that is, it reduces the intensity variation between adjacent pixels. The mean filter is nothing but a simple sliding window spatial filter that replaces the centre value in the window with the average of all the neighbouring pixel values including it. By doing this, it replaces pixels that are unrepresentative of their surroundings. It is implemented with a convolution mask, which provides a result that is a weighted sum of the values of a pixel and its neighbours. It is also called a linear filter. The mask or kernel is a square. Often a 3× 3 square kernel is used. If the coefficients of the mask sum up to one, then the average brightness of the image is not changed. If the coefficients sum to zero, the average brightness is lost, and it returns a dark image. The mean or average filter works on the shift-multiply-sum principle. This principle in the two-dimensional image can be represented as shown below (refer to Figure 3.1). | ||||||||||
| Multiply and sum for the pixel at (4, 3) = h1w32 + h2w33 + h3w34 + h4w42 + h5w43 + h6w44 + h7w52 + h8w53 + h9w54 | ||||||||||
| The mask used here is a 3× 3 kernel shown in Figure 3.2. Note that the coefficients of this mask sum to one, so the image brightness is retained, and the coefficients are all positive, so it will tend to blur the image. | ||||||||||
| Example 3.1: For the following 3×3 neighbourhood, mean filtering is applied by convoluting it with the filter mask shown in Figure 3.2. | ||||||||||
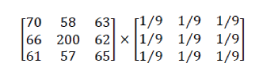 |
||||||||||
| This provides a calculated value of 78. Note that the centre value 200, in the pixel matrix, is replaced with this calculated value 78. This clearly demonstrates the mean filtering process. Computing the straightforward convolution of an image with this kernel carries out the mean filtering process. It is effective when the noise in the image is of impulsive type. The averaging filter works like a low pass filter, and it does not allow the high frequency components present in the noise to pass through. It is to be noted that larger kernels of size 5× 5 or 7×7 produces more denoising but make the image more blurred. A trade off is to be made between the kernel size and the amount of denoising. The filter discussed above is also known as a constant coefficient filter because the weight matrix does not change during the whole process. Mean filters are popular for their simplicity and ease of implementation. We have implemented the averaging filter using Matlab 6.1. The pixel values of an image “cameraman.tif” are read into the program by using the function imread().This image is of size 256× 256. Salt and pepper noise is added to this image by using the function imnoise() . The pixel values of this corrupted image are copied into a 2-dimentional array of size 256× 256. A 3×3 weight matrix is initialized. Selecting a 3× 3 window over the 256× 256 pixel matrix, the weighted sum of the selected window is computed. The result replaces the center pixel in the window. For the next iteration, the window moves by one column to the right. The window movements are considered in the horizontal direction first and then in the vertical direction until all the pixels are covered. The modified pixel matrix is now converted to the image format with the help of the function imwrite(). Image 3.1 is the one corrupted with salt and pepper noise with a variance of 0.05. The output image after Image 3.1 is subjected to mean filtering is shown in Image 3.2. It can be observed from the output that the noise dominating in Image 3.1 is reduced in Image 3.2. The white and dark pixel values of the noise are changed to be closer to the pixel values of the surrounding ones. Also, the brightness of the input image remains unchanged because of the use of the mask, whose coefficients sum up to the value one. The mean filter is used in applications where the noise in certain regions of the image needs to be removed. In other words, the mean filter is useful when only a part of the image needs to be processed. | ||||||||||
| B. Weiner Filter | ||||||||||
| Weiner filtering [8] method requires the information about the spectra of noise and original signal and it works well only if the underlying signal is smooth. Weiner method implements the spatial smoothing and its model complexity control corresponds to the choosing the window size. H (u, v) is the degradation function and H(u, v)* is its conjugate complex. G(u, v) is the degraded image. Functions Sf (u, v) and Sn (u, v) are power spectra of original image and the noise. Wiener Filter assumes noise and power spectra of object a priori. | ||||||||||
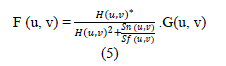 |
||||||||||
| 1.2. Non- Linear | ||||||||||
| With the non-linear filter, noise is removed without any attempts to explicitly identify it. Spatial filters employ a low pass filtering on the group of pixels with the assumption that noise occupies the higher region of frequency spectrum. Generally spatial filters remove the noise to reasonable extent but at the cost of blurring the images which in turn makes the edges in the picture invisible. | ||||||||||
| A. Median Filter | ||||||||||
| Median filter [7] follows the moving window principle and uses 3×3, 5×5 or 7×7 window. The median of window is calculated and the centre pixel value of the window is replaced with that value. | ||||||||||
| 2. Transform domain filtering | ||||||||||
| The transform domain filtering can be subdivided into data adaptive and non-adaptive filters. Transform domain mainly includes wavelet based filtering techniques [6]. | ||||||||||
| 2.1. Wavelet Transform | ||||||||||
| Filtering operations in the wavelet domain can be subdivided into linear and nonlinear methods. | ||||||||||
| A. Linear Filters | ||||||||||
| Linear filters such as Wiener filter in the wavelet domain yield optimal results when the signal corruption can be modelled as a Gaussian process and the accuracy criterion is the mean square error (MSE) [9, 10]. However, designing a filter based on this assumption frequently results in a filtered image that is more visually displeasing than the original noisy signal, even though the filtering operation successfully reduces the MSE. In [11] a wavelet-domain spatially adaptive FIR Wiener filtering for image denoising is proposed where wiener filtering is performed only within each scale and intra scale filtering is not allowed. | ||||||||||
| B. Non-Linear Threshold Filtering | ||||||||||
| The most investigated domain in denoising using Wavelet Transform is the non-linear coefficient thresholding based methods. The procedure exploits sparsity property of the wavelet transform and the fact that the Wavelet Transform maps white noise in the signal domain to white noise in the transform domain. Thus, while signal energy becomes more concentrated into fewer coefficients in the transform domain, noise energy does not. It is this important principle that enables the separation of signal from noise. The procedure in which small coefficients are removed while others are left untouched is called Hard Thresholding [12]. But the method generates spurious blips, better known as artifacts, in the images as a result of unsuccessful attempts of removing moderately large noise coefficients. To overcome the demerits of hard thresholding, wavelet transform using soft thresholding was also introduced in [12]. In this scheme, coefficients above the threshold are shrunk by the absolute value of the threshold itself. Similar to soft thresholding, other techniques of applying thresholds are semi-soft thresholding and Garrote thresholding [13]. Most of the wavelet shrinkage literature is based on methods for choosing the optimal threshold which can be adaptive or non-adaptive to the image. | ||||||||||
| a. Non-Adaptive thresholds | ||||||||||
| VISUshrink [14] is non-adaptive universal threshold, which depends only on number of data points. It has asymptotic equivalence suggesting best performance in terms of MSE when the number of pixels reaches infinity. VISUshrink is known to yield overly smoothed images because its threshold choice can be unwarrantedly large due to its dependence on the number of pixels in the image. | ||||||||||
| b. Adaptive Thresholds | ||||||||||
| SUREShrink [14] uses a hybrid of the universal threshold and the SURE [Stein‟s Unbiased Risk Estimator] threshold and performs better than VISUShrink. BayesShrink [15, 16] minimizes the Baye‟s Risk Estimator function assuming Generalized Gaussian prior and thus yielding data adaptive threshold. BayesShrink outperforms SUREShrink most of the times. Cross Validation [17] replaces wavelet coefficient with the weighted average of neighbourhood coefficients to minimize generalized cross validation (GCV) function providing optimum threshold for every coefficient. The assumption that one can distinguish noise from the signal solely based on coefficient magnitudes is violated when noise levels are higher than signal magnitudes. Under this high noise circumstance, the spatial configuration of neighbouring wavelet coefficients can play an important role in noise-signal classifications. Signals tend to form meaningful features (e.g. straight lines, curves), while noisy coefficients often scatter randomly. | ||||||||||
| C. Non-orthogonal Wavelet Transforms | ||||||||||
| Undecimated Wavelet Transform (UDWT) has also been used for decomposing the signal to provide visually better solution. Since UDWT is shift invariant it avoids visual artifacts such as pseudo-Gibbs phenomenon. Though the improvement in results is much higher, use of UDWT adds a large overhead of computations thus making it less feasible. In [18] normal hard/soft thresholding was extended to Shift Invariant Discrete Wavelet Transform. In [19] Shift Invariant Wavelet Packet Decomposition (SIWPD) is exploited to obtain number of basis functions. Then using Minimum Description Length principle the Best Basis Function was found out which yielded smallest code length required for description of the given data. Then, thresholding was applied to denoise the data. In addition to UDWT, use of Multiwavelets is explored which further enhances the performance but further increases the computation complexity. The Multiwavelets are obtained by applying more than one mother function (scaling function) to given dataset. Multiwavelets possess properties such as short support, symmetry, and the most importantly higher order of vanishing moments. This combination of shift invariance & Multiwavelets is implemented in [20] which give superior results for the Lena image in context of MSE. | ||||||||||
| D. Wavelet Coefficient Model | ||||||||||
| This approach focuses on exploiting the multiresolution properties of Wavelet Transform. This technique identifies close correlation of signal at different resolutions by observing the signal across multiple resolutions. This method produces excellent output but is computationally much more complex and expensive. The modelling of the wavelet coefficients can either be deterministic or statistical. | ||||||||||
| a. Deterministic | ||||||||||
| The Deterministic method of modelling involves creating tree structure of wavelet coefficients with every level in the tree representing each scale of transformation and nodes representing the wavelet coefficients. This approach is adopted in [21]. The optimal tree approximation displays a hierarchical interpretation of wavelet decomposition. Wavelet coefficients of singularities have large wavelet coefficients that persist along the branches of tree. Thus if a wavelet coefficient has strong presence at particular node then in case of it being signal, its presence should be more pronounced at its parent nodes. If it is noisy coefficient, for instance spurious blip, then such consistent presence will be missing. Lu et al. [22], tracked wavelet local maxima in scale space, by using a tree structure. Other denoising method based on wavelet coefficient trees is proposed by Donoho [23]. | ||||||||||
| b. Statistical Modelling of Wavelet Coefficients | ||||||||||
| This approach focuses on some more interesting and appealing properties of the Wavelet Transform such as multiscale correlation between the wavelet coefficients, local correlation between neighbourhood coefficients etc. This approach has an inherent goal of perfecting the exact modelling of image data with use of Wavelet Transform. A good review of statistical properties of wavelet coefficients can be found in [24] and [25]. The following two techniques exploit the statistical properties of the wavelet coefficients based on a probabilistic model. | ||||||||||
| I. Marginal Probabilistic Model | ||||||||||
| A number of researchers have developed homogeneous local probability models for images in the wavelet domain. Specifically, the marginal distributions of wavelet coefficients are highly kurtosis, and usually have a marked peak at zero and heavy tails. The Gaussian mixture model (GMM) [26] and the generalized Gaussian distribution (GGD) [27] are commonly used to model the wavelet coefficients distribution. Although GGD is more accurate, GMM is simpler to use. In [28], authors proposed a methodology in which the wavelet coefficients are assumed to be conditionally independent zero-mean Gaussian random variables, with variances modelled as identically distributed, highly correlated random variables. An approximate Maximum A Posterior (MAP) Probability rule is used to estimate marginal prior distribution of wavelet coefficient variances. All these methods mentioned above require a noise estimate, which may be difficult to obtain in practical applications. Simon celli and Adel son [29] used a two parameter generalized Laplacian distribution for the wavelet coefficients of the image, which is estimated from the noisy observations. Chang et al. [30] proposed the use of adaptive wavelet thresholding for image denoising, by modelling the wavelet coefficients as a generalized Gaussian random variable, whose parameters are estimated locally (i.e., within a given neighbourhood). | ||||||||||
| II. Joint Probabilistic Model | ||||||||||
| Hidden Markov Models (HMM) [31] models are efficient in capturing inter-scale dependencies, whereas Random Markov Field [32] models are more efficient to capture intra scale correlations. The complexity of local structures is not well described by Random Markov Gaussian densities whereas Hidden Markov Models can be used to capture higher order statistics. The correlation between coefficients at same scale but residing in a close neighbourhood are modelled by Hidden Markov Chain Model where as the correlation between coefficients across the chain is modelled by Hidden Markov Trees. Once the correlation is captured by HMM, Expectation Maximization is used to estimate the required parameters and from those, denoised signal is estimated from noisy observation using well known MAP estimator. In [33], a model is described in which each neighbourhood of wavelet coefficients is described as a Gaussian scale mixture (GSM) which is a product of a Gaussian random vector, and an independent hidden random scalar multiplier. Stella et al. [34] described the joint densities of clusters of wavelet coefficients as a Gaussian scale mixture, and developed a maximum likelihood solution for estimating relevant wavelet coefficients from the noisy observations. Another approach that uses a Markov random field model for wavelet coefficients was proposed by Jansen and Bulthel [35]. A disadvantage of HMT is the computational burden of the training stage. In order to overcome this computational problem, a simplified HMT, named as uHMT [25], was proposed. | ||||||||||
| 3. Data-Adaptive Transforms | ||||||||||
| Recently a new method called Independent Component Analysis (ICA) has gained wide spread attention. The ICA method was successfully implemented in [36, 37] in denoising Non-Gaussian data. One exceptional merit of using ICA is it‟s assumption of signal to be Non-Gaussian which helps to denoise images with Non-Gaussian as well as Gaussian distribution. Drawbacks of ICA based methods as compared to wavelet based methods are the computational cost because it uses a sliding window and it requires sample of noise free data or at least two image frames of the same scene. In some applications, it might be difficult to obtain the noise free training data. | ||||||||||
V. CONCLUSION |
||||||||||
| The comparative study of various denoising techniques for digital images shows that wavelet filters outperforms the other standard spatial domain filters. Although all the spatial filters perform well on digital images but they have some constraints regarding resolution degradation. These filters operate by smoothing over a fixed window and it produces artifacts around the object and sometimes causes over smoothing thus causing blurring of image. Wavelet transform is best suited for performance because of its properties like sparsity, multi resolution and multi scale nature. Thresholding techniques used with discrete wavelet are simplest to implement. | ||||||||||
Tables at a glance |
||||||||||
|
||||||||||
Figures at a glance |
||||||||||
|
||||||||||