A DETERMINISTIC APPROACH FOR ROUTING THROUGH POLYCHROMATIC SETS IN WIRELESS ADHOC NETWORKS

Abstract

Graph Theory is one of the basic methodologies opted for analysing computer networks such as Adhoc networks, sensor networks .Conventional Graph theory is not an proper approach for designing the wireless networks because variety of nodes and wireless link may exist. Even the usage of random graph and weighted graph may not properly model the complex wireless networks as they merely stand on a single property. This leads to the introduction of the concept of Poly chromatic sets in modelling complex wireless networks. In this paper we put forward the concept of Poly chromatic set theory which will maintain the properties of each node that support for efficient routing, and the results have proven that it is a perfect tool to determine the nodes in wireless networks.

Keywords

Poly-chromatic sets, routing, wireless networks, random graph, weighted graph.

INTRODUCTION

Conventional graph theory and Set theory are the basic approaches for designing the infrastructure of network. In a graph theory a graph is represented as G = (V, E), where V represents a set of vertices and G represents the set of edges. In recent years most of the applications in the area of networks are represented based on the random graph [3] and weighted graph [2]. In wireless networks unit disk graphs [1] plays a major role, as nodes transmission takes place dynamically. So, we represent the represent the node when there is an edge of unit distance i.e., the nodes within the communication range are identified in unit disk graph, where as random graph is applied when there exists probability of edges. Random graphs are widely used in complex networks. The main drawback is designing the network based on unit disk graph, random graph and weight Graph is that it emphasizes on existence, probability and weight, but the modern complex networks needs a better tool that has key knowledge on network nodes and links such as capacity, lifetime and properties of nodes. This made V .V.Pavlov introduced a new graph theory for modelling the complex manufacturing system. Poly chromatic sets defines the properties of each elements in the whole set. So, the concept of Poly chromatic set theory [4][5][6] can be used to describe various properties of network nodes and links for designing complex wireless networks. Our proposed method makes use of this poly chromatic set theory to model the wireless network for achieving simplicity and fast convergence, which supports for efficient routing in wireless networks.

II. RELATED WORK

In conventional set theory , a set is represented as a collection of elements [9]such that S={s1,s2,s3………sn} where S represents set and s1,s2,s3….. sn are elements of the set S having similar properties for example if we consider fruits as a set S, then all the different types of fruits comes under the set S. But there is a draw back in representing by conventional graph theory i.e., for example if we consider apple, orange it comes under set S, but the properties of both fruits vary. Apple comes under non-citrus whereas Orange comes under citrus fruit. The difference is notified in the set. So, the conventional set theory doesn’t describe the properties of each element in the set. This leads to the introduction of the concept of Poly chromatic sets in modelling wireless networks, where it defines each and every element of the set and its properties. Each property is denoted by colour. The elements having different properties are represented in different colours and each set may have any number different colours [7][8].

S= {s1,s2,s3……,sn}.

By using the concepts of Poly chromatic set theory, we can describe the properties of each and every element in the set. For s1, it is denoted as F(s1) such that

F(s1) = { F1(s1) , F2(s1), F3(s1), Fm(s1)……… Fn (s1)}

III. DESIGNING WIRELESS ADHOC NETWORKS

In wireless networks, nodes splits into clusters where each cluster has a cluster head which organizes all the nodes in the cluster. Here we will adapt hierarchical model for representing the nodes where the lower layer contains clusters and in the next layer the cluster heads of the lower layers will be there, likewise the process continuous until a single cluster head node exists at particular level.

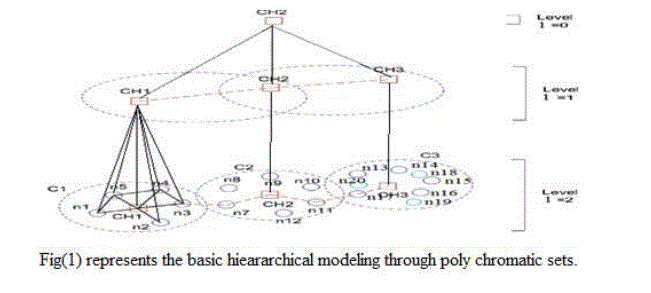By adapting Poly chromatic set theory in designing the wireless networks we define an element in the set S as s1 and its colouring set i.e., set of properties of element s1is represented as F(s1).Then the wireless network having m nodes is described as

<si F(si )> ,i=1,2,3….n.

Finally, a node is defined as s(l,il,jl-1) where l represents the level of the node. il denotes that it is ith node at level l and jl-1 denotes the jth node(parent node) at a level l-1.and F(s(l,il,jl-1),represents the properties such as index ,parent node ,child node and so on. Thus the hierarchical model for wireless networks using poly chromatic set theory can be represented as

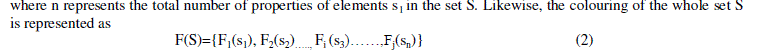Now, let us come to know in brief about how we adapt the Poly chromatic set theory [8]. in wireless networks. In the Fig(1),we have considered 20 nodes and we split the nodes in the network area into 3 clusters In cluster1 there are 6 nodes .Based on the relative positions we will represent in Poly chromatic set matrix. In this matrix representation if there is a link we will represent by Boolean value 1.Otherwise,null i.e., 0.We will calculate index and make it as second unified colour of a cluster1 by means of Adhoc-On-demand Distance Vector routing algorithm[11].In hierarchical model for representing the nodes where the lower layer contains clusters and in the next layer the cluster heads of the lower layers will be there, likewise the process continuous until a single cluster head node exists at particular level, and cluster head will manages the entire nodes within that cluster. By using Poly chromatic set theory we can easily locate the nodes by s(l,il ,jl-1).for example s(4,2 ,3) represents the node is at level 4 where as its father node is at level 2 and it is at cluster 3.and further routing takes place which is mentioned in section 4.The third unified color Sp defines the prior nodes of a particular node. In this case s1 is a source node and s3 is a destination node of a cluster1, here s6 acts a prior node to s1 since the next hop of s6 is s3 which is a destination node. Likewise, we will calculate Sc for the child nodes. and the SCH as well, here s6 would be the cluster head(CH)[14].We will calculate in the similar way for all other clusters in the network area.

IV. ROUTING SCHEME THROUGH POLY CHROMATIC SET THEORY

Generally, in routing of wireless networks hierarchical routing scheme is mostly preferred since the flat routing scheme [12] has large amount of packet overhead which results in low scalability. So, in hierarchical routing there are two techniques they are dynamic routing technique which has fisheye state routing and inter-zone routing protocol. The main advantage of implementing on hierarchical routing is less control packet overhead and scalability. We basically prefer hierarchical routing for modelling through poly chromatic sets. In the routing we will perform network portioning and clustering. Here, the cluster head selection plays a major role. The cluster head is selected based on link quality [13], which is calculated as follows

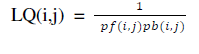The link quality(LQ(i,j)) for node si to sj is calculated by making use of forward delivery ratio(pf) and backward delivery ratio(pb) from node si to sj .Based on the resultant value, link quality is assigned as an index.

A. Routing

The second most import criteria is routing. In this scheme we prefer AODV[10] approach , in addition to this if we want to provide communication between source node and the destination node .then probably the source node will requests CH to check whether the destination node is within that cluster node or not. If the destination node is within that cluster node then it will transfer the data, if not, then it will check on to the next layer for destination node and process continues until it finds the destination node in any of the clusters .

V. SIMULATION RESULTS

For the performance evaluation of our proposed system we are following the below parameters in the ns2 simulator environment.

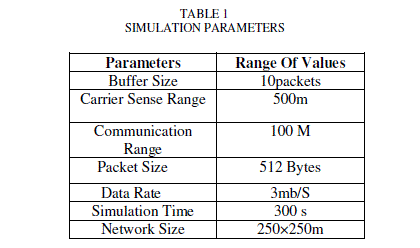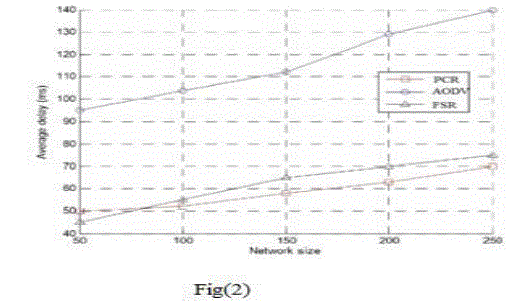In fig (2) here, we compare the results for AODV,FSR(fisheye state routing) and our proposed pcr(poly chromatic routing).which is a modified scheme of AODV . The results have shown that the delay remains constant for PCR when compared to the other two routing schemes.

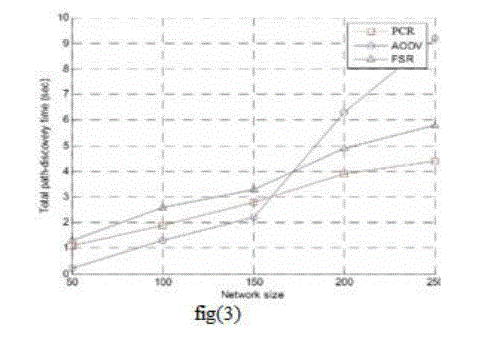similarly, in fig(3) we consider the network size as a function of total path discovery, by using our proposed scheme the nodes in the network area can be discovered efficiently in shorter period of time when compared to the other two routing schemes

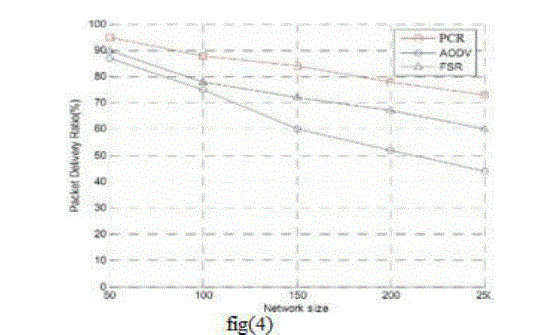In Fig(4) we compared network size with respect to the packet delivery ratio .we can observe the drastic change over the other two schemes.

VI. CONCLUSION

In this paper we proposed hierarchical routing scheme based on the Poly chromatic set theory which has become an optimistic tool for efficient routing in wireless networks, since discovering the nodes in wireless sensor networks is an hectic task. Simulation results validated that our proposed scheme outperforms hierarchical routing. In future we are going to implement it for a large complex networks which includes more number of levels.

VII. ACKNOWLEDGEMENT

We sincerely express our gratitude to K. Karthikeyan, Associate Professor, SAS, VIT University, Vellore, who has been an excellent guide and also a great source of inspiration to our work.

References

1. [1] Gadouleau and S. Riis, “Graph-theoretical constructions for graph entropy and network coding based communications,” IEEE Trans. Inform. Theory, vol. 57, no. 10, pp. 6703–6717, Oct. 2011
2. [2] M. M. Zavlanos, M. B. Egerstedt, and G. J. Pappas, “Graph-theoretic connectivity control of mobile robot networks,” Proc. IEEE, vol. 99, no. 9, pp. 1525–1540, Sep. 2011
3. [3] X. Li, X. Xu, F. Zou, H. Du, P. Wan, Y. Wang, and W. Wu, “A PTAS for node-weighted Steiner tree in unit disk graphs,” in Proc. 3rd Int. Conf. Combinat. Optimiz. Applicat. vol. 5573. 2009, pp. 36–48
4. [4] V. Pavlov, “Polychromatic graph of mathematics simulation for technical system,” in Proc. Sci. Tech. Conf., 1988, pp. 8–10
5. [5] V. V. Pavlov, “Mathematics simulation of discrete production system,” Inform. Technol., pp. 15–19, 1995
6. [6] V. V. Pavlov,” Polychromatic Sets and Graphs for CALS Technology”. Moscow, Russia: STANKIN Press, 2000
7. [7] S. Li and X. Wang, “Polychromatic set theory-based spectrum ac-cess in cognitive radios,” IET Commun., vol. 6, no. 8, pp. 909–916, 2012
8. [8] Z. Li and L. Xu, “Polychromatic sets and its application in simulating complex objects and systems,” Comput. Oper. Res., vol. 30, no. 6, pp. 851–860, 2003
9. [9] G. Cantor, “Uber eine Eigenschaft des Inbegriffes aller reellen algebrais-chen zahlen,” Crelles J. Mathematik, vol. 77, pp. 258–262, 1874
10. [10] C. K. Toh, A.-N. Le, and Y.-Z. Cho, “Load balanced routing protocols for ad hoc mobile wireless networks,” IEEE Commun. Mag., vol. 47, no. 8, pp. 78–84, Aug. 2009
11. [11] S. Lee, E. M. Belding-Royer, and C. E. Perkins, “Scalability study of the ad-hoc on-demand distance vector routing protocol,” ACM/Wiley Int. J. Netw. Manag., vol. 13, no. 2, pp. 97–114, 2003
12. [12] C. Lim, S. Bohacek, J. P. Hespanha, and K. Obraczka, “Hierarchical max-flow routing,” in Proc. IEEE Global Telecommun. Conf., vol. 1. Dec. 2005, pp. 545–550
13. [13] D. D. Couto, D. Aguayo, J. Bicket, and R. Morris, “A high-throughput path metric for multi-hop wireless routing,” in Proceedings of the ACM International Conference on Mobile Computing and Networking (MOBICOM), Sep. 2003, pp. 134–146
14. [14] T. J. Kwon and M. Gerla, “Efficient flooding with passive clustering (PC) in ad hoc networks,” ACM SIGCOMM Computer Communication Review, vol. 32, no. 1, pp. 44–56, Jan. 2002