A Digital Signature Scheme Based on Pell Equation

Abstract

Elliptic curve digital signature algorithm (ECDSA) is well established digital signature scheme based on the discrete logarithms problems. On the other hand, many cryptosystem has been designed using the Pell Equation. We apply the idea of ECDSA on the solution space of Pell equation to design a digital signature scheme. In this paper we compare the security of our signatures scheme to DSA and ECDSA. Our scheme is as secure as conventional DSA. We show that the signatures scheme based on Pell equation is more efficient than its analogue to elliptic curve i.e. ECDSA.

Keywords

DSA, ECDSA, Pell Equation,Discrete Logarithm Problem.

INTRODUCTION

In 1985, ElGamal [6] proposed a public key cryptosystem and a digital signature scheme based on the difficulty of solving the Discrete Logarithm Problem in the multiplicative group of an appropriate finite field. In 1991, the National Institute of Standards and Technology of USA proposed the Digital Signature Algorithm (DSA) which is an efficient variant of the ElGamal digital signature scheme [14, 17]. The security of DSA is based on discrete logarithms problem. The Elliptic Curve Digital Signature Algorithm (ECDSA) is being proposed as an ANSI standard. Unlike the normal discrete logarithm problem (DLP) and the integer factorization problem (IFP), the elliptic curve discrete logarithm problem (ECDLP) has no sub exponential-time algorithm. For this reason, the strength-per-key-bit is substantially greater in an algorithm that uses elliptic curves. An original ECDSA was proposed in 1992 by Vanstone [18], and its three variants were given in [21, 4]. These signature schemes are basically the analogues of the corresponding ElGamal digital signature schemes [16]. Many variants of ECDSA have been given in [20]. The Pell Equation has existence since a very ancient time in number theory [3]. It has a number of applications in mathematics [7, 19]. In Algebra, it can be used to find regulator of group [2, 11]. Pell Equation has infinite solution and its solution space forms a cyclic group under appropriate group operation. On the basis of this group, many variants of cryptosystem have been designed [19, 5, 15, 8]. In [5] author proposed fast RSA type scheme based on Pell equation in which encryption speed is 1.5 times faster than then standard RSA and the decryption in 2 times faster. In [15] author defined a new operation on the solution space of Pell Equation and proposed three RSA type cryptosystems. In [8] author proposed a PKC whose security is based on DLP. To the best of our knowledge no signature scheme is found in the literature over the Pell's equation. So, our motivation to this article is to construct a digital signature scheme over Pell's equation.

II. PRELIMINARIES

In this section we brief the Pell's equation and Elliptic Curve.

A. Pell Equation: Suppose ������+ is a square free integer. The Diophantine equation ��2 − �� ��2 = 1 ... (2.1.1) is called Pell Equation. The equation has infinite solutions in the real field. The solution of this equation can be found by continued fraction method [19]. By Lagrange theorem [19], once the fundamental solution of Pell Equation is known, one can find its all solutions. Hence, the solution space of (2.1.1) forms a cyclic group, in fact an infinite cyclic group. Now consider equation (2.1.1) under modulo system. Let p be a positive prime number. Consider

III. DIGITAL SIGNATURE ALGORITHM

The DSA was proposed in August 1991 by the U.S. National Institute of Standards and Technology (NIST) and became a U.S. Federal Information Processing Standard (FIPS 186) in 1993. It was the first digital signature scheme accepted as legally binding by a government [17]. The protocol of DSA is as below.

IV. PROPOSED SCHEME

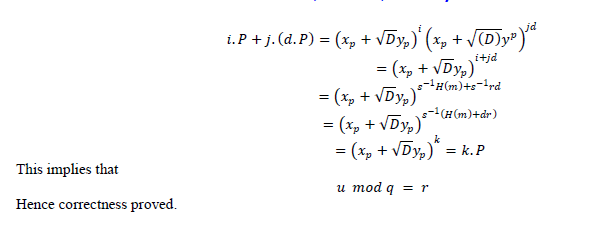E. Security

If we compare the addition operation defined in Elliptic curve and Pell's equation, we see that, the addition operation defined in Elliptic curve is more complicated than the operation defined in Pell's equation. One addition in Elliptic curve requires one inversion and two multiplication where as in Pell's equation requires five multiplication. Since one inversion is computationally equivalent to six multiplication. Due to this point of view we can see that proposed scheme over Pell Equation is more efficient then ECDSA.

V. CONCLUSION

In this article we proposed a digital signatures scheme based on Pell's equation. The proposed scheme is as secure as standard DSA. We have shown that the proposed scheme is two times faster than standard DSA if 2 log p bits are signed at a time and also the proposed scheme is more efficient than the standard ECDSA.

References

1. [1] “Public Key Cryptography for the Financial Services Industry,The Elliptic Curve Digital Signature Algorithm (ECDSA)”, ANSI X9.62,1999.
2. [[2] Buchmann J., “A sub exponential algorithm for the determination of class groups and regulators of algebraic number fields”, S´eminaire de Th´eorie des Nombres, Progress in Mathematics Vol. 91,pp. 27-41, 1989,
3. [[3] BurtonDevid M., Elementry Number Theory, TMH book 2006.
4. [ [4] CaelliW.J.,“Dawson E.P. andReaS.A..Elliptic curve cryptography, and digital signature”, Computer and Security, PKI,Vol18, pp. 47–66, 1999.
5. [ [5] Chen C. Y., Chang C.C., Yang W P.,” Fast RSA type schemes Based on Pell Equations over ZN*”, Proceeding of InternationalConference on Cryptology and Information Security, Taiwan Dec. 1-5, preprint, 1996.
6. [[6] ElGamal T., “A public key cryptosystem and a signature scheme based on discrete logarithm”, IEEE Trans. Inform. Theory, Vol. 31, pp. 469– 472, 1985.
7. [[7] Edward J. B., Pell's Equation: Springer.1999.
8. [ [8] GysinMarc andSeberry Jennifer, “How to use Pell's Equation in cryptography”, Preprint, 1999.
9. [[9] JohnsonD and MenezesAlfred, “The Elliptic Curve Digital Signature Algorithm (ECDSA)- An Enhanced DSA”, Preprint, 1999.
10. [ [10] Hung Zih Liao, Yuan Yuan Shen, “On the Elliptic Curve Digital Signature Algorithm”,Tunghai Science, Vol. 8, pp. 109-126, 2006.
11. [ [11] Lenstra H W, “On the calculation of regulators and class numbers of quadratic fields”, London Math. Soc. Lecture Note Series 56. Birkh¨auser, Boston, pp. 27–41, 1990.
12. [ [12] Menezes A.J., Van Oorschot P.C., Vanstone S.A, “Handbook of Applied Cryptography”, CRC Press, Boca Raton, Florida, 1997.
13. [ [13] Menezes A., “Elliptic curve pubic key cryptosystem”, Kluwer Acad. Pub., 1993.
14. [ [14] “Digital Signature Standard”, National Institute of Standards and Technology (NIST), FIPS Publication 186, 1994
15. [ [15] SahadeoPadhye , “A public Key Cryptosystem based on Pell Equation”, Archive-2005/109, 2005.s
16. [ [16] Stinson D. R., Cryptography Theory and Practice, Chapman & Hall/ CRC, 2000.
17. [ [17] VaudenaySerge, “The Security of DSA and ECDSA Bypassing the Standard Elliptic Curve Certification Scheme”, LNCS 2567, pp. 309–323, 2003.
18. [[18] VanstoneS.,“Responses to NIST’s Proposal”. Communications of the ACM, Vol 35, pp.50–52, 1992.
19. [ [19] JacobsonMichael J., WilliamsHugh C., Solving The Pell Equation; springer, 2009.
20. [ [20] You Lin, Yang Yi Xian, and ZhangChun Qi, “Generalization of Elliptic Curve Digital Signature Schemes”,LNCS Vol.2229, pp. 246-250, 2001.
21. [[21] Zhang Y., Imai. H.,“How to achieve Cost (Signature and Encryption)<< Cost (Signature) + Cost (Encryption)*”, CRYPTO 97, preprint, 1999.