ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Shihabudheen Kunnath 1, Ramarajan A 2 P.G student, Department of Mechanical Engineering, M.E.S college of Engineering, Kuttippuram, Kerala, India1 Asst. Professor, Department of Mechanical Engineering, M.E.S college of Engineering, Kuttippuram, Kerala, India2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The fluid flow problems play a significant role in predicting and understanding the flow pattern in different flow processes. The three dimensional flow analysis is made using an unstructured finite volume technique. The space discretization is carried out using arbitrarily oriented tetrahedral elements. The cell-centered scheme, which is popular in Fluid Dynamics, is directly adopted here. A Least square based methodology is used for the derivative evaluation using cell-centre values avoiding the tedious reconstruction and Bi-Conjugate Gradient Stabilized (Bi-CGStab) method is used for the solution of the resulting system of linear equations. Combination of unstructured finite volume method along with the Bi-CGStab solver is first proved by applying it to the solution of an unsteady 3D convection diffusion equation. A Taylor based upwind scheme similar to that of Taylor Galerkin approach is used. This gives second order accuracy and results in a natural upwind term. After the Taylor series application the results are cast into the general divergence form so that the finite volume method can be applied directly. The stability of the solution is tried for various peclet numbers and found to be robust. The methodology is then extended to 3D Navier Stokes equations and the code is validated for the lid-driven cavity flow. The implicit solutions obtained for the Navier Stokes equation using Bi-CGStab method is found to save considerable amount of computation time
Keywords |
| Unstructured, Finite Volume Method, Unsteady, Fluid flow, Bi-CGStab method. |
INTRODUCTION |
| The fluid flow problems play a significant role in predicting and understanding the flow pattern in different flow processes. The various methods of analysis used are Experimental, Analytical and Numerical. Though experimental analyses offer the best results, it is often costly and constrained by physical restrictions. Limited amount of information on limited number of specific conditions and instrumentation errors limit the application of experimental analysis. In analytical method, most of the governing equations are non-linear and it becomes too tedious to solve and may also require drastic simplifications. Owing to these inherent problems in experimental and analytical methods, numerical computation plays a crucial role. The numerical simulation of an industrial system on computer involves mathematical representation of the physical processes undergone by the various components of the system, by a set of equations (usually differential equations) transformed to set of simultaneous algebraic equations, which are in turn solved as a set of simultaneous algebraic equations. With the advancements in Computational Fluid Dynamics, numerical techniques have become more powerful as compared to the other two techniques. The numerical simulations are becoming increasingly cheaper and more effective with the added advantage of its ability to predict far beyond experimental insight. It is possible to see simultaneously the effect of various parameters on the behaviour of the system since the speed of computing is very high. A large variety of problems with different levels of complexity can be simulated on computer. There are mainly three distinct streams of numerical solution techniques: finite difference, finite element and finite volume methods. In this work, finite volume method is used for obtaining the solution. Finite volume method is the name given to the technique by which the integral formulations of the conservation laws are discretized directly in the physical space. The clear relationship between the numerical algorithms and underlying physical conservation principle forms one of the major attractions of the finite volume method which makes the concept very simple to understand than finite element and finite difference methods. The application of finite element and finite volume methods to the governing partial differential equation results in a large system of simultaneous equations especially for 3D problems. Efficient solution of these equations can considerably save the computation time. Iterative solution techniques like conjugate gradient and bi-conjugate gradient methods are increasingly becoming more and more popular in finite element method as they avoid the assembly of large matrices and allow for an efficient element-byelement solution. It has been demonstrated that the above techniques save considerable amount of memory and computing time. The element-by-element solution methodology applied in finite element method is directly adopted for the implicit time integration of the ordinary differential equations resulting from the application of the unstructured finite volume method to the convection diffusion equation. |
| In this project work, the aim is to analyze the fluid flow, by using the three-dimensional unstructured finite volume method applying biconjugate gradient stabilized method [3] as the numerical solution tool. The work deals with the unstructured finite volume method for the analysis because the method takes full advantages of an arbitrary mesh, where large number of options are open for the definition of the control volumes around which the conservation laws are expressed. In addition, by the direct discretization of the integral form of the conservation laws we can ensure that the basic quantities mass, momentum and energy will remain conserved at discrete level. In this work, tetrahedron elements are used for the space discretization because of its flexibility in meshing and will give very good results for all complex geometries. |
II. MODELLING AND FORMULATION OF CONVECTION DIFFUSION EQUATION |
| A. Mathematical modelling |
| All of Computational Fluid Dynamics (CFD) in one form or the other is based on the fundamental governing equations of fluid dynamics – the continuity, momentum and energy equations. They are the mathematical statements of three fundamental physical principles upon which all of fluid dynamics is based: Mass is conserved, Newton’s second law and Energy is conserved. These fundamental principles can be expressed in terms of mathematical equation, which in their general form are usually partial differential equations. CFD determines a numerical solution to the governing equation of fluid flow while advancing the solution through space and time to obtain a numerical description of the complete flow field of interest. The governing equations of fluid flow are described below. |
| 1) Mass conservation equation. |
| The mass conservation equation is given by, |
| Where, ρ is the density of the fluid, u, v and w are the velocity components along x, y and z respectively. It can be written in the following form also. |
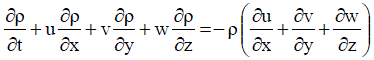 ....... (2) ....... (2) |
| For incompressible flows, ρ being constant, the above equation reduces to the form |
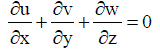 ....... (3) ....... (3) |
| And the rest of the equations are written directly for incompressible flows with constant property assumptions. |
| 2) Momentum conservation equation |
| X-Momentum equation is given by, |
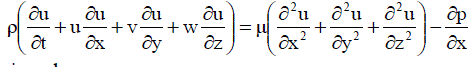 ....... (4) ....... (4) |
| Y-Momentum equation is given by, |
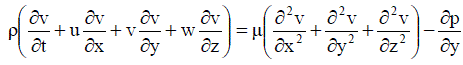 ....... (5) ....... (5) |
| Z-Momentum equation is given by, |
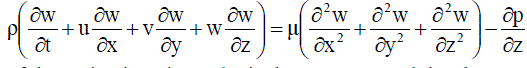 ....... (6) ....... (6) |
Where, μ is the coefficient of dynamic viscosity and p is the pressure; and the above equations can be further simplified by defining 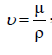 the kinematic viscosity. the kinematic viscosity. |
| 3) Energy conservation equation. |
| The energy conservation equation is given by, |
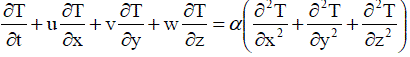 ....... (7) ....... (7) |
Where, T is the temperature and α is the thermal diffusivity defining 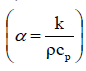 , where k is the thermal conductivity and cp the specific heat at constant pressure. The above equations can be cast into a general form as follows, , where k is the thermal conductivity and cp the specific heat at constant pressure. The above equations can be cast into a general form as follows, |
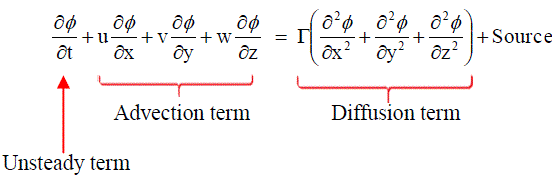 ....... (8) ....... (8) |
Which can be written in a more compact form as 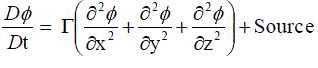 ....... (9) ....... (9) |
| Where ÃÂÃâ is an exchange coefficient defined below for different definition of ÃÂÃâ¢. This is typical of convection-diffusion equation. Here the values of the variables will be as follows (Table 1) |
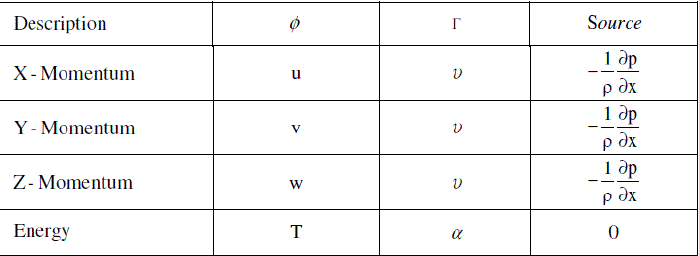 |
| Table 1. The values of the variables of convection diffusion equation |
| As all the governing equations follow the general convection diffusion equation, a solution methodology developed for this equation can be uniformly applied for all the equations. The Taylor-Galerkin method has been successfully used for the finite element solution of convection-diffusion equations for both 2D and 3D problems. On similar lines the method is extended for unstructured finite volume solution of the 3D convection diffusion equation as described in the next section. |
| 4) Taylor based upwind scheme |
| Standard central difference schemes when applied to the solution of the above equation usually results in numerical oscillations when the peclet number (pe = uL/ÃÂÃâ) is above 2. To overcome this difficulty, various upwind schemes have been suggested. One of the popular upwind scheme in finite element method is the Taylor Galerkin method. In the frame work of Taylor Galerkin method, the solution is achieved by first approximating the time derivative by means of Taylor series expansion and after some algebraic manipulation the finite element method is applied. The same methodology is adopted and finite element method is replaced by unstructured finite volume method as described below. |
| The general form of the governing equations is |
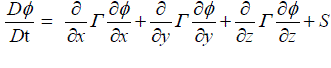 ....... (10) ....... (10) |
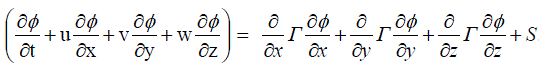 ....... (11) ....... (11) |
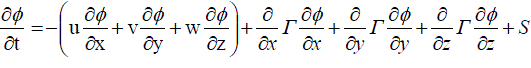 ....... (12) ....... (12) |
| From Taylor series expansion, |
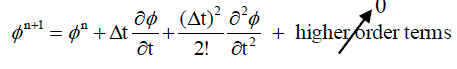 ....... (13) ....... (13) |
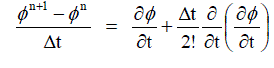 ....... (14) ....... (14) |
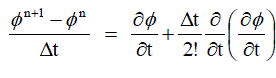 ....... (15) ....... (15) |
| Substituting the value of |
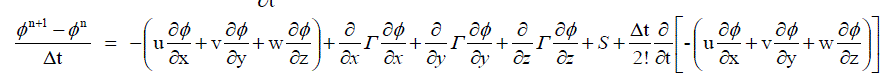 ....... (16) ....... (16) |
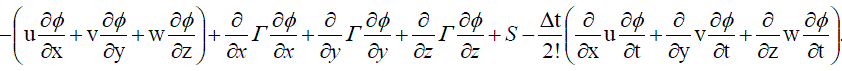 ....... (17) ....... (17) |
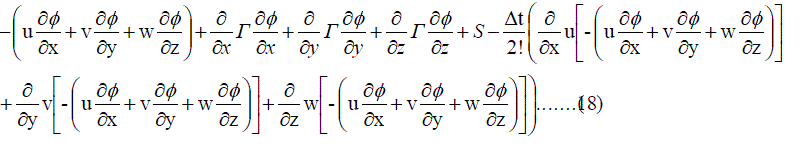 |
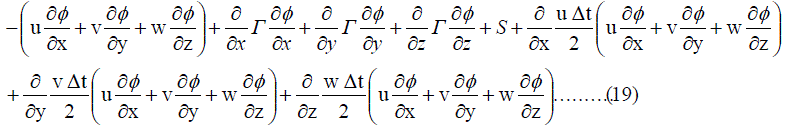 |
| The above equation results in second order time accuracy as well as a natural upwind term |
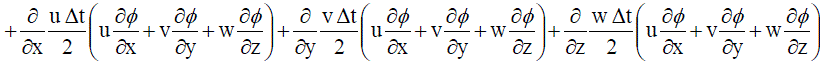 ...... (20) ...... (20) |
| which stabilizes the solution for higher peclet numbers and is a function of time step Δt and velocities u, v and w. The derivatives in x, y and z in the above equation can be clubbed together to get the following form |
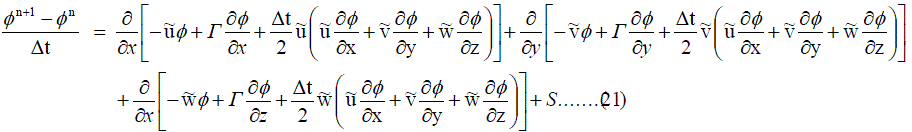 |
| Now the above equation is reduced into a divergence form |
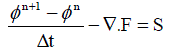 ..... (22) ..... (22) |
| So, the finite volume formulation can be applied. |
| B. Finite volume formulation |
| Integrating equation (22) over the control volume V, |
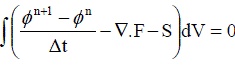 ..... (23) ..... (23) |
| Applying Greens theorem and converting the volume integral to surface integral we have, for an elemental control volume Vi of ith element, |
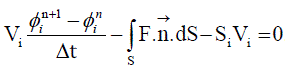 ... (24) ... (24) |
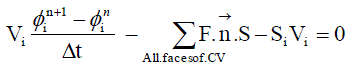 ... (25) ... (25) |
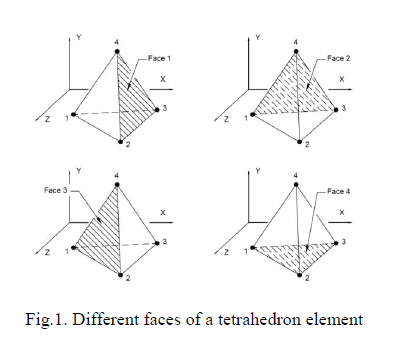
| Since the tetrahedron has4 faces, |
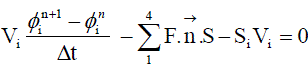 ... (26) ... (26) |
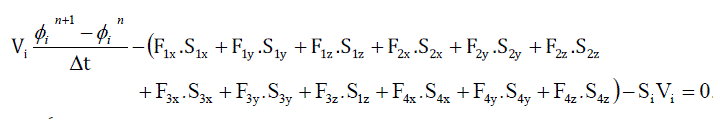 .. (27) .. (27) |
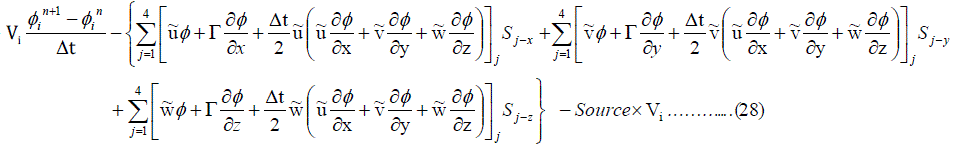 |
| Where, S1x, S1y, S1z are the projections of face-1 area (S1) along x,y,z. S2x, S2y, S2z are the projections of face-2 area (S2) along x,y,z. S3x, S3y, S3z are the projections of face-3 area (S3) along x,y,z. S4x, S4y, S4z are the projections of face-4 area (S4) along x,y,z. The different faces of tetrahedron are shown in figure 1. The convention used is the face opposite to node 1 is named as face 1 and so on |
 |
| The above equation can be written as |
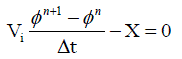 .......... (29) .......... (29) |
| The above equation can be solved implicitly. For Impicit sheme X is evaluated for ÃÂÃâ¢n+1 i.e for the value at the next time step (t+Δt), |
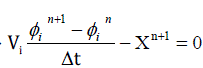 .......... (30) .......... (30) |
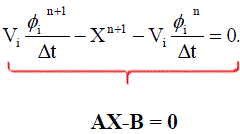 .......... (31) .......... (31) |
| Once the computation of the fluxes over all the faces is completed, the aove equation reduces to a form AX-B=0 and this can be solved using any of the iterative methods. Here we use Bi-CGStab method. The computation of fluxes over the four faces requires the evaluation of u, v, w and ÃÂÃ⢠and its derivatives in x, y and z direction. The primitive variables are averaged between the elemental values on either side of the face and the derivative evaluation is explained as given below. The present method of derivative evaluation totally avoids the reconstruction of variables from elemental value to nodal values. |
| 1) Evaluation of derivatives |
| The derivatives are calculated at the faces of tetrahedron using Taylor series based least square method. Let “ïÃÂæ ” be the variable ( u,v,w or T ) and the Taylor series is given by |
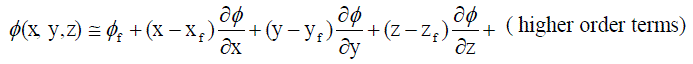 .......... (32) .......... (32) |
| Higher order terms are neglected since the value is small. If the values of the function are known at a points or neighbors (i = 1 to n, n = total number of neighbors and the subscript “ f “ represents the face center value), we can approximate the derivatives of the function at the reference node (face centered value) by solving a system of linear equations. For such an approximation we select the points i = 1 to n, we are in the immediate neighborhood of the reference point. The above equation can be written in the form, |
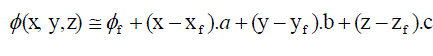 .......... (33) .......... (33) |
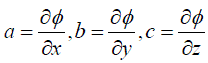 .......... (34) .......... (34) |
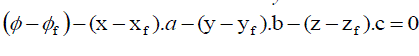 .......... (35) .......... (35) |
| The above equation is of the form |
| The derivative evaluation for each face is to be unique as the face is shared by two elements on either side having two cell-centre values of the variable which is insufficient to compute the derivatives. One option is to reconstruct the three nodal values of the variables from the neighbouring cell centre values and then use them along with the two cell centre values to get the derivatives. This is quite time and memory consuming process. Hence an efficient and unique derivative evaluation directly from the cell centre values is developed. As the face is shared by two elements, we have the cell centre values of all the four neighbours of each element (see figure 2). As we have now three unknowns (a,b,c) and eight equations, a least square based methodology is used to determine the derivatives. The Least square method of evaluating gradients is as follows, |
 ..........(37) ..........(37) |
| Squaring on both sides we get, |
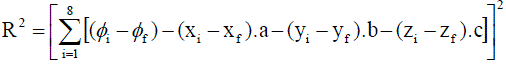 ..........(38) ..........(38) |
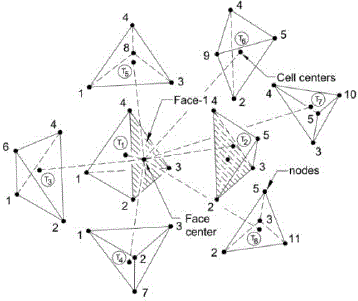 |
| Fig.2. Cell center values used for the evaluation of the gradient through faces |
| To evaluate a,b,c, differentiate R2 w.r.t a,b,c and equate to zero. i.e, |
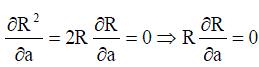 .........(39) .........(39) |
| Differentiating w.r.to “ a “ we get |
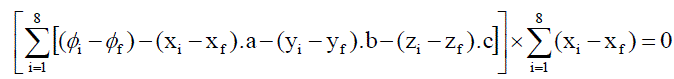 .........(40) .........(40) |
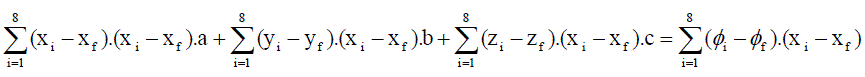 .........(41) .........(41) |
Now differentiating w.r.t “ b “ we get, 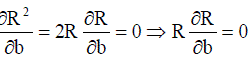 .........(42) .........(42) |
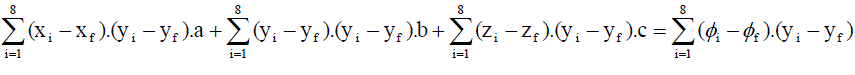 .........(43) .........(43) |
And finally differentiating w.r.t “ c “ we get, 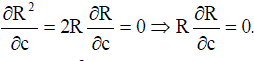 ........(44) ........(44) |
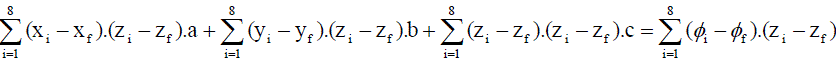 ........(45) ........(45) |
| From above three equations we can get a,b,c. The above set of equations can be written in matrix form as follows |
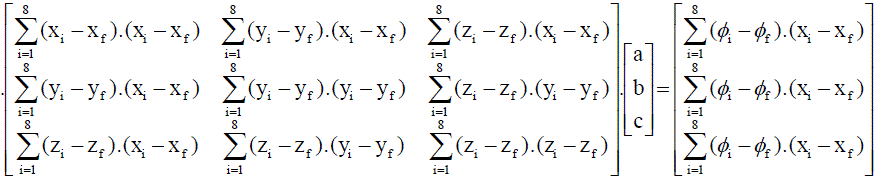 ........(46) ........(46) |
| To improve the accuracy, the weights have been incorporated for the evaluation of derivatives. i.e by considering the distance from eight cell center values. The above matrix can be solved for a,b,c using crammers rule. Now equation (31) is solved using Bi-CGStab method. The algorithm for Bi-CGStab this method is given below, |
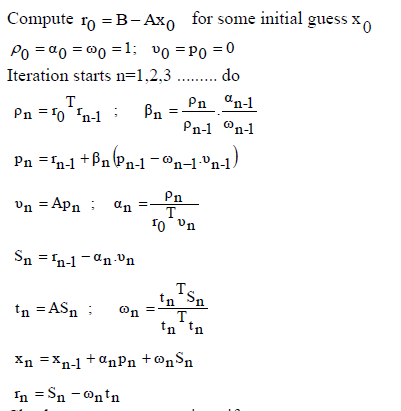 |
| Check convergence; continue if necessary End do |
III. VALIDATION FOR CONVECTION DIFFUSION PROBLEM |
| Now for the validation of convection diffusion equation, replacing ÃÂÃ⢠as T, ÃÂÃâas α and Source as 0 in (28), the equation reduces to |
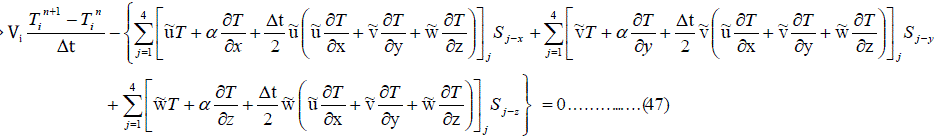 |
| With the evaluation primitive variables and their derivatives, the fluxes on each of the four faces of the tetrahedron can be evaluated. Multiplied by the projected surface areas and summing up gives the residue for each element. This results in a system of ordinary differential equation in time for the convection diffusion equation (ie. ÃÂÃ⢠= T, ÃÂÃâ= α and Source = 0). For the evaluation of derivatives see the section above. The above equation can be written as |
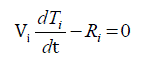 ....(48) ....(48) |
| Explicit and implicit time stepping schemes can be used for the integration of these system of ordinary differential equations. Explicit schemes schemes are conditionally stable and many times the time steps become extremely small for many practical problems. The advantage is that the residue, Ri, can be explicitly evaluated from the values of the primitive variables known at the previous time step. Though the implicit schemes are unconditionally stable, the residues are to be computed on the current time level which involves the solution of the matrix system which is nonsymmetric. The iterative solution technique, Biconjugate Gradient Stabilized method can be used effectively here as it can be modified as an element-by-element solver. |
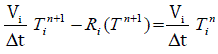 ....(49) ....(49) |
| The main advantage of the BiCGStab solver is that it requires always the residue B-AX or the column vector ïÃÂÃâºAïÃÂÃÂïÃÂûXïÃÂý which totally avoids the assembly of matrix ïÃÂÃâºAïÃÂÃÂ. For iterative improvement of the solution, the L.H.S of the above equation is computedwith different values of unknown T and the solution proceeds to make LHS – RHS to zero. It is reported that the convergence of BiCGStab method is fast. Hence this solver is used to the present effort to solve the system of equations resulting from the application of unstructured finite volume method to the 3D unsteady convection diffusion equation. The above equation can be solved implicitly as explained in the earlier section and the results are as follows. |
| To test the efficiency and accuracy of the code, a standard test case of a one dimensional convection-diffusion problem for various peclet numbers is tried. A rectangular computational domain was considered, as shown below. The computational domain (74mm × 5mm × 5mm) is discretised using unstructured tetrahedron elements having 56187 elements and 12020 nodes as shown in figure 3. The aspect ratio of the tetrahedral elements were kept close to one. The thermo-physical properties used are, Density, ρ = 2702 kg/m3, Specific heat, Cp= 903 J/kgK, Conductivity, Kx , Ky , Kz = 237 W/ mK, Tinit = 300 K, T0 = 350 K, at z = 0, TL = 300 K, at z = 74mm |
 |
| Fig.3. Rectangular computational domain |
| The problem analyzed earlier using conventional finite element methods had resulted in large oscillation for peclet number of 2 and above. As peclet number is the ratio of heat transfer by convection to heat transfer by conduction, for most practical problems the peclet number is seen to be higher than 2. Hence the code has checked for a wide range of peclet numbers. The steady state solution for different peclet numbers in steps from 0 to 600 are obtained and are shown in figure 6. Figure 4 a) shows the temperature distribution along the centre line of the rectangular slab for peclet number zero. Here u = v = w = 0 and the equation transforms to a pure conduction problem with a resulting linear temperature profile from 350K to 300K from hot end to cold end. The Bi-CGStab is able to achieve an error of 1.0e-21 in 714 iterations. Figure 4 b) shows the steady state temperature distribution for peclet number 2. This is achieved by increasing the axial velocity u = 0.002625 m/s, keeping v and w zero. Due to the effect of axial velocity along with conduction, the influence of heat transport by convection is also visible in the temperature profile. The Bi-CGStab is able to achieve an error of 1.0e-21 in 889 iterations. |
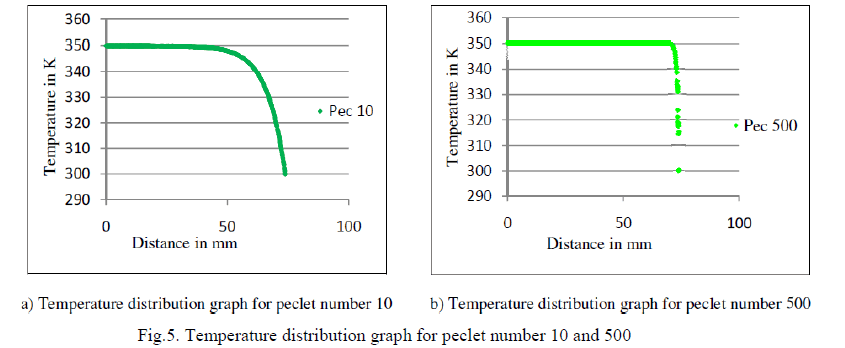
| Peclet number is further increased to 10 by increasing the axial velocity u=0.013126 m/s keeping all other parameters the same. The steady state temperature distribution is shown in figure 5 a). Heat transport by convection makes the temperature constant upto about 40mm from the high temperature end. |
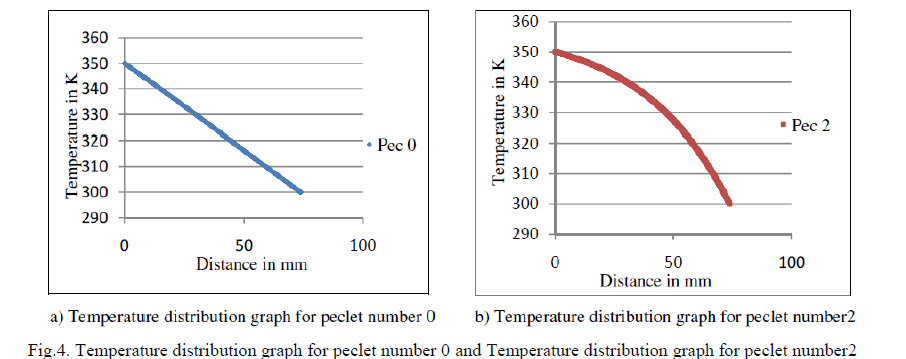 |
| The temperature distribution is absolutely oscillation free confirming the effectiveness of the natural upwind term in the present method. The Bi-CGStab is able to achieve an error of 1.0e-21 in 932 iterations. Peclet number is further increased to 500 and the corresponding axial velocity is u=0.6563 m/s. The temperature distribution is shown in figure 5 b) and no oscillations are seen in the temperature profile. Temperature is constant almost up to the end of the slab and the convection is totally dominating the heat transfer. The Bi-CGStab is able to achieve an error of 1.0e-21 in 13914 iterations. |
 |
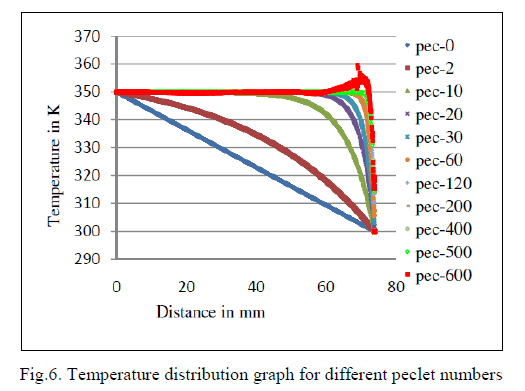 |
| Figure 6 shows the steady state temperature distributions for different peclet numbers. The temperature distribution is absolutely oscillation free till for a peclet number 500. Slight oscillation starts for a peclet number 600. A comparison of the results of the present code with Analytical result is carried out for peclect number zero. The unsteady temperature distribution at t=10 seconds is compared and is shown in figure 7 a). The results match very well. The tecplot contour showing temperature distribution at 10 seconds is shown in figure 7 b). The thermo-physical properties used for validation by conduction are, Density, ρ = 1000 kg/m3, Specific heat, Cp= 2000 J/kgK, Conductivity, Kx , Ky , Kz = 20 W/ mK Tinit = 300 K, T0 = 500 K, at z = 0, TL = 300 K, at z = 74mm, Initial velocities (u0, v0, and w0) = 0 |
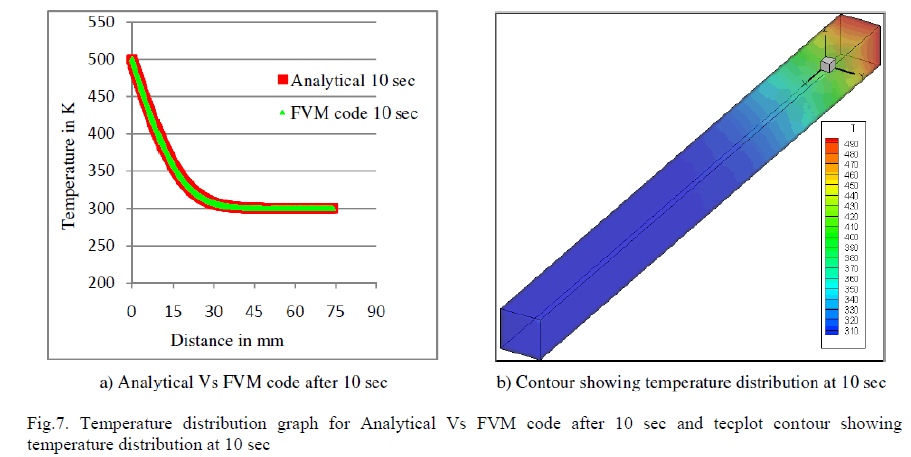 |
| The stability of the solution is tried for various peclet numbers and the above result shows that the developed code is robust and accurate to handle effectively unsteady nonlinear convection diffusion problems. The code shows good result without oscillation even for a peclet number 500. So the code is extended to Navier Stoke equation as explained in the next section. |
IV. EXTENSION TO NAVIER STOKES EQUATION |
| The stability of the solution of convection diffusion equation is tried for various peclet numbers and found to be robust. The methodology is then extended to 3D Navier Stokes equations and applied for the solution of a lid-driven cavity problem. |
| A. Governing equations |
The flow field analysis of unsteady laminar incompressible flows needs the solution of the Navier-Stokes equations. The momentum equations in x, y and z directions are in the form of the convection diffusion equation by replacing ÃÂÃ⢠by u, v and w, ÃÂÃâ by ÃÅ Ãâ¹ and S by 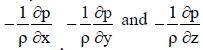 as follows. as follows. |
| General form of convection diffusion equation is |
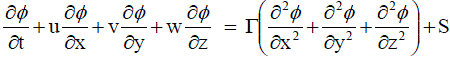 ……….. (51) ……….. (51) |
| Then, X-Momentum equation is given by |
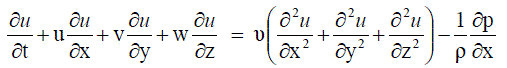 ……….. (52) ……….. (52) |
| Y-Momentum equation is given by |
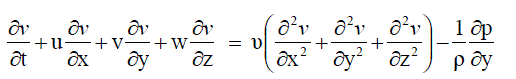 ……….. (53) ……….. (53) |
| Z-Momentum equation is given by |
 ……….. (54) ……….. (54) |
| Application of the numerical method described in the previous session results in the following equation |
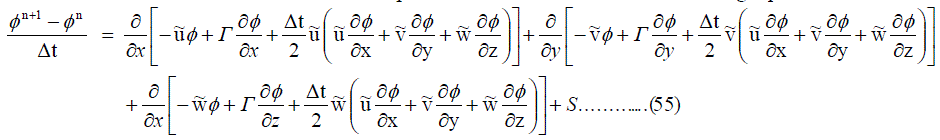 |
| y espectivel v and w r lues of u, revious va are the p w ~ and v ~ , u ~ Where, |
 |
| X – Momentum equation is given by |
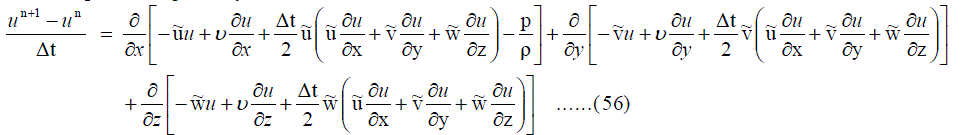 |
| Y – Momentum equation is given by |
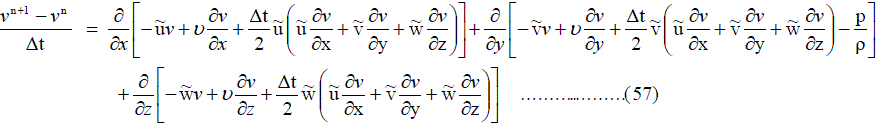 |
| Z – Momentum equation is given by |
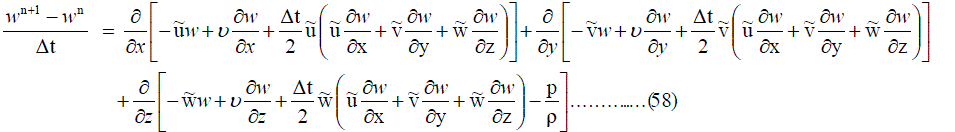 |
Since these equations are in a divergence form,  finite volume formulation can be applied. finite volume formulation can be applied. |
| The mass conservation equation is |
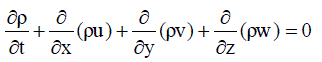 ……….. (59) ……….. (59) |
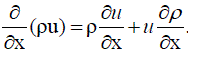 ……….. (60) ……….. (60) |
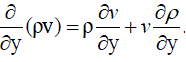 ……….. (61) ……….. (61) |
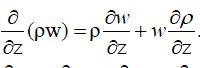 ……….. (62) ……….. (62) |
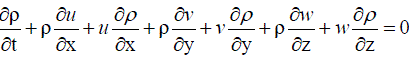 ……….. (63) ……….. (63) |
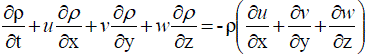 ……….. (64) ……….. (64) |
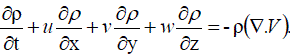 ……….. (65) ……….. (65) |
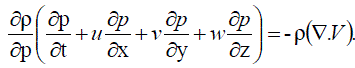 ……….. (66) ……….. (66) |
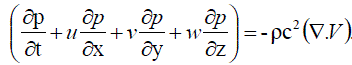 ……….. (67) ……….. (67) |
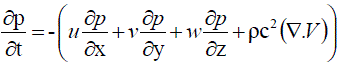 ……….. (68) ……….. (68) |
| From Taylor series expansion, |
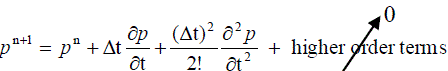 ……….. (69) ……….. (69) |
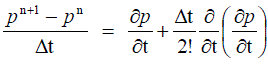 ……….. (70) ……….. (70) |
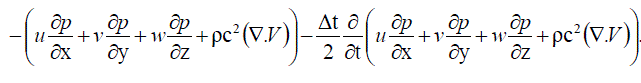 ……….. (71) ……….. (71) |
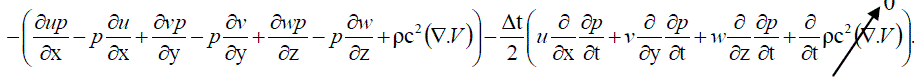 ……….. (72) ……….. (72) |
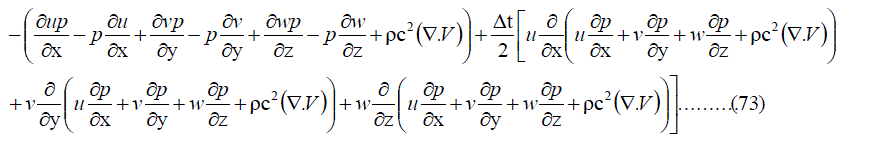 |
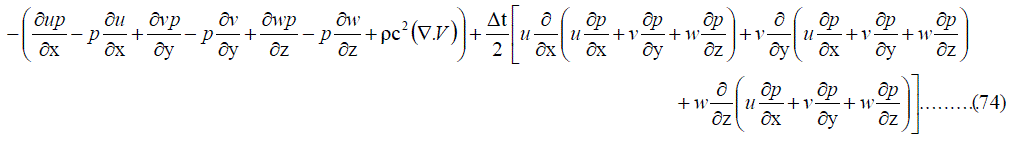 |
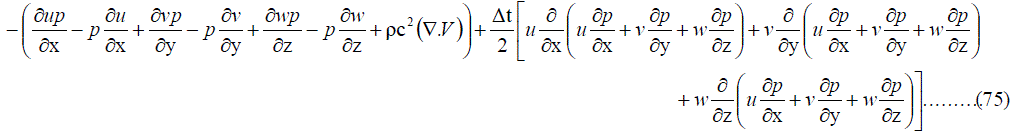 |
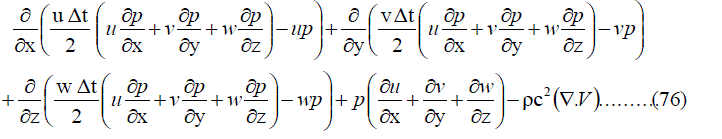 |
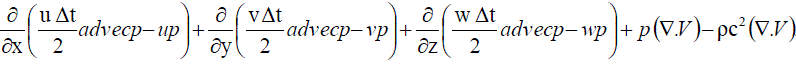 …….. (77) …….. (77) |
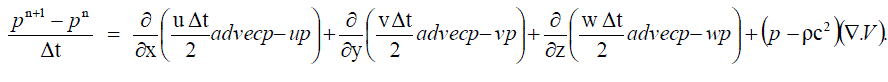 …….. (78) …….. (78) |
Where, 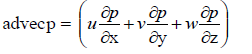 |
Now the mass conservation equation is also reduced into a divergence form 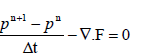 |
| So, the finite volume formulation can be applied. After applying finite volume formulation as explained in section II B, the above momentum and mass conservation equations are reduced as follows. |
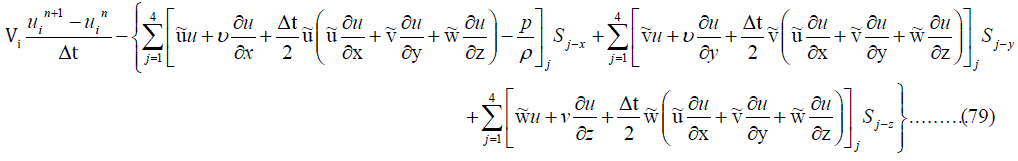 |
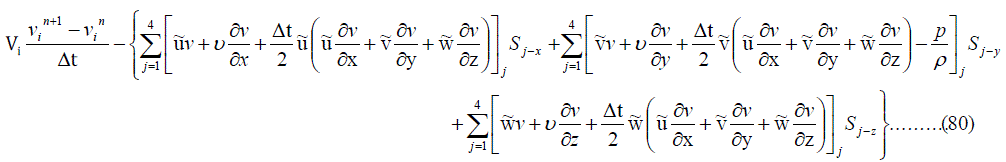 |
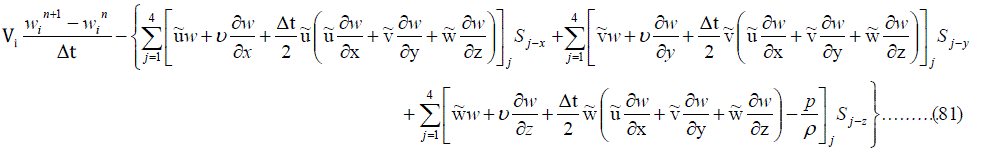 |
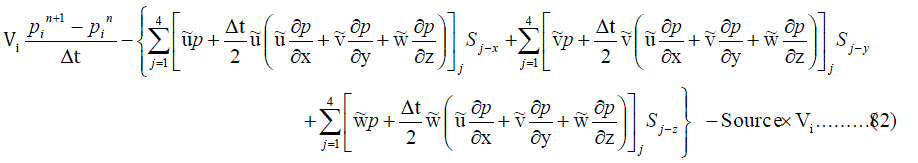 |
| Once the computation of the fluxes over all the faces is completed, the aove equation reduces to a form AX – B = 0 and this can be solved using any of the iterative methods. Here we use Bi-CGStab method. |
| B. Validation using lid driven cavity flow |
| 1) Lid driven cavity flow. |
| The lid driven cavity problem is one of the standards used to test new computational schemes. It may be worthwhile to briefly mention why cavity flows are important. In no other class of flows are the boundary conditions so unambiguous. As a consequence driven cavity flows offer an ideal frame work in which meaningful and detailed comparisons can be made between results obtained by numerical simulation, experimental analysis and theoretically as well. Another great advantage of this class of flows is that the flow domain is not changed when the Reynolds number is increased. This helps for investigations over the whole range of Reynolds numbers, 0 < Re < infinity. Thirdly driven cavity flows exhibit almost all phenomena that can possibly occur in incompressible flows, like eddies, secondary flows, complex three dimensional patterns, instabilities, transition and turbulence. |
| The accuracy and efficiency of the algorithm presented have been verified by solving lid driven cavity flow problem. Evaluating the results obtained from the numerical simulation of the different cavity configuration require careful consideration. The issue that is central to the analysis is the question of the numerical solution reaching a steady state for a given Reynolds number. The steady state solution is important for two reasons. The first reason is that it allows comparison of the centre line velocity profile obtained from the proposed algorithm with center line velocity profiles reported by other investigators. Secondly, a steady state solution allows the comparison of centerline velocity profiles obtained from two and three dimensional representation of the same physical problems. |
| 2) Details of the problem |
| The physical configuration of the lid driven cavity is that of a unit cubic cavity with rigid walls filled with a fluid. The fluid is set in motion by moving the top boundary (lid) in X-direction at a constant velocity. The top wall is moved in the positive x-direction with a velocity ulid, which is varied to simulate different Reynolds numbers. No-slip boundary condition is applied on the side walls and the bottom of the cavity. A time-dependent version of the classical steadystate problem as discussed earlier is considered by assuming that the fluid is initially at rest and that the driving wall is impulsively set into motion at t=0 with constant velocity, ulid. The moving lid surface is open to the atmosphere and the other three boundaries have zero normal pressure gradients. |
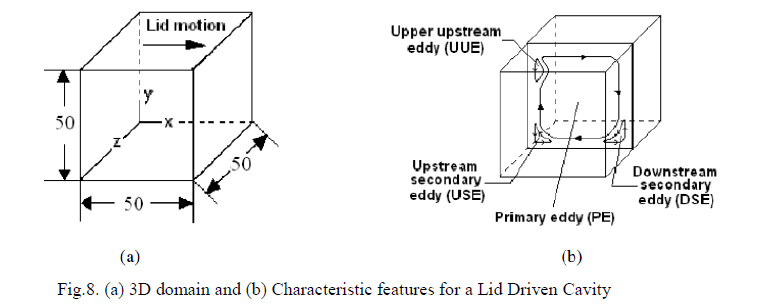 |
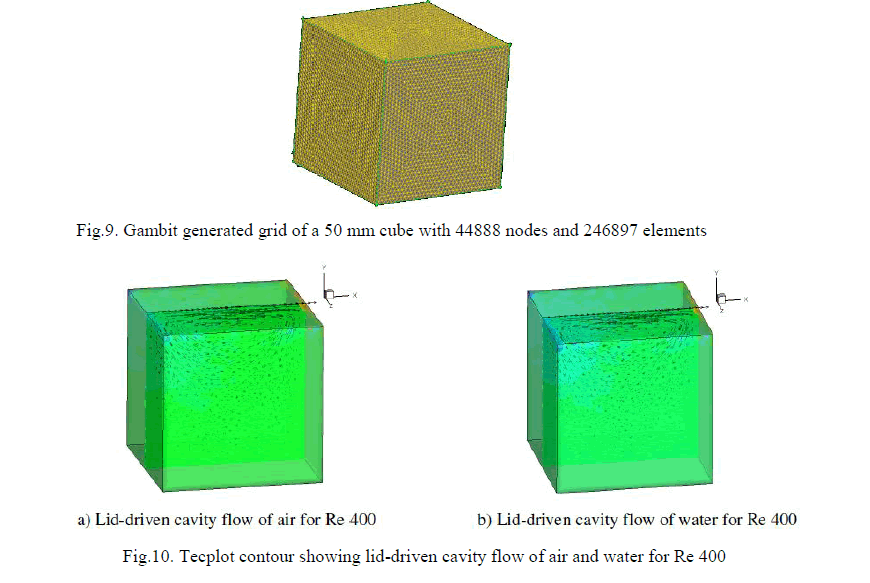
| The flow field will depend not only on the Reynolds number but also on the depth of the cavity. The problem considered is shown in figure 8 (a) and refers to the three-dimensional flow in a cubic cavity of sides 50mm. The basic characteristics of the boundary driven flow are shown in figure 8 (b). The initial conditions are: u(x, y, z, t=0) = u0(x, y, z), v(x, y, z, t=0) = v0(x, y, z) = 0, w(x, y, z, t=0) = w0(x, y, z) = 0 P(x, y, z, t=0) = P0(x, y, z) = 1bar The values u0 are 0.008m/s and 0.02m/s (By the relation u=(Re*μ)/(ρ*y) for Reynolds numbers 400 and 1000 respectively. The boundary conditions are: At x=0 & x=0.05m, u=v=w=0 (No Slip B.C at solid walls), At z=0 & z=0.05m, u=v=w=0 (No Slip B.C at solid walls), At y=0, u=v=w=0 (No Slip B.C at solid walls), At y=0.05m, u=Reμ/ρy, v=w=0 For validation of the code, water and air are taken as the fluids. The values of different properties of water and air considered initially are: For water, Density, ρ=1000 kg/m3, Viscosity, μ=1.0e-3Ns/m2 For air, Density, ρ=1.0 kg/m3, Viscosity, μ=1.0e-5Ns/m2 The physical domain, 50 mm cube is discretized by using tetrahedron elements. The mesh contains 44888 nodes and 246897 elements with a spacing of 1.5 mm. The grid generated in Gambit is shown in figure 9. For grid sensitivity study, another grid is generated with a spacing of 2 mm which gives 18966 nodes and 100686 elements. |
 |
| 3) Lid driven cavity flow. |
| The code is validated for laminar flow with Reynolds number 400. Results are presented as velocity vector diagram. The steady state is assumed to be reached when the difference between the solutions at two successive time steps is less than the prescribed tolerance of 10-10. During each time step the residual has been brought down to the order of which ensures that the corresponding discrete divergence of the velocity for the whole domain reduces nearly to machine zero. Grid sensitivity study has been conducted by meshing the domain in to double of the original, which also shows the same result. The above figures 10 a) and 10 b) show the velocity vector plot for Reynolds number 400. The results are qualitatively matching with the published results [8]. |
V. CONCLUSION |
| A Taylor based unstructured finite volume method (sequel to the Taylor-Galerkin finite element method) is developed for the solution of the unsteady three dimensional convection diffusion equation. An implicit time stepping method is adopted and the resulting system of algebraic equations are solved using an efficient Bi-Conjugate Gradient Stabilized (Bi-CGStab) solver. A Least square based methodology is used for the derivative evaluation using cell-centre values avoiding the tedious reconstruction. Using tetrahedral elements for the space discretization, a three dimensional convection diffusion equation is solved for various Peclet numbers and the stability and accuracy of the solution technique is demonstrated. The methodology is further extended to the solution of the incompressible Navier-Stokes equations and applied for the solution of a lid-driven cavity problem. The combination of unstructured finite volume and the Bi-Conjugate Gradient Stabilized solver results in saving considerable amount of computing time. |
ACKNOWLEDGMENT |
| I express my sincere indebtedness to Prof. C.P. Muhammad, HOD, Dept. of Mechanical Engineering., MES College of Engineering, Kuttippuram for giving me this opportunity to undertake the Project work as part of my study. I thank Mr. Ramarajan A, Asst. Prof. of Dept. of Mechanical Engineering for his valuable guidance and suggestions. I express my sincere gratitude to Dr.T. Jayachandran, Group Director, Advanced Propulsion Research Group, Vikram Sarabhai Space Center, Trivandrum for providing the guiding light throughout the duration of the work. He constantly supplied with me valuable inputs and guidance whenever required. I thank him for providing me the opportunity to work at the FMTD computational lab. I also thank all the other members of the FMTD, who have helped me in one way or the other during my stay. I take this opportunity to extent my sincere thanks to all the faculty members of the Dept. of Mechanical Engg. And to Dr. Vijayalakshmi Menon R, Asst. Prof., Dept. of Mathematics, MES College of Engineering, Kuttippuram for her valuable guidance. |