A Fuzzy Based Modeling for Assessment of Soil Degradation Due to E-Wastes

Abstract

All discarded wastes generated from electrical and electronic products are known collectively as e-waste. Out of all kinds of wastes that directly dispose of in the landfill, e-wastes are now most rapidly increasing sources of wastes in the world even though various recycling and reusable efforts are given to minimize the volume of it. In most of the city, sanitary landfill are not practiced rather wastes are dumping crudely in open landfill[7]. As a result soil gets highly contaminated due to the presence of lead, mercury, cadmium and other toxic substances in the e-wastes. At present no scientific tool or methods are available to an engineer to asses the quantification of soil degradation of a landfill except the process of Environmental Impact Assessment (EIA)[5,6].But EIA is a prediction method where an expert has certainly a limitation of knowledge or intellectual functionaries for his perception. Because the data available around the periphery of landfill are not always crisp or precise rather linguistic and hedges viz. “good”, “very good”, “bad”, “low”, “high”, “severe”, “less”, etc. to list a few only out of infinity. Evaluation of many objects here is not possible with numerical valued descriptions because uncertainty is an integral part of prediction of any such data[1]. This paper deals with a methodology of “vague fuzzy EIA‟ for assessment of soil degradation with degree of certainty.

Keywords

Attributes, EIA, E-waste, Fuzzy set, Mean vague value, Vague set etc.

INTRODUCTION

The soil degradation has increased dramatically with rapid growth of industries with advancements in the field of electronic and electrical technologies. All the e-waste like discarded computers, television sets, cell phones, video & audio equipments, electrical lamps, circuit boards, chips resistors & semiconductors, relay, switches, etc if are not properly dispose in the sanitary landfill, then leachate generated as a result of percolation of rain water and squeezing of e-wastes itself posing a great threat in the surrounding soil structure of the landfill [3]. Each type of e-waste contains heavy metals like circuit board contain lead and cadmium, batteries contain cadmium, cathode ray tubes contain lead oxide, fluorescent lamps contain mercury, etc. The estimation of total quantity of e-wastes in a city is very difficult because all the sources of generation points are not known always unless or until it is not finally discarded by the users. Till day no scientific collection system are exist for safe disposal of e-wastes and as a result scavengers or the persons those are handling e-wastes daily are becoming unknowing fully at risk of death. Similarly the leachate generated from e-wastes is highly contaminated that ultimately degrades the essential nutrients of soil like nitrate, phosphorus, potassium, calcium, magnesium etc. Thus to protect the soil from anticipated toxicity of leachate, an EIA is very essential to conduct by the soil expert before finalization of any major project nearby landfill site. In EIA a systematic analysis are carried out using information or data collected from different sources and predict the environmental consequences on the project [2]. But this kind of prediction involves uncertainty that influence the actual result of EIA. Generally there are two types of uncertainty associated with EIA that associated with the process and that associated with predictions. The accuracy of predictions is dependent on a variety of factors such as lack of precise data or lack of precise knowledge. Most of the judgments are done by human being or intelligent agent who has certainly a limitation of knowledge or intellectual functionaries to tackle the uncertainty. But a soil expert can feel much more confidence and can better guess a degree of belongingness or a degree of non-belongingness independently within the interval [1,0] instead of defining the EIA result as „very polluted‟ or „extremely degraded‟ or „not degraded‟ etc. At present fuzzy logic of Prof. Latfi Zadeh [8] has proved it‟s tremendous power worldwide to tackle the uncertainty and vaugness involved in such real life problems. In this paper „Vague Fuzzy EIA‟ tool has been introduced for assessment of soil degradation of a landfill with degree of certainty.

PRELIMINARIES

In this chapter some preliminaries are discussed which will be very useful in modelling of vague fuzzy EIA tool. Fuzzy Sets (FS) and Fuzzy Logic [8] : The concept of uncertainty has a vital role in the solution of our daily life problems and thus needs to tackle it properly. Prof. Latfi Zadeh first laid the foundation of fuzzy set theory in 1965 by generalization of ordinary crisp set theory. According to his concept, when a statement is completely true then the membership value is 1 and when a statement is completely false the membership value is 0 and when the statement is partially true and partially false then the membership value will be in between 0 and 1. Thus the membership function of a fuzzy sets can take any value form the closed interval [0,1]. It is expressed as the set of ordered pairs like A = { ( x1, A(x1) ), (x2, A(x2) ), ….. , (xn , A(xn) )}, where A(xi), is the grade of membership of element xi in set A. The greater value of A(xi), indicates greater the truthness of statement that „the element xi belongs to set A‟.

Vague Fuzzy Set (VFS) [4] : A vague set A in the universe of discourse U is characterized by two membership functions given by :-

(i) a truth membership function , t A : U → [0, 1], and

(ii) a false membership function , f A : U → [0, 1]

where tA(u) is a lower bound of the grade of membership of u derived from the „evidence for u‟, and fA(u) is a lower bound on the negation of u derived from the „evidence against u‟, and tA(u) + fA(u) ≤ 1. Thus the grade of membership of u in the vague set A is bounded by a subinterval [tA(u), 1- fA(u)] of [0,1]. This indicates that if the actual grade of membership is μ(u), then tA(u) ≤ μ(u) ≤ 1- fA(u). The vague set A is written as A = { < u, [tA(u), fA(u)] > : u  U }, where the interval [tA(u), 1- fA(u)] is called the vague value of u in A and is denoted by VA(u). For example, consider an universe U = {high pH, less BOD, less nitrate}. A vague set (VFS) A of U could be A = { < high pH, [.7,.2] >, < less BOD, [.3,.5] >., < less nitrate,[.4,.6]> }.

METHODOLOGY OF VAGUE FUZZY EIA

For better understanding the methodology of vague fuzzy EIA tool the following essential definitions are discussed below.

1. Attribute of the Assessment : The assessment is done by obtaining the expert‟s perception for certain prefixed attributes which are called the attributes of the assessment. For example, consider a project “ASSESSMENT OF SOIL DEGRADATION AROUND THE PERIPHERY OF e-WASTE LANDFILL SITE” , for which some relevant attributes could be “low Ph”, “high BOD5”, “ very high COD”, “low phosphorous”, “less nitrate”, “high potassium”, “good approach road”, “high alkalinity”, “very less chromium”, etc.

2. Universe of the Assessment : Collection of all attributes of the assessment is called the Universe of the Assessment. Let E = { x1, x2, x3,….. , xn } be a finite discrete universe of attribute xi , i = 1, 2, 3, …, n. Mean Vague Fuzzy Set : Let E be an universe and X be an VS of E. The mean vague value of the VS X is also a fuzzy set Y of E whose membership function μvs (x) given by

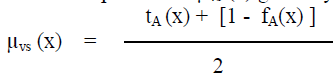3. Union of Mean Fuzzy Sets : If A and B are two mean fuzzy sets of universe U, then union of mean fuzzy sets A and B will be a fuzzy set X with the membership function μAB. Example: If A and B are two mean fuzzy sets such that A = {a/0.4, b/0.2, c/0.5, d/0.5} and B = {a/0.2, b/0.9, c/0.7, d/0.5}, then union fuzzy set X of mean fuzzy sets A and B will be X(μ AB) = {a/0.4, b/0.9, c/0.7, d/0.5}.

4. Weighted Averages of an Union Fuzzy Set : Let X be an union fuzzy set with membership function (x) of universe E. Suppose that to each element x  E, there is an associated weight Wx  R+ (set of all non-negative real numbers). Then the weighted average of the fuzzy set X is the non-negative number a (X) given by

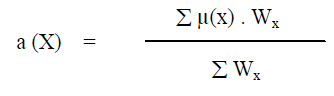5. Grading of Assessment Output

In Fuzzy-EIA modeling, evaluation of all attributes are done either based on their negative aspects (draw backs) or positive aspects. If negative aspects of all attributes are consider then grading of output results of Fuzzy-EIA could be proposed as below:

CASE STUDY

Let us consider the project “ASSESSMENT OF SOIL DEGRADATION AROUND THE PERIPHERY OF e-WASTE LANDFILL SITE”. Suppose for simplicity in presenting our methodology we consider only ten locations around the periphery of landfill as L1, L2, L3, L4,…L9 & L10 and select ten parameters as pH, BOD5, COD, phosphorus, nitrate, potassium, magnesium, alkalinity, chromium and lead. The lab test results of all these parameters for each location has been carried out in table-1 and we consider these data as a base line data for our main works.

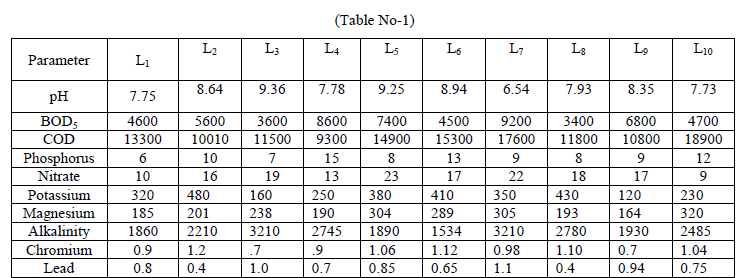In Fuzzy EIA modeling, attributes plays a main keys for assessment of the job. For making simplicity in the methodology of vague fuzzy EIA tool, we consider the following ten attributes (Drawbacks) out of many for each location of the landfill :-

x1 = high pH

x2 = high BOD5

x3 = high COD

x4 = high phosphorus

x5 = high nitrate

x6 = high potassium

x7 = high magnesium

x8 = high alkalinity

x9 = high chromium

x10 = high lead

Now the job is to assign the vague values of these attributes for all locations independently by obtaining views and perception from individual experts. All the vague values of any location will lead to an individual VFS of the universe U, where U = { x1, x2, x3, x4, x5, x6, x7, x8, x9, x10 }. Suppose for ten locations, the individual VFSs are designated as V1, V2, V3, V4, V5, V6, V7, V8, V9, V10 and the membership functions generated from the expert‟s views and perceptions for each VFS are described as :

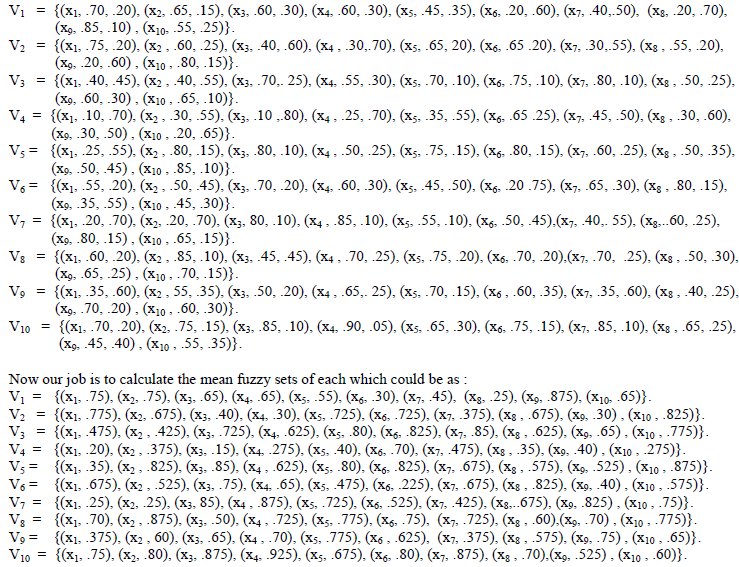For overall assessment of soil quality of the landfill, the union of all above fuzzy sets (as we consider the draw back of the attributes) will give the overall membership value of each attributes for the river. Thus the union fuzzy set X of the fuzzy sets V1, V2, V3, V4, V5, V6, V7, V8, V9, V10 will be

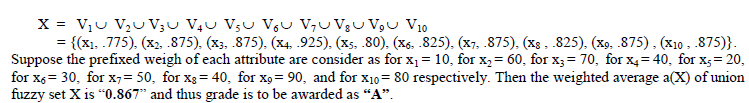Result : The soil condition of landfill is extremely degraded.

CONCLUSION

The vague fuzzy EIA tool can suitably be applied in assessment of soil degradation around the periphery of landfill. It has a great role to ascertain and verify the performance of a landfill concept with degree of certainty. The outcome results of such type of fuzzy modeling give more precise result to an engineer then any other tool available to him at present. It also help the solid waste management authority to compare all the landfills under his jurisdiction in respect of adverse soil degradation due to leachate generated and transmitted around the periphery of those landfills. The model can now claim an official status in international level because of it‟s powerful capacity to minimize the uncertainty faced by an engineer in his daily life in the field.

References

1. [1] Biswas, Srijit ., A fuzzy approach to Environmental Impact Assessment, published in the “Asian Journal. of Information Technology”, 4(1) : 35-39, 2005, Grace Publication Network-2005.
2. [2] Carter, Larry W., Environmental Impact Assessment, M. Graw Bill, New York, 1977.
3. [3] Chain, E.S and DeWalle, F.B., 1976, Sanitary landfill leachates and their treatments. “Journal of Envn. Engg. Div., ASCE”, 102(EE2) : pp 215- 239
4. [4] Gau, W.L., and Buehrer, D.J., 1993,”Vague Sets, IEE Transaction on System, Man and Cybernetics”, Vol-23, pp 610-614
5. [5] Gzogala, E., Rawlik, T.,1989, Modeling with a fuzzy controller with application to the control of biomedical process, Fuzzy sets and Systems, 31, pp 13-32
6. [6] ISRIC(1988), Guidelines for the general assessment of the status of human induced soil degradation, Working paper & Preprint 88/4, Wageningen [NL] : ISRIC
7. [7] Omar Al-Jarrah, Hani Abu- Qdais, “ Municipal solid waste landfill sitting using intelligent system”, “Elsevier- Waste Management, 26(2006), pp 299-306
8. [8] Zadeh. Latfi. A. Fuzzy sets, Info: and Control, 8(1965), pp 338-353