A New Approach for Image Fusion Based On Fast Discrete Curvelet Transform

Abstract

In recent years, image fusion is one of important prime method in image processing. Image fusion deals with creating an image in which all the objects are in focus. Thus it plays an important role to perform other tasks of image processing such as image segmentation, edge detection, stereo matching and image enhancement. To perform all these tasks several methods has been proposed. In this paper it is compared existing neural network based method with advanced discrete curve let method. In the result it is shown that the proposed method better than existing method.

Keywords

Curve let method, Image fusion, Stero matching.

INTRODUCTION

Image fusion is a sub-field of image processing in which more than one images are fused to create an image where all the objects are in focus. Image fusion is of significant importance due to its application in medical science, forensic and defense departments. The process of image fusion is performed for multi-sensor and multi-focus images of the same scene. Multi-sensor images of the same scene are captured by different sensors whereas multi-focus images are captured by the same sensor. In multi-focus images, the objects in the scene which are closer to the camera are in focus and the farther objects get blurred. Contrary to it, when the farther objects are focused then closer objects get blurred in the image. To achieve an image where all the objects are in focus, the process of images fusion is performed either in spatial domain or in transformed domain. Spatial domain includes the techniques which directly incorporate the pixel Values[1]. In transformed domain, the images are first transformed into multiple levels of resolutions. An image often contains physically relevant features at many different scales or resolutions. Multi-scale or multi-resolution approaches provide a means to exploit this fact. After applying certain operations on the transformed images, the fused image is created by taking the inverse transform.

RELATED METHODS FOR IMAGE FUSION

Number of image fusion techniques has been presented. In addition of simple pixel level image fusion techniques, we find the complex techniques such as Laplacian Pyramid, fusion based on PCA, discrete wavelet (DWT) based image fusion, Neural Network based image fusion and advance DWT-based image fusion [2].

A number of image fusion techniques have been presented in the literature. In addition of simple pixel level image fusion techniques, we find the complex techniques such as Laplacian Pyramid, fusion based on PCA, discrete wavelet (DWT) based image fusion, Neural Network based image fusion and advance DWT-based image fusion.

ARTIFICIAL NEURAL NETWORK

The basic idea of IHS fusion method is to convert a color image from the RGB (Red, Green, and Blue) color space into the IHS (Intensity, Hue, Saturation) color space. One of the will be replaced by another image when we got the intensive information of both images [3]. Then we convert IHS color space with H and S of being replaced image into RGB color space. See the following procedure:

Step1: Transform the color space from RGB to IHS.

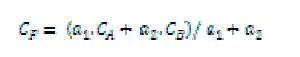Where Iv is intensity of visual image. R, G, B is color information of visual image respectively, 1 V and 2 V are components to calculate hue H and saturation S.

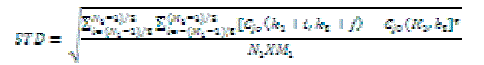Step 2: The intensity component is replaced by intensity of infrared image Ii.

Step 3: Transform the color space from IHS to RGB.

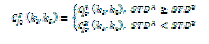Where Ii is intensity of infrared image.R', G’, B’ is color information of fused image respectively. Because our basic idea is to add useful information of far infrared image to visual image. We set fused parameters in the matrix instead of the intensity of far infrared image Ii to replace the intensity of visual image Iv [4]. The fused parameters will be adjusted according different information of each region. The following formula is modified result.

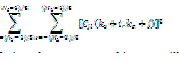Artificial neural network (ANN) has good advantage to estimate the relation between input and output when we could not know the relation of input and output, especially the relation is nonlinear. Generally speaking, ANN is divided into two parts. One is training, another is testing. During the training, we have to define training data and relational parameters [5]. In the testing, we have to define testing data then get fused parameters. It has good ability to learn from examples and extract the statistical properties of the examples during the training procedure. Feature extraction is the important pre-procedure for ANN. In our case, we choice four feature, respectively, average intensity of visual image Mv, average intensity of infrared image Mi , average intensity of region in infrared image Mir and visibility Vi to present as input of ANN. The following is our introduction of features.

The average intensity of visual image Mv:

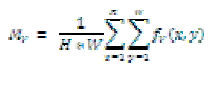Where is visual gray image, H and W are height and width of visual image. Generally speaking, it possible means the content of the image is shot in the daytime when Mvis larger [6]. On the other hand, the content of the image is shot in the night. But it is initial assumption, not accurate.

The average intensity of Mi is defined as follow:

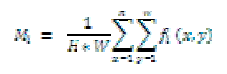Wherefi is infrared image, H and W are height and width of visual image. Generally speaking, it possible means the content of the image was shot in the daytime when Mi is larger. On the other hand, the content of the image was shot in the night. If we consider Mvand Mito assume the shot time, then we can do more assume that the image was shot in the daytime or night when Mvand Miboth are larger or smaller respectively [7]. If Mi is larger and Mvis smaller then we can suppose that the highlight of infrared image could be useful information for us. If Mi is smaller and Mvis larger than we can suppose that it could be no useful information in the infrared image to add to visual image. The average intensity of region in Mir is defined as follow:

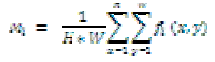Where DBiis the segmented region of infrared image. ΣDBiis the total number of pixels in the region DBi. We can suppose more accurately if we have above three features. For example, the biggest Mir could be not the information what we want if Miand Mvboth arelarger [8]. But we have to care about other regions which could be useful information in the same state.

THE ADVANCED DWT METHOD (FAST DISCRETE CURVE LET TRANSFORM)

The regular DWT method is a multi-scale analysis method. In a regular DWT fusion process, DWT coefficients from two input images’ are fused pixel-by-pixel by choosing the average of the approximation coefficients at the highest transform scale; and the larger absolute value of the detail coefficients at each transform scale. Then an inverse DWT is performed to obtain the fused image. At each DWT scale of a particular image, the DWT coefficients of a 2D image consist of four parts: approximation, horizontal detail, vertical detail and diagonal detail. In the advanced DWT (aDWT) method, we apply PCA to the two input images’ approximation coefficients at the highest transform scale, that is, we fuse them by using the principal eigenvector (corresponding to the larger Eigen value) derived from the two ‘original’ images.

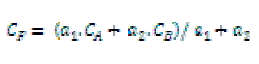where CA and CB are approximation coefficients transformed from input images A and B. CF represents the fused coefficients; a1 and a2 are the elements of the principal eigenvector, which are computed by analyzing the ‘original’ input images (Note: not analyzing CA and CB because their sizes at the highest transform scale are too small to conduct an accurate result). Note that the denominator in Eq. (13) is used for normalization so that the fused image has the same Energy distribution as the original input images. In combining the detail coefficients (the other three quarters of the coefficients) at each transform scale, the larger absolute values are selected, followed by a neighborhood (e.g., a 3×3 window) morphological processing, which serves to verify the selected pixels by using a “filling” and “cleaning” operation (i.e., the operation fills or removes isolated pixels locally) [9]. For example, in a 3×3 processing window (sliding pixel-by-pixel over the whole image), if the central coefficient was selected from Image A but all its 8- surrounding coefficients were selected from mage B, then after the ‘filling’ process the central one would be replaced with the detail coefficient from Image B. Such an operation (similar to smoothing) can increase the consistency of coefficient selection thereby reducing the distortion in the fused image.

The curve let transform has gone through two major revisions. The first generation curve let transform used a complex series of steps involving the ridge let analysis of radon transform of an image. The performance was exceeding slow. The second generation curve let transform discarded the use of the ridge let transform, thus reduced the amount of redundancy in the transform and increased the speed considerably. Two fast discrete curve let transform algorithm were introduced in [10]. The first algorithm is based on unequally-spaced FFT while the second is based on the wrapping of specially selected Fourier samples. In this paper, we focus on the “wrapping” version of the curve let transform.

Images can be fused in three levels, namely pixel level fusion, feature level fusion and decision level fusion. Pixel level fusion is adopted in this paper. We can take operation on pixel directly, and then fused image could be obtained. We can keep as more information as possible from source images. Because Wavelet Transform takes block base to approach the singularity of C2 , thus isotropic will be expressed; geometry of singularity is ignored. Curve let Transform takes wedge base to approach the singularity of C2 . It has angle directivity compared with Wavelet, and anisotropy will be expressed [11]. When the direction of approachable base matches the geometry of singularity characteristics, Curve let coefficients will be bigger.

First, we need pre-processing, and then cut the same scale from awaiting fused images according to selected region. Subsequently, we divide images into sub-images which are different scales by Wavelet Transform. Afterwards, local Curve let Transform of every sub-image should be taken; its sub-blocks are different from each others on account of scales’ change. The steps of using Curve let Transform to fuse two images are as follows:

a. Resample and registration of original images, we can correct original images and distortion so that both of them have similar probability distribution. Then Wavelet coefficient of similar component will stay in the same magnitude.

b. Using Wavelet Transform to decompose original images into proper levels. One low-frequency approximate component and three high-frequency detail components will be acquired in each level.

c. Curve let Transform of individual acquired low frequency approximate component and high frequency detail components from both of images, neighborhood interpolation method is used and the details of gray can’t be changed.

According to definite standard to fuse images, local area variance is chose to measure definition for low frequency component. First, divide low-frequency C jo(k1,k2) into individual foursquare sub-blocks which are N1 ×M1 ( 3×3 or 5× 5 ), then calculate local area variance of the current sub-block:

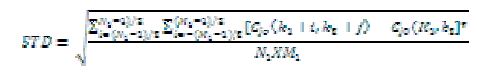If variance is bigger, it shows that the local contrast of original image is bigger, that means clearer definition. It is expressed as follows:

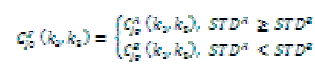Regional activity Ej,l (k1, k2) is defined as a fusion standard of high-frequency components. First, divide highfrequency sub-band into sub-blocks, then calculate regional activity of sub-blocks

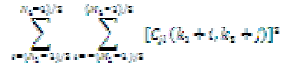Inverse transformation of coefficients after fusion, the reconstructed images will be fusion images.

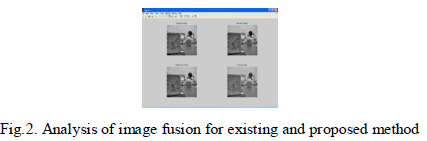RESULTS & CONCLUSION

The paper has presented a new trend in the fusion of digital image, MRI and CT images which is based on the curve let transform. A comparison study has been made between the traditional wavelet fusion algorithm and the proposed curve let fusion algorithm in the Fig.2. The experimental study shows that the application of the curve let transform in the fusion of MR and a CT image is superior to the application of the traditional wavelet transform. The obtained curve let fusion results have higher correlation coefficient and entropy values than in wavelet fusion results and minimum values of RMS error than in the wavelet transform.

References

1. H. Maitre and I. Bloch, “Image fusion”, Vistas in Astronomy, Vol. 41, No. 3, pp. 329-335, 1997.
2. S. Nikolov, P. Hill, D. Bull, and N. Canagarajah, “Wavelets for image fusion”, Wavelets in Signal and Image Analysis, Kluwer, Dordrecht, The Netherlands, pp. 213-244, 2001.
3. D. Ryan and R. Tinkler, “Night pilotage assessment of image fusion”,Proc. SPIE, Vol. 2465, Orlando, FL, pp. 50–67, 1995.
4. A. Toet and E. M. Franken "Perceptual evaluation of different image fusion schemes", Displays, Vol. 24, No. 1, pp. 25–37, 2003.
5. G. Piella, "A general framework for multi resolution image fusion: from pixels to regions", Information Fusion, Vol. 9, pp. 259–280, 2003.
6. H. Li, B. S. Manjunath, and S. K. Mitra, "Multisensor image fusion using the wavelet transform", Graphical Models and Image Processing, Vol. 57, No. 3, pp. 235–245, 1995.
7. O. Rockinger, “Image sequence fusion using a shift invariant wavelet transforms. Proc. IEEE International Conference on Image Processing, Washington, DC, pp. 288–291, 1997.
8. C. Xydeas and V. Petrovic "Objective pixel-level image fusion performance measure", In Proc. SPIE, Vol. 4051, Orlando, FL, pp. 88– 99, 2000
9. G. H. Qu, D. L. Zhang, and P. F. Yan “Information measure for performance of image fusion”, Electronics Letters, Vol. 38, No. 7, pp. 313–315, 2002.
10. Z. Wang and A. C. Bovik. “A universal image quality index” IEEE Signal Processing Letters, Vol. 9, No. 3, pp. 81–84, 2002.
11. G. Piella and H. Heijmans, "A new quality metric for image fusion" In Proc. Int. Conf. Image Processing, Barcelona, Spain, pp. 173-6, 2003.