ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Dipak D. Bage 1, K. P. Adhiya 2, Sanjay S. Gharde3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
There are several problems in pattern recognition system like feature extraction problem and identification, pre-processing and classification problem etc. One of the application domains in pattern classification is handwritten character or symbolic recognition. Identifying handwritten characters is always a complex and challenging task for the researchers. Wide research has been done on the character recognition but handwritten mathematical symbol recognition still remain either untouched or remarkably less research has been done. This is also treated as one of the subset of character recognition. Hence the new approach for offline handwritten mathematical symbol recognition system is described throughout this paper. Proposed system is identified by comparative study of feature extraction techniques. For this research, Character Geometry as feature extraction technique and support vector machine as a classifier is proposed. Proposed system can be useful in an embedded as well as mobile application. Also, it can be useful while converting pdf documents into word from where mathematical symbols can be correctly identified. So definitely it will be feasible in long run.
Keywords |
| Symbol recognition; support vector machine; feature extraction; Mathematical symbols. |
INTRODUCTION |
| Pattern searching in data is very historical issue and it is handled from hundreds of years. For example, most of the astronomical theories of Tycho Brahe in the 16th century discovered the empirical laws of planetary motion, which resulted into classical mechanics. The field of pattern recognition is concerned with the automatic discovery of regularities in data through the use of computer algorithms and with the use of these regularities to take actions such as classifying the data into different categories [1]. For Handwritten Mathematical Symbol recognition, the goal is to build a machine that takes a input vector x and identify of the Symbol 0- 9, a-z, A-Z, +, - etc. as the output. But problem lies in variations in handwriting. It can be handled using handcrafted rules or heuristics but it produces invariably poor results. The alternate and best solution for these better results can be obtained by adopting a Machine Learning approach [1]. In pattern recognition and in image processing, feature extraction is a particular form of dimensionality reduction. When the input data is too large to be processed and it is suspected to be notoriously redundant (much data, but not much information) then the input data will be transformed into a reduced representation set of features (also named features vector). Input data transforming into the set of features is called feature extraction [2]. Most scientific and engineering publications contain mathematical symbols and expressions. Recognition of handwritten mathematics would not only require less effort in writing technical documents but could also be used to transfer existing handwritten documents into electronic format and between machines when needed. Therefore handwritten mathematics recognition is one of the key forces that drive the information transformation between human and machine [3]. Handwritten mathematics recognition has been studied for over 30 years. As mathematical expressions appear in large number of scientific documents, without doubt transferring such documents into electronic format requires utilities for recognition of mathematical content. Handwriting input provides normal and suitable way of inputting mathematical text into computer for storage or sharing with others, once again underlining the necessity of effective mathematical recognition software. |
II. FEATURE EXTRACTION TECHNIQUES |
| Feature extraction techniques applied on online as well as offline input data set. So by considering both data sets following are some feature extraction techniques described in short. |
| A. Chain Code |
| Given a scaled binary image, first find the contour points of the character image. Here consider a 3 × 3 window surrounded by the object points of the image. If any 4-connected neighbour points are a background point then the object point (P), as shown in figure 2.1 is considered as contour point. The contour following procedure uses a contour representation called “chain coding” that is used for contour following proposed by Freeman, shown in figure 2.2 a. |
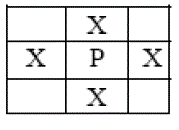 |
| Fig. 2.1 Contour Point Detection neighbour |
| Each following proposed by Freeman, shown in figure 2.2 a. Each pixel of the contour is assigned a different code that indicates the direction of the next pixel that belongs to the contour in some given direction. It provides the points in relative position to one after another, independent of the coordinate system. In this methodology connected neighbouring contour pixels, the points and the outline coding are considered. Following procedure may proceed in clockwise or in counter clockwise direction. Here, researchers have chosen to proceed in a clockwise direction [4]. |
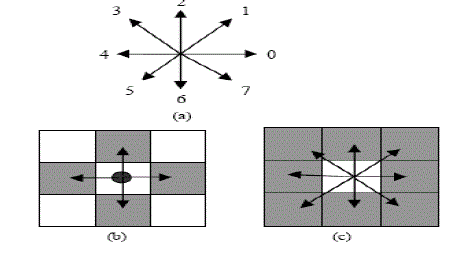 |
| Fig. 2.2: Chain Coding, (a) Direction of connectivity, (b) 4 - connectivity, (c) 8 – connectivity [4]. |
| B. Directional Features The first step required to simplify each character's boundary through identification of individual stroke or line segments in the image. Next, in order to provide a normalized input vector to the neural network classification schemes, the new character representation was broken down into a number of windows of equal size (zoning) whereby the number, length and types of lines available in each window was determined. 1) Determining Directions: The line segments that would be determined in each character image were categorized into four types: 1) Vertical lines, 2) Horizontal lines, 3) Right diagonal and 4) Left diagonal. Out of these four line representations, it also located intersection points between each type of line. To facilitate the extraction of direction features, the following steps were required to prepare the character pattern [5]. 1. Starting point and intersection point location 2. Distinguish individual line segments 3. Labelling line segment information 4. Line type normalization Following the steps described above, individual strokes in the character images are characterized by one of four numerical direction values (2, 3, 4 or 5). This process is illustrated in figure 2.3. 2) Formation of Feature Vectors: Once line segments were found, a methodology was developed for creating proper feature vectors. In first step, the character pattern marked with directional information was zoned into windows of equal size (the window sizes were varied during experimentation). In the next step, direction information was extracted from each individual window. Specific information such as the line segment direction, line segment length, its intersection points, etc. were state as floating point values between –1 and 1 [5]. |
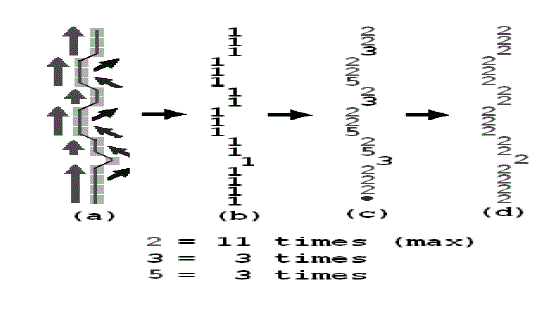 |
| Fig. 2.3: (a) Original line, (b) Line in binary file, (c) After distinguishing directions (d) After direction normalization [5]. |
| C. Local Features Local features- also known as Grid features can be extracted from gray level, binary and thinned images. From the small regions of whole image, local features are estimated, such as centre of gravity, width, height, horizontal and vertical projections, aspect ratio, area of black pixels of each grid region, normalized area of black pixels, gradient and concavity features etc. The global features can also be considered as local features for each grid region. To obtain a set of global and local features, both of these features sets are combined into a feature vector and the feature vector is sent as input to the classifiers for generating matching scores [6]. D. Global Features Global and local features contain information, which are effective for symbols recognition. Selection of different features is very important for any pattern recognition and classification technique. Global features are extracted from the whole symbol image. On the other hand, local geometric features are extracted from symbols grids. Moreover, each grid can be used to extract the same ranges of global features. Combination of these global and local features is further used to determine the symbol successfully from the database. This set of geometric features is used as input to the identification system [6]. E. Ink Related Features In the Ink Related Features following data we need to collect to identify symbols; Number of Strokes: This information is visible in the data structures returned by the ink collection. Point Density: We determine whether the ink density is most similar to the letter “o,” “p” or “b.” For o density, ink is evenly distributed in the whole stroke. With p density, ink is distributed in the upper part is more than that in the lower part, while for b density, ink is distributed in the lower part more than that in the upper part. To compute these, we divide the ink bounding box into three parts vertically, the upper 40%, the middle 20% and the lower box is 40%. We divide the ink bounding box into three boxes instead of two due to the variance in handwriting. For example, the lower part of letter “b” may occupy more than 50% of the symbol height [7]. F. Affine Moment Invariants Affine moment invariants (AMIs) are independent of actions of the general affine group and can be used in recognition of handwritten characters. A central moment of order p + q for a 2-dimensional object O can be represented as μpq = ∫∫O (x – xc)p (y – yc)q dxdy Where (xc, yc) is the centre of gravity of the object O. In the paper the first four affine moments were calculated to obtain a description of an isolated character in the form of a 4-dimensional vector. Samples were classified by the minimum distance to the training samples. The performance of AMIs is compared with that of the geometric moment invariants are invariant under the rotation, scale and translation. Affine moment invariants are important tools in object recognition problems. These techniques are commonly divided into two main categories according to how they make use of the image functions. So called as local approaches of the objects are segmented to smaller elements and invariants are computed separately for each of them. The second category consists of the global approaches; here features are computed directly from the whole image intensity function. The AMIs was derived by means of the theory of Algebraic invariants [8]. G. Character Geometry Universe of Discourse: At first, the universe of discourse is selected because the features extracted from the character image include the positions of different line segments in the character image. |
| Zoning: The image is divided into windows of equal size and feature extraction is applied to each individual zone rather than the whole image. In our work, the image was partitioned into 9 equal sized windows. Starters, Intersections and Minor Starters: To extract different line segments in a particular zone, the whole skeleton in that zone should be traversed. For this reason, particular pixels in the character skeleton are treated as starters, intersections and minor starters. Character traversal: Character traversal starts after zoning by which line segments in each zone are extracted. The first step is the starters and intersections in a zone are identified and then occupied in a list. Then the algorithm starts by considering the starter list. Once all the starters are processed, minor starters find along the course of traversal are processed. The positions of pixels in each of the line segments obtained during the process are stored. After visiting all the pixels in the image, the algorithm stops. Distinguishing the line segments: After all the line segments in the image are extracted, they are classified into any one of the following line-types – Horizontal line, Vertical line, Right-diagonal line, or Left-diagonal line. Feature Extraction: After the line type of each segment is determined, feature vector is formed based on this information which includes the number and the normalized length of the four different types of lines in each zone [9]. The normalized length of a line is given as; |
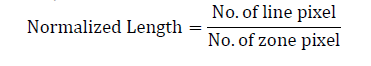 |
| After zone feature extraction, certain features are extracted for the entire image based on the regional properties, viz., Euler number, regional area, and eccentricity. By considering feature extraction techniques, we found symbols Geometry Feature Extraction as feature extractor because these produce 81 features respectively for each image. In this method we contain following steps which are shown in below in sub point 1. Universe of Discourse Universe of discourse is defined as the shortest matrix that fits the entire character skeleton. The Universe of discourse is selected because the features extracted from the character image include the positions of different line segments in the character image. So every character image should be independent of its Image size. |
 |
| Fig. 2.4: a) Original Image b) Universe of Discourse |
| 2. Zoning After the universe of discourse is selected, the image is divided into windows of equal size, and the feature is done on individual windows. For the system implemented, two types of zoning were used. The image was zoned into 9 equal sized windows. Feature extraction was applied to individual zones rather than the whole image. This gives more information about fine details of character skeleton. Also positions of different line segments in a character skeleton become a feature if zoning is used. This is because, a particular line segment of a character occurs in a particular zone in almost cases. For instance, the horizontal line segment in character ’A’ almost occurs in the central zone of the entire character zone [10]. 3. Starters, Intersections and Minor Starters To extract different line segments in a particular zone, the entire skeleton in that zone should be traversed. For this purpose, certain pixels in the character skeleton were defined as starters, intersections and minor starters. 5 Starters Starters are those pixels with one neighbour in the character skeleton. Before character traversal starts, all the starters in the particular zone is found and is populated in a list. |
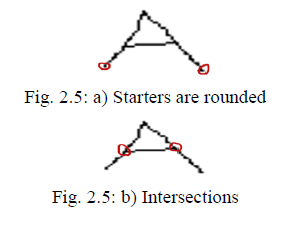 |
| B. Intersections The definition for intersections is somewhat more complicated. The necessary but insufficient criterion for a pixel to be an intersection is that it should have more than one neighbour. A new property called true neighbours is defined for each pixel. Based on the number of true neighbours for a particular pixel, it is classified as an intersection or not. For this, neighbouring pixels are classified into two categories, direct pixels and diagonal pixels. Direct pixels are all those pixels in the neighbourhood of the pixel under consideration in the horizontal and vertical directions. Diagonal pixels are the remaining pixels in the neighbourhood which are in a diagonal direction to the pixel under consideration. Now for finding number of true neighbours for the pixel under consideration, it has to be classified further based on the number of neighbours it have in the character skeleton. Pixels under consideration are classified as those with; • Three neighbouring pixels: If any one of the direct pixels is adjacent to anyone of the diagonal pixels, then the pixel under consideration cannot be an intersection, else if if none of the neighbouring pixels are adjacent to each other then it’s an intersection. • Four neighbouring pixels: If each and every direct pixel having an adjacent diagonal pixel or vice-versa, then the pixel under consideration cannot be considered as a intersection. • Five or more neighbouring pixels: If the pixels under consideration have five or more neighbours, then it is always considered as a intersection. Once all the intersections are identified in the image, then they are populated in a list. 5 Minor starters Minor starters are found along the course of traversal along the character skeleton. They are created when pixel under consideration have more than two neighbours. There are two conditions that can occur; |
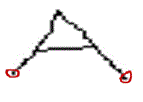 |
| Fig. 2.6: Minor starters |
| • Intersections: If current pixel is an intersection point. Then current line segment will end and all the remaining unvisited neighbours are populated in the minor starters list. • Non-intersections: Situations can occur where the pixel under consideration has more than two neighbours but still it’s not an intersection. In such cases, the current direction of traversal is found by using the position of the previous pixel. If any of the unvisited pixels in the neighbourhood is in this direction, then it is considered as the next pixel and all other pixels are occupied in the minor starters list. If not any of the pixels is not in the present direction of traversal, then the current segment is ended there and all the pixels in the neighbourhood are occupied in the minor starters list [10]. When the proposed algorithm is applied to character ’A’, in most cases, the minor starters found are given in the image. |
III. RESULT AND DISCUSSION |
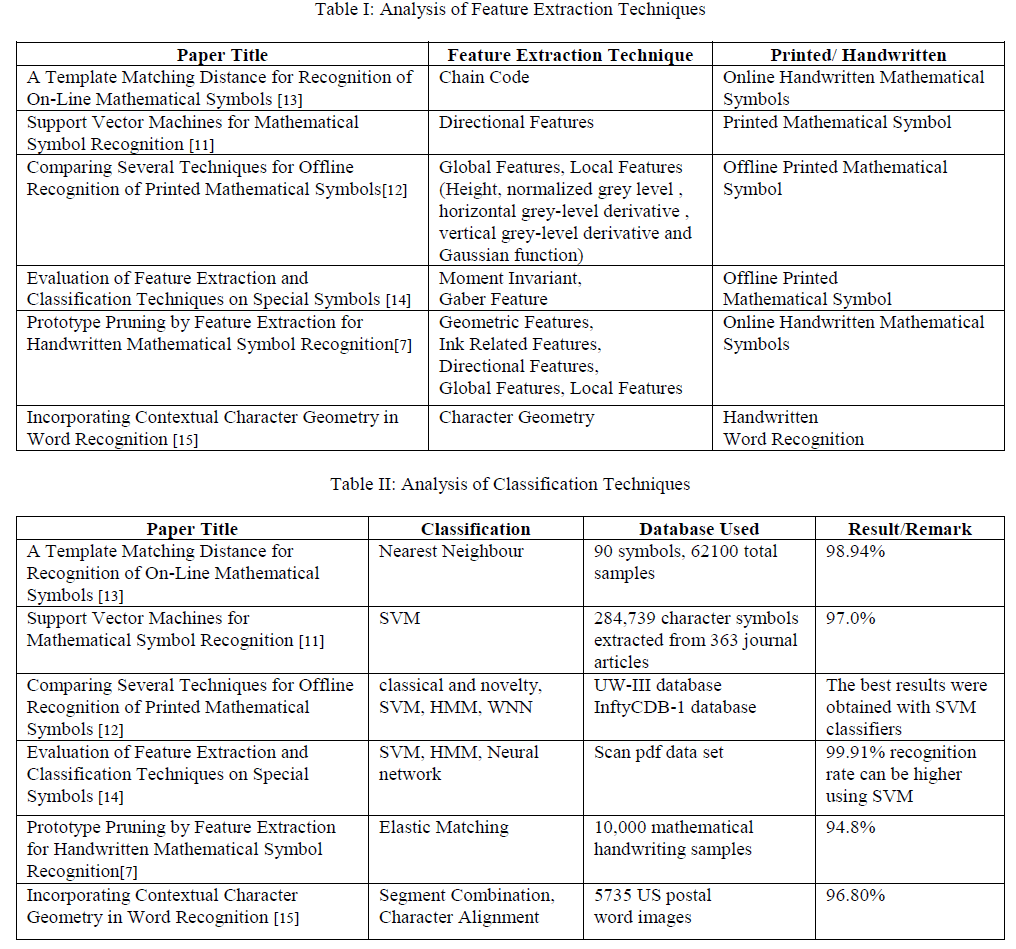
| In Image processing we can apply different feature extraction techniques for pattern recognition either individually or combining more than one. Pattern recognition can be available in two ways that is; in printed pattern and in handwritten pattern. Again printed or handwritten pattern performed using online and offline way. For recognition of pattern you can apply any feature extraction techniques with best supporting classifier so that you can achieve higher recognition rate. In this paper we will try to find out best feature extraction technique. And as per the analysis Character Geometry Feature Extraction Technique is one which support the different feature extraction techniques like; Local Feature Extraction Technique, Global Feature Extraction Technique, and Directional Feature Extraction Technique. Because as per the pattern required for these techniques are also used in Character Geometry. Summery about different Feature Extraction Techniques along with the classifier used in following papers; I. Support Vector Machines for Mathematical Symbol Recognition: In this paper Directional Feature Extraction Technique is used for printed mathematical symbols by using Support Vector Machine as classifier and achieved 97.0% recognition rate [11]. II. Comparing Several Techniques for Offline Recognition of Printed Mathematical Symbols: In this paper Local and Global Feature Extraction Techniques are used for offline printed mathematical symbols by using mixed classifier like Support Vector Machine, Hidden Markova Model, Weighted Nearest Neighbour etc. as classifier and conclude that best results were obtained with SVM classifiers [12]. |
| III. Prototype Pruning by Feature Extraction for Handwritten Mathematical Symbol Recognition: In this paper Geometric Features, Ink Related Features, Directional Features, Global Features, and Local Features were used for offline printed mathematical symbols by using Elastic Matching as a classifier [7]. By analysing these papers we seen that Character Geometry supports all features that are supported by Local, Global and Directional feature extraction techniques. Table I and Table II show analysis and study of different feature extraction and classification techniques respectively. |
 |
IV. PROBLEM DEFENITION |
| Offline or online handwritten character recognition is one of the application domains in pattern classification. Recognition of Handwritten Mathematical Symbols is a complicated task due to the unconstrained shape variations, different writing style and different kinds of noise. Also, handwriting depends much on the writer and because we do not always write the same digit in exactly the same way, building a general recognition system that would recognize any digit with good reliability in every application is not possible. Most researchers had applied SVM techniques on English, Persian, Chinese, Arabic, Tamil characters as well as symbols and acquired better recognition rate. We concentrated on the following areas: reducing the amount of computation, identifying discriminative features between symbols and building recognition models. Existing recognizers for, e.g., English, Chinese, Japanese and numbers have achieved reasonable processing rates based on small sets of symbols. In Asian languages there are many “characters”, but only small sets of strokes. When the lexicon increases, it is challenging to achieve high accuracy and speed. One goal should be to reduce the amount of computation for recognition when a large number of symbols are used. One way to do this would be to group handwritten mathematical symbols into classes, once proper criteria for such grouping have been found. Unknown symbols would first be placed into a group, followed by recognition within the group instead of comparing with the whole set of symbols. One goal of the present work is to identify those characteristics that may be used to separate characters into classes effectively. A common task in Machine Learning is to classify the data using training and testing. Support Vector Machine (SVM) is one of the better classifier among all Machine Learning algorithms for pattern recognition. So, linear SVM is chosen as classifier for getting the better recognition rate in our proposed work for classification. |
V. PROPOSED SOLUTION |
| With reference to literature work and problem statement, Handwritten Mathematical Symbols Recognition is the area of concern. All techniques implemented for this purpose are produced higher recognition rate. But these are leaving some scope for improvement. So, we concentrated on following work. a. Improving the accuracy of recognition, b. Selecting appropriate Feature Extraction Techniques, c. Extracting minimum features for classification. Proposed system follows all the necessary steps required to perform in Handwritten Symbol/Character Recognition System. Since internationally accepted standard dataset for Offline Mathematical Symbols is not available. Every researcher have implemented own dataset. We are prepared dataset for Mathematical Symbols by considering all possible constraints such as variations in writing styles, samples consisting with some noise, etc. |
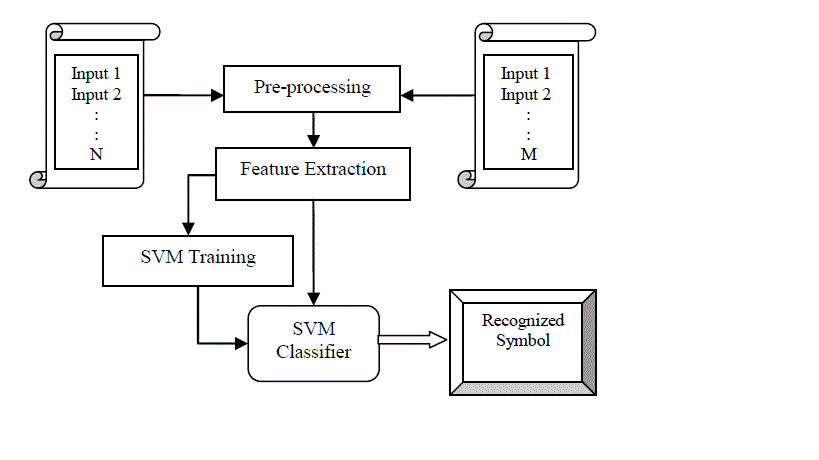 |
| Fig. 5.1: Architecture of Proposed System. |
VI. CONCLUSION |
| Different feature extraction techniques are explained along with Character Geometry. Basically these techniques are used for pattern recognition in different ways. Here we cover online as well as offline pattern recognition techniques for handwritten and printed character/symbols. For feature extraction techniques, we found that some techniques were follows unique features and some were follows mixed features for extracting features from image or input patterns. Character Geometry is a technique which supports different features they are supported by different techniques like Local, Global, and Directional features. These feature extraction techniques are used separately for symbols, characters and word recognition. Also it is found that Character Geometry is only used for character recognition purpose but yet not implemented for mathematical symbols. Linear SVM is under consideration as classifier for getting the better recognition rate in this work for classification. This is the proposed system and the implementation is going on. |