A New Ranking Scheme for Multi and Single Objective Problems

Abstract

Evolutionary algorithms (EAs) have received a lot of interest in last two decade due to the ease of handling the multiple objectives. But one of criticism of EAs is lack of efficient and robust generic method to handle the constraints. One way to handle the constraint is use the penalty method .in this paper we have proposed a method to find the objective when the decision maker (DM) has to achieve the certain goal. The method is variant of multi objective real coded Genetic algorithm inspired by penalty approach. It is evaluated on eleven different single and multi objective problems found in literature. The result show that the proposed method perform well in terms of efficiency, and it is robust for a majority of test problem

Keywords

Multi objective problem, Goal attainment method, Decision maker (DM),ID , dM, rank

INTRODUCTION

During the last few decades Evolutionary Algorithms (EAs) have proved to become an important tool to solve difficult search and optimization problems. Most real-world problems have constrained and EAs do not have a efficient and generic constraint handling techniques. The constrained optimization problem may be handled as a multi objective optimization problem as indicated by Coello Coello [2], Michalewicz [9] and Fonseca and Fleming [5]. Furthermore, EAs based on non-dominated sorting for multiobjective problems have received large interest during the past decades. Therefore it seems natural to look upon the constrained optimization problem as a multi objective problem. One of the interesting constraints handling method based on non-domination is presented by Deb et al. [7], Multi objective approaches of constrained problems based on Shaffers VEGA [11] is found in [12] [10].To directly apply a multi objective EA based on non-domination on a constrained optimization problem leads to a search of the best compromises of the objective value and constraint satisfaction, This whole set of solutions is usually not interesting since it is the optimal and feasible solution that is searched. Therefore it will not be efficient to directly apply a multi objective EA on a constrained problem; still the idea to handle the constrained problem with some variant of a multi objective EA is interesting.One of the most crucial steps in a multi objective EA is how to rank individuals. In this paper an alternative ranking scheme for the constrained single and multi objective problem is introduced. This ranking scheme is generic and no new parameters are introduced. The ideas of the ranking scheme are borrowed from the nondomination ranking for multiple objectives by Goldberg [6],Ander‟s ranking method [1] and Fonseca and Fleming ranking approach [4].The paper first defines the constrained optimization problem, and !hereafter the proposed method is presented in more detail.

II. PRELIMINARIES

a) Constraint optimization problem.

In this section the constraint optimization problem and its terminology is define. The constraint optimization problem or non -linear programming with „k‟ inequality constraint and „m‟ equality constraint is formulated as Minimize

III. THE PROPOSED APPROACH FOR CONSTRAINT OPTIMIZATION

In this section the proposed scheme is introduced .the new ranking scheme is used to formulate a scalar valued function that is used to rank individual in current population. Then selection, crossover, mutation and reinsertion are used in a standard manner for a real coded GA in this paper. Our main focus for this section is to define a new ranking scheme.

The approach is based on the following criteria.

 If no feasible individual exists in the current population , the search should be directed towards the feasible region.

 If majority of individuals in population are feasible , the search should be directed towards the individuals which satisfy the goal.

From the evaluation 5 onwards the number of feasible solution are increases hence the search will move to solution region which satisfy all the constraint and the more close to goal in order to study the behaviour during this situation we are taking the cases when the number feasible solution are 15% of total population and when the feasible solutions are 45% of population . circle shows the feasible solution and diamond shows the rest of individuals in population .square represent the most better individual (final_rank =0)

From the figure 2 the number of feasible solutions is less hence the weight of is less but still it moving towards the region where more number of feasible individuals can found which has values closer to the goal (by DM), and in figure 3 there are are almost double in number of feasible individuals compare to figure 2. As the number of evaluation increases the number of feasible individuals increases and more better solution will found. the number of feasible individuals are found during evaluation is represented in the Figure 3.

Figure 1 satisfy the criteria 1 i,e start wth random population and finding the feasible solution . figure 2 satisfy the criteria 2. i.e here have more than one feasible solution finding solution feasible solution closer to goal value(By DM).figure 3 satisfy the criteria 3 i,e the individual closer to goal is better than one which is away from goal.

V. CONSTRAINED MULTI AND SINGLE OBJECTIVE TEST PROBLEMS

It is always difficult to make fair comparisons between different EAs. Two different strategies may well have different optimal settings for the optimization algorithm parameters on the same problem. Another difficulty is to determine how to compare different algorithms. A naive but obvious way to compare algorithms is to compare the best solution found in the same number of function evaluations. A measure of the robustness of the algorithms is indicated by the spread of the best solutions found if the optimization is run several times independently. Here it is chosen to compare the results for the proposed ranking scheme with previously reported results for other EAs by other authors on a set of problems.

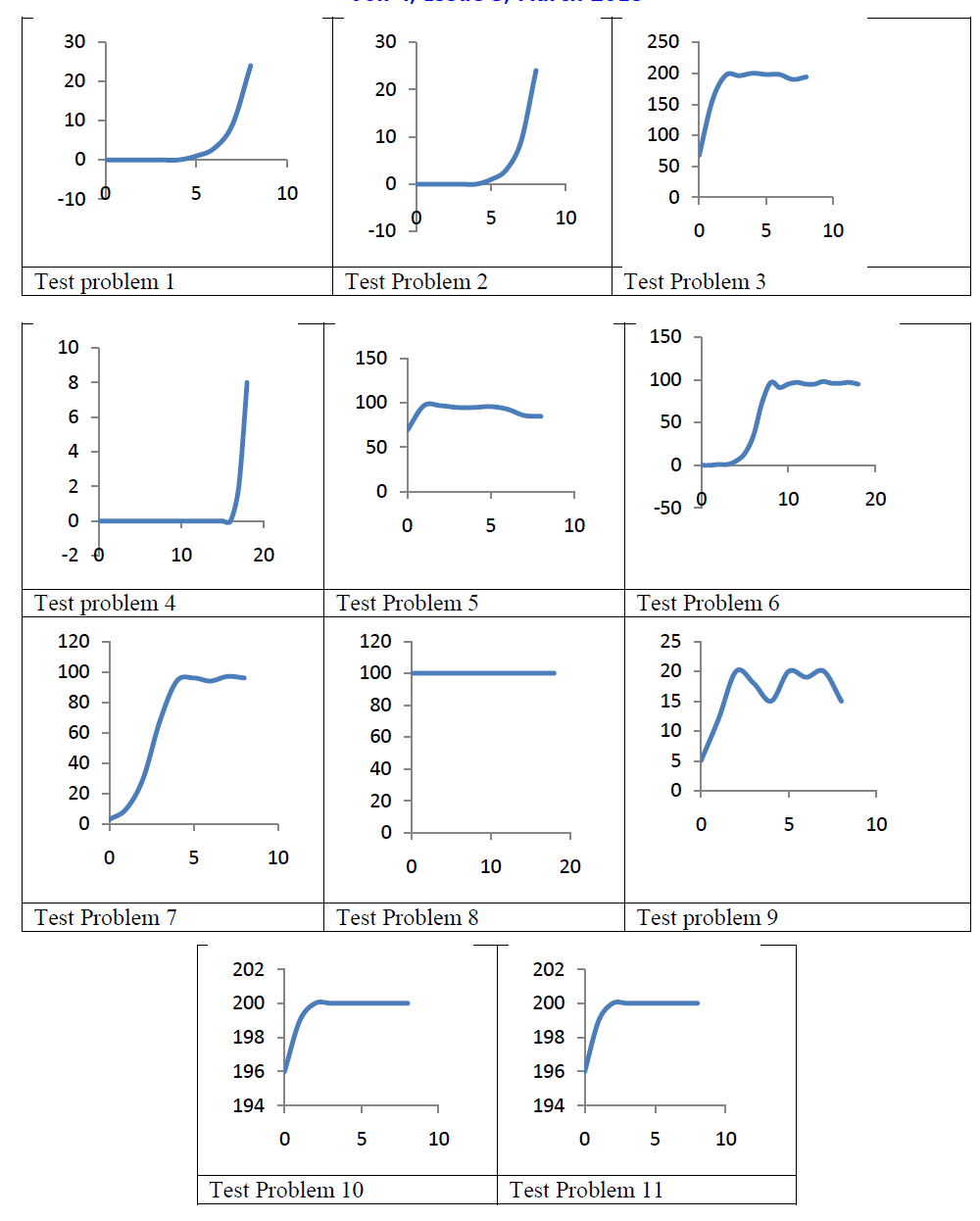
In this section we discuss the various test problems which are implemented by using the proposed method . graph shows the feasible solution at different iterations.

Our main purpose to solve the above problem by using propose ranking scheme therefore rest of parameters are taken as simple as possible here we have taken the NSGA II as our basic algorithm and the tournament selection method as selection method, PMXCrossover PolynomialMutation used as crossover and mutation respectively .This scheme will give more better answer if it used with more advance algorithm like adaptive genetic algorithm. The graphs shows the iteration Vs feasible solutions

VI. CONCLUSIONS

A general ranking scheme without problem specific extra parameters for constrained optimization problem has been presented. The performance for an algorithm with this ranking scheme has also been compared to the result of other ranking schemes with same algorithm on eleven problems, which are previously used by other authors. The results encourage further research since the method performs better than many other methods for the tested constrained single and multiple objective problems. It was only in the problem # 2 and #4 that this method did not perform well. It could not match up to the results for the other method for these problems (#2 and#4) either. The cause of this is an open question for further research. This method performed better in multi-objective (#5 to #11) problems as compare to other methods. It should also be mentioned that no effort has been made to study the optimal parameter settings such as population size, generation gap, mutation probability, etc.

VII. FUTURE WORKS

Our main purpose here is to proposed the new ranking scheme not to test the problems the result of this ranking scheme will more better if this scheme is tested with more advance algorithm like adaptive genetic algorithm and differential evolutionary algorithm . Here the goal value of the objective is arranged at start of ranking and throughout the ranking the goal values are constant. If the goal values also able to change as the generation increment then more better result can be obtain because the in real world the conditions changes very rapidly.

References

1. Anders Angantyr, Johan Andersson, Jan-Olov Aidanpaa.,Constrained Optimization based on a Multiobjective Evolutionary Algorithm
2. Coello Coello, C. A., 1999, “A Survey of Constraint Handling Techniques used with Evolutionary Algorithms”, Technical Report Lania- 1566 RI-99-04, Laboratorio Nacional de Informltica Avanzada, Xalapa
3. Floyd w gembicki and yacov y hames. “Approach to performance and sensitivity multiobjective optimization :goal attainment method “ .
4. Fonseca, C .M. and Fleming P.J.,1993,”Genetic Algorithms , Discussion and Generalization ”, in S .Forrest(Ed.),proceeding of international conference on Genetic Algorithm ,Morgan Kaufmann ,San Mateo ,CA, pp 416-423.
5. Fonseca, C. M. and Fleming, P. J, 1995, “Multiobjective Optimization and Multiple Constraint Handling with Evolutionary Algorithms 1: A Unified Formulation”, Research Report 564, University of Sheffield, Sheffield.
6. Goldberg,D.E ,- 1989,Genetic Algorithm in search,optimization and machineLearning , Addision-wesely , Reading.
7. kalyanmoy Deb, Amrit Pratap, Sameer Agrawal, T meyarivan .(KANGAL).,The Fast and Elitist multi objective Genetic algorithm: NSGAII
8. Michalewicz, Z., 1995, “A Survey of Constraint Handling Techniques in volutionary Computation Methods”, In J. R. McDonnell, R. G. Reynolds and D. B. Fogel (Eds.), Proceedings ofthe 4“ Annual Conference on Evolutionary Programming, MIT Press, Cambridge, MA, pp. 135-155,
9. M.M. Raghuwanshi and O.G. Kakde “Survey on multiobjective evolutionary and real coded genetic algorithms”.
10. Parmee; I; C. and Purchase; G., 1994,‟ “The development of a directed genetic search technique for heavily constrained search spaces!‟, In I. C. Parmee (Ed.), Proceedings of the Conference on Adaptive Computing in Engineering Design and Control, University of Plymouth, Plymouth, pp. 91- 102.
11. Schaffer, J. D., 1985, “Multiple objective optimization with vector evaluated genetic algorithms”, In J. J. Grefensttete (Ed.) Proceedings of the I” Int. Coilference on Genetic Algorithms, Hillsdale, New Jersey: Lawrence Erlbaum Associates, pp. 93-100.
12. Surry, P., Radcliffe, N., Boyd, I., 1995, “A multiobjective approach to constrained optimization of
13. gas supply networks”, In T. C. Fogarty (Ed.), Proceedings of the AISB-95 Workshop on Evolutionary Computing, Springer, Sheffield, pp. 166-1 80: