ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
S.Thiruppathi1, Mrs.S.Devi2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
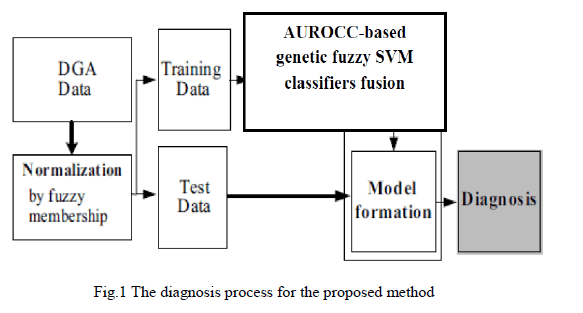
In this paper Ancillary service for Distributed Generation (DG) systems becomes a challenging issue to smartly integrate renewableenergy sources into the grid. Voltage control is one of these ancillary services which can ride through and support the voltage under grid faults. Grid codes from the transmission system operators describe the behaviour of the energy source, regulating voltage limits and reactive power injection to remain connected and supports the grid under fault. On the basis that different kinds of voltage sags require different voltage support strategies, a flexible control scheme for three phase grid-connected inverter is proposed here. For the three phase balanced voltage sags, the inverter should inject reactive power in order to raise the voltage in all phases. In one-phase or two-phase faults, the main concern of the DG inverter is to equalize voltages by reducing the negative symmetric sequence and clear the phase jump. Due to system limitations, a balance between these two extreme policies is mandatory. Thus, over voltage and under voltage can be avoided, and the proposed control scheme prevents disconnection while achieving the desired voltage support service. The main a contribution of this work is the introduction of a control algorithm for reference current generation that provides flexible voltage support under grid faults.
Keywords |
| Distributed Generation Inverters Reactive power control, voltage sag, voltage support |
INTRODUCTION |
| Total installed power from renewable-energy sources is constantly growing in the new electric deregulated scenario. Among them, photovoltaic and wind turbine are gaining increasing attention in the last few years [1], [2]. When connected to the grid, renewable energy sources behave as Distributed Generation (DG) systems. Smart energy networks [3]- 4] are receiving increased interest because of their potential advantages over conventional centralized systems, one of these advantages is that the energy production takes place closer to the consumer and real and reactive power losses can be minimized [5]. The inclusion of ancillary services allows for better resource utilization of the transmission system. Although, currently, new requirements are mainly focused on wind farms, in a near future, these requirements could be extended to small distributed suppliers [6]. |
| The basic element for interconnecting DG to the transmission system is the three-phase inverter. In normal grid conditions, three-phase DG inverters inject all the generated active power into the grid. One of the major drawbacks for proper operation of the whole system occurs when voltage sag is transmitted through the network. In grid fault conditions, the controller must react to the perturbation and mitigate the adverse effects on the inverter side. Depending on the depth and duration of the voltage sag, the grid codes force disconnection of the system. In this paper, a flexible control algorithm is proposed to face the problem of different types of voltage sags. Whenever balanced three-phase voltage sags occur, the voltage support strategy should raise the voltage in all phases as much as possible. However, if only one phase or two phases are in fault, a voltage equalizing strategy will be of interest. Then, it is possible to avoid under voltage in the phases under fault or over voltage in the phases that do not suffer the voltage sag. |
| Moreover, the negative-sequence voltage is reduced and the phase jump is cleared, which are important arguments to properly operate DG inverters [7]. To avoid disconnection, phase voltages must remain within upper and lower limits. Thus, a flexible strategy combining raising and equalizing capabilities, as proposed here, could be a better solution than conventional voltage support strategies to prevent from disconnection by under or over voltage. The analyze active and reactive power oscillations. Novel control schemes are needed for a greater penetration of DG sources. Better control algorithms improve power quality and efficiency and increase grid reliability as well [8].Therefore, control schemes with higher performance are the basis for proper operation of DG systems, particularly under grid faults. Many control algorithms designed to deal with grid disturbances are based on symmetric components [9]–[10]. |
II. PROBLEM FORMULATION |
| This paper focuses on current-mode threephase inverters to smartly support the grid voltage under fault. Inverter behaviour is commanded by the controller unit, which, according to [11] and [12] fulfil the following requirements: |
| 1) Active power control |
| 2) Reactive power control |
| 3) Voltage ride through |
| 4) Reactive current injection |
| 5) High power quality |
| In normal grid conditions, DG inverters must regulate both active and reactive powers injected into the grid. When the grid is in fault, voltage support control can mitigate voltage sag effects by injecting additional reactive current to ride through the perturbation and support the grid voltage. High quality of the injected currents is obtained when no harmonic distortion is present in the grid currents even during grid faults. |
A. Three-Phase DG Inverter |
| Fig. 1 shows the typical configuration of a three phase DG inverter. The complete system is composed of the power source (PS), the inverter, and the grid. Interconnection between the PS and the inverter is operated by a dc-link capacitor. The control of the dc-link voltage Vdc balances the power flow in the system. The inverter consists of a three-leg voltagesource pulse width-modulation inverter with an LCL filter to reduce high-frequency harmonics [13]. To avoid filter resonance, a passive damping resistor is included in series with the capacitor [14]. Finally, the DG inverter is connected to the grid at the point of common coupling (PCC). Grid impedance is mainly |
 |
| Inductive, so the inductance Lg is used to model the connection between the three-phase DG inverter and the grid. Grid voltage vg can be affected by the fault produced somewhere in the transmission system. |
B. Voltage Sag Characterization |
| Voltage sag is an abnormal condition in the grid voltages, characterized by a short-time reduction in one or various phases. The causes of voltage sags are mainly phase to ground short circuit, phase-tophase (to ground) short circuit, and the start-up of large motors. The most widely accepted classification of voltage sags is presented in [15]. Voltage sags can be characterized by the module, frequency and initial angle of each phase or by the positive, negative, and zero symmetric sequences |
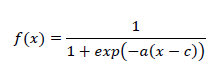 |
| Where the super indexes (+, −, and 0) indicate the positive, negative, and zero symmetric sequences, respectively. In three wire systems, zero sequence voltage v0 and current i0 are not present. Instead of using a natural frame for characterizing the grid voltage, the Clarke transformation is applied to express measured voltages in the stationary reference frame (SRF) |
C. Grid Code Requirements |
| TSO requirements in grid codes state that power generators should remain connected even in faulted grid conditions in order to feed the grid and support the grid voltage. Different TSOs provide different voltage profiles as limits for disconnection [16], [17], depending on sag depth and duration. |
| During a short interval (typically, less than 0.150 s), the inverter must remain connected even in very deep sag conditions [0.2 per unit (p.u.)]. In moderate voltage sags (below 0.8 p.u.), the inverter must remain connected for a longer time (2 s). Another issue in voltage support requirements is the reactive/ active power ratio. In deep voltage sags, only the reactive power must be injected to the grid. However, in less deep voltage sags, both active and reactive powers must be transferred to keep feeding the grid. |
D. Control of Three-Phase DG Inverter under Fault |
| The behaviour of the current-mode threephase inverter is determined by the injected current at the PCC. By injecting reactive power into the grid, the rms voltage at the PCC can be increased to support the grid voltage under fault. Then, a proper reference current generator is required when the grid is under fault in order to counteract the voltage sag effects on the system. In Fig. 2, a block diagram of the controller for DG inverters under grid fault is shown. The inputs of the controller are the measured phase voltages v at the PCC, the currents i flowing through Li inductor, and the dc-link voltage Vdc. Voltage v and current i am transformed into SRF values. Voltages vα and Vβ are then decomposed into symmetric components using a sequence extractor. The symmetric sequence extractor is a key aspect to characterize the grid voltage. Many sequence extractors can be found in the literature to extract voltage sag information at run time. The dc-link voltage regulator is in Charge of the active power reference P∗ that keeps power balance. |
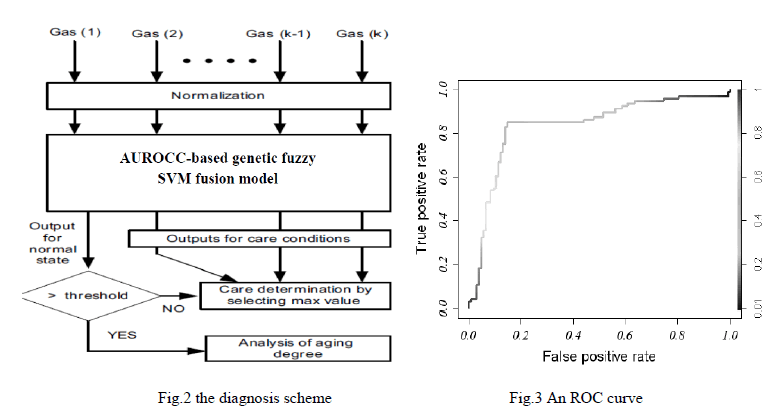 |
| The voltage support block needs first to detect the voltage sag. This can be done by computing the voltage rms in each phase. When one or several rms values drop below a predefined threshold, the voltage support control is activated. The voltage support block decides which strategy should be implemented according to grid codes and system limitations. |
| This part provides the reactive power reference Q∗; for the sake of simplicity, in this study, this reference is computed offline, and no closed loop is implemented. All this information passes through the reference generator to build reference currents i∗ α and i∗ β. The reference current generator is the kernel of the control algorithm because it can flexibly support the grid voltage. At the end of the current control loop, duty cycles dα and dβ are processed by the space vector pulse width modulator to commute the switches u1, u2, . . . , u6. |
III.FROM CONVENTIONAL TO PROPOSED CONTROL |
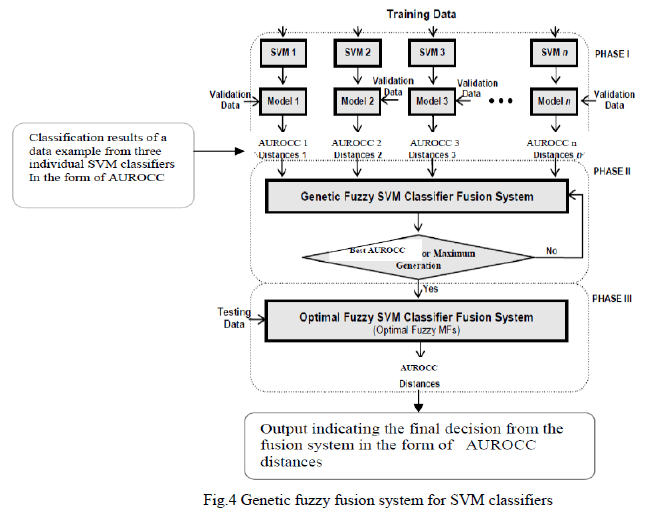
1. Controller Design |
| Under grid connected operation DG should be should be synchronized with the grid. In this mode each DG inverter works for the system by the measured voltage and desired power levels. For unity power factor operation, it is essential that the grid current reference signal is in phases with the grid voltage. Current controller design using Flexible Voltage Support Controller is shown in fig.3 |
 |
2. Point of Common Coupling |
| The PCC is a point in the electrical system where multiple customers or multiple electrical loads may be connected. According to IEEE-519, this should be a point which is accessible to both the utility and the customer for direct measurement. Although in many cases the PCC is considered at the metering point, service entrance or facility transformer, IEEE-519 states that “within an industrial plant, the PCC is the point between the non-linear load and other loads.” PCC at service entrance, metering point or facility transformer it will generally be easier to meet harmonic distortion limits when the PCC is considered at the metering point, facility transformer or service entrance. |
| In most cases, the current flowing at this point represents a combination of pure fundamental current flowing to linear loads and both fundamental and distorted current flowing to non-linear loads. The distortion current will often be a smaller percentage of the total (combined) fundamental current at this point. PCC within the plant and between the non-linear and linear loads Considering the PCC at the equipment will often meet the IEEE-limits both at this point and also at a PCC near the service entrance. The IEEE-519 limit at this point, which is essentially at the input to the non-linear loads, is often 12%, 15% or even 20% THD-I. |
| The ratio of short circuit current to load current is typically much larger at this PCC, which typically has less total load, than at the metering point, where the entire plant load is connected. Usually, if the THD limit is met at each non-linear load within the plant, the TDD limits at the service entrance will also be met. Even though the THD limits are typically lower for the PCC considered near the utility metering point, the overall THD at this PCC may be considerably lower if there are additional linear loads in the plant that share the power source. |
3. Filter |
| The rectifier circuitry takes the initial ac sine wave from the transformer or other source and converts it to pulsating dc. A full-wave rectifier will produce the waveform shown to the right, while a halfwave rectifier will pass only every other half-cycle to its output. This may be good enough for a basic battery charger, although some types of rechargeable batteries still won't like it. In any case, it is nowhere near good enough for most electronic circuitry. |
| We need a way to smooth out the pulsations and provide a much "cleaner" dc power source for the load circuit. To accomplish this, we need to use a circuit called a filter. In general terms, a filter is any circuit that will remove some parts of a signal or power source, while allowing other parts to continue on without significant hindrance. In a power supply, the filter must remove or drastically reduce the ac variations while still making the desired dc available to the load circuitry. |
| Filter circuits aren't generally very complex, but there are several variations. Any given filter may involve capacitors, inductors, and/or resistors in some combination. Each such combination has both advantages and disadvantages, and its own range of practical application. If we place a capacitor at the output of the full-wave rectifier as shown to the left, the capacitor will charge to the peak voltage each halfcycle, and then will discharge more slowly through the load while the rectified voltage drops back to zero before beginning the next half-cycle. |
| Thus, the capacitor helps to fill in the gaps between the peaks, as shown in red in the first figure to the right. Although we have used straight lines for simplicity, the decay is actually the normal exponential decay of any capacitor discharging through a load resistor. |
| The extent to which the capacitor voltage drops depends on the capacitance of the capacitor and the amount of current drawn by the load; these two factors effectively form the RC time constant for voltage decay. As a result, the actual voltage output from this combination never drops to zero, but rather takes the shape shown in the second figure to the right. The blue portion of the waveform corresponds to the portion of the input cycle where the rectifier provides current to the load, while the red portion shows when the capacitor provides current to the load. |
| As you can see, the output voltage, while not pure dc, has much less variation (or ripple, as it is called) than the unfiltered output of the rectifier. A half-wave rectifier with a capacitor filter will only recharge the capacitor on every other peak shown here, so the capacitor will discharge considerably more between input pulses. Nevertheless, if the output voltage from the filter can be kept high enough at all times, the capacitor filter is sufficient for many kinds of loads, when followed by a suitable regulator circuit. |
IV.RESULTS AND DISCUSSION |
1. Over All Simulation Diagram with Symmetrical Fault |
| The modelling of the system with flexible voltage support control is designed in simulink. The gain parameters of flexible voltage support controller obtained by proper tuning. Flexible voltage support control works as a regulator of the voltage and current during transition from grid connected to Symmetrical Fault. α and β for flexible voltage support control is chosen proper tuning. The Overall Simulation Diagram with Flexible Voltage Support controller Fig 3. |
 |
2. over all Simulation Diagram with Unsymmetrical Fault |
| The modelling of the system with flexible voltage support control is designed in simulink. The gain parameters of flexible voltage support controller obtained by proper tuning. Flexible voltage support control works as a regulator of the voltage and current during transition from grid connected to Unsymmetrical Fault. α and β for flexible voltage support control is chosen proper tuning. The overall Simulation Diagram with Flexible Voltage Support controller fig4. |
 |
3. Grid Voltage and current for symmetrical fault |
| The grid voltage and current waveforms without fault is shown Fig.6. The grid voltage is 565V and current value is 25A. |
 |
| The grid voltage and current waveforms without fault is shown Fig. 6. The grid voltage is 560V and current value is 40A.The Fig.6 shows the voltage and current value of grid and interconnection of solar power plant and three phase conventional source. In the Fig 6, Unsymmetrical condition the voltage and current values are calculated by using voltage current measurement. Here R&Y phases are fault condition. The grid voltage value in RY&B phases -565V per phase and grid current value in B phase 40A in R&Y phases 38A. So reduces the fault current values with in limit using reactive power injection in normal condition. |
V. CONCLUSION |
| A flexible voltage support control scheme has been proposed in this paper for three-phase DG inverters under a grid fault. The voltage support strategy can be modified by means of a control parameter according to the type of voltage sag. In three phase balanced sags, the best solution seems to be to raise the voltage in all phases. In one or two-phase faults, voltage equalization is a preferred choice because conventional strategies can lead to overvoltage and cause disconnection. When the sag is less deep, a balance between these two extreme policies should be implemented. |
References |
|