A Power Quality Compensator With Renewable
Energy Source Interface Capability Using Active
Power Filter

R.Mahendran; Mr. J. Praveen Daniel; Dr. C. Nagarajan

A Power Quality Compensator With Renewable Energy Source Interface Capability Using Active Power Filter

R.Mahendran¹, Mr. J. Praveen Daniel², Dr. C. Nagarajan³

P.G Scholar, Dept of Power Systems Engg, M.Kumarasamy College of Engg, Karur, Tamilnadu, India
Asst. Professor, Dept of EEE, M.Kumaransamy College of Engg, Karur, Tamilnadu, India
Prof & Head,Dept of EEE, Mythayammal Engg College,Namakkal, Tamilnadu, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Renewable energy sources are a reliable alternative to the conventional energy sources. This paper presented an capable of expandable grid-connected distribution generation interconnection of 3 phase 3 wire system for reactive power compensation. The proposed system not only, can control the active power flow but also mitigate the load unbalance and harmonics, and manage reactive power. All of these functions may be accomplished either individually or simultaneously. So the performing an active power balance by controlling the RES voltage level for the whole system. With the proposed approach, to shape the grid currents into sinusoidal currents in phase with the grid voltage waveforms and with an amplitude depending on the power available from renewable sources. On the other hand the load harmonics current will reduced by injecting into the alternating current system harmonic currents with an opposite phase.

Keywords

Renewable Energy Sources (RES), Active Power Filter (APF), Power Quality (PQ), Grid Interconnection.

INTRODUCTION

The load will be changed in nonlinearly then the reactive power compensation will be increased so the power system losses are increased. Due to this nonlinear loads the current harmonics are increases in the transmission lines, rotating machines, and transformers. Furthermore, harmonics and unbalance load causes the oscillatory torque in the sensitive equipment it's leading to malfunctions of the equipment’s, and also interference with communication circuits. So to overcome these harmonics current by using the Active Power Filter(APF) which have been successfully developed [1],[2].

Resent days the fossil fuel is the major role in the energy generation, but its lead to a major environmental problems so to avoid these problems the mankind to look for alternative resources in power generation[3]. Interest in renewable energy is increasing due to concerns about global warming, air quality, and sustainability.Renewable energy source (RES) integrated at the distribution level is termed as distributed generation (DG) the current controlled voltage source inverters are used to interface the intermittent RES in distributed system[4]. To perform the active power flow control there is no need of External hardware devices of the proposed method. The Renewable generating units with the active filter capability may play an important role in power quality management in future power systems.

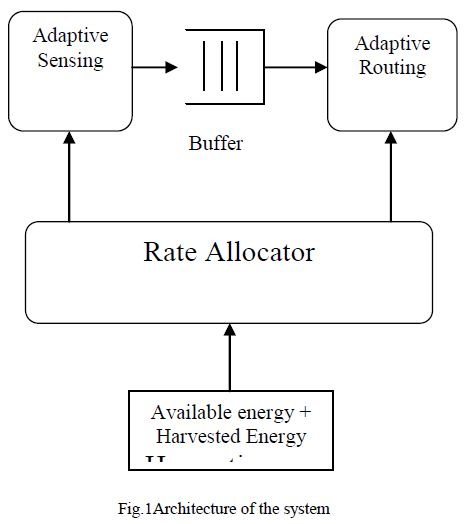From these block diagram shown in fig. 1, the DG source are like as a solar(pv), wind and fuel cell, etc. and the converter is a bipolar voltage source inverter and the nonlinear load.

To interconnect the Distribution Generation(DG) units with the Active Power Filter(APF) capability and two separate controllers have been designed for the DG interface[5] wherein the Solar(PV) system can act as a solar power generator on sunny days and an APF on rainy days. An APF applications the reference current is generated by using less computation time and some stored coefficients if compared with those required by the DFT[6]. Conventional DGs are based on renewable energy sources require a power electronic converter to interfacing with the utility grid because the generated power is DC or has an AC frequency that is either non constant or higher than the grid frequency[7]. Based on local measurement and agent-based communication, the power electronic converters were designed to provide non-active power in addition to active power supply in order to compensate distorted current[8]. Using adaptive neural filtering for harmonic analysis, a single-phase DG system with active power filtering capability was devised for utility current harmonic compensation [9].

A Z-source inverter-based flexible DG system was designed to improve grid power quality [10]. By successfully integrating power electronics converters and new generation technologies, the distributed generation has become more and more competitive against the conventional centralized system and attracted many customers from industrial, commercial, and residential sectors[11]. The integration of a positive and negative sequence SRF-PI controller of inverter output voltage has been proposed in[12]. Based on adaptive linear neuron control, the DG interface is utilized to control the active power flow, and to manage the reactive power of the power system[13]. The negative-sequence current compensation with a shunt converter has been presented in[14] and[15], and that with a series converter has been introduced in[16]. The repetitive control system has been proven to be a very effective and practical method dealing with periodic signals. Repetitive control has some similarities with iterative learning control[17].

GRID CONNECTED DG SYSTEM

In this paper, the Distributed Generation(DG) is interconnected to the Three-Phase grid with the help of the Active Power Filter. The simple Three-Phase Grid connected DG interface is shown in fig. 2, where Isn(t) (n =a, b, c) and Vs are the grid current, and voltage respectively, and Iun(t) (n = a, b, c) is the converter output current, and Iln(t) (n=a, b, c) is the load current.

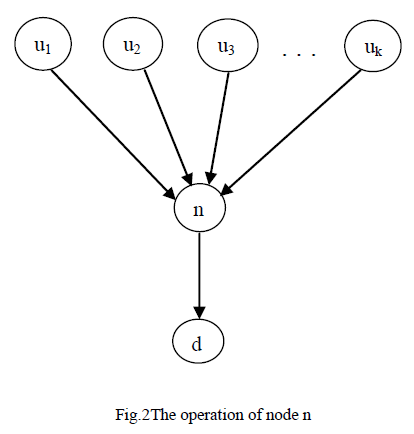A. Non-Linear Load

The nature of non-linear loads has to produce harmonics in the current waveform so the current waveform will be distorted and this distortion leads to distortion of the voltage waveform. For these conditions, the voltage waveform is no longer depends to the current. This load current contains all ODD harmonics. It is Can’t be categorized as leading or lagging Loads. If the load is considered as a non-linear load its impedance changes with the supply voltage. At the time of impedance changing that the current drawn by the nonlinear load will not be sinusoidal even when it is connected to a sinusoidal voltage. This non-sinusoidal current contains the harmonic currents that will interact with an impedance of the power distribution system to create the voltage distortion that can affect both the loads connected to it and the distribution system equipment. Essentially very high inrush current (20 time of I Normal) at the time of starting. For examples of the nonlinear loads are like as a Computers, laser printers, SMPS, TV, Rectifiers, Refrigerator, etc.

B. Distribution Generation(DG)

Now a days the available level of the natural resources (coal, natural gases and oil, etc.) are reduced and also it is the major causes of the environmental pollutions. So we need to move an alternative sources of renewable sources for the power generation. Normally the renewable sources are solar, wind, hydro, fuel cells, etc. For this paper the solar (PV) and wind energy is used as a DG. In this paper, a unified control method is proposed for a simple three-phase DG interface with a series diode for preventing power reversal to transmit active power, mitigate load unbalance and harmonics, and compensate reactive power. So the DG can perform the two functions of power station and APF as simultaneously or either one.

From fig. 2, the diode is used to avoid the power reversal from the grid during the rainy days and When the DG source injects active power to the dc capacitor C, it will accumulate the dc voltage level, while the DG interface will maintain the voltage level by transmitting the active power to the grid. On the contrary, when there is no DG source, the DG interface will maintain the voltage level by absorbing power from the grid for acting as an APF.

SHUNT ACTIVE POWER FILTER

In recent years, the power electronic converters are widely used in industrial and as well as domestic applications for the control of power flow. These converters take the advantages of all the recent advances and improvements of power electronics; affect from the problem of drawing non-sinusoidal current and reactive power from the supply. Their contributions to the waveform distortion is of growing interest, and are responsible for different power quality problems, led to implementation of standards and guidelines such as IEEE-519. Active power filters(APFs) are researched and developed as a viable alternative over the conventional methods to solve these problems [1], [2]. The APF can compensate harmonics and reactive power requirement of the nonlinear load effectively. Presently, APFs are designed to absorb all of the harmonics generated and/or reactive power required by the load and make the source current sinusoidal. The size and cost of APF depends on harmonics and reactive power to be compensated. For this paper proposed a new control algorithm for shunt APF to compensate the harmonics and reactive power requirement of nonlinear loads, and maintain similar distortion in the compensated current as present in the voltage. Therefore, the load behaves as a linear load, and the resultant source current will have the same waveform as that of the supply voltage. So that reactive power is completely compensated, and unity power factor (UPF) operation can be achieved. UPF operation also provides more effective reduction of voltage total harmonic distortion (THD) at network bus and lower harmonic losses. The proposed scheme provides an additional feature of compensation of either harmonics reduction, or the compensation of both harmonics and reactive power simultaneously. It’s based on the desired capacity of the APF. It maintains similar distortion level as present in the voltage, thereby attributing the responsibility of the customer and utility at the point of common coupling (PCC).

A. Mathematical Expressions

The any non-sinusoidal signal can be expressed as a sum of sinusoidal signals of various frequencies. Based on this the utility voltage and current can be expressed as

where, vs(t) and iL(t) are the instantaneous spply voltage and load current, Vn and In are the maximum value of nth-order voltage and current, ÃâÃÂ²n and Φ are the phase angle of nth-order voltage and current, and n is the order of harmonics.

The reference current drawn from the source is the portion of the current, which retains the same level of distortion as of the voltage, at the same time accounts for the entire fundamental frequency component. The reference current should have the same graphical pattern of variation as the voltage. It might have a time leg or lead, or may be in phase with the voltage, depending on either only harmonics or both reactive power and harmonics compensation capability. Thus, the fundamental frequency component of the load current (plus loss component, ILOSS) will be equal to the fundamental frequency component of the reference current for harmonic compensation, and I1cosΦ1(plus ILOSS) for both harmonic and reactive power compensation. which can be mathematically expressed as follows

For harmonic compensation

where is*(t) is the instantaneous value of the calculated reference current. The difference of reference and load current will flow from the APF and should be attributable to the customer.

HARMONIC CURRENT COMPENSATION BY SHUNT ACTIVE POWER FILTER

The fundamentals of APFs have already been explained in [1], [2], whereas only the major effect on current harmonic compensation with shunt active filters is shown here. A shunt APF can be seen as a controlled current source that injects a compensating current I on the basis of the load current IL, which is the input of a transfer function H. The harmonic current source (load) can be studied by its equivalent Norton circuit, which consists of an ideal current generator ILG with an in parallel impedance ZHL, globally absorbing the load current IL.

With the reference to Fig. 4, the following steady-satate current equations at the coupling point can be written as follows:

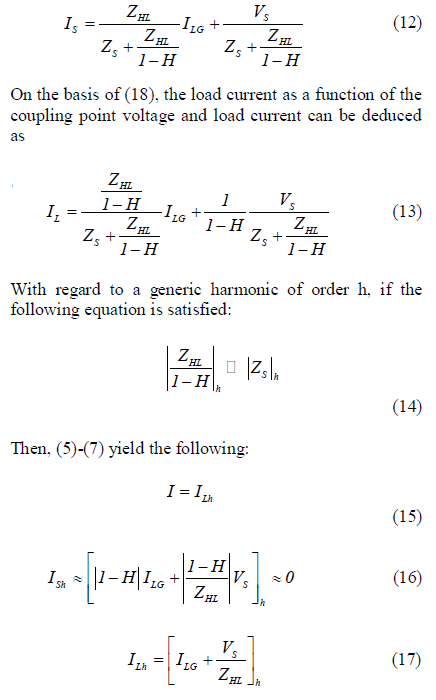Equation (15) shows that the grid supplies a current IS which is almost sinusoidal if (13) is satisfied for each harmonic of order h. Therefore, (13) is the operating condition of the shunt active filter to cancel the load harmonic current. Looking at (13), it should be observed that only H is a design parameter of the filter, whereas ZHL and ZS are the system parameters. The capability of the APF to cancel the load current harmonics depends thus not only on the filter itself (H) but also by the load (ZHL) and source (ZS) parameters. However, if

The harmonic compensation capability is independent from the system impedances. On the contrary, if

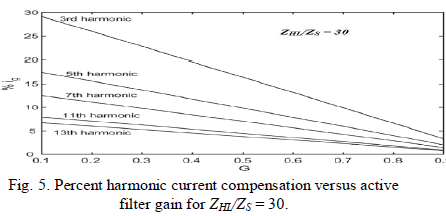
This means that, for a pseudo ideal current load, the compensation characteristics of the APF does not depend on the source impedance ZS even if |1 − H|h ≠ 0, which is the real advantage of the active filter over the passive one. In the ideal case, transfer function H should equal zero for the fundamental harmonic and one for all other harmonics. In practice, values of 0.7 ≤ |H| ≤ 0.9 are acceptable for higher harmonics. Fig. 5 shows a set of curves representing the low frequency harmonic amplitudes of the line current, in percent of the fundamental of the load current (assumed to be a square waveform), versus the active filter gain for a fixed value of the ratio |ZHL|/|ZS| = 30. It shows that with H = 0, the harmonic content of the line current is obviously the greatest, and no current harmonic compensation occurs. According to (17), the higher the gain H, the lower the harmonic of the line current. When G approaches one, all the harmonics of the line current become close to zero, independently from the harmonic order and the ratio |ZHL|/|ZS|.

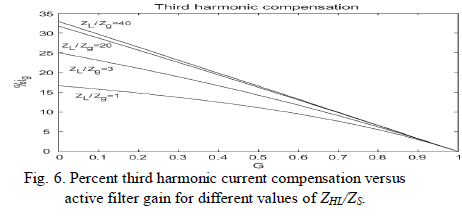Fig. 6, shows that, for lower values of H there is a dependency of the third harmonic on the grid impedance. The higher the ratio |ZHL|/|ZS|, the lower this dependency as explained above. For values of G close to one, the third harmonic amplitude is almost independent from the impedance ratio.

SIMULATION RESULT

The proposed APF was studied using simulation tools and advanced continuous simulation language (ACSL). Table I shows system parameters and load conditions under the unbalance.

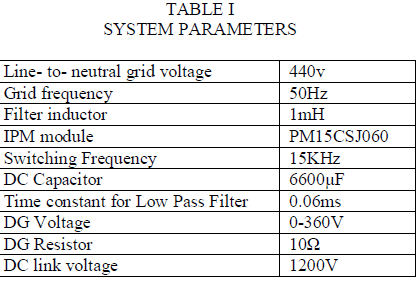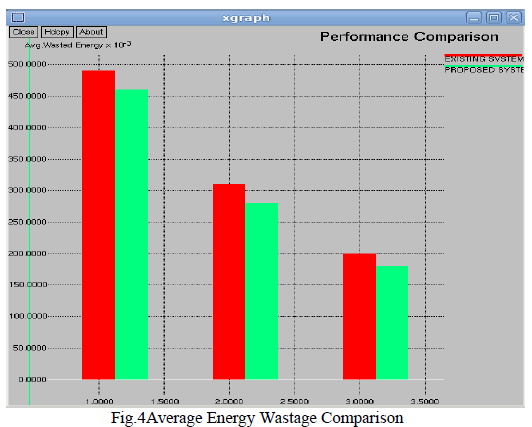
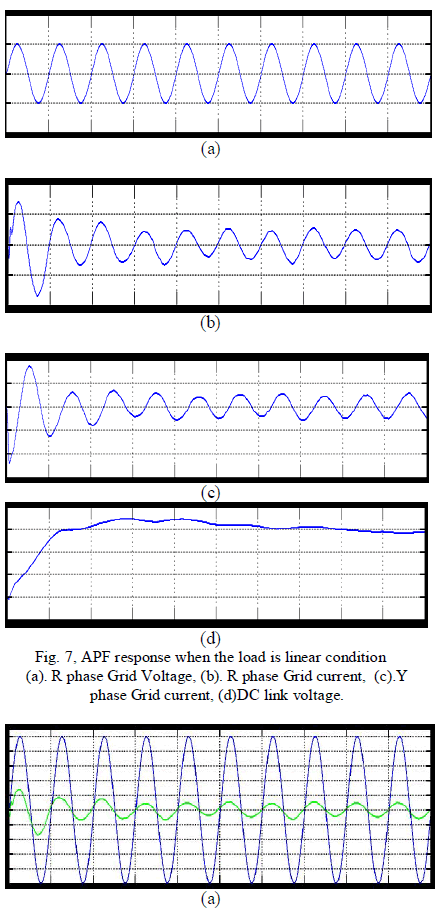
First consider the linear load condition at the time the following experimental result will be obtained, it’s shown in the fig. 7, and 8, from these graph when the load will be changed as linearly then the source side power flow will be linearly that is source side voltage and current is sinusoidal at the time the reactive power compensation is not required. And the capacitor will be charged for their maximum value. In here the capacitor value is set as 6600 micro farad. From these simulation result we can analyse the system performance of the overall power system network.

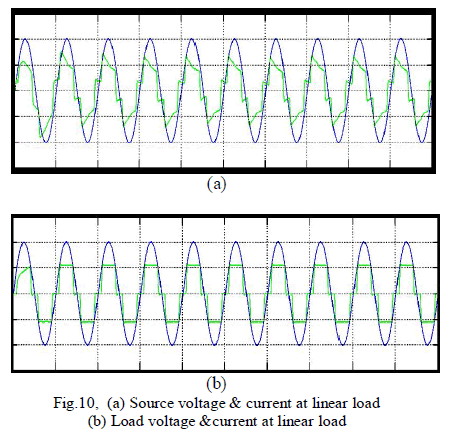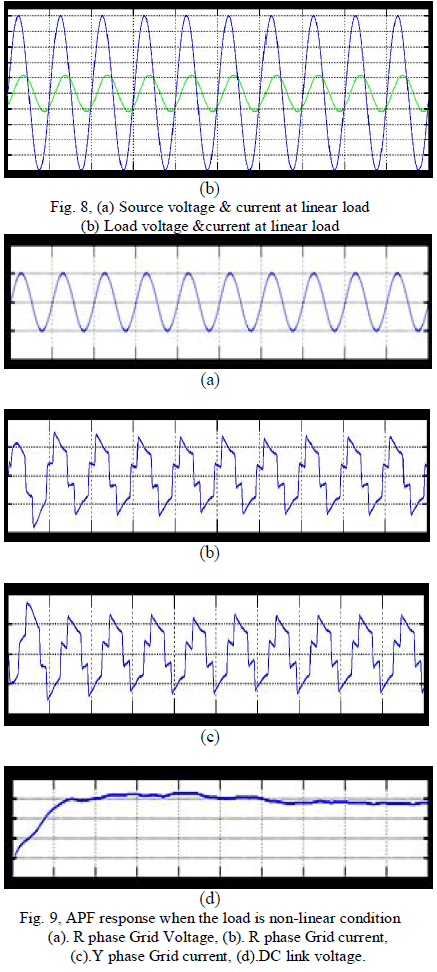
If consider the non-linear load condition at the time the following experimental result will be obtained, it’s shown in the fig. 9, and 10, from these graph when the load will be changed as non-linearly then the source side power flow will be non-linearly that is source side voltage and current is non-sinusoidal at the time the reactive power compensation is required. And the capacitor will be discharged for their minimum value. From these simulation result we can analyse the system performance of the overall power system network at non-linear load condition.

EXPERIMENTAL RESULT

To verify the effectiveness of the proposed method, an experimental setup was built and was tested under different conditions. The dc bus voltage has to be larger than the peak of the line to- line grid voltage, at the same time, it must be lower than the DG voltage VDG, and then the dc voltage Vr was set to 320V. The other parameters of the circuit are listed in Table I. A three phase rectifier fed a resistor in series with capacitor used as the nonlinear load and another resistor connected between A- and C-phase used as the unbalanced load. To demonstrate the proposed system as a power control station, an experiment was conducted. Fig. 7 and 8 shows performance of the DG interface with no local nonlinear load at VDG = 340V. It can be seen that the three-phase grid currents were sinusoidal and in phase with the grid voltages.an experiment with unbalanced nonlinear loads and no DG was conducted. Fig. 9 and 10 shows the waveform and spectrum of local nonlinear load currents. The three-phase load currents were unbalanced.

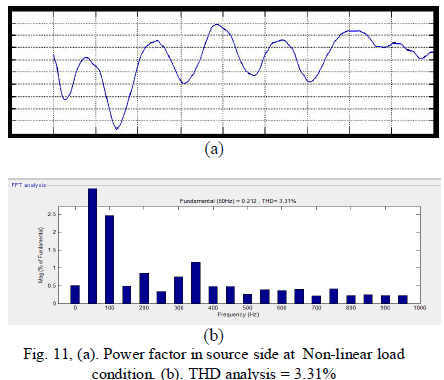From fig. 11 shows The grid current produced an almost-unity power factor of 0.98, and its total harmonic distortion (THD) was about 3.31%. In order to illustrate the load balancing and harmonic compensation capability of the proposed system as an APF.

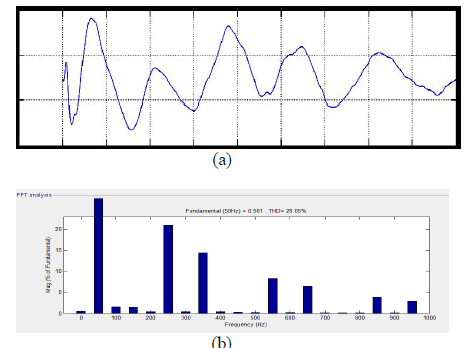Fig. 12, (a). Power factor in source side at Linear load condition, (b). THD analysis =28.05%.

From fig 12. Shows The grid current produced an the power factor was 0.83 and THD was 28.05% and the power factor of overall system was 0.98. To demonstrate the DG interface with dual functions, another experiment was conducted. To demonstrate the dynamic response of the proposed system, the VDG was changed from 320 to 360V and there was no local load.

CONCLUSION

A unified control method for the DG interface is proposed in this paper. The proposed method allows the utilization of DG to generate active power, eliminates harmonics, compensates reactive power, and mitigates load unbalance. Therefore, its multifunctional behaviour replaces the need for other power electronics compensators to enhance the performance of the distribution networks. With this proposed approach, to shape the grid currents into sinusoidal currents in phase with the grid voltage waveforms and with an amplitude depending on the power available from renewable sources. On the other hand the load harmonics current will reduced by injecting into the alternating current to system harmonic currents with an opposite phase. In this manner, controlling the dc voltage level can be equivalent to performing an active power balance for the whole system. As a result, there is a additional hardware and interface are not required. Experimental results verified the effectiveness of the proposed method.

References

Sangu Ravindra, Dr.V.C.Veera Reddy, and Dr.S.Sivanagaraju, “Design of Shunt Active Power Filter to eliminate the harmonic currents and to compensate the reactive power under distorted and or imbalanced source voltages in steady state” International Journal of Engineering Trends and Technology- Volume2Issue3- 2011.
Maoh-Chin Jiang “Analysis and Design of a Novel Three-Phase Active Power Filter” IEEE Transactions on Aerospace and Electronic Systems vol. 37, no. 3 July 2001.
Frede Blaabjerg, Marco Liserre, and Adrian V. Timbus, “Overview of Control and Grid Synchronization for Distributed Power Generation Systems” IEEE Transactions on Industrial Electronics, vol. 53, no. 5, October 2006.
Mukhtiar Singh, Vinod Khadkikar, Ambrish Chandra, and Rajiv K. Varma, “Grid Interconnection of Renewable Energy Sources at the Distribution Level With Power-Quality Improvement Features” IEEE Transactions on Power Delivery, vol. 26, no. 1, January 2011.
Y.-C. Kuo, T.-J. Liang, and J.-F. Chen, “A high-efficiency singlephase three-wire photovoltaic energy conversion system,” IEEE Trans. Ind. Electron., vol. 50, no. 1, pp. 116–122, Feb. 2003.
S. A. Gonzalez, R. Garcia-Retegui, and M. Benedetti, “Harmonic computation technique suitable for active power filters,” IEEE Trans. Ind. Electron., vol. 54, no. 5, pp. 2791–2796, Oct. 2007.
J.M. Carrasco, L. G. Franquelo, and J. T. Bialasiewicz, “Powerelectronic systems for the grid integration of renewable energy sources: A survey,” IEEE Trans. Ind. Electron., vol. 53, no. 4, pp. 1002–1016, Aug. 2006.
K. J. P. Macken, K. Vanthournout, and J. Van deneybus, “Distributed control of renewable generation units with integrated active filter,” IEEE Trans. Power Electron., vol. 19, no. 5, pp. 1353–1360, Sept. 2004.
M. Cirrincione, M. Pucci, and G. Vitale, “A single-phase DG generation unit with shunt active power filter capability by adaptive neural filtering,” IEEE Trans. Ind. Electron., vol. 55, no. 5, pp. 2093–2110, May 2008.
C. J. Gajanayake, D. M. Vilathgamuwa, P. C. Loh, R. Teodorescu, and F. Blaabjerg, “Z-source-inverter-based flexible distributed generation system solution for grid power quality improvement,” IEEE Trans. Energy. Convers., vol. 24, no. 3, pp. 695–704, Sept. 2009.
P.-T. Cheng, C.-A. Chen, T.-L. Lee, and S.-Y. Kuo, “A cooperative imbalance compensation method for distributedgeneration interface converters,” IEEE Trans. Ind. Appl., vol. 45, no. 2, pp. 805–815, Mar./Apr. 2009
P. Hsu and M. Behnke, “A three-phase synchronous frame controller for unbalanced load,” in Proc. 29th Annu. IEEE Power Electron. Spec. Conf., 1998, pp. 1369–1374.
M. I. Marei, E. F. El-Saadany, and M. M. A. Salama, “A novel control algorithm for the DG interface to mitigate power quality problems,” IEEE Trans. Power. Deliver., vol. 19, no. 3, pp. 1384– 1392, Jul. 2004.
Y. Li, D. M. Vilathgamuwa, and L. P. Chiang, “Microgrid power quality enhancement using a three-phase four-wire grid-interfacing compensator,” IEEE Trans. Ind. Appl., vol. 41, no. 6, pp. 1707– 1719, Nov./Dec. 2005.
H. S. Song and K. H. Nam, “Dual current control scheme for PWM converter under unbalanced input voltage conditions,” IEEE Trans. Ind. Elec., vol. 46, no. 5, pp. 953–959, Oct. 1999.
W. C. Lee, T. K. Lee, and D. S. Hyun, “A three-phase parallel active power filter operating with PCC voltage compensation with consideration for an unbalanced load,” IEEE Trans. Power Electron., vol. 17, no. 5, pp. 807–814, Sept. 2002.
Mi-Ching Tsai, and Wu-Sung Yao “Design of a Plug-In Type Repetitive Controller for Periodic Inputs” IEEE Transactions on Control Systems Technology, vol. 10, no. 4, july 2002.
S. A. Gonzalez, R. Garcia-Retegui, and M. Benedetti, “Harmonic computation technique suitable for active power filters,” IEEE Trans. Ind. Electron., vol. 54, no. 5, pp. 2791–2796, Oct. 2007.