International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

A Study of H -Function of Two Variables

Yashwant Singh1 Harmendra Kumar Mandia2
  1. Lecturer, Department of Mathematics, Government College, Kaladera, Jaipur, Rajasthan , India
  2. Lecturer, Department of Mathematics, Seth Moti Lal (P.G.) College, Jhunjhunu, Rajasthan, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

In the present paper, the author has introduced a new special function namely H -function of two variables in the literature of special functions. The definition, convergence, asymptotic behaviors have been considered. Next, we obtain some properties of H -function of two variables. Later on, the author establish a series representation for the H -function of two variables. Some interesting special cases of H -function of two variables by comparing the series representation of H -function of two variables and H -function of one variable is also established. In the last, the author has given two special cases of -function of two variables which are not the special cases of H -function of two variables. Key words: H -function, H -function of two variables, H -function, Series representation. (2000 Mathematics Subject Classification: 33C70)

Keywords
H -function, H -function of two variables, H -function, Series representation. (2000 Mathematics Subject Classification: 33C70)

INTRODUCTION
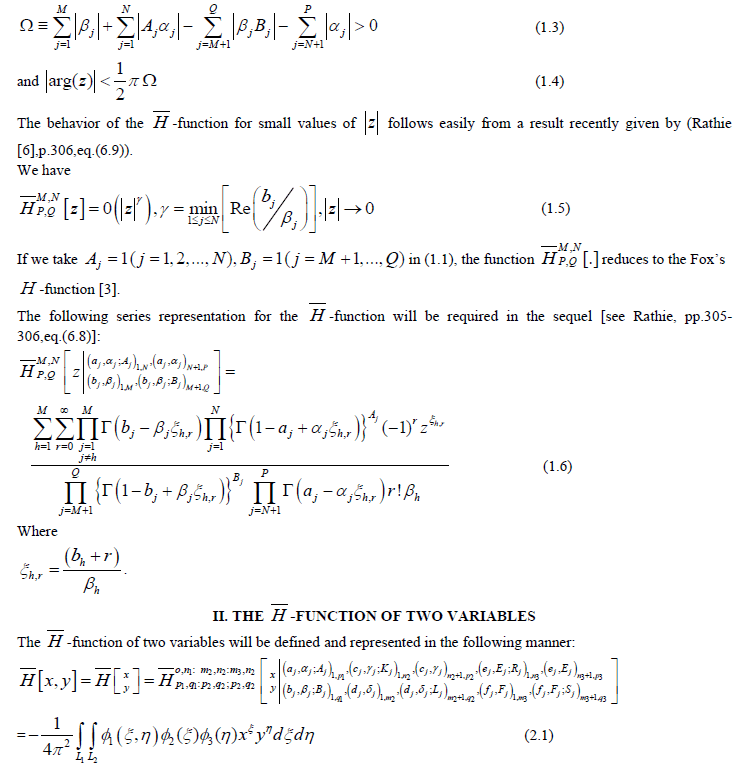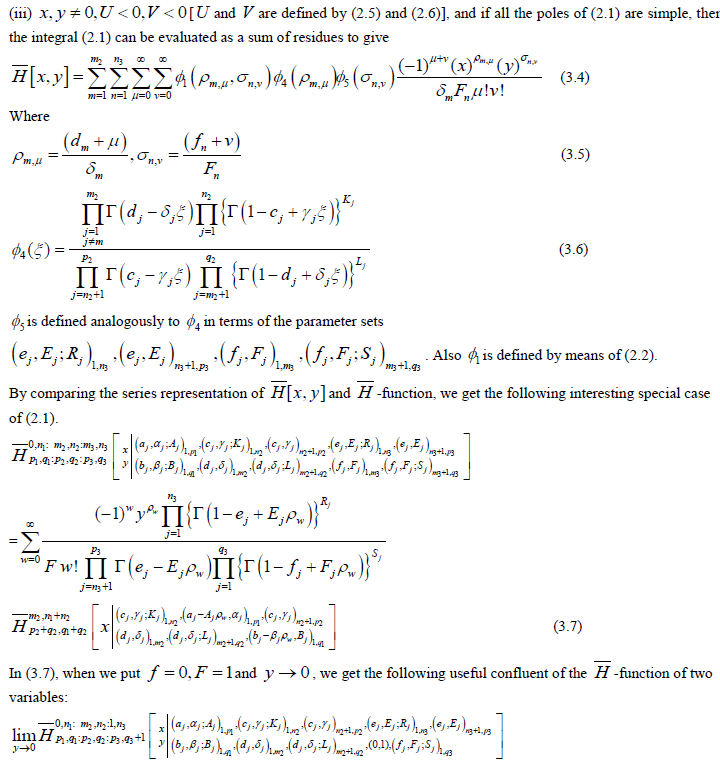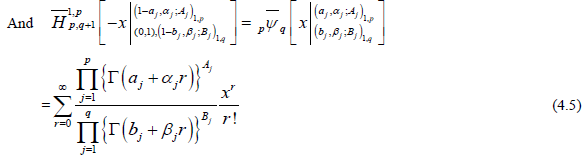image
image
image
image
image
image
image
image

References
  1. Buschman, R.G. & Srivastava , H.M.; The H -function associated with a certain class of Feymann Integrals. J. Phys. A. Math. Gen.:pp.4707-4710 ,1990.
  2. Erdelyi,A., Magnus, W., Oberhettinger , F and Tricomi , F.G.; Higher Transcendental Functions. Vol. I, McGraw-Hill, NewYork, 1953.
  3. Fox, C. The G and H -function as Fourier kernels. Trans. Amer. Math. Soc.98:pp, 395-429, 1961.
  4. Gupta ,K.C., Jain, R. and Sharma, A.; A study of unified finite integrals with applications. J. Rajasthan Acad. Phys. Sci. Vol.2(4):pp,269-282, 2003.
  5. Mittal, P.K. & Gupta, K.C.; An integral involving generalized function of two variables. Proc. Indian Acad. Sci. Sect. A( 75): pp, 67-73, 1961.
  6. Rathi, A.K. A new generalization of generalized hypergeometric functions. Le Mathematiche Fasc. II52:pp, 297-310, 1997.
  7. Srivastava, H.M. , Gupta , K.C. & Goyal,S.P.; The H -functions of One and Two Variables With Applications. South Asian Publishers, New Delhi,1982.