ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
A.Praveen Prakash1, Esther Jerlin J 2, Bennilo Fernandes J3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The quality of teaching and learning mathematics has been one of the major challenges and concern of the educators. Mathematics is often considered as a subject that a student either understand or doesn‟t, with little in between. In reality, mathematics comprises of wide variety of skills and concepts. Mathematics education should enable engineering students to communicate their ideas in an unambiguous and understandable way and should equip themselves with the analytical skills as practicing engineers. It is a collection of tools that can be used to solve certain well-defined problems. Mathematical thinking and modeling give engineers the ability to approach new problems with confidence. There are around 570 engineering colleges in Tamil Nadu where students show their aversion in learning mathematics and they learn this subject without interest. More number of arrears is kept in this subject compared to other subjects. Students fail to understand the seriousness of this subject. This paper analyses the various causes for the aversion by the engineering students in learning mathematics given by the teachers using Fuzzy Cognitive Map (FCM) model.
Keywords |
| FCMs, Hidden pattern, fixed point, aversion. |
INTRODUCTION |
| In modern world of science and technology mathematics plays a vital role. Mathematics is the indispensable tool for engineering curriculum. Its importance is noticed in all fields as called as Queen of Sciences. It is based on both logic and reality of the world. But how far this subject is concentrated by the students in engineering is a question mark. Mathematics is science of pattern that engineers have to seek out whether found in numbers, space, science, computers, imaginary abstractions, or elsewhere. Knowledge and understanding of basic mathematics have always been challenging criteria for the engineering students. The kind of less academic achievement in lower classes makes to have fear for the subject and it continues till the end. There are also various causes for the students to feel mathematics is a subject beyond their understanding and interest. The open statement given by most of the engineering students that number of arrears occurs only in mathematics which acts as a pathetic situation in this challenging and competitive world. |
II. LITERATURE SURVEY |
| There are many socio-economic problems existing in the world. For the real world problems Bart Kosko has illustrated the Fuzzy model FCM which are more applicable when the data is an unsupervised one. He tells that FCMs , model the world as a collection of classes and causal relation as a collection of classes. It works on the opinion of experts. W.B Vasantha Kandasamy explained the notion of FCM model in a simplest level and described each Fuzzy model using examples from real-world problem. Her book helps social scientists who are interested in finding out ways to emancipate the society. FCMs are used to model several types of problems varying from gastric-appetite behaviour, popular political developments etc. FCMs are also used to model in robotics like plant control.Her book consists of properties,definitions, strength and weakness of FCM model. For the study of political situation in any nation( i.e ) The prediction of electoral winner or how people tend to prefer a particular politician and so on and so forth involves not only a lot of uncertainty for this, no data is available. They form an unsupervised data. Hence she applied FCM model to Indian politics by taking an expert‟s opinion as six nodes (i.e) language, community, service to people, finance and media, party‟s strength and opponent‟s strength and finally working members for the party. Using these six nodes, several expert‟s opinion are obtained and found out the conclusion. |
III. FUZZY COGNITIVE MAP (FCM): |
| introduced by Bart Kosko in the year 1986.This work is based on expert opinion collected throughout Chennai. The data was collected and assimilated from the people using a linguistic questionnaire and this linguistic responses were transformed into fuzzy data. It is important to note that, while doing fuzzy mathematical models, the fuzzy matrix make take its entries from the interval [-1.1]. Even then, they are known as fuzzy matrices. Therefore, it is understood that Fuzzy tools alone have the capacity to analyze these concepts further substantiating the choice of this method.. This paper consists of five sections. First Section gives the information about fuzzy mathematical model. Second Section gives the preliminaries of FCM. In Section three, we give the description of the problem .In section four, we analyze the problems of the engineering students using FCM. Final Section gives the Conclusion based on our study. A. Preliminaries: Fuzzy cognitive maps (FCMs) are more applicable when the data in the first place is an unsupervised one. The FCMs work on the opinion of experts. FCMs model the worlds as a collection of classes and causal relation between classes. Definition 2.1.1: An FCM is a directed graph with concepts like policies, events etc as nodes and causalities as edges. It represents causal relationship between concepts. Definition 2.1.2: When the nodes of the FCM are fuzzy sets then they are called as fuzzy nodes. Definition 2.1.3: FCMs with edge weights or causalities from the set {-1, 0, 1} are simple FCMs. Definition 2.1.4: The edges eij take values in the fuzzy causal interval [-1,1]. eij = 0 indicates no causality, eij> 0 indicates causal increase Cj increases as Ci increases (Or Cj Decreases as Ci Decreases). eij< 0 indicates causal decrease or negative causality. Cj decreases as Ci increases (and or Cj increases as Ci decreases). Simple FCMs have edge values in {-1, 0, 1}. Then if causality occurs, it occurs to a maximal positive or negative degree. Simple FCMs provide a quick first approximation to an expert stand or printed causal knowledge. If increase (Or decrease) in one concept leads to increase (or decrease) in another, then we give the value 1.If there exists no relation between the two concepts, the value 0 is given. If increase (or decrease) in one concept decreases (or increases) another, then we gives the value -1. Thus, FCMs are described in this way. Consider the nodes or concepts C1, …, Cn of the FCM. Suppose the directed graph is drawn using edge weight eij {0, 1, -1}. The matrix E be defined by E= (eij ), where the eij is the weight of the directed edge Ci Cj. E is called the adjacency matrix of the FCM, also known as the connection matrix of the FCM. It is important to note that all matrices associated with an FCM are always square matrices with diagonal entries as zero. Definition 2.1.5: Let C1, C2,…. Cn be the nodes of an FCM. Let A=(a1, a2,…., an ), where ai {0,1}. A is called the instantaneous state vector and it denoted the on off position of the node at an instant ai =0 if ai is off andai=1 if ai is on, where i = 1, 2, …, n. Definition 2.1.6: Let C1 , C2 , …, Cn be the nodes of an FCM. Let C1 C2, C2 C3, …, Ci Cj, be the edges of the FCM (i j). Then, the edges form a directed cycle. An FCM is said to be cyclic if it possesses a directed cycle. An FCM is said to be acyclic if it does not possess any directed cycle. Definition 2.1.7: An FCM with cycles is said to have a feedback. Definition 2.1.8: Where there is a feedback in an FCM, i.e., When the causal relations flow through a cycle in a revolutionary way, The FCM is called a dynamical system. Definition 2.1.9: Let C1C2, C2 C3,…, Ci Cj, be a cycle when Ci is switched on and if the causality flows through the edges of a cycle and if it again causes Ci, We say that the dynamical system goes round and round. This is true for any node Ci, for i = 1, 2, …, n. The equilibrium state for this dynamical system is called the hidden pattern. Definition 2.1.10: If the equilibrium state of a dynamical system is a unique state vector, then it is called a fixed point. Consider a FCM with C1, C2, …, Cn as nodes. For example let us start the dynamical system by switching on C1. Let us assume that the FCM settles down with C1and Cn on, i.e. the state vector remains as (1, 0, 0,…, 0, 1) this state vector (1, 0, 0, …, 0, 1) is called the fixed point. Definition 2.1.11: If the FCM settles down with a state vector repeating in the form A1 A2 … AI A1. Then this equilibrium is called limit cycle. |
IV. A STUDY ON THE CAUSES FOR AVERSION TO MATHS EXPERIENCED BY ENGINEERING STUDENTS USING FCM MODEL |
| By administering linguistic questionnaire and the expert‟s opinion we have taken the following ten concepts {C1, C2, ..., C10} A. The problems faced by the engineering students in India: The problems faced by the engineering students in Tamil Nadu are taken as the concepts and as the main nodes for our analysis. They are listed as follows: C1- Memory loss C2- Attention loss C3- Lack of sufficient knowledge in basics C4- Lack of sufficient application skills C5- Lack of interest in unitizing sufficient time C6- Lack of confidence C7- Health problem C8- Lack of sufficient practice C9- Peer group pressure C10-Lack of logical reasoning power &Analytical skill |
| C1. Memory loss: Memory plays a significant role among the students in learning mathematics. They find hard to remember all the basic rules, steps and formulae in storing, recalling and reproducing in their examination. Memory loss may be due to their individual health condition, sleep deprivation, indulging in drinking, other distractions etc. Memory plays a vital role on thinking with numbers. C2. Attention Loss Students with attention deficit disorder have particular problem like they fail to remain focused while learning. They appear to be „dreamy‟ and pay no attention. They easily get distracted, lose their concentration and miss to listen how the problem is solved. Thus they have poor listening skills and miss the key points. C3. Lack of sufficient knowledge For student, content knowledge is crucially important to the improvement in learning mathematics. Thorough knowledge in content makes the student to think, reason out and apply in the asked problem. Lack of sufficient knowledge makes the student to skip out the example problem and thus creates fear among them. While Studying, XI and XII portions are not covered properly in many of the schools. Though, they score high marks in XII, they lack knowledge of the fundamentals that they should have learnt in XI. C4. Lack of sufficient application skill On knowing the content knowledge does not tell that the students are well-versed in subject. Their application skill proves their content knowledge in learning mathematics. If the student do not understand the content well then they are not good at employing steps to solve the problem. Thus they lose their confidence level. The problem may emerge even if the teacher fails to teach the application part of the theory he teaches. C5.Lack of interest in utilizing time As the proverb says „Time is precious‟ and „Time and Tide waits for no man‟ students who do not value the worth of time, face many problems. They fail to pay attention in class, remembering the concepts and in analyzing the problems. Due to the influence of media and peer- group pressure they indulge in various immoral and unwanted activities and waste their time. They finally regret for the time lost. C6.Lack of confidence Confidence plays a vital role not only for the students but for each and every individual to face the unexpected problems occurs in the world. Students who lack confidence level, experience fear and try to escape from learning, recalling and applying them to solve the problem. The confidence level can be activated by giving continuous coaching, friendly interaction with the students and paying attention to them. C7.Health Problems Most of the students lack in memory power, paying attention to the class, lack of interest in subject due to deficits in their health condition. There are students who spoil their healthy life style by taking drugs, alcohol and involving other illegal activities. As a result they lose their concentration in studies. Family background also plays a major role in affecting both physical and mental fitness of the students. C8.Lack of sufficient practice Students who fail to practice often experience failure in mathematics. They just think that having the content knowledge is just enough and face their examination without practicing. A small alteration in question format will pose a big problem to such a students. Naturally they fail to answer the question even if it is a simple one. “Practices make a man perfect”. Only while practicing, knowing, understanding, recalling the concepts occurs. The worth of utilizing the time in practice results in good performance. C9.Peer-group pressure Society consists of many relationships. Friends play the vital role in teen –age period. Peer-group pressure distracts the individual both in good as well as in bad way. It is up to the individual who decides the way to choose. Most of the engineering students keep arrears in mathematics due to their peer group pressure who involve in wrong activities like mass bunking, drugs, alcohol addiction, and love affairs etc. which make them to consider the subject as bore and fail to be present in the class. Instead they enjoy those hours in canteen, beach or cinema, etc. Student at this age get affected a lot by peer-group pressure. C10. Lack of logical and learning: It involves the students to think and monitor their learning. Students should be motivated from the beginning to justify their answers like why such steps take place and what is involved in carrying those steps. Lack of such criteria makes the student to memorize the steps which they don‟t understand. Thus they lack in application skill and lose confidence to attend any unfamiliar problem. For this the teacher should reinforce the students with different illustrations while teaching. B. Method of Determining Hidden Pattern Let C1, C2, …, Cn be the nodes of an FCM, with feedback. Let E be the associated adjacency matrix. Let us find the hidden pattern when C1 is switched on. When an input is given as the vector A1= (1, 0, 0, …, 0), the data should pass through the relation matrix E. this is done by multiplying A1 by the matrix E. Let A1 E= (a1,…., an)with the threshold operation that is by replacing ai by 1 if ai> k and ai by 0 if ai<k (k is a suitable positive integer). We update the resulting concept. The concept C1 is included in the updated vector by making the first coordinate as 1 in the resulting vector. Suppose A1 E A2 then consider A2 E and repeat the same procedure. This procedure is repeated till we get a limit cycle or a fixed point. |
| C. Analysis of the Problem Using the linguistic questionnaire and the expert‟s opinion we have taken from the experienced teachers following ten concepts {C1, C2, ..., C10} as nodes. C1- Memory loss C2- Attention loss C3- Lack of sufficient knowledge in basics C4- Lack of sufficient application skills C5- Lack of interest in unitizing sufficient time C6- Lack of confidence C7- Health problem C8- Lack of sufficient practice C9- Peer group pressure C10-Lack of logical reasoning power &Analytical skill Now we proceed on to analyze the problems using FCM. Let us consider the ten concepts {C1, C2, ..., C10} |
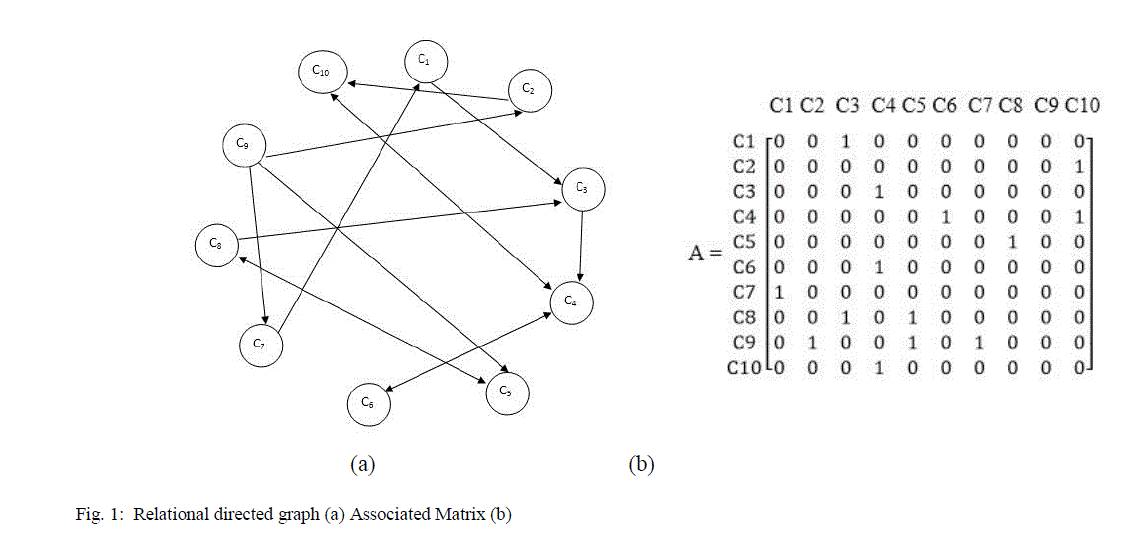 |
| Now using the matrix A of the Fuzzy Cognitive Map (FCM) the on state, we determine the hidden pattern. Suppose the concept C1 is in the on state and another nodes are in the off sate. |
 |
V. CONCLUSION AND SUGGESTIONS |
| While analyzing FCM, when the concept C8 “LACK OF SUFFICIENT PRACTICE” is kept in the on state, the other concepts C3, C4, C5, C6, and C10 are also in the on state. When the concept C4 “LACK OF SUFFICIENT APPLICATION SKILL” is kept in the on state, the other concepts C6, C10 are also in the on state. When the concept C2 “ATTENTION LOSS” is kept in the on state, the other concepts C4, C6, C10 are also in the on state. These ten attributes are inter-related to each other for the causes for aversion by engineering students in studying mathematics. This implies that one should exercise self-discipline and concentrate in learning the subject Math‟s. The Teacher must come well prepared to the class and facilitates the learning process by adopting innovative methods. The Institution should provide the necessary infra-structure facilities function like the “Smart Classroom”, “In-service course to the teacher”, well equipped library and laboratory and room.Above all the parents must provide a congenial atmosphere in the house and keep in motivating their children‟s in their studies. |
References |
|