International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

A Theoretical Study of Internal Pressure And Free Volume for Single Molecule of a Sample Liquid

D.Prakash and Dr. A.Mukunthan
  1. Department of Physics, Bharath University, Chennai – 600073, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

In the current research work a sample liquid is taken and attempt has been made for it to drive expressions for internal pressure and mean free volume occupied per molecules which depend up on the packing of molecules. Thermodynamical parameters like entropy, volume and temperature liquid property like viscosity are considered for deriving the expression of internal pressure. For the expression of free volume per molecule liquid properties like viscosity and the formula given by C.S.Suryanarayana &et.al are used. The free volume plays an important role in the propagation of ultrasonic waves in liquid.

I.INTRODUCTION
A sample liquid is taken and theoretical attempt has been made to derive expressions for internal pressure and free volume per molecule. The thermodynamic parameters sample like entropy, volume and temperature liquid properties like viscosity are considered for evaluation of expressions successfully.

II.THERMODYNAMICAL EQUATION STATE:
Thermodynamic importance of internal pressure is shown by bringing out its quantitative relationship with entropy and the partition function of the system. Internal pressure is shown to be related to the transport properties in liquids and solutions. The free energy of activation in the rate equations of Erring is almost the same as the cohesive energy of the system. In all rate processes, physical or chemical the energy barrier to be got over is just the cohesive energy barrier of the system in equilibrium.
The concept of free volume is a generalized aspect of the idea that its neighbors in a cell enclose each molecule. The free volume is broadly defined as the averages volume in which the center of the molecule can move inside the hypothetical cell due to the repulsion on the surrounding molecules.
The variation of entropy with volume and temperature may be represented in general terms as
At constant temperature, the first term is zero. Using Maxwell relation and for
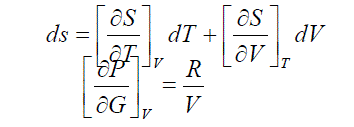image
image
Equ.(5) applies to a gas which is ideal. The problem now is to adapt it to liquids. This equ.(5) has a basic statistical interpretation in terms of the effect on the entropy of the larger volume available to each molecule as the pressure decreases. At constant temperature, the distribution of molecules among the possible vibration, rotational and electronic energy states is fixed and independent of pressure. So the only source of entropy change is the variation with the volume or pressure of the number of positions in space and the number of possible transnational energy levels opens to each molecules.
Statistically the entropy of an assembly of molecules forming thermodynamic systems is given by the equation.
image
Where W is the thermodynamic probability. W is the number of possible ways of distributing the molecules, among the various positions and energy levels available, which will lead to the observed state of the system. The entropy becomes less in a condensed phase as the free space is less than in a gas. Another important step in adapting equ.(5) to condensed phases consists in using for the volume V, the free volume Vf.
Newton and Eyeing [1] and also Len nard-Jones and Devon shire [2] expressed the entropy of vaporization as approximately
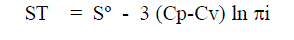image
Where Vg is the volume of the vapour and Vf the free volume of the liquid. Vf is the characteristic property of a liquid.
A discussion of the importance of free volume in liquids by Rice [3] Franks [4] and Franks & Evans [5] and Hirschfelder et al. [6] shows the validity of introducing Vf in place of V in Equ.(5).
Hirsch elder et al. used the viral theorem to calculate the free volume of a molecule in a liquid. Assuming that the average force acting on a molecule is the sum of the internal pressure and the external pressure P, times the area of a face of the cube they obtained,
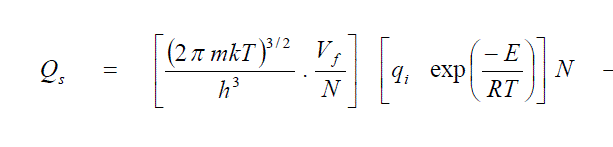image
In Equ. (8), k is the proportionality factor, d the collision diameter of the molecules times a constant depending on the type of packing of the molecules. This relationship is very important since it shows that the free volume of a molecule at a particular temperature and pressure depends only on the internal pressure of liquid in which it is immersed. Hirsch elder et al. found that the proportionality factor k was 2 for normal liquids. Hence Eqn. (5) can be written as applicable to liquids. Hence Eqn. (5) can be written as applicable to liquids by replacing R by (Cp-Cv) as
image
The fundamental importance of this equation is very clear when the entropy is seen to be a function of internal pressure in a liquid. The constant Sº will be the entropy at unit internal pressure πi is quantitatively related to the entropy of the medium by equ. (9) Even any microscopic changes occurring in the medium either due to molecular orientations or temperature changes should show up in a corresponding change in the internal pressure of the medium.
Internal pressure is more fundamental than the latent heat of vaporization and has the advantage that in multicomponent systems it is the internal pressure of the entire system that counts, and is easily visualized in comparison with the latter which gets complicated when dealing with mixtures. It is obvious that the behavior of a is just related straight to the overall internal pressure of the medium. The molar free volume of a liquid in equilibrium with its vapor.
Batschinsky[7] McLeod [8] Hildebrand [9] Hildebrand and Larnoreause [10] showed that viscosity, the most important intrinsic property of a liquid is quantitatively related to its free volume.
In the study of the thermodynamic properties of liquids, some of the properties are employed to derive the other. It is reasonable to represent the configuration integral in the form
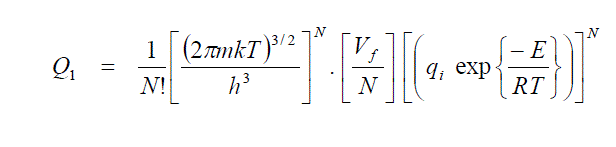image
Equ.(11) represents the partition function for solid and Eqn.(12) refers to that of a liquid. The increase in the entropy accompanying melting is merely due to the postulates that the whole of the free volume is available to each; molecule is the liquid stats, whereas in the solid the molecule is restricted to its own cell. For this reason the entropy change per mole arrived at in this manner is called the communal entropy. The changes from solid to liquid does not involve a sudden transition from complete restriction to complete freedom of movement of the molecules accomplished by the introduction of the whole of the communal entropy.

III.DETERMINATION OF FREE VOLUME IN LIQUIDS:
For the calculation of free volume we adopt the method where the potential field is uniform within the cell but rising very sharply at the boundaries.
For simplicity, let us suppose that there is cubic packing of the molecules in the liquid, one molecule may be considered as oscillating about the origin and the six nearest neighbors are regarded as being fixed in their mean positions along the three axes.One of these axes is represented in Fig.(1).
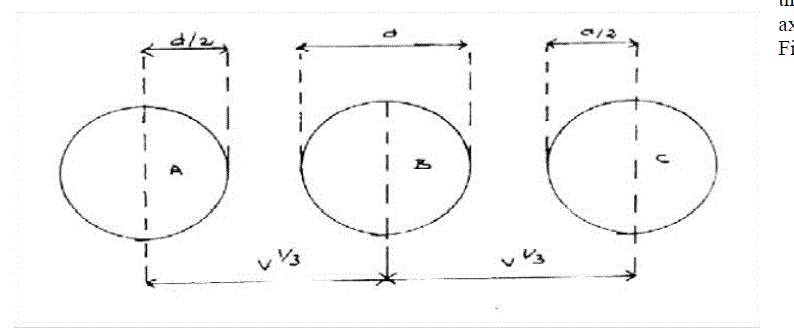image
Figure.1.
If V is the mean volume per molecule in the liquid, then each molecule is at a distance V1/3 from the origin. If d is the incompressible diameter of the molecule, (2 V1/3 – 2d) is the distance, the central atom is free to move along each axis and the free volume per single molecule is given by
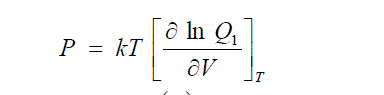image
As far as liquids are concerned, the Equ. (18) has tremendous significance. Originally, U in Eqn. (11.a) meant a potential function depending on the configuration of the molecules. This U is replaced by a mean value E per mole, averaged over all accessible configurations. The internal degrees of freedom of molecules do not contribute to the potential function. Hence from the thermodynamic Eqn. (12) it is clear that the variation with respect to volume of the averaged potential function E, which is basically the potential energy of interactions at a given temperature, is replaceable in condensed phases by the variation of internal energy E with volume at the same temperature.
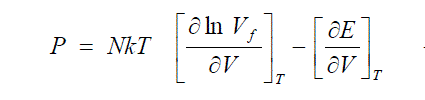image
This equation has some unique characteristics. This is an important equation connecting quantitatively Vf and V in liquid systems. Again this gives a second confirmation of Hirchfelder et al [6] who first showed that the free volume of a molecule at a particular pressure of a liquid in which it is immersed.
In Eqn.(11) the molecules in solids are assumed to be localized whereas in Eqn. (12) giving the partition function for a liquid, the molecules are not localilsed but the entire free volume is available for them. Thus the free volume available in a liquid system may be called the communal free volume. Hence any change in the communal free volume Vf apart from situations analysed by Gurney [11,12] and Wood [13] will be an indication of change in the entropy of the system.
2. Internal Pressure, Free Volume and Sound Velocity:
The velocity of sound for liquids is 5 to 10 times greater than the average velocity predicted by the Kinetic theory of gases. Suppose there are three molecules A, B and C in a line, and the wave front travels from the inner edges of B with a velocity of sound Ug Applicable to an ideal gas, then
Where τ is the ratio of specific heats of the gas and M is its molecular weight. As A collides with B, however, the signal is transmitted almost instantaneously to the opposites edges of B.
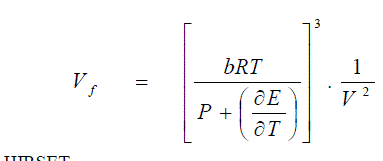image
Thus although the wave front moves apparently through the distance V1/3, it effectively travels a distance Vf1/3 as seen in the above Fig.
In the case of gases Vf1/3 , is not too different from V1/3 and in the case of solids Vf1/3 is far too small compared to V1/3. There are essential differences in the manner in which transverse stresses is propagated through gasses and solids. In a liquid, momentum is transferred partly by the diffusion as in gases, which is a relatively slow process, and partly by transverse elastic waves as in crystals, which is an extremely rapid process and the effective viscosity depends on their relative contributions. Thus the free volume plays an important role in ultrasonic propagation in liquids, and Vf1/3 is very small in the case of solids. The relation between free volume and viscosity has been derived by Bingham [14] and McLeod [8].
Liquids are characterized by viscous relaxation when subjected to ultrasonic radiation. In other words, material response by way of round propagation to mechanical stress signified by ultrasonic irradiation is not instantaneous but the two are separated by a time interval, which is about the same as viscous relaxation time. Thermal relaxation is negligible during sound propagation in liquids.
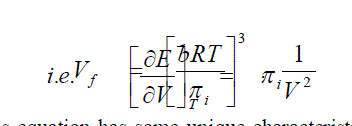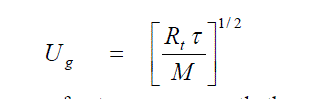image
image
involved in determining the internal pressure of a liquid by other methods, Eqn.(28) is reliable. This is the first equation involving easily measurable quantities, which are fundamentally responsible for the structure of a liquid or a solution.

IV.CONCLUSION
Theoretical expressions for internal pressure and free volume per unit molecules have been successfully eveluatede by considering thermodynamical properties like entropy, volume and temperature liquid property like viscosity. The values obtained for the internal pressure and free volume per molecule ion the present work coincide with values obtained in the literature available showing the validity of the present work.

ACKNOWLEDGEMENT
The authors are very thankful to Hon., Chairman, Chancellors, Vice-Chancellor, Director and Dean (Enge) and Dean R&D of Bharath University for their continuous support and encouragement given to bring out this paper.

References
  1. Newton, R.F. & Eyring H., Trans.Faraday.Soc.33-73(1937 V,4,111-119(1977)
  2. Leonard – Jones, J.E.: Proc. Roy.Soc.A.106, 463 (1924)
  3. Rice. O.K., J. Chem. Phys., 5 353 (1937).
  4. Frank, S.H., Barker, J.A. J.Chem. Phy., 13 473, 493 (1945).
  5. Frank, S.H. & Evans, M.W., J. Chem. Phy., 13 507 (1945).
  6. Hirschfelder J.E.,Stevenson, D.P.&Eyring: J.Chem.Phy.5, 901(1937)
  7. Batschinski A.J.Z Phy Chem. (Germany), 84,643 (1913)
  8. Mccleod D.B., Trans Faraday SOC (GB) 41,771 (1945)
  9. Hildebrand JH, Science (USA), 174 490 (1971).
  10. Hidlebrand Jh & Lamereaus Rh. Proc Natl Acad Sci (USA) 69, 3428 (1972)
  11. Gurney, R.W.: Introduction to Statistical mechanics, Chap.7, McGraw Hill (1949).
  12. Gurney, R.W.: Ionic process in solution, chap.3 McGraw Mill (1953).
  13. Wood, Scott, E., Brusic.: J.Am. Chem.Sec. 65, 1891 (1943).
  14. Bingham, E.C. Fluidity and Plasticity, McGraw Hill, (1922).
  15. Suryanarayana, C.V. Kuppusamy, J.J ACoust SOC. Ind.9 759 (1976)