International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Absorption of Chlorine into Aqueous Sodium Hydroxide System

K. S. Agrawal
 Assistant Professor, Department of Chemical Engineering, Faculty of Technology and Engineering, The M. S. University of Baroda, Vadodara, Gujarat, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The absorption of chlorine into aqueous hydroxide solutions is one of the important systems having industrial importance and also is of theoretical interest. Danckwerts (1950a and 1950b),Sherwood and Pigford (1952), Brian et al. (1965), Hikita et al. (1972), Hikita et al. (1973 ) and Takahashi et al. (1967) have studied the gas absorption using mathematical models. In this paper, we have developed a mathematical model and analyzed the experimental data obtained by us and Hikita et al. (1973) on the basis of the penetration theory for gas absorption accompanied by a two step instantaneous chemical reaction. In this work, the rate of absorption in the jet ejector is studied by using 𝐶𝑙2 aqueous 𝑁𝑎𝑂𝐻 system at 300𝐶

Keywords
Absorption of chlorine, Jet Ejector, Interfacial Area, Absorption rate, Mathematical Modeling, Finite Difference Method

INTRODUCTION
Danckwerts (1950a and 1950b) and Sherwood and Pigford (1952) showed that absorption rate could be predicted by the penetration theory for absorption accompanied by an instantaneous irreversible reaction of the type + → . Spalding (1962) studied the absorption rate of 2 into water and aqueous solutions of 24 and using liquid-jet column. They have also established that the absorption rate of 2 will be affected by the reactions (1) and /or (2):
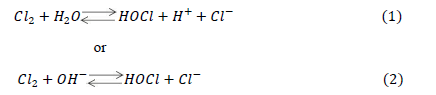image
depending upon the value of the solution. Further, they have observed that when value was higher than 12.6 (i.e. − concentration more than 0.04/ the forward part of reaction (2), was rate-controlling and the effect of this reaction on the absorption rate could be predicted by the penetration theory for absorption accompanied by an instantaneous irreversible reaction. Brian et al. (1965) studied gas absorption accompanied by a two-step chemical reaction, + → followed by + → . They have considered both steps irreversible and of finite reaction rates and presented the theoretical analysis based on both, the film theory and the penetration theory, with numerical solutions for the reaction factor, . Takahashi et al. (1967) used two different types of absorbers viz. liquid-jet column and a stop-cock type absorber to study the absorption rates of 2 into aqueous (0.05 0.2 /). The predicated absorption rate using penetration theory was in good agreement with experimental results. Hikita et al. (1972) studied gas absorption of two-step chemical reaction, + 1 followed by + 2 , accompanied by + 2. They have studied the effect of chemical equilibrium constant ratio, P (which is defined as 1 2), on reaction factor, β. They have developed mathematical models for = 0, finite value and ∞, for equal diffusivity and unequal diffusivities of species on the basis of penetration theory.
Hikita et al. (1973) stated that in case of strong hydroxide solution the forward part of reaction (2) is not only reaction which governs the absorption rate of 2 but the rapid reaction
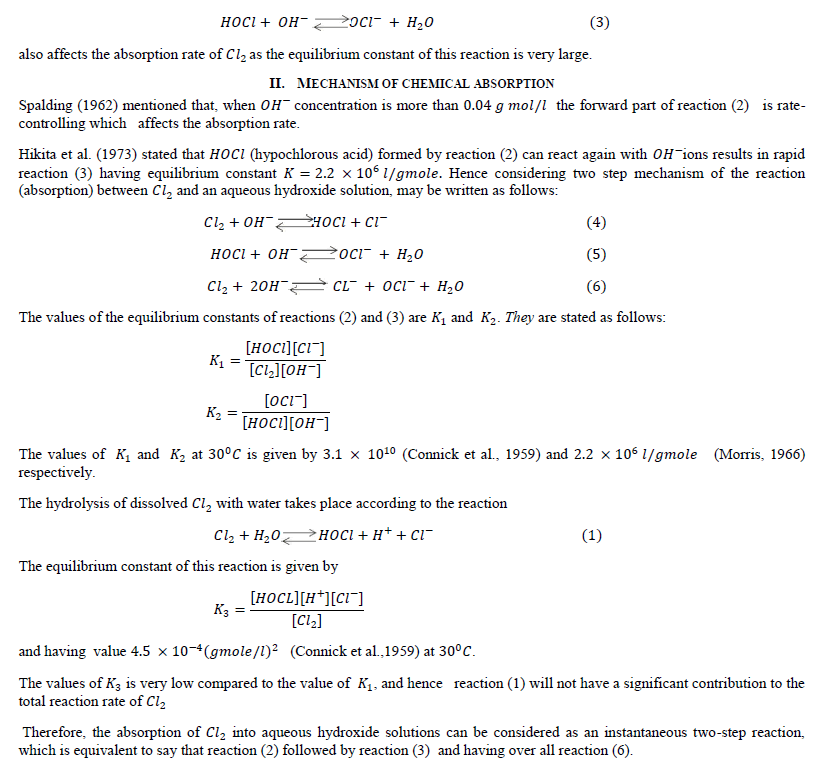image

III. MATHEMATICAL MODELS RELATED TO ABSORPTION
rate of absorption of reactant (gas) with instantaneous chemical reaction can be predicted by summing (a) Amount of A diffuse away unreacted and (b) Amount of reacted (in the form of ) diffuse away from the gas-liquid interface.
image
image
image
The diffusion of all species, based on the penetration theory is modeled by partial differential equations. The concentration profile for each species which will be derived by solving the developed model will be similar to that as shown in Figure 1.
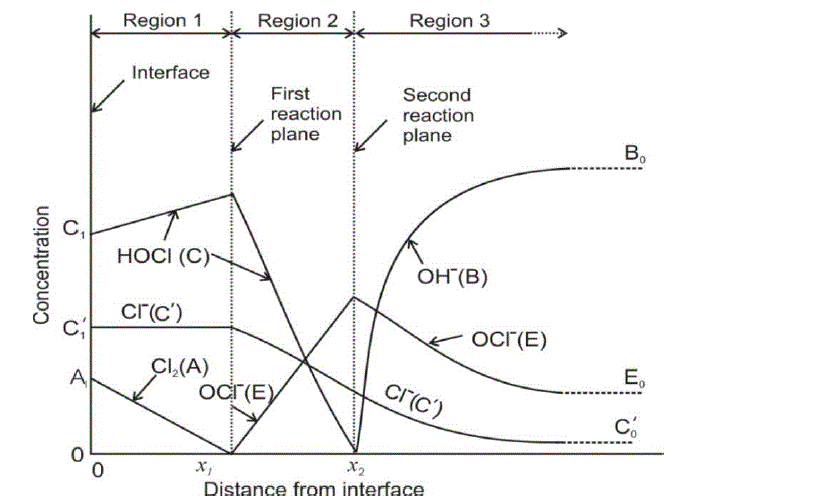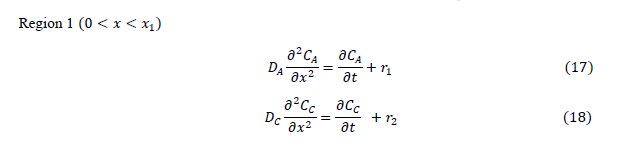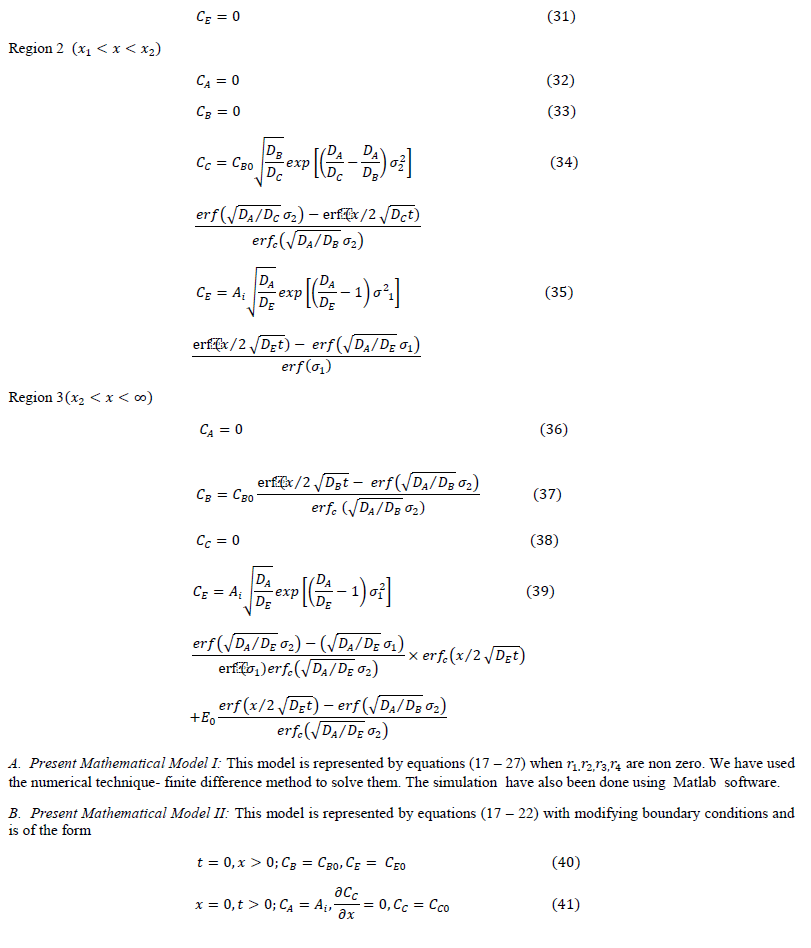image
image
image
images
image
image
The following results may be drawn from figure (2).
The lines in the figure having higher are at higher position for the same . This indicates that at higher ratio of diffusivities of reactants (liquid and gas), the enhancement factor is higher. It can be concluded that higher the diffusivity of liquid reactant with respect to gaseous reactant, higher is the enhancement factor. The increase in enhancement factor is due to reduction in thickness of interfacial film. The reduction in thickness in interfacial film is due to movement of reactant is faster toward interface compared to movement of 2 toward bulk of liquid.
For same plots shows that enhancement factor increases with increase in the reactant ratio ( ). The increase in enhancement factor is steeper at initial increase of . After that the rate of rise in enhancement factor with respect to rate of rise in reactant ratio is reducing and after certain value of , there is hardly any rise is enhancement factor with respect to reactant ratio. It can be concluded that there is increase in enhancement factor with increase in liquid reactant concentration up to certain limits. This may be taken to mean that at higher 0 enhancement factor is higher. The reduction of at higher is due to high viscosity of solution at higher 0.
For the same ratio of the value of enhancement factor derived from proposed mathematical model II is higher than the value from proposed mathematical model I. The value derived from Hikita (1972) is the lowest. The predicted values from proposed mathematical model I and proposed mathematical model II are higher than Hikita (1972) as the effect of diffusing out have been considered.
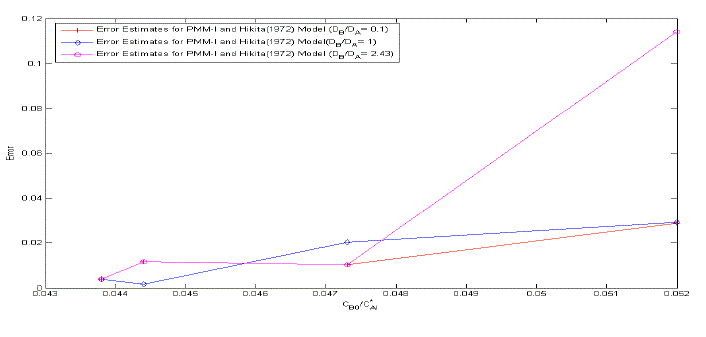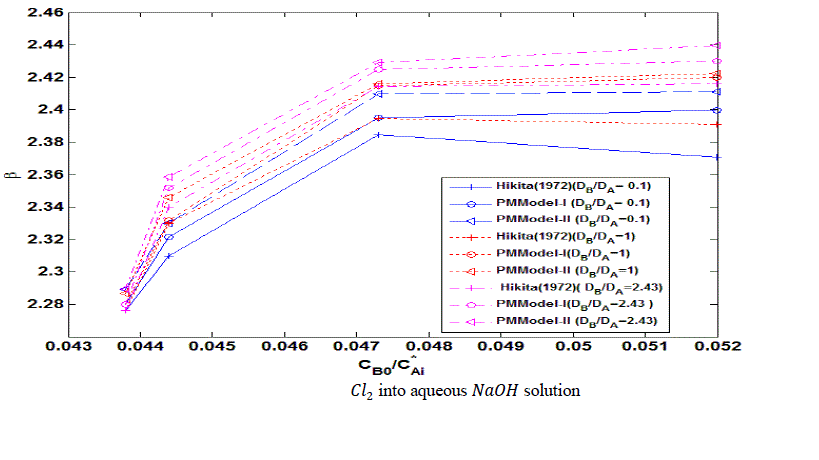
image
The error estimates between Hikita (1972) model and proposed mathematical model I is shown in Fig. 3. The error is defined as = 2.43, 1 ,0.1 It is observed that the lower value of for different , the proposed mathematical model I and Hikita (1972) model are comparable. However, for higher values of , the comparison shows that there is a numerical instability in Hikita (1972) model (higher value of error). Therefore, we conclude that the proposed model I is well-posed. B. Comparison of experimental results with simulated results Figure (4) is a comparison of predicted by the simulated results of Hikita (1973), proposed mathematical model I and proposed mathematical model II with experimentally determined values ( for = 0.602 10−3 3 ) at actual value of diffusivity ratio: = 2.32, = 1.04′ = 1.4 and = 0.786 (Table A 3.4). It may be observed that the values obtained by experiment, Hikita (1973) model and proposed model I are comparable. Equations (17) to (22) and (45) to (50) indicate that is a function of rate of reactions and three diffusivity (in liquid) ratios, and. The predicted values by proposed mathematical model I are higher to some extent than Hikita (1973) model which is due to the effect of reaction on , have been consider in mathematical model I. It may be make out that the influence of rate of reaction are marginal that may be because being instantaneous reaction diffusivity ratio of species are rate controlling.
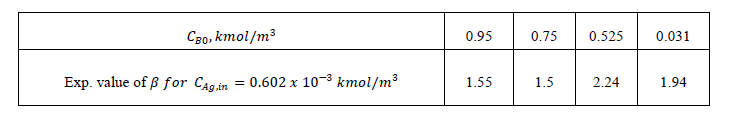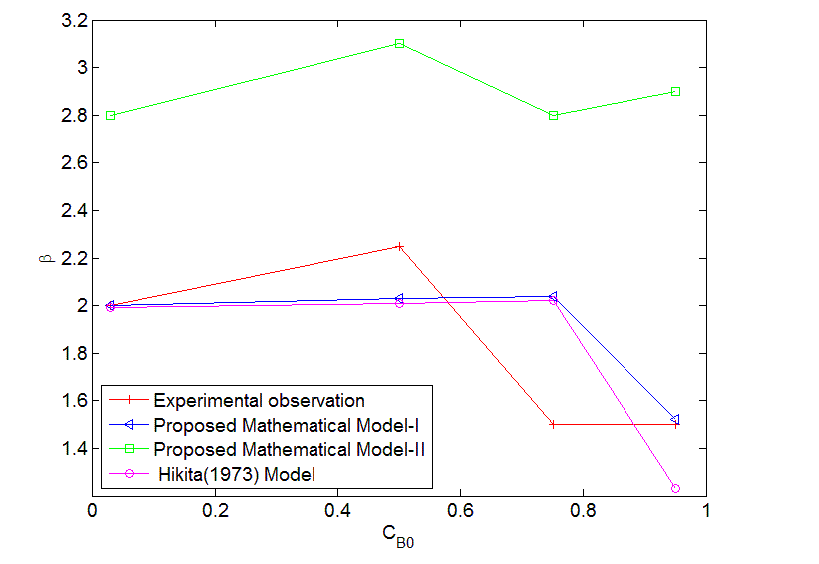image
image
The values predicted by proposed mathematical model II for are higher than experimental values. It may be concluded that the effect of jumping in the concentration of and − which have been considered in the model at the interface 1 and 2 are not appreciable. Hence the values predicted by model II are higher. So model II is not appropriate under operating conditions of the experiment.

V. CONCLUSION
image

References
  1. P. L. T. Brian and M. C. Beaverstock, Chem. Eng. Sci, 20, 47, 1965.
  2. A. E. Connick and Y. T. Chia, “The hydrolysis of chlorine and its variation with temperature”, J. Am. Chem. Soc., 81, pp. 1280, 1959.
  3. P. V. Danckwerts, “Absorption by simultaneous diffusion and chemical reaction”, Trans. Faraday Society, 46, pp. 300, 1950a.
  4. P. V. Danckwerts, “Unsteady-state diffusion or heat conduction with moving boundary”, Trans. Faraday Society, 46, pp. 701, 1950b.
  5. H. Hikita, S. Asai and T. Takatsuka, “Gas absorption with a two-step instantaneous chemical reaction”, The Chemical Engineering Journal, 4 (1), pp. 31-40, 1972.
  6. H. Hikita, S. Asai, Y. Himukashi, and T. Takatsuka, “Absorption of chlorine into aqueous sodium hydroxide solutions”, Chemical Engineering Journal,, 5, pp. 77-84, 1973.
  7. J. C. Morris , “The Acid Ionization Constant of HOCl from 5° to 35°”, J. Phys. Chem., 70, pp. 3798, 1966.
  8. T. K. Sherwood and R. L. Pigford, Absorption and Extraction, 2nd Edn., New York, McGraw-Hill, 1952.
  9. C. W. Spalding, “Reaction kinetics in the absorption of chlorine in to aqueous”, A.I.Ch.E.J., 8, pp. 685, 1962.
  10. T. Takahashi, M. Hatanaka, and R. Konaka, “Absorption of chlorine into still liquid in a simple stop-cock type absorber”, Can. J. Chem Engrs, 45, pp. 145, 1967.