ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
S. Prabu1, S.K. Rajesh Kanna2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In general, tool life and surface finish are the important aspects considered in evaluating the performance of a machining process. In this research, increased tool life with better surface finish has been obtained by using TiAlCn nano-coated cutting tool for turning operations. TiAlCn nano-coating has made on the turning tool by the process of chemical vapor deposition (CVD) and have been used to machine the mild-steel work-piece by varying cutting parameters namely spindle speed, feed rate and depth of cut to identify the machining characteristics namely tool wear rate and surface finish. The obtained results have been compared with the carbide tool and found that the nano-coated tool produced smoother surfaces than the carbide tool. Also the obtained result have been given as input to Ant Colony Algorithm (ACO) for identifying the optimized cutting parameters which yields better surface finish and improved tool life. The ACO will identify the best spindle speed, feed rate and depth of cut to yield better surface finish with lesser wear rate to increase the tool life.
Keywords |
| TiAlCn, Nano-coating, Ants Colony Algorithm, Turning operation. |
INTRODUCTION |
| Due to revolution in the information and communication technology, NC machines play a vital role in producing higher quality jobs with lesser machining time and reduced cost. Even though, the product lead time and cost increased due to parameters such as tool wear, tool changing time, etc. Thus a necessity arises to improve the tool life to reduce the product lead time and machining cost. This can be achieved by improving the property of the tool material and optimizing the cutting conditions. In this research, the former methodology of improving the cutting tool properties namely high thermal stability, higher wear resistance, higher resistance to thermal shock and impacts, chemically inertness and higher hardness have been achieved by coating the carbide tip with TiAlCn nano particles. Later methodology of optimizing the cutting conditions namely speed, feed and depth of cut have been achieved using Ants Colony Optimization Algorithm. |
| Twenty eight carbide tips have been uniformly coated with the TiAlCn nano particles using CVD technique. These tools have been used in CNC turning machine to machine the mild steel jobs under different cutting conditions. Surface roughnesses of the obtained jobs have recorded to generate a non-linear equation and this equation has been used as the fitness function for the ACO technique to optimize the cutting parameters. Thus the tool life has been improved by enhancing the tool properties and optimizing the cutting conditions and in-turn it reduces the product lead time and cost. The remainder of this paper is organized as follows. The pervious carried out by the researchers have been given in the section 2. The problem description is introduced in Section 3. The detail of proposed algorithm is described in Section 4. In Section 5, the computational experiments are performed on cutting tool problems and the ACO concepts in the section 6 followed by the results and conclusions in Section 7 and 8. |
II. LITERATURE SURVEY |
| In general, the selection of the cutting parameters for machining is based on the experience. In such cases, the experience of the operator plays a major role, but even for a skilled operator it is very difficult to attain the optimum values each time. So various research works have been made in this area. Taylor (1907) conducted different analytical and experimental approaches for the optimization of machining parameters. Gilbert (1950) developed the optimization model for turning operation to maximize the production rate and minimize the cost. Brewer and Rueda (1963) carried out simplified optimum analysis for reducing the machining cost. Armarego and Brown (1969) applied differential calculus for unconstrained machine parameter optimization. Ermer & Kromodiharajo (1981) developed a mathematical model to optimize a constrained multi-pass machining problem. Prasad et al (1997) developed an optimization module for determining process parameters for turning operations as part of generative CAPP system. Wang and Jawahir (2005) optimized the cutting conditions using Genetic Algorithm for Multi-pass turning operations. The authors also optimized with and without tool wear. Wang and Xie (2005) used the concept of ACO for optimizing the process planning in punch and laser cutting machine. ACO used to identify the optimal tool path. Cowton and Wirth (2007) included the cost parameter for optimization of cutting conditions namely speed and tool life. Hamid and Mostafa (2007) proved that the ACO can produce the encouraging results compared to the mathematical models for the plant layout optimization problems. Udomsakdigool and Kachitvichyanukul (2008) found that the ACO finds good solution by exchanging the information among the colonies. Martin Noel et al (2009) described some numerical experiments related to a tool management model for a flexible machine equipped with a tool magazine, variable cutting speed, and sensors to monitor tool wear. |
III. CUTTING TOOL PROBLEM |
| Cutting is the process of removal of materials from the work-piece by moving the cutting tool against the work-piece. Cutting tool problem is the problem of identifying the suitable cutting parameters such as feed rate, speed, depth of cut, etc to produce component with better surface finish. This problem of identifying the suitable parameters simultaneously by satisfying the cutting constraints is called as the cutting tool optimization problem. |
| The major issues in cutting tool optimization problems are the machine tool limitations such as maximum spindle speed, feed rate, maximum power, maximum machining force, etc and the cutting tool parameter conflictions. Let ‘J’ be a set having ‘n’ number of jobs {Jn} to be machined. These ‘Jn’ jobs should be machined such a way by satisfying the constraints like feed rate (f), speed (s), depth of cut per pass (d), tool diameter (D), width of cut (w) and also should produce the jobs with better surface finish (Ra), minimum cutting cost (C), minimum time (t), better tool life (l) and with minimal vibrations (v). |
| Thus a necessity arises to avoid these cutting tool parameter conflictions. Therefore, the parameter values have to be optimized by satisfying the related cutting constraints. Every optimization problem should have an objective function for optimization. Inorder to frame the objective function, sample parameters were taken and the surface roughness values were observed from the machined surface. |
IV. EXPERIMENTAL SETUP |
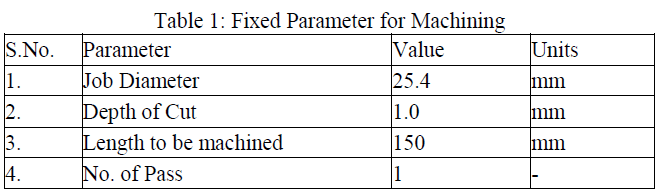
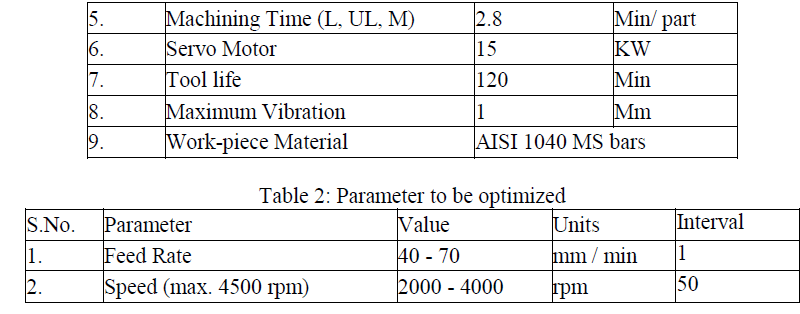
| Six-axis CNC turning machine was taken for the experimentation purpose with single point cutting tool coated with nano NiAlCn particles. Inorder to reduce the complexity of the machining problem, in this research, the machining parameters have been categorized as fixed parameter and the parameter to be optimized. The former is given in the Table 1 and the later given in the Table 2. |
 |
 |
| Even though the modern CNC machine was used in this experimentation, some of the assumptions considered are as follows. |
| Tool and job holder are rigid without any deflection, |
| Heat generated by the cutting will be removed by the coolant (Wet condition), |
| Machine has been performing on the desired feed and speed rate. |
| Single point cutting tool without chip breaker geometry has been used. |
| The cutting inserts were clamped onto a right hand tool holder. |
| Rust layers were removed in order to minimize any effect of in-homogeneity. |
| The main objective is to identify the suitable cutting parameters by satisfying the above mentioned constraints to improve the surface roughness. |
V. SURFACE ROUGHNESS |
| ‘Ra’ is the most commonly used notation to describe the surface roughness of the machined components. It is defines as the integral value of the absolute value of the roughness profile measured over an evaluation length [13] and is given in the Equation 1. |
| Ra = (1 / L) * 0∫L Z(x) dx (1) |
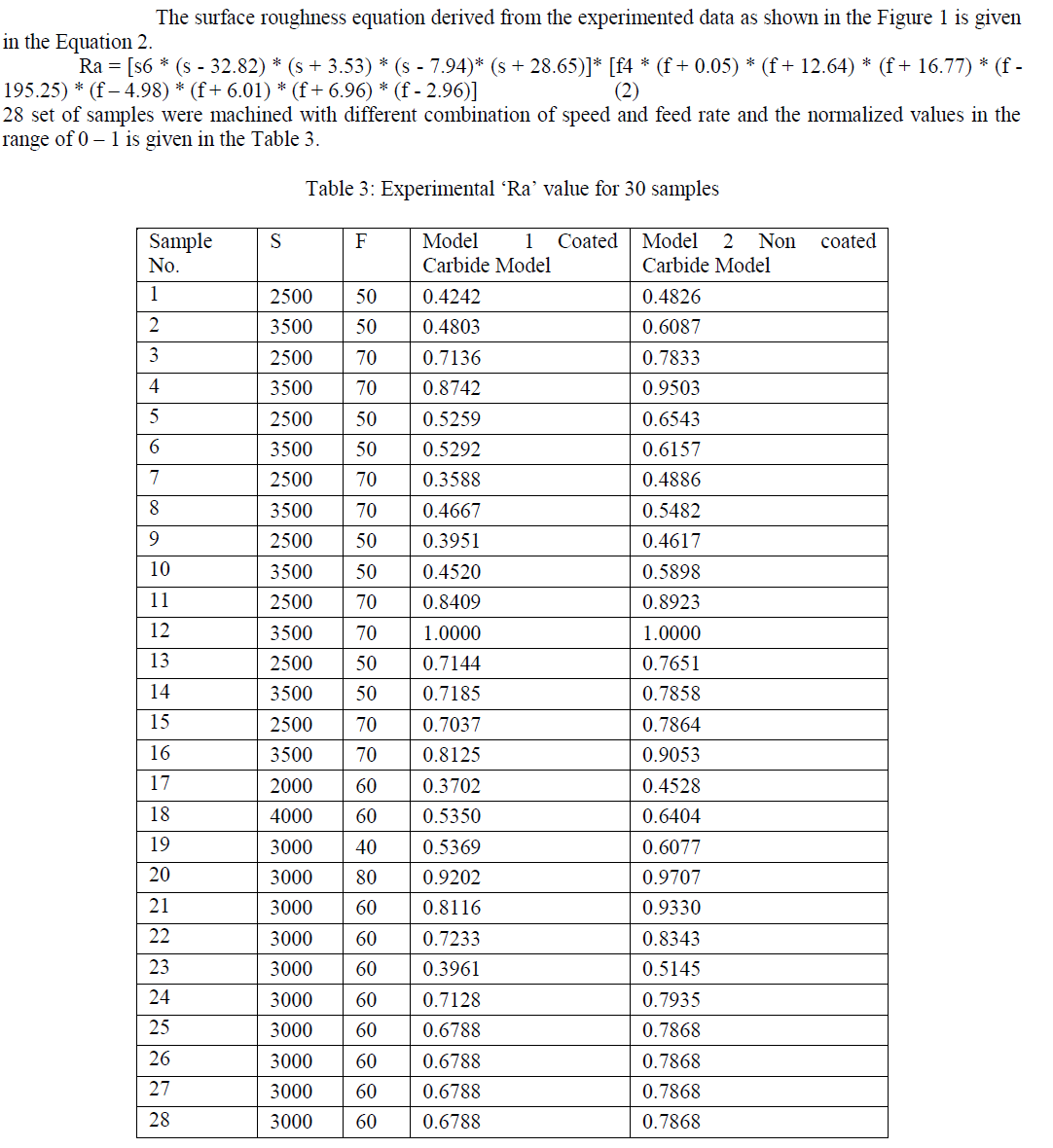
| Whereas, Z(x) is the area of each peak along the length ‘L’ of job that had machined. The average roughness value is the sum of total area of peaks and valleys divided by the evaluation machined length of the job. The average roughness is measured in μm. Then turning operation were performed using nano-coated tool and the standard carbide tool, the obtained results for the various cutting conditions are given in the figure 1. In the Figure 1, X-axis represents the speed and feed rate in rpm and mm/minute respectively. From the Figure 1, it is clear that the surface roughness value obtained using nano-coated tool have produced better results compared to the HSS tool in all the samples. |
 |
 |
| Normally, the manufacturer’s handbook can provide the cutting parameters for different conditions, but the parameters have not been suitable for the coated tools and the properties should be selected based on the static and dynamic characteristic of the coated tool. Inorder to obtain the better surface finish by optimizing the cutting condition is a complex process with multiple constraints, time and cost consuming. So this study uses an intelligent algorithm called Ant Colony Algorithm for optimizing the cutting condition to produce better surface finish products. |
VI. ANT COLONY ALGORITHM |
| Ant colony algorithm is the population based search algorithm derived from the behavior of the ants which selects the nearest path to achieve the target by applying a stochastic local decision policy based on two parameters called trials and attractiveness. So in this research, ACO has been used to optimize the cutting tool problem. A comprehensive review on ant algorithms can be found in Dorigo and Stutzle (2004). |
6.1 Initialize the network |
| Generally, ACO has a finite-size colony of artificial ants allowed to start from the initial node for searching iteratively a good-quality solution using pheromone updation rule to reach the target node. To facilitate the movement of the ants, a network with the parameters namely speed and feed rate are first coded into a network structure with first column having nodes for ants trail, second column having the normalized spindle speed values ranges from 2000 to 4000 rpm with the interval of 100 rpm, third column of nodes with normalized feed rate values ranging from 50 to 70 mm/min with the interval of 2 mm/min and the fourth column is the target node which calculates the surface roughness. The framed ant colony network is shown in the figure 2. |
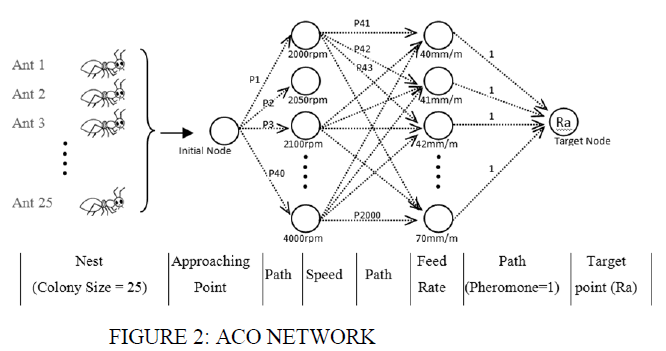 |
| Each node should be linked with each other nodes in the adjacent columns of the network. The link value is called as the pheromone value and the value should be based on the number of ant travel. The number of ants to solve the problem is determined based on the desired accuracy in the solution and as the number of ants increases, proportionally computational time will also increase. |
| 6.2 Initialize the Pheromone Value |
| In cutting tool optimization problem, the parameters namely speed and feed are having different units, so these parameters have been normalized in the range of zero to one to identify the optimized value. For the first trail in each iteration, the pheromone values have been selected from random number generator in the range of 0.001 to 0.1 to prevent the algorithm from prematurely converging to a solution and to avoid the stagnation of the travel in particular path respectively. |
| 6.3 PHEROMONE UPDATING RULE |
| As the number of ants passed the path, the pheromone value increases and indicates that is the shortest path for the remaining ants moving behind it. When the path violates the constraints, the pheromone value gets decreased and indicates the other ants not to move further in that path. Furthermore, this chemical trail (pheromone) has a decreasing action over time because of evaporation of pheromone, to avoid the global stagnation. In this research, the ants are divided into five sub-colony of equal size five and each group uses different heuristic information to guide their search, thereby the search space increases and also the stagnation condition avoided. Figure 3 presents a decision-making process of ants choosing their trips. |
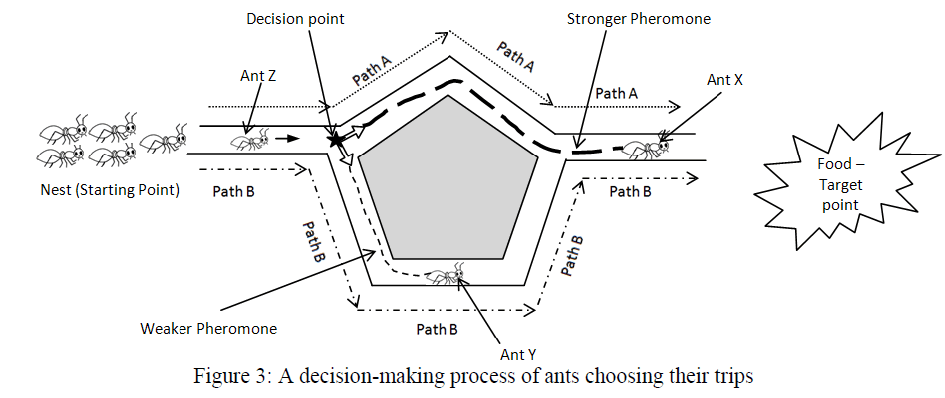 |
| From Figure 3, for the ants, there are two paths namely ‘path A’ and ‘path B’ to reach the target point. Former is the shortest path and the later is the longest path. When ants meet at their decision-making point, some ant may choose path A and some other ant may choose path B randomly. Assume these ants are crawling at the same speed, those ants choosing short side (path A) arrive at target point B more quickly than those choosing long side (path B). The ants choosing by chance the short side are the first to reach the nest. The short side receives more pheromone than the long one. Thus this process increases the probability for further ants to select the short path (path A) rather than the long one (Path B). The thickness of broken line in Figure 3 is direct ratio to the number of ant approximately. In ACO, the pheromone value of the path/link has to be updated based on the number of ant passage i.e. based on the objective function value and the pheromone is calculated using the Equation 3. |
| τij (t+1) = Δτij + (1- ρ) τij (t) Eq. 3 |
| Whereas, ‘ρ’ denotes the evaporation rate of the pheromone and is set as 0.01 in this work based on the sensitivity analysis result. ‘τ’ and ‘t’ represent the pheromone value of the path and trails respectively. ‘Δτ‘ represents the proportional change in the surface roughness value for the cutting parameters selected in the ‘t+1’ trial. ‘i' and ‘j’ represent the speed node and feed node selected by the ant. Thus the pheromone value of the link connecting the speed node ‘i' with ‘feed node ‘j’ has been updated to new value. These values only help the forthcoming ants to take decision using ants moving rule. |
| 6.4 Ants moving rule |
| Ants moving rule help the ants to travel from the nest to the target point in shortest route. The two condition of ant moving rule are as follows. |
| (1) For initial iteration, Ants can select any of the random paths. |
| (2) For remaining iterations, the probability of the kth ant choosing the path is given by Equation 4. |
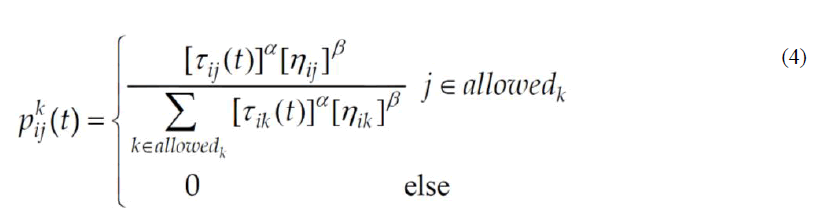 |
| Whereas ‘α’ and ‘β’ are important parameters which determine the relative influence of the trail pheromone and the heuristic information. Based on the number of ant passage, the pheromone has to be updated using updating rules. |
| 6.5 Global Updating rule |
| In ACO, only the best ant updates the pheromone trails and that the value of the pheromone is bound. Therefore, the pheromone updating rule is given by Equation 5. |
| τij (t +1) = τmin∫τmax {Δ τij (best) + (1- ρ) τij (t)} (5) |
| where as τmax and τmin are respectively the upper and lower bounds imposed on the pheromone and Δbest belongs to the best tour which yields better surface finish. |
6.6 OBJECTIVE FUNCTION |
| The main objective of this research is to determine the parameters namely speed and feed rate to produce components with better surface finish in turning operation and is given in the Equation 2. After applying ACO operators, the best valued path should be stored separately in the database. This completes a iteration of ACO algorithm. Such iterations are continued till the termination criterion achieved and the best from the each iteration should be stored in the database separately. |
6.7 Stopping rule |
| There are many conditions for ants to stop their travelling, in this research termination conditions are maximum number of iterations has been set to 200 and continuous 5 iterations produces same result. Finally all the best values are used to construct the global ACO network and same procedure repeated to identify the global best value. |
VII. RESULT |
| The developed ACO were tested with the standard benchmark problems and the obtained results were found satisfactory. The ACO output will give the better optimized speed and feed rate as 2500 rpm and 40 feed rates give the better surface finish of 124. Thus it become clear that the value obtained is matching the benchmark problem dataset. The time taken for achieving the result is little bit lesser compared to the other algorithms, as the ACO searching less the time and is based on the parameters α, β and ρ. |
VIII. CONCLUSIONS |
| In this research, NiAlCn coated tool was used to machine the components at various speed and feed rates in the desirable range. The corresponding surface roughness value also calculated and tabulated. Based on the tabulated values, surface roughness equation has been derived and has been considered as the fitness function in ACO to decide the best possible combination of speed and feed rate by satisfying the cutting constraints to obtain better surface finish. The result of experiment has shown that the proposed ACO algorithm is a precise method for cutting tool problems. The optimized cutting parameter from ACO will lead to reduced cutting time, cutting force and produce better surface finish under certain conditions with minimal errors. |
IX. SCOPE OF FUTURE WORK |
| By conducting various experiments it was found that the parameters like depth of cut, length of cut, tool nose radius and job diameter also plays role in the cutting process optimization, but these parameters were assumed to be constant in this research work. So these parameters need to be considered for the perfect optimization. |
References |
|