Adaptive K-Means Clustering Techniques
For Data Clustering

Manjinder Kaur; Navjot Kaur; Harkamaldeep Singh

Adaptive K-Means Clustering Techniques For Data Clustering

Manjinder Kaur¹, Navjot Kaur², Harkamaldeep Singh³

Student, M.tech in Department of Electronics and Communication Engineering, IET, Bhaddal, Ropar,India
Assistant Professor, Department of Electronics and Communication Engineering, IET, Bhaddal, Ropar,India
Assistant Professor, Department of Electrical and Electronics Engineering, IET, Bhaddal, Ropar,India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

In the presented work, a modified k-means clustering is proposed. It adapts itself according to the image based on color based clustering. The no. of clusters using the color features are computed based on histogram analysis in gray format. The peak of the histogram is the main source of computation of no. of colors in the image and based on the same, the image data are clustered.

Keywords

K-means clustering, segmentation

INTRODUCTION

K-Means is a rather simple but well known algorithm for grouping objects, clustering. Again all objects need to be represented as a set of numerical features. In addition the user has to specify the number of groups (referred to as k) he wishes to identify. Each object can be thought of as being represented by some feature vector in an n dimensional space, n being the number of all features used to describe the objects to cluster. The algorithm then randomly chooses k points in that vector space, these points serve as the initial centres of the clusters. Afterwards all objects are each assigned to the centre they are closest to. Usually the distance measure is chosen by the user and determined by the learning task. After that, for each cluster a new centre is computed by averaging the feature vectors of all objects assigned to it. The process of assigning objects and recomputing centres is repeated until the process converges. The algorithm can be proven to converge after a finite number of iterations. Several tweaks concerning distance measure, initial centre choice and computation of new average centres have been explored, as well as the estimation of the number of clusters k. Yet the main principle always remains the same. k-means clustering is a method of vector quantization, originally from signal processing, that is popular for cluster analysis in data mining. k-means clustering aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean, serving as a prototype of the cluster. In the conventional k-mean algorithm, the number of elements in each cluster is stochastic. It is possible that some groups own a large proportion of elements while others just possess a few of them. However, in some situations, the proportion of elements in each cluster need to be controlled so as to make the distribution of elements satisfied. Paper is organized as follows. Section II describes automatic text detection using morphological operations, connected component analysis and set of selection or rejection criteria. The flow diagram represents the step of the algorithm. After detection of text, how text region is filled using an Inpainting technique that is given in Section III. Section IV presents experimental results showing results of images tested. Finally, Section V presents conclusion.

II. RELATED WORK

DongjuLiu and JianYu [1] proposed that Otsu method is one of the most successful methods for image thresholding. This proves that the objective function of Otsu method is equivalent to that of K means method in multilevel thresholding. These both are based on a same criterion that minimizes the within-class variance. However, Otsu method is an exhaustive algorithm of searching the global optimal threshold, while K-means is a local optimal method. Moreover, K-means does not require computing a gray-level histogram before running, but Otsu method needs to compute a gray-level histogram firstly. Aimi Salihah Abdul-Nasir, Mohd Yusoff Mashor and Zeehaida Mohamed [2] presented that Malaria is a serious global health problem that is responsible for nearly one million deaths each year. With the large number of cases diagnosed over the year, rapid detection and accurate diagnosis of malaria infection which facilitates prompt treatment are essential to control malaria. This presents a color image segmentation approach for detection of malaria parasites that has been applied on malaria images of P. vivax species. In order to obtain the segmented red blood cells infected with malaria parasites, the images are first enhanced by using partial contrast stretching. Then, an unsupervised segmentation technique namely k-means clustering has been used to segment the infected cell from the background. Juanying Xie, Shuai Jiang [3] has studied K-means clustering is a popular clustering algorithm based on the partition of data. However, there are some shortcomings of it, such as its requiring a user to give out the number of clusters at first, and its sensitiveness to initial conditions, and its easily getting to the trap of a local solution etc. The global K-means algorithm proposed by Likas et al is an incremental approach to clustering that dynamically adds one cluster center at a time through a deterministic global search procedure consisting of N (with N being the size of the data set) runs of the K-means algorithm from suitable initial positions. Juntao Wang and Xiaolong Su [4] presents that the K-Means clustering algorithm is proposed by Mac Queen in 1967 which is a partition-based cluster analysis method. It is used widely in cluster analysis for that the K-means algorithm has higher efficiency and scalability and converges fast when dealing with large data sets. However it also has many deficiencies: the number of clusters K needs to be initialized, the initial cluster centers are arbitrarily selected, and the algorithm is influenced by the noise points. In view of the shortcomings of the traditional K-Means clustering algorithm, here presents an improved K-means algorithm using noise data filter. Hongjun Wang, Jianhuai Qi,Weifan Zheng and Mingwen Wang[5] studied that K-means is the most popular clustering algorithm and many researchers pay much attention to improving it. In this paper the authors find that some features influence so much on the results of clustering. For improving the K-means algorithm, the authors design a novel balance K-means algorithm. The main idea is that we normalize all the feature values of dataset before clustering. So all the features play the same important role in the clustering, which make the k-means balanced. Pritesh Vora and Bhavesh Oza [6] has presented that In Data Mining, Clustering is an important research topic and wide range of unsupervised classification application. Clustering is technique which divides a data into meaningful groups. K-mean is one of the popular clustering algorithms. K-mean clustering is widely used to minimize squared distance between features values of two points reside in the same cluster . Mushfeq-Us-Saleheen Shameem and Raihana Ferdous [7] Studied that Document Clustering is a widely studied problem in Text Categorization. It is the process of partitioning or grouping a given set of documents into disjoint clusters where documents in the same cluster are similar. K-means, one of the simplest unsupervised learning algorithms, solves the well known clustering problem following a simple and easy way to classify a given data set through a certain number of clusters (assume k clusters) fixed a priori. Tayfun Dogdas and Selim Akyokus [8] presented that Here using expectation-maximization clustering algorithm and a simple multidimensional projection method for visualization and data reduction. The multidimensional data is projected into a 2D Cartesian coordinate system. We run EM and K-Means algorithms on the transformed data. The system uses Microsoft Spatial Data Base Engine as a GIS tool for visualization. Here used Expectation. Faliu Yi and Inkyu Moon [9] proposed that In the conventional K-means algorithm, the input data are automatically grouped into corresponding cluster by minimizing the within-cluster sum of squares. However, the traditional K-means algorithm doesn’t do any constraints to the number of elements in each group. In the area of logistics management, each cluster will need to satisfy with a predefined number of elements. S Gnanapriya and P Shiva Ranjani [10] studied that Clustering is a machine learning technique that places data elements into related groups. Clustering can be defined as a process of organizing objects into groups whose members are similar in some way. The primary goal of clustering is to determine the intrinsic grouping in a set of unlabeled data. K-Means (KM) is one of the widely used algorithms in clustering techniques. KM is the simplest unsupervised learning algorithms that can solve the well-known clustering problem. Raed T. Aldahdooh Wesam Ashour [11] presented that Partition-based clustering technique is one of several clustering techniques that attempt to directly decompose the dataset into a set of disjoint clusters. K-means algorithm dependence on partitionbased clustering technique is popular and widely used and applied to a variety of domains. K-means clustering results are extremely sensitive to the initial centroid; this is one of the major drawbacks of k-means algorithm. Soumi Ghosh and Sanjay Kumar Dubey [12] proposed that in the arena of software, data mining technology has been considered as useful means for identifying patterns and trends of large volume of data. This approach is basically used to extract the unknown pattern from the large set of data for business as well as real time applications. It is a computational intelligence discipline which has emerged as a valuable tool for data analysis, new knowledge discovery and autonomous decision making. The raw, unlabeled data from the large volume of dataset can be classified initially in an unsupervised fashion by using cluster analysis i.e. clustering the assignment of a set of observations into clusters so that observations in the same cluster may be in some sense be treated as similar. Amir Ahmad and Lipika Dey [13] has studied that use of traditional k-mean type algorithm is limited to numeric data. This presents a clustering algorithm based on k-mean paradigm that works well for data with mixed numeric and categorical features. Here propose new cost function and distance measure based on co-occurrence of values. The measures also take into account the significance of an attribute towards the clustering process. Nivan Ferreira, James T. Klosowsk, Carlos E. Scheidegger and Cláudio T. Silva[14] presented that Scientists study trajectory data to understand trends in movement patterns, such as human mobility for traffic analysis and urban planning. This introduce a novel trajectory clustering technique whose central idea is to use vector fields to induce a notion of similarity between trajectories, letting the vector fields themselves define and represent each cluster. Here present an efficient algorithm to find a locally optimal clustering of trajectories into vector fields, and demonstrate how vector-field k-means can find patterns missed by previous methods. T Hitendra Sarma, P Viswanath and B Eswara Reddy [15] proposed that In unsupervised classification, kernel k-means clustering method has been shown to perform better than conventional k-means clustering method in identifying nonisotropic clusters in a data set. The space and time requirements of this method are O(n2), where n is the data set size. Because of this quadratic time complexity, the kernel k-means method is not applicable to work with large data sets. Here proposes a simple and faster version of the kernel k-means clustering method, called single pass kernel k-means clustering method.

III. ALGORITHM

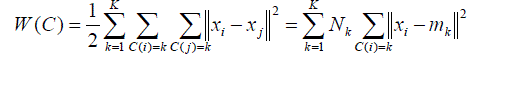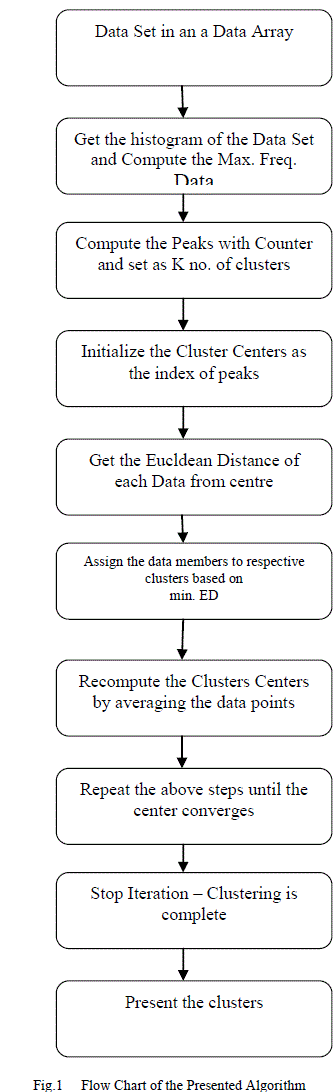IV.RESULTS

IV. CONCLUSION

K-means converges, but it finds a local minimum of the cost function. It Works only for numerical observations (for categorical and mixture observations, K-means is a clustering method). Fine tuning is required when applied for image segmentation; mostly because there is no imposed spatial coherency in k-means algorithm Often works as a starting point for sophisticated image segmentation algorithms.

References

Aimi Salihah Abdul-Nasir1, Mohd Yusoff Mashor2, Zeehaida Mohamed3, “ Colour Image Segmentation Approach for Detection of Malaria Parasites Using Various Colour Models and k-Means Clustering”, Issue 1, Volume 10, January 2013
Juanying Xie, Shuai Jiang, “A simple and fast algorithm for global K-means clustering”, 978-0-7695-3987-4/10 $26.00 © 2010 IEEE.
Pritesh Vora, Bhavesh Oza, “A Survey on K-mean Clustering and Particle Swarm Optimization”,International Journal of Science and Modern Engineering, Vol. 1, Issue- 3, Februry 2013.
Mushfeq-Us-Saleheen Shameem, Raihana Ferdous, “An efficient K-Means Algorithm integrated with Jaccard Distance Measure for Document Clustering” 978-1-4244-4570-7/09/$25.00 ©2009 IEEE .
Tayfun Dogdas, Selim akyokus, “ Document clustering using GIS visualizing and EM clustering method” 978-1-4799-0661-1/13/$31.00 ©2013 IEEE.
S Gnanapriya1 and P Shiva Ranjani1 , “ Initialization K- Mean using Ant colony Optimization”, International Journal of Engineering Research science and Technology, Vol. 2, No. 2, May 2013.
Raed T. Aldahdooh Wesam Ashour, “ DIMK-means―Distance-based Initialization Method for K-means Clustering Algorithm” I.J. Intelligent Systems and Applications, 2013, 02, 41-51.
Soumi Ghosh, Sanjay Kumar Dubey, “ Comparative Analysis of K-Means and Fuzzy C- Means Algorithms” (IJACSA) International Journal of Advanced Computer Science and Applications, Vol. 4, No.4, 2013.
Amir Ahmad, Lipika Dey, “A k-mean clustering algorithm for mixed numeric and categorical data”, Data and Knowledge Engineering 63 (2007) 503-527.
Nivan Ferreira1, James T. Klosowski2, Carlos E. Scheidegger2, Cláudio T. Silva1, “Vector Field k-Means: Clustering Trajectories by Fitting Multiple Vector Fields”, Vol. 32 (2013) No. 3.
T Hitendra Sarma1, P Viswanath2 and B Eswara Reddy3, “ Single pass kernel k-means clustering method” Sadhana Vol. 38, Part 3, June 2013, pp. 407–419._c Indian Academy of Sciences.