ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| M. A. Hoque1, M. S. Hossain2, M. Shahabuddin3 Lecturer in Mathematics, Department of Arts and Sciences, Ahsanullah university of Science and Technology, Dhaka-1208, Bangladesh1 Assistant Professor of Mathematics, Department of Arts and Sciences, Ahsanullah university of Science and Technology, Dhaka-1208, Bangladesh2 Professor of Mathematics, Department of Arts and Sciences, Ahsanullah university of Science and Technology, Dhaka-1208, Bangladesh3 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The homogeneous and isotropic cosmological models in Brans-Dicke theory have been discussed. Besides the cosmological term L(x ) to the Brans-Dicke Lagrangian using Robertson-Walker line element and energy tensor of a perfect fluid were also examined for the mass expansion of the universe. After correcting an error in their work, we also tried to extend our results by calculating cosmological term using Berman and Som [1] solution and showed the results obtained from the application of theory also satisfy uniform cosmological model.
Keywords |
| Cosmological Constant, Uniform Cosmological model, Modified Brans-Dicke Lagrangian, Cosmology |
INTRODUCTION |
| It is well-known that Einstein originally introduced the cosmological constant in order to obtain a static model of the universe. Because the large scale recession of the galaxies i.e, the expansion of the universe had not been discovered at the time. This was discovered later by Hubble in twenties and thirties. After introducing cosmological constant by Einstein, its real significance was studied by various cosmologies [2] but no satisfactory results of its meaning have yet been reported. Zel’dovich [3] has tried to visualize the meaning from the theory of elementary particles because the constant corresponds to the vacuum energy. However, to obtain the static model of the universe, Einstein might have been able to predict the expansion of the universe or the universe is in a dynamic state ( sec Islam[4]), second edition,2002). |
| Actually Linde [5] has argued the cosmological term arises from spontaneous synnetry breaking and suggested that the term is not a constant but a function of temperature. In cosmology the term may be understood by incorporation with Mach’s [ 6] principle, which suggest the acceptance of Bran’s-Dicke Lagrangian as a realistic case [7,8] and stimulates us to study the term with a modified Brans-Dicke Lagrangian from cosmology and elementary particle physics. Besides, Azad and Islam [9] also studied cosmological constant in the Bianchi type-1 modified Bran’s-Dicke cosmology. After that, Pradhan et.al [10] studied FRW universe with variable G and L terms. A new class of exact solutions of Einstein’s field equations with a perfect fluid source, variable gravitational couple G and cosmological term L for FRW space time is obtained by considering variable deceleration parameter models for the universe. The nature of the variables G(t ), L(t ) and the energy density r (t ) have been examined for the three cases: (i) exponential, (ii) polynomial, and (iii) sinusoidal form. The special types of models for dust, Zel’dovich and radiating universe are also discussed in the light of recent supernovae Ia observations. |
| Besides Endo and Fukui [11] touched upon the Dirac large number hypothesis to obtain uniform cosmological model and which also affect in elementary particle physics. To the best knowledge of the authors no attention has been paid to calculate cosmological term from Brans- Dicke cosmological model of uniform cosmology. This is seen that this cosmological term calculation also satisfies the results of uniform cosmological term. |
| The cosmological term has been assumed as an explicit function of a scalar fieldx , proposed by Bergmann and Wagoner [12], and start with the usual variational principle of general relativity using a Brans-Dicke Lagrangian modified by L(x ): |
 |
| Where R and m L are the scalar curvature and the lagrangian density of matter, which is assumed not to depend explicitly on derivatives of ij g and x plays a role analogous to G-1 . The field equation for the metric field is, then we have, |
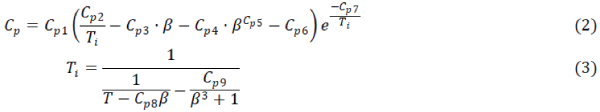 |
| Where, |
 |
| It is also the energy-momentum tensor of matter. Contraction of equation (2) results in |
 |
| While the field equation for x is obtained by varying x and i, x in equation (1) |
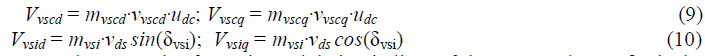 |
| By eliminating R from equations (3) and (4), |
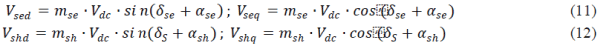 |
| Although Brans-Dicke cosmology does not pay any attention toL , the relation between the matter field and the scalar field can be obtained analytically through an equation analogous to equation (5), besides a certain degree of arbitrariness inevitably accompanies the introduction of a scalar field. Here we assume the simplest case of the coupling of the two fields as follows: |
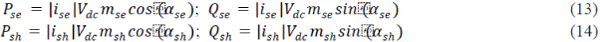 |
| Here the constant m shows how much our theory including L(x ) deviates from that of Brans and Dicke . Then a particular solution of equation (5) is given as |
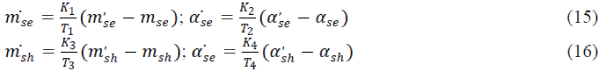 |
| Since we assume L is a function of onlyx , we have |
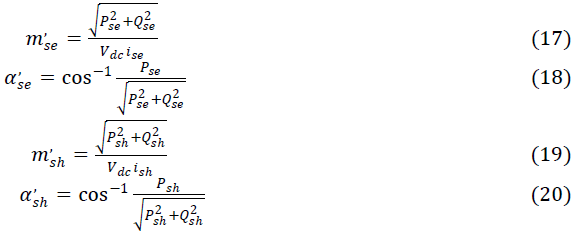 |
| By multiplying equation (2.2) by x and taking the contravariant derivative, we find |
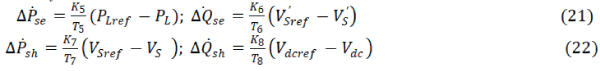 |
Equation (4) then ensures that the conversion law 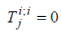 holds. holds. |
III. CALCULATION OF COSMOLOGICAL CONSTANT OF UNIFORM COSMOLOGICAL MODEL |
| For the homogeneous and isotropic universe, applying those equations, the metric is that given by Robertson and Walker, and the energy- momentum tensor, that of a particle fluid, |
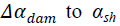 |
| Here a(t ) is the spatial scale factor, k the dimensionless curvature index, e and p the total energy density and pressure of the universe, respectively, and ui a velocity four vector that has components of (1, 0, 0, 0) in the commoving co-ordinates. The (0,0) component of equation (2) is |
 |
| Where x depends only on universal time t and a dot indicates differentiation with respect to t. From equation (6), we obtain |
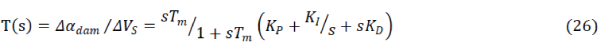 |
| From equation (7), we obtain the variable L as follows: |
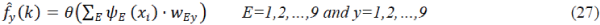 |
| The equation of state in the radiation field 3p =e leads to the vanishing cosmological term. Equation (11) yields the expression for f (x ) as |
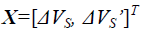 |
The conservation law ; 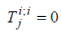 requires the well-known relation requires the well-known relation |
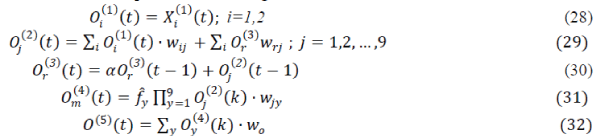 |
| As an example, we consider the case of the matter field where L is not zero. In this field we can neglect pressure, which has less significance for the model of the universe [13]. Then equation (13) gives |
 |
| Here, subscript 0 indicates the present value of a quantity. From equation (10), we obtain the following relation for the big-bang universe: |
 |
Where 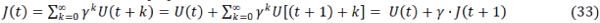 |
| From the equation (11), we have |
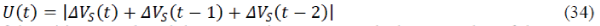 |
| This implies that the cosmological term participates in the mass of the universe, and that may have a significance in determining the mass of an elementary particle when applied to the hadron era as studied in [14]. From equator (12), f (x ) is proportional to a-3 : |
 |
Where  |
| Substituting equations (15) - (17) in to equation (9), we obtain |
 |
| Since in particle physics, the terms of x n are introduced to explain the origin of the mass of an elementary particle by symmetry breaking [15] , we assume the functional form of f (x ) as follows: |
 |
| Substituting equation (19) in to equation (18), we solve in the case of k = 0 , i.e., the flat universe. When we notice two conditions, an expanding universe and an increasing function x (t ), n = 1 which gives the constant cosmological term is not suitable. Then, with n ¹ 1and the assumption of x = 0 at t = 0 , the solution is |
 |
| Equation (17) with equation (20) results in the following relation: |
 |
| By using two conditions, the domain of n arrows is to n < 0. Since equations (20) and (21) satisfy equation (15), |
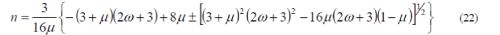 |
| From equation (16) |
 |
| Following Brans and Dicke [7] and Weinberg [16], the gravitational “constant” G is given by the weak field approximation as follows: |
 |
| Equation (24), (20), and (21) present the relation of G with the Hubble constant |
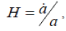 as as |
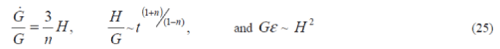 |
| When we put n = -1 in equation (21) and (25), the following relation is obtained: |
 |
| and this is the case of Dirac [17]2 although the cosmological term is not zero but is |
 |
While if we putm = 1, all the equations we obtained reduce to those we obtained reduce to those of Brans and Dicke and equations (22),(23), and (25) give 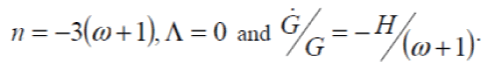 |
| From Berman and Som follows that |
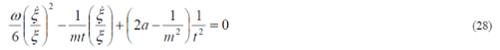 |
| And the solution of the above equation for m is given by |
| m5 - 8m4 - 2m3+54m2 - 24m - 24 = 0 |
| And then listed the following five different solutions in terms of m and the coupling constant w : |
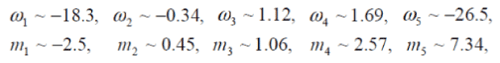 |
| If we put w = -18.3 and t = 1, 2, 3, 4, …….then we have |
| Cosmological constant, L = -14.47, -3.62, -1.61, -0.90, -0.57, -0.40, ……….. |
| This means that, for increasing time cosmological constant is also increasing for Brans-Dicke Cosmology, which also satisfy the uniform cosmological model theory. |
| When the value of w is increasing for the time expansion, i.e. when w = -0.34 and t = 1, 2, 3, 4,…… then we have, |
| Cosmological constant, L = -0.83, -0.209, -0.09, -0.05, -0.03,……. |
| This also means that, for increasing time, cosmological constant is more increasing, which also satisfy the mass expansion of the universe. |
| In similar way, when we use the values of w for the expansion of time i.e w = 1.12, 1.69 and t = 1, 2, 3, 4,………..then we also have, |
| Cosmological constant, L = 1.48, 0.37, 0.16, 0.09, 0.05, …................ |
| And Cosmological constant, L = 1.96, 0.49, 0.22, 0.12, 0.07,……………. |
| This also means that, for increasing time and also for the values of w , that is solved from Bermann and Som Solution, cosmological constant is more and more increasing, which also satisfy expanding of the universe, i.e uniform cosmological theory of Barns-Dicke cosmology. |
IV.DISCUSSION AND CONCLUDING REMARKS |
| The uniform cosmological model using modified Bran’s-Dicke Lagrangian through which cosmological term has been studied from the point of view of cosmology and elementary particle physics and login is partially clarified. The error in the paper of Endo and Fukui has been corrected and we have solved uniform cosmological model for cosmological constant using Bransdicke Cosmology and calculated their results applying the numerical values of t &w which are also satisfy the theory of uniform cosmological model in Brans-Dicke cosmology and elementary particle physics might give a clue to solve the problems in large number hypothesis and Mach’s principles. |
ACKNOWLEDGMENT |
| We are very grateful to Professor Dr. A. K. Azad for constants encouragement and critical reading of the manuscript. We also express our sincere thanks to Ahsanullah University of Science and Technology, Dhaka, Bangladesh for giving the computing facility. |
References |
|