An approximation method for the solving a
class of nonlinear integral equations

Mahmood Saeedi Kelishami

An approximation method for the solving a class of nonlinear integral equations

Mahmood Saeedi Kelishami
Associate Professor, Department of Applied mathematics, Islamic Azad University Rasht Branch, Rasht, Iran

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

A Chebyshev collocation method has been presented to solve nonlinear integral equations in terms of Chebyshev polynomials. This method transforms the integral equation to a matrix equation which corresponds to a system of nonlinear algebraic equations with unknown Chebyshev coefficients. Finally, some examples are presented to illustrate the method and results discussed.

Keywords

Chebyshev collocation method; Fredholm–Volterra integral equations; Nonlinear integral equation

INTRODUCTION

As we know the Chebyshev polynomials are one of the best orthogonal polynomials that have important role particularly in numerical analysis. AChebyshev-matrix method for solving nonlinear integral equations have been presented by Sezer and Doğan [15]. In this study, Chebyshev collocation method, which is given by Akyüz and Sezer [3], is developed for nonlinear integral equation.

Fredholm nonlinear integral equation of the second kind and first kind are given by

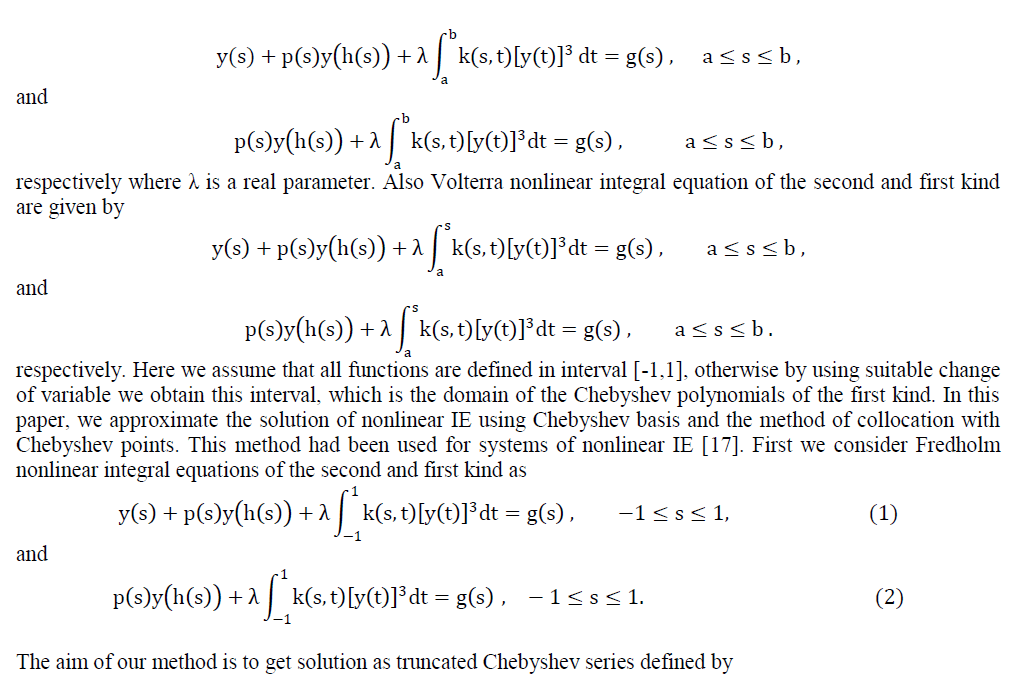FUNDAMENTAL RELATIONS

We suppose that kernel functions and solutions of equations (1) and (2) can be expressed as a truncated Chebyshev series. Then (3) can be written in the matrix form

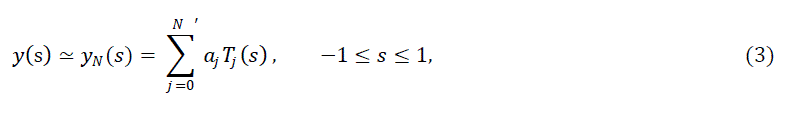THE METHOD FOR SOLUTION OF NONLINEAR FREDHOLM INTEGRAL EQUATIONS

In this section, we consider Fredholm equation in (1) and approximate to solution by means of finite Chebyshev series defined in (3). The aim is to find Chebyshev coefficients, that is, the matrix A in the matrix form (4). We use (4), (5) and (9) for Si in (6) to get

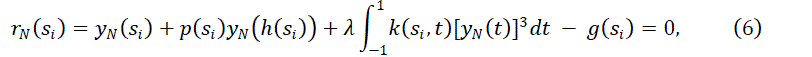THE METHOD FOR SOLUTION OF NONLINEAR VOLTERRA INTEGRAL EQUATIONS

We now consider the nonlinear Volterra integral equations of the second and first kind as

ILLUSTRATIONS

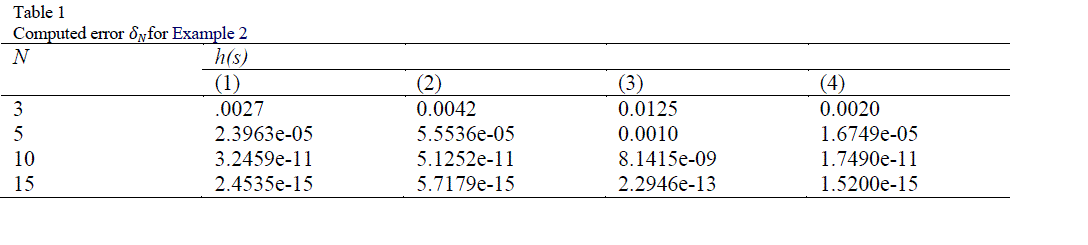
In this section, we consider threeexamples. All results were computed using MATLAB.

Example 1. Let us first consider the nonlinear Volterraintegral equation of second kind

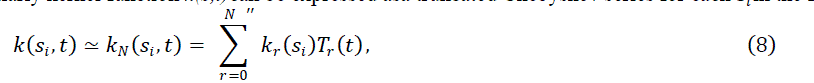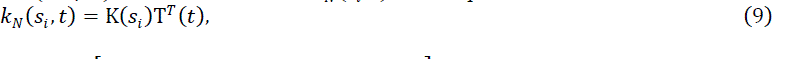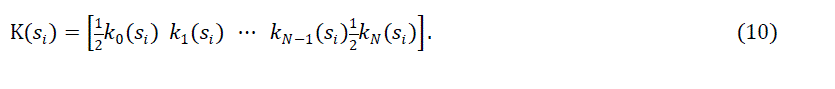CONCLUSIONS

Here, we use the Chebyshev collocation method to solve nonlinear integral equation of the first and second kind Fredholm–Volterra integral equations of the second kind by transformingour problems into a system of nonlinear algebraic equations. With using Chebyshev collocations points,the unknown vector is Chebyshev expansion coefficients of the solution. Numerical examples show the accuracyof this method.

References

A. Akyüz, H. CerdikYaslan, An approximation method for the solution of nonlinear integral equations, J. Appl. Math. Comput. 174 (2006) 619-629.
A. Akyüz-Daciolu, Chebyshev polynomial solutions of systems of linear integral equations, Appl. Math. Comput. 151 (2004) 221– 232.
A. Akyüz, M. Sezer, A Chebyshev collocation method for the solution linear integro differential equations, J. Comput. Math., 72 (1999) 491-507.
A. Avudainayagam, C. Vani, Wavelet-Galerkin method for integro-differential equations, Applied Numerical Mathematics, 32 (2000), 247-254.
B. Sepehrian, M. Razzaghi, Single-term Walsh series method for the Volterraintegro-differential equations, Engineering Analysis with Boundary Elements, 28 (2004) 1315-1319.
E. Babolian, F. Fattahzadeh, E. GolparRaboky, A Chebyshev approximation for solving nonlinear integral equations of Hammerstein type , J. Appl. Math. Comput. 189 ( 2007 ) 641-646.
E. Babolian, F. Fattahzadeh, Numerical computation method in solving integral equations by using Chebyshev wavelet operational matrix of integration , J. Appl. Math. Comput. 188 ( 2007 ) 1016-1022.
E. Babolian, F. Fattahzadeh, Numerical solution of differential equations by using Chebyshev wavelet operational matrix of integration, J. Appl. Math. Comput. 188 ( 2007 ) 417-426.
E. Babolian, S. Abbasbandy, F. Fattahzadeh, A numerical method for solving a class of functional and two dimensional integral equations, J. Appl. Math. Comput. 198 (2008) 35–43.
H. Adibi, P. Assari ,Chebyshev Wavelet Method for Numerical Solution of Fredholm Integral Equations of the First Kind, J. Math. Problems in Engineering , vol. 2010, pp. 1-18, 2010.
K. Maleknejad, Y. Mahmoudi, Taylor polynomial solution of high-order nonlinear Volterra-Fredholmintegro-differential equations, Appl. Math. Comput., 145 (2003) 641-653.
L. Fox, I.B. Parker, Chebyshev Polynomials in Numerical Analysis, Oxford University Press, London, 1968.
L.M. Delves, J.L. Mohamed, Computational Methods for Integral Equations, Cambridge University Press, Cambridge, 1985.
M. Sezer, M. Kaynak, Chebyshev polynomial solutions of linear differential equations, Int. Math. Educ. Sci. Technol., 27 (1996), 607- 61.
M. Sezer, S. Doğan, Chebyshev series solution of Fredholm Integral equations, Int. J. Math. Educ. Sci. Technol., 27 (1996) 649-657.
M.T. Rashed, Numerical solutions of functional integral equations, Appl. Math. Comput. 156 (2004) 507–512.
T.W. Sag, Chebyshev iteration methods for integral equations of the second kind, Math. Comput. 24 (110) (1970) 341–355.