International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

ANALYSIS OF ACCELERATED LIFE TESTING USING GEOMETRIC PROCESS FOR FRECHET DISTRIBUTION

Sana Shahab1 and Ariful Islam2
  1. Research Scholar, Department of Statistics & Operations Research, Aligarh Muslim University, Aligarh, Uttar Pradesh, India
  2. Professor, Department of Statistics & Operations Research, Aligarh Muslim University, Aligarh, Uttar Pradesh, India

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

In Accelerated life testing (ALT), a log-linear relationship between life and stress is used. However instead of original parameters, transformed parameters are used for estimation which loose originality due to various assumptions. In this paper the geometric process is used for the analysis of ALT under constant stress for the Frechet Distribution. The maximum likelihood procedure is followed to estimate the parameters of the model and also evaluate the performance of confidence intervals through simulation

Keywords
Maximum Likelihood Estimation; Reliability Function; Fisher Information Matrix; Asymptotic Confidence Interval; Simulation.

INTRODUCTION
Accelerated life testing (ALT) is the most common way to assess a product’s life and gives desired information on its life under normal use. It is widely used in industry for improving the performance of products. It allows the experimenter to apply more severe stresses on the parameters of lifetime distributions to obtain information quickly than would be possible under normal operating conditions. Under such test settings, products are tested at higher-than usual levels of stress to induce early failure as operating in normal conditions require large number of units and hence more time is consumed which is not feasible. The goal of accelerated life analysis is to utilize the test data to extrapolate a product’s life distribution and its associated parameters at a normal stress level. Such a test saves time and expenses compared to tests at normal conditions.
The most difficult task in Accelerated life testing is to choose what stress is to be applied and in what manner. There are various types of Stress loading in ALT which includes constant, cyclic, step, progressive and random stress. Failure data obtained from ALT can be divided into two categories: complete (all failure data are available) or censored (some failure data are missing).
Many methodologies have been developed related to accelerated life testing and are widely used in industry. See Yurkowski, Schafer and Finkelstein[1], Nelson[2], Meeker[3], Viertl[4]. Lawless[5], Cox and Oakes[6], Lipson and Sheth[7], Viertl[4] have recent book chapters on ALT methodologies.
In the current study, we discuss the application of constant stress in accelerated life testing. Constant-stress ALT for two parameter Birnbaum-Saunders (BS) distribution is introduced by Owen[8]. Reliability bounds and critical time for the Birnbaum-Saunders distribution, see Chang[9], Dupuis and Mills[10], Xu and Tang[11,12]. Work based on censored data includes Rieck[13], Jeng[14], Ng et al. M[15] and Wang et al[16] . Yang[17] proposed an optimal design of 4-level constant-stress ALT plans considering different censoring times. Chen et al.[18] discuss the optimal design of multiple stresses constant accelerated life test plan on non-rectangle test region. Fan and Yu[19] discuss the reliability analysis of the constant stress accelerated life tests when a parameter in the generalized gamma lifetime distribution is linear in the stress level.
The concept of geometric process (GP) was first introduced by Lam in 1988[20, 21] when he studied the problem of repair replacement. The statistical inference for geometric process is studied in both nonparametric and parametric ways. Lam and Zhang[22] introduced the geometric process model in the analysis of a two-component series system with one repairman. Huang[23] utilizes the geometric process in the analysis of accelerated life test with complete and censored exponential samples under the constant stress. Chan, Lam, and Leung[31] estimated the parameters of the GP with Gamma distribution by parametric methods including maximum likelihood method along with some nonparametric methods previously proposed by Lam. Chen[32] provided the Bayesian approach to the estimation of parameters in a GP with several popular life distributions including the exponential and lognormal distributions. Large amount of studies in maintenance problems and system reliability have shown that a geometric process model is a good and simple model for analysis of data with a single trend or with multiple trends. So far, there is no study that utilizes the geometric process in the analysis of accelerated life test with censored data.
In this paper, the geometric process is used for the Frechet distribution for constant stress with complete data. Constant stress is most simple and is also verified for some materials and products. It is also easy to maintain constant stress.

THE MODEL AND TEST PROCEDURE
A. The geometric process
Image
Image
Image

MAXIMUM LIKELIHOOD ESTIMATION
Many methods for estimating parameters exist but mainly maximum likelihood is used as it is easy to handle and gives the estimates of parameter with good statistical properties.
The likelihood function for the Frechet geometric process model based on the observed data in a total stress levels in accelerated life testing, can be written as
Image

FISHER INFORMATION MATRIX & ASYMPTOTIC CONFIDENCE INTERVAL
A. Fisher Information Matrix
The Fisher information matrix is obtained by taking the expected value of second and mixed partial derivatives of log( L) with respect to α, θ and λ. Unfortunately the exact mathematical expression for the expectation is very difficult to find. So, it can be approximated to the negative of second and mixed derivatives of the natural logarithm of the likelihood function evaluated at the MLE. The asymptotic Fisher Information matrix is given by:
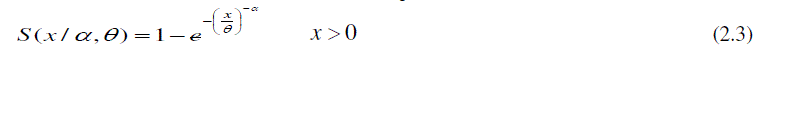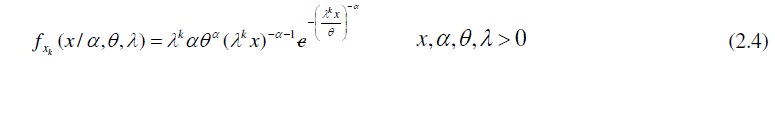Image
Image
Image

CONCLUSION
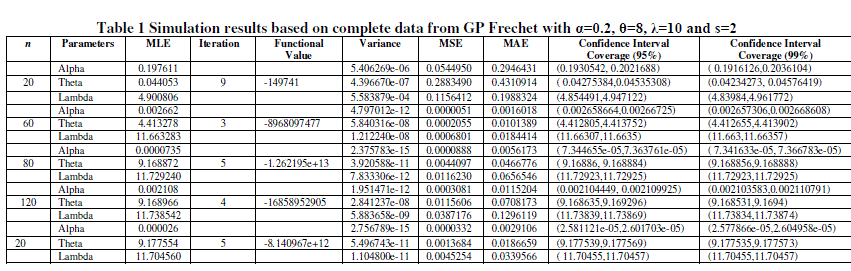
In this study, we introduced the geometric model for the analysis of accelerated life testing under constant stress when the life data are from a Frechet distribution .Geometric process model is a better choice as a reason of its simple nature, since it doesn’t require a log- linear function of life and stress to reparameterize the original parameter.The MLEs, MSEs and MAEs of the model parameters were obtained. Based on the asymptotic normality, the 95% and 99% confidence intervals of the model parameters were also obtained.
Results in Table 1 and 2 indicate that the estimation of α and λ are more appropriate than θ. The proposed estimator θˆ is consistently smaller than the true value of θ which means we tend to overestimate the mean lifetime of product at normal stress level. The result shows that when sample size increases, the variability of MLE becomes smaller and the confidence interval becomes narrower. For few cases confidence interval is précised to single value i.e. we get the exact value of estimators.
The results in Table 2 indicate that most of the estimates from the geometric process model match the values obtained by the log linear model. It is seen that when the sample size and number of stress levels are relatively small, some of the estimates obtained by geometric process model have a smaller mean square error and absolute square error than that obtained by the log linear model.From these results it may be concluded that the present model works well under complete data.

References
  1. Yurkowski, W., Schafer, R. E., and Finkelstein, Accelerated Testing Technology, Rome Air Development Center Tech.Rep., (1967),pp. 67-420.
  2. Nelson, W.B., Analysis of Accelerated Life Test Data with a Mix of Failure Modes by Maximum Likelihood, General Electric Co. Corp. Research & Development Tis Report”,(1974), pp. 74-160.
  3. Meeker, Jr., W.Q., Bibliography on Accelerated Testing, Statistics Univ., lowa State Univ., Ames, IA 50011,vol. 515, (1974), pp.294-5336.
  4. Viertl,R., Statistical Methods in Accelerated Life Testing, Vandenhoeck & Ruprecth,Gottingen, (1988).
  5. Lawless,J.F., Statistical Models and Methods for Lifetime Data, Wiley,New York, (1982).
  6. Cox, D.R., and Oakes, D., Analysis of Survival Data, Methuen(Chapman and Hall), New York, (1984).
  7. Lipson, C., and Sheth, N. C., Statistical Design and Analysis of Engineering Experiments, McGraw-Hill, New York, (1973).
  8. W. J. Owen , Accelerated test models using the Birnbaum-Saunders distribution, Ph.D. Thesis, Department of statistics, Faculty of Science, University of South Carolina, U.S.A”, (1997).
  9. D. S. Chang, L. C. Tang, Reliability bounds and critical time for the Birnbaum-Saunders distribution, IEEE Transactions on Reliability, vol.42, (1993).,pp. 464-469.
  10. D. J. Dupuis, J. E. Milles, Robust estimation of the Birnbaum-Saunders distribution, IEEE Transactions on Reliability, vol. 47, (1998)., pp.88- 95.
  11. A. Xu, Y. Tang, Bayesian analysis of Birnbaum-Saunders distribution with partial information, Computational Statistics and Data Analysis, vol.55, (2011).,pp. 2324-2333.
  12. A. Xu, Y. Tang, Reference analysis for Birnbaum-Saunders distribution,Computational Statistics and Data Analysis, vol. 54, (2010), pp. 185- 192.
  13. J. R. Rieck, Parametric estimation for the Birnbaum-Saunders distribution based on symmetrically censored samples, Communications in Statistics – Theory and Methods,vol. 24, (1995), pp. 1721-1736.
  14. S.L. Jeng, Inference for the fatigue life model based on the Birnbaum-Saunders Distribution, communications in statistics – simulation and computation, vol. 32, (2003), pp. 43-60.
  15. H. K. Ng, D. Kundu and, N. Balakrishnan , Point and interval estimation for the Two-parameters Birnbaum-Saunders distribution based on type-II censored samples, Computational Statistics and Data Analysis, vol. 50, (2006),pp. 3222-3242.
  16. Z. Wang, A.F. Desmond and X. Lu, Modified censored moment estimation for the two- parameter Birnbaum-Saunders distribution, Computational Statistics and Data Analysis, vol. 50, (2006), pp. 1033-1051
  17. Yang, G. B., Optimum constant-stress accelerated life-test plans, IEEE Transactions on Reliability, vol. 43, no. 4, (1994), pp. 575-581 Chen, W., Gao, L., Liu, J., Qian, P. and Pan, J., Optimal design of multiple stress constant accelerated life test plan on non-rectangle test region, Chinese Journal of Mechanical Engineering, vol. 25, no. 6, (2012), pp. 1231-1237,
  18. Fan, T. H. and Yu, C. H., Statistical Inference on Constant Stress Accelerated Life Tests under Generalized Gamma Lifetime Distributions, Quality and Reliability Engineering International, (2012),
  19. Islam, A. and Ahmad, N., Optimal design of accelerated life tests for the Weibull distribution under periodic inspection and type I censoring, Microelectronics Reliability, vol. 34, no. 9, (1994), pp. 1459-1468,
  20. Ahmad, N. and Islam, A., Optimal accelerated life test designs for Burr type XII distributions under periodic inspection and type I censoring, Naval Research Logistics, vol. 43, (1996), pp. 1049-1077,
  21. Lam, Y. and Zhang, Y. L., Analysis of a two-component series system with a geometric process model, Naval Research Logistics, vol. 43, no. 4, (1996), pp. 491-502
  22. Huang, S., Statistical inference in accelerated life testing with geometric process model, Master’s thesis, San Diego State University, (2011),
    23. Pan, Z., N. Balakrishnan, and Quan Sun, Bivariate constant-stress accelerated degradation model and inference, Communications in Statistics- Simulation and Computation, vol. 40, no. 2, (2011), 247–257,
  23. Watkins, A.J. and John, A.M., On constant stress accelerated life tests terminated by Type II censoring at one of the stress levels, Journal of Statistical Planning and Inference, vol. 138, no. 3, (2008), pp 768-786,
  24. Ahmad, N., Islam, A. and Salam, A., Analysis of optimal accelerated life test plans for periodic inspection: The case of exponentiated Weibull failure model, International Journal of Quality & Reliability Management, vol. 23, no. 8, (2006), pp. 1019-1046
  25. Ahmad, N., Designing Accelerated Life Tests for Generalized Exponential Distribution with Log-linear Model, International Journal of Reliability and Safety, vol. 4, no. 2/3, (2010), pp. 238-264,
  26. Lam, Y., Geometric process and replacement problem, Acta Mathematicae Applicatae Sinica, vol. 4, no. 4, (1988), pp. 366-377
  27. Zhang, Y. L. (2008): A geometrical process repair model for a repairable system with delayed repair, Computers and Mathematics with Applications, vol. 55, no. 8, (2008), pp. 1629-1643,
  28. Kamal, M., Zarrin, S., Saxena, S. and Islam, A., Weibull Geometric Process Model for the Analysis of Accelerated Life Testing with Complete Data, International Journal of Statistics and Applications, vol. 2, no. 5, (2012), pp. 60-66,
  29. J. S. Chan, Y. Lam, AND D. Y. Leung, Statistical inference for geometric processes with gamma distributions, Computational Statistics and Data Analysis,vol. 47, (2004), pp. 565–581.
  30. J. Chen, Bayesian computation for geometric process in maintenance problems, Mathematics and Computers in Simulation, vol. 81, (2010), pp. 771–781.
  31. R Development Core Team (2008). R: A language andenvironment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria.