International Journal of Innovative Research in Science, Engineering and Technology
MenuISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Imran Ahemad Khan1, G. K. Awari2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Vibration analysis of plates has been an active research subject of engineering field. The analytical solutions have been found for plates with specified forms of mass and stiffness modifications, but for the plates with uncertain mass and stiffness modifications have not been addressed confidently. The concept of uncertainty plays an important role in the design of practical mechanical system. So it becomes important to study its effects on mechanical system for different frequency domain i.e. low, medium and high frequency. Here in this paper structural element square plate with all edge fixed boundary condition is selected on which mass, stiffness and combination of it, uncertainty is taking in account. By using Finite Element Method technique finding out, how plate is dynamically behaves in vibration. During modal analysis natural frequency and mode shapes are find and compared the response of bare plate and the plate with mass, stiffness ,mass-stiffness combination uncertainty.
Keywords |
| Vibration analysis, FEM, Modal Analysis, Uncertain parameters and Ansys software. |
INTRODUCTION |
| Plates and plate-like components are widely used in engineering structures such as several machine structures, civil engineering structure, boards in electronic equipment. Vibration analysis of plates and plate-like components has been an active research subject and numerous technical papers have been published. For to calculating the natural frequencies and mode shapes of a structure Modal analysis method is used. This method determined the dynamic response of complicated structural dynamic problems. In general, applications of modal analysis today cover a broad range of objectives identification and evaluation of vibration phenomena, validation, structural integrity assessment, structural modification, and damage detection. In engineering design, it is important to calculate the response quantities such as the displacement, stress, vibration frequencies, and mode shapes of given set of design parameters. The study of mathematical models which involve physical and geometric parameters such as mass density ρ, elastic modulus E, Poisson’s ratio v, lengths, and cross-section shape characteristics. In many practical engineering applications, these parameters frequently do not have well-defined values due to non-homogeneity of the mass distribution geometric properties or physical errors, as well as variation arising from the assembly and manufacturing processes. In engineering design these uncertainties in material properties, geometric parameters and boundary conditions are often unavoidable and must be considered. This concept of uncertainty plays an important role in investigation of various engineering problems. |
II. LITERATURE SURVEY |
| Natural frequencies and mode shapes of the modified plate are identified by analysing the receptance data based on the concept of modal analysis [1]. A more recent and complete review of vibration of plates can be found in Ref. [2].However, for most cases where plates are used in practical engineering structures, mass and/or stiffness modifications of these plates become necessary, while the natural frequencies and mode shapes of the modified plates are of interest. Such problems of determining the natural frequencies and mode shapes of a plate with mass and/or stiffness modifications has been treated by several investigators. By assuming the fundamental shape function and using the Rayleigh-Ritz method, fundamental natural frequency of a rectangular plate with a rigid mass of finite width under certain boundary conditions was calculated by Cohen and Handelman [3]. The fundamental frequency of a square plate clamped all around and having a mass at the center of twice its own mass was solved by Solecki [4]. Stokey and Zorowski [5] developed a general method for determining approximately the natural frequencies of a rectangular plate with arbitrarily located masses. The study of mathematical models which involve physical and geometric parameters such as mass density ρ, elastic modulus E, Poisson’s ratio v, lengths, and cross-section shape characteristics. In many practical engineering applications, these parameters frequently do not have well-defined values due to non-homogeneity of the mass distribution geometric properties or physical errors, as well as variation arising from the assembly and manufacturing processes, structural loading and environmental conditions [6]. In engineering design these uncertainties in material properties, geometric parameters and boundary conditions are often unavoidable and must be considered. This concept of uncertainty plays an important role in investigation of various engineering problems [7]. Here in this paper square plate with all edge fixed boundary condition and two major uncertain parameters are consider i.e. mass and stiffness. Hence the analysis is done on bare plate and plate with uncertainty due to mass, stiffness and combination of mass and stiffness. For all these combination modal analysis is done and different natural frequency and mode shapes were found. Again for these combinations harmonic analysis is done and FRF were plotted and compared it for all the conditions. |
III. MATHEMATICAL MODELING |
| All the Vehicles, aircraft and home appliances structures are made up of Plate or combination of Plates so it becomes necessary to study Plate vibration. Using the Lagrange- Rayleigh -Ritz technique [8], the equations of motion of a dynamic system in modal space can be derived. 3.1: Bare Square Plate: Considering the All Edge Fixed bare square plate (with no structural uncertainty). For this plate eigenfunction is described by sinusoidal mode shapes in the x and y directions, respectively. |
 |
Lagrange’s equation results in the equation of motion of the bare plate as given below
 (1)
The natural frequencies can then be obtained by eigenvalue analysis [9]
3.2: Uncertain Mass Loaded Plate:
Now consider the uncertain mass loaded plate as shown in Fig 2 for this the equation of motion is |
 |
 |
 |
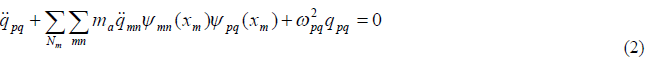V. EFFECT OF UNCERTAIN PARAMETERS ON THE NATURAL FREQUENCY AND MODE SHAPE |
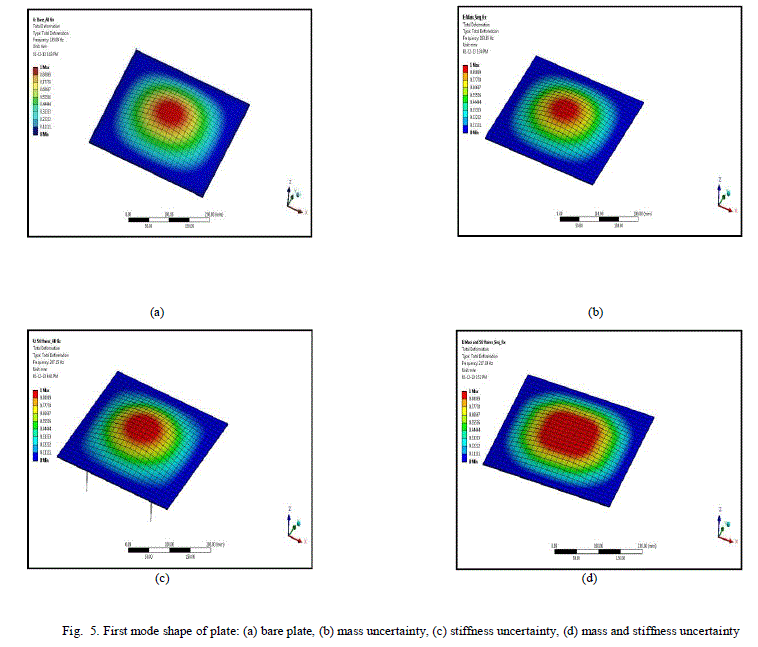
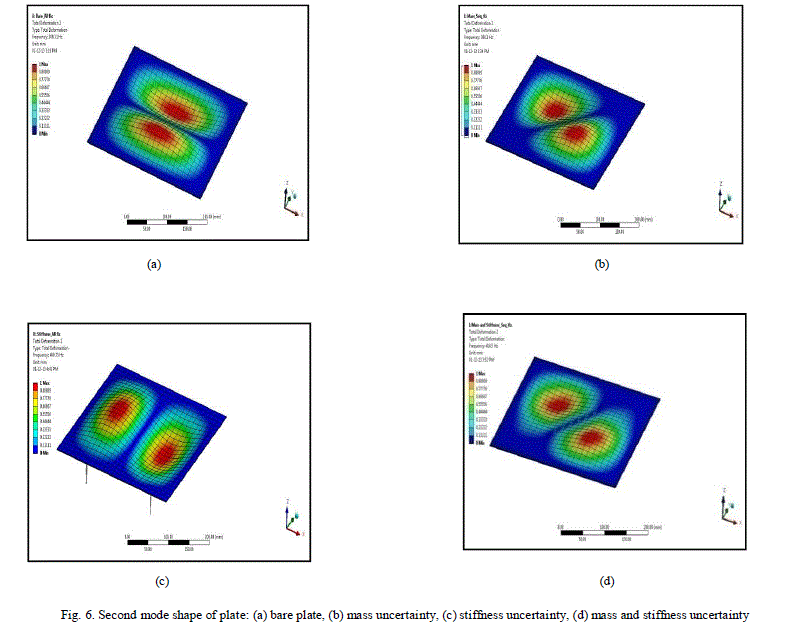
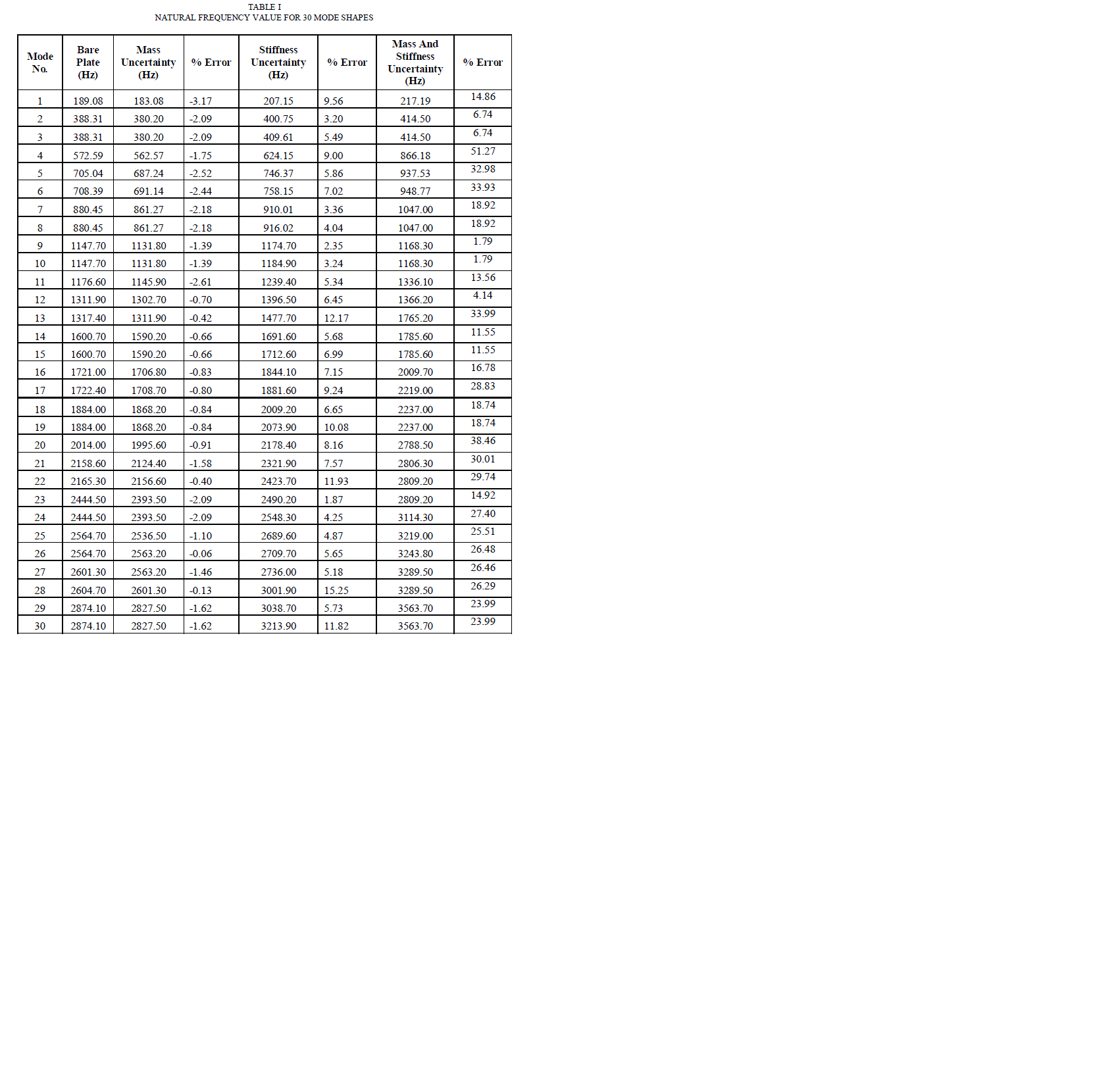
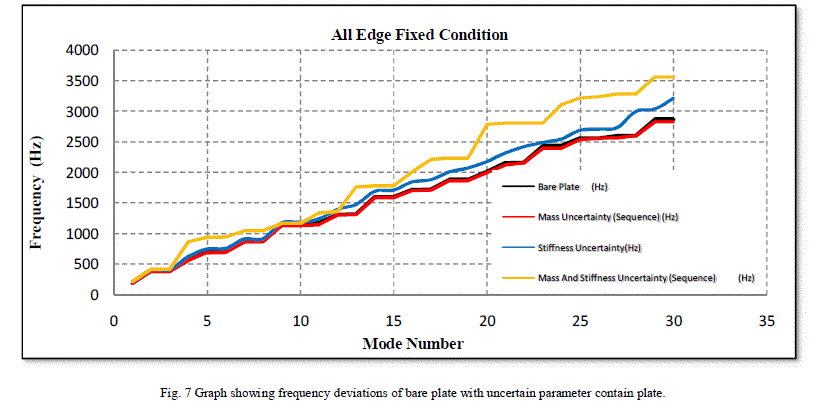
| The frequency range is taken from 0 Hz to 3000Hz. Plate is exited for 30 modes The solver used is Block Lanczos [11]. It gives 30 natural frequency values for bare plate, mass uncertainty plate, stiffness uncertainty plate and combination of mass and stiffness uncertainty plate shown in the Table 1. and also in Fig 5 and Fig 6. Natural frequency get reduces due to mass uncertainty and its percentage decreased by -3.17% is shown in Table 1. Due to stiffness uncertainty natural frequency very prominently increases by 9.56% and the combination of mass and stiffness is increase by 14.87%. These are the effects of uncertainty on the natural frequency. In the first mode there is change in mode shape obtained as shown in Fig 5(a) is compare with Fig 5 (b), (c), (d) as the red colour dimple size is changing. In the second mode as compare with Fig 6(a), in Fig 6 (b) due to mass uncertainty mode shape is changed. Due to stiffness phase is changed as shown in Fig 6(c) and (d). These effects of uncertainty on the mode shapes were found. Fig 7 showing frequency deviations of bare plate with uncertain parameter contain plate. |
 |
 |
 |
 |
VI. CONCLUSIONS |
| By adding the uncertain mass, we are getting the different dynamic characteristic of plate for the same boundary condition. Though, the amount of uncertain mass is very low still it has influence on the structure. First frequency of the plate has been shift from 189.08 Hz to 183.08 Hz in case of all edge fixed boundary condition. It is clearly showing the effect of addition of uncertain mass. This trend of decreasing the plate frequencies are continuing for all the modes. If we compare the characteristics of bare plate with that of plate with uncertain for the first 30 modes, there is clear deviation in frequency shift which may affect the working condition of entire structure. In case of uncertain mass in sequence pattern there is a deviation of -3.17% in fundamental mode which may not be acceptable in case precise instrumentation or precision manufacturing systems. Addition of uncertain mass to the bare plate not only shift its frequencies but it also affects the mode shapes of plate. By adding an uncertain mass to the plate structure, apart from fundamental mode, most of the modes are losing their pattern. Irrespective of the frequency shift, the changing vibrating behavior of plate itself is a critical and unavoidable issue. Addition of the uncertain stiffness dominatingly changes dynamic characteristic of plate for the same boundary condition. First frequency of the plate has been shift from 189.08 Hz to 207.15 Hz in this boundary condition having the deviation of 9.55% in fundamental mode which may not be acceptable. By adding the uncertain mass and stiffness, we are getting the drastically different dynamic characteristic of plate for the same boundary condition. First frequency of the plate has been shift from 189.08 Hz to 217.19 Hz in case and deviation of 14.86 % in first mode and in forth mode it is 51.27% of fundamental mode which may not be acceptable in any case. |
VII. ACKNOWLEDGEMENTS |
| The authors acknowledge with tanks to the Department of Mechanical Engineering of Priyadarshini College of Engineering, Nagpur for their support during this research work. |
References |
|