Application of Genetic Algorithm in
Interplanetary Trajectory Design

S.Mahendran; ML.Mahadevan

Application of Genetic Algorithm in Interplanetary Trajectory Design

S.Mahendran¹, ML.Mahadevan²

PG Scholar, Thiagarajar College of Engineering, Madurai, India
Assistant Professor, Thiagarajar College of Engineering, Madurai, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

For a given set of celestial bodies, the problem of finding an optimal sequence of gravity assist and the transfer arcs connecting the elements of the set is of combinatorial in nature. The number of possible paths grows exponentially with the number of celestial bodies. Therefore the design of an optimal gravity assist trajectory is a NP-hard mixed combinatorial continuous problem. An exhaustive search of the space of input variable is unaffordable even with modern state of art computing technology. Thus a feasible approach requires artificial intelligence (AI) and modern optimization techniques based on the intelligence selection of some potential solutions. These individuals evolve in order to generate better solution until some optimization criterion is met. Here the goal of this work is to find the trajectory which uses gravity assist maneuvers to reach the target planet (Jupiter), spending minimal fuel with minimal time for the travel. In this work, the model has been formulated, as a preliminary mission design for an interplanetary trajectory from earth to Jupiter via gravity assist at mars, which proposed to use genetic algorithm with multi objective to optimize the trajectory which has minimal fuel consumption and minimal time.

INTRODUCTION

A spacecraft launching from Earth will start within the sphere of influence (SOI) of Earth. As the spacecraft Exits Earth’s SOI it enters the Sun’s SOI until it enters the SOI of another celestial body. While the spacecraft is Inside the SOI of a celestial body such as the Earth or Sun the effects of all other celestial bodies can be ignored (as First approximation) and the dynamics can be modeled as a two-body gravitational system. By patching together a sequence of such twobody problems a complete trajectory can be determined. A trajectory such as that of one from Earth to Mars may be represented by a combination of the following three two-body problems: Spacecraft and Earth, Spacecraft and Sun, spacecraft and Mars. We can take advantage of the effects of a spacecraft passing near a celestial body that is not its destination body. This is known as a planetary flyby or gravity assist. Spacecraft trajectory optimization is a global optimization task in its nature. The application of global optimization techniques to the design of interplanetary trajectories has received quite some attention in the past years as it becomes increasingly evident that such a framework introduces a high level of automation in a process that is otherwise still heavily relying on expert engineering knowledge. Many interplanetary trajectory design problems can be stated as optimization problems, where one of the fundamental goals is the maximization of the spacecraft mass available for the payload, equivalent to a minimization of the propellant necessary on board. It is very difficult to make fair comparisons between optimal trajectories as the constraints and objectives used in the optimization are many and often not clearly stated or mathematically defined. On the other hand a number of algorithms and approaches to global trajectory optimization have been proposed, are already available in the literature or are being developed and it is indeed extremely interesting to be able to compare them.

LITERATURE REVIEW

Zotes (2010) used Genetic Algorithm to optimize the ascent trajectory of conventional two stage launcher with the mission to reach the highest possible stable circular Low Earth Orbit & to maximize the speed of the tangential escape trajectory. Zotes (2012) proposed the use of Particle Swarm Optimization with single objective and multi objective. Here the tuning parameters are launch epoch and the time of flight between the planets, and then the results are compared with other works in the references. Vasile (2010) Analyses the performance of a global search algorithm on a no of space trajectory problems, starts with some evolutionary heuristics in the form of discrete dynamical system. Yam (2011) Sims – Flanagan transcription model is proposed to model low thrust trajectory design as a constrained global optimization problem. Solvers applied are Basin Hopping and simulated annealing which is hybridized with local search. Olympio (2011) multiple asteroid mission problems have been taken into consideration with indirect optimization. Algorithm is implemented with parellization for computational speed. Zhang (2013) low energy low thrust transfer with Particle Swarm Optimization is used on the criterion of smallest velocity discontinuity and limited position discontinuity. Then The fuel optimal problem is formed using Calculus of variation and pontyagin’s maximum principle. Venditti (2010) interplanetary trajectory with multi objective is considered for minimum fuel and minimum time. The methodology they proposed is the non inferiority criterion and the smallest loss criterion. Cerrito (2010) Proposed autonomous planning and scheduling system for multi gravity assist trajectories, which uses the Ant Colony Optimization for the mission to Saturn with flyby at Jupiter. Berend (2012) this paper explores the problem of optimization of power limited propulsion system with the mission to mars is considered (Magneto Plasma).Novak (2011) Novel Shaping Method has been used to the mission to mars Neptune and asteroid 1989ML. Vasile (2011) a variant of differential evolution is derived with the assumption of differential mutation strategy is applied in this work. Cerrito (2010) modified Ant Colony Optimization is applied to the multi gravity assist autonomous planning and schedule of events to mercury and Saturn with flyby in Venus and Jupiter.

Schuetze (2011) multi objective space mission design problem for several low thrust multi gravity assist trajectory is considered with Bi-impulse transfer is accommodated in this paper. Addis (2011) Simplified model proposed by the European space agency as a test problem which solves the problem using funnel structure similar to that of molecular optimization problem. Thus from the above literature survey that what we observe is that the application of global optimization techniques such as genetic algorithm, particle swarm optimization, Ant colony optimization, Differential evolution, Simulated Annealing algorithm, Hybrid Optimization Methods has been extensively used in the design and analysis of the spacecraft trajectory. But most papers described above only considered the single objective function for the spacecraft trajectories to the interplant’s that is minimization of the fuel(in terms of Change in velocity Δv) used in the spacecraft. Few papers have multiobjective functions for this kind of problem. But the evolutionary algorithms are not extensively used in multi objective optimization. Hence in this paper genetic algorithm will be used to address the gravity assist trajectories with multi objective functions of both change in velocity and the time taken to reach the target planet.

PROBLEM FORMULATION

To properly transcribe this problem in the form of generic optimization problem we must find a set of state variables x that are unambiguously related to each possible trajectory that can be own. Starting from the Earth, we let the starting date tE, the outgoing Planetocentric velocity VE and its direction to be free parameters.

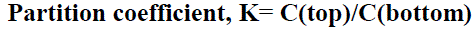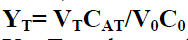METHODOLOGY

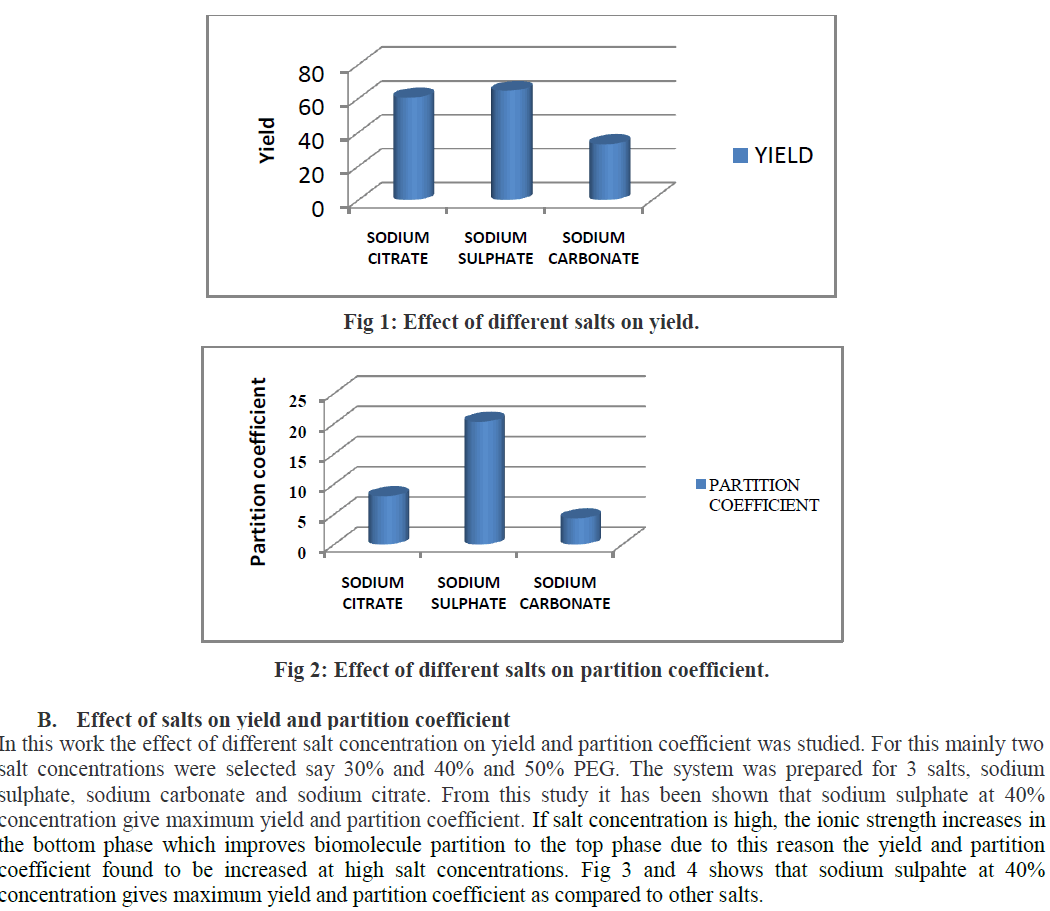
A Genetic Algorithm uses probabilistic selection as a basis for evolving a population of problem solutions. An initial population is created and subsequent generations are created according to a pre-specified breeding and mutation methods inspired by nature. The points in the population are randomly selected to be n. The n points (Random Number’s) are generated using random number generator then we select the selection, crossover, mutation operators& then we set the termination criteria.

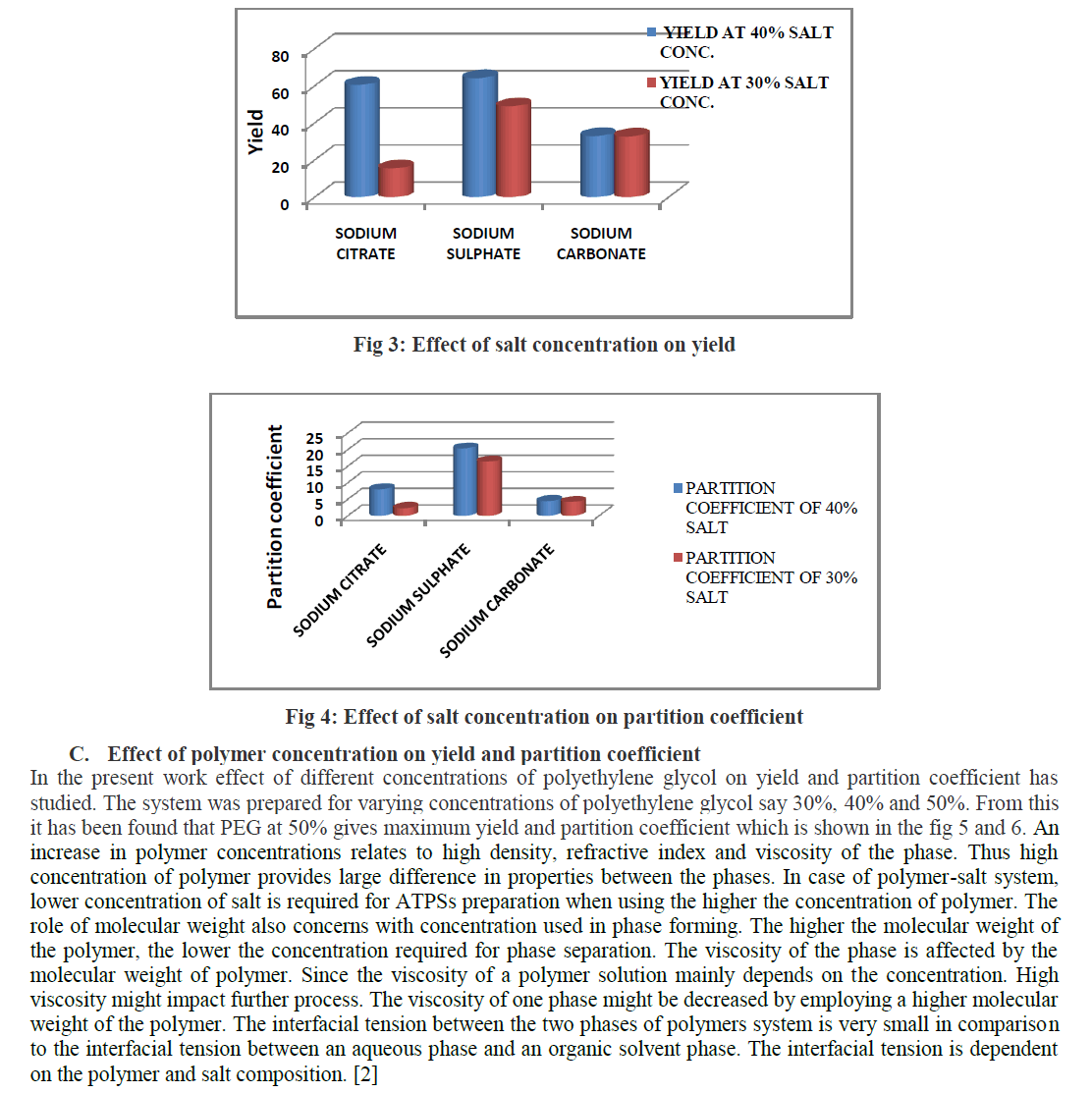
RESULTS AND ANALYSIS

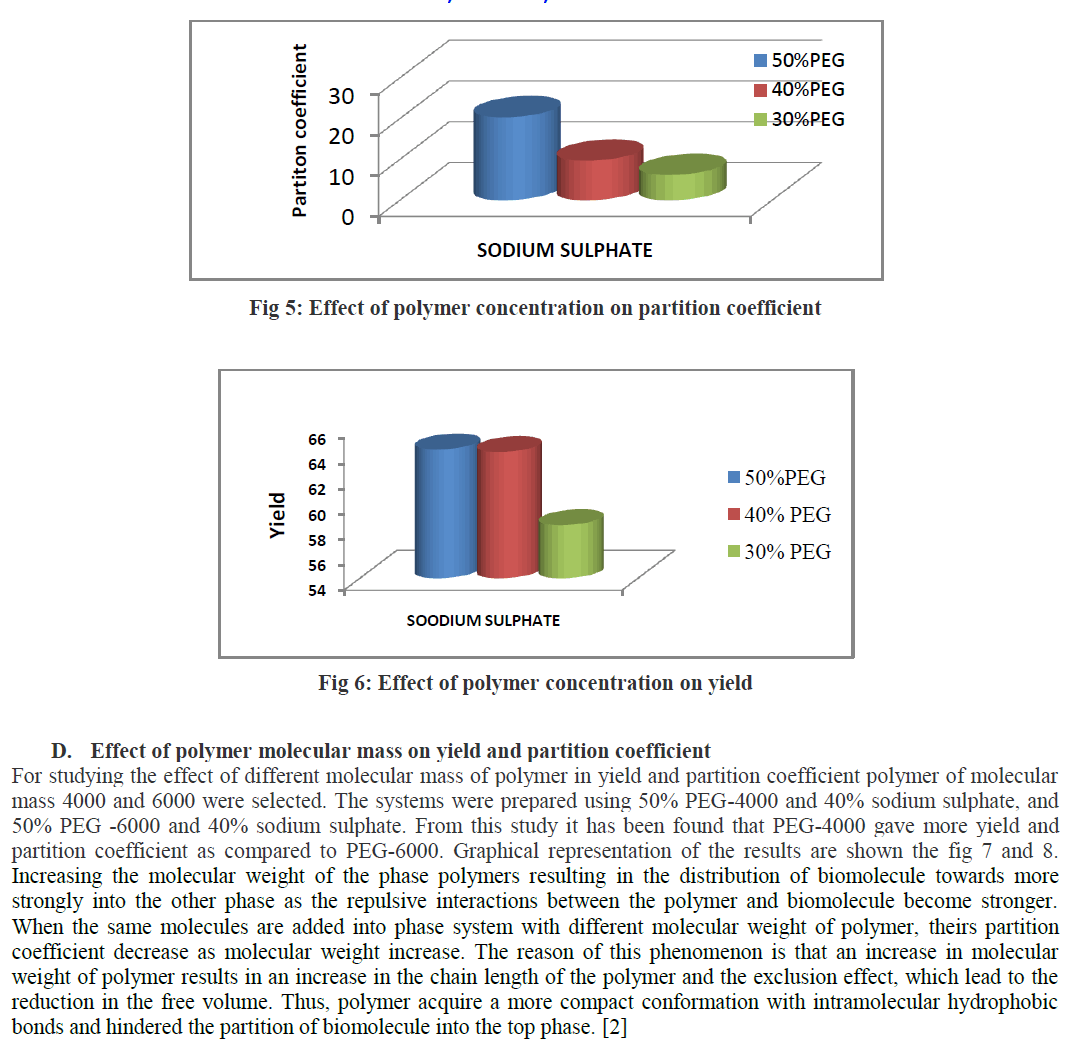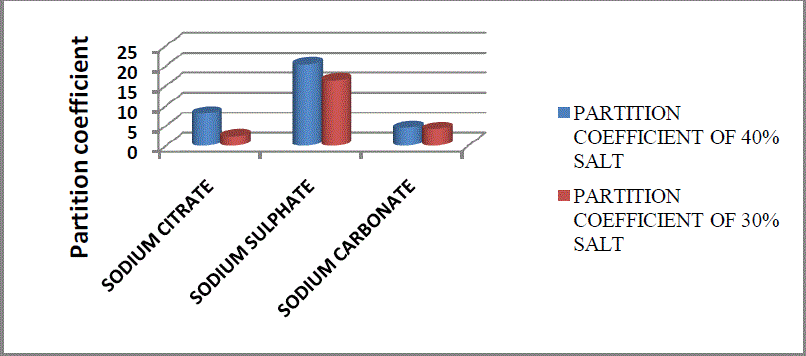CONCLUSION & FUTURE SCOPE

The goal of the GA is to minimize the Total Delta v (change in velocity) and the time taken to reach the target planet in the interplanetary mission. The tuning parameters are the launch epoch and the time of flight between two consecutive planets. From the analysis performed we can say that the algorithm is reliable in that it converged on every run. This algorithm did good results which are comparable to the previous work. In order to reduce the computational time hybridization of evolutionary algorithms must be applied for this kind of problems. In future look at the actual affects of the gravity assist in comparison to missions that do not utilize gravity assist, optimizing the weighting factors for the penalty functions, optimizing the number of segments to be made in each leg of the mission, Optimizing the genetic Parameters Plenty of work remains to improve this project.

References

Addis, B. et al., 2011. A global optimization method for the design of space trajectories. Computational Optimization and Applicationst Optim Appl, 48, pp.635–652.
Bérend, N., 2012. Optimum design of power-limited propulsion systems with application to fast Earth-to-Mars transfer. Acta Astronautica, 79, pp.107–117.
Battin R H, An Introduction to the Mathematics and Methods of Astrodynamics, Revised edition AIAA, New York, 1999.
Ceriotti, M. & Vasile, M., 2010. MGA trajectory planning with an ACO-inspired algorithm. Acta Astronautica, 67(9- 10), pp.1202–1217.
Ceriotti M, Vasile M., 2010. Automated Multigravity Assist Trajectory Planning with a Modified Ant Colony Algorithm. Journal of Aerospace Computing, Information, and Communication, 7(9), pp.261–293.
Gregory Lantoine, RyanP.Russell, Stefano Campagnola, Optimization of low-energy resonant hopping transfers between planetary moons, Acta Astronautica 68 (2011) 1361–1378
Olympio, J.T., 2011. Optimal Control Problem for Low- Thrust Multiple Asteroid Tour Missions. Journal of Guidance, Control, and Dynamics, 34(6), pp.1709–1720.
Schuetze, O. and Vasile, M. and Coello Coello, C.A., 2011. Computing the set of epsilon efficient solutions in multi objective space mission design. Journal of Aerospace Computing, Information, and Communication, 8(3), pp.53– 70.
Novak D.M, M.V., 2011. An Improved Shaping Approach to the Preliminary Design of Low thrust Trajectories. Journal of Guidance, Control, and Dynamics, 34(1), pp.128–147.
Vasile, M., Minisci, E. & Locatelli, M., 2011. An Inflationary Differential Evolution Algorithm for Space Trajectory Optimization. Evolutionary computation, 15(2), pp.267–281.
Vasile, M., Minisci, E. & Locatelli, M., 2010. Analysis of Some Global Optimization Algorithms for Space Trajectory Design. Journal of Spacecraft and Rockets, 47(2), pp.334– 344.
Venditti Flaviane Cristine Faria, Evandro Marconi Roccon, Antonio Fernando Bertachinide Almeida Prado, Alexander Suhkanov, Gravity-assisted maneuvers applied in the multiobjective optimization of interplanetary trajectories, Acta Astronautica 67 (2010) 1255–1271.
Yam, C.H., Lorenzo, D.D. & Izzo, D., 2011. Low-thrust trajectory design as a constrained global optimization problem. Journal of Aerospace Engineering, 225(11), pp.1243–1251.
Zotes Alonso, F. & Santos Peñas, M., 2010. Multi-criteria genetic optimisation of the manoeuvres of a two-stage launcher. Information Sciences, 180(6), pp.896–910.
Zotes Alonso, F. & Santos Peñas, M., 2012. Particle swarm optimisation of interplanetary trajectories from Earth to Jupiter and Saturn. Engineering Applications of Artificial Intelligence, 25(1), pp.189–199.
Zhang, P. et al., 2013. A low-thrust transfer between the Earth–Moon and Sun–Earth systems based on invariant manifolds. Acta Astronautica, 91, pp.77–88.