ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Dr. N. B. Chaphalkar1, Prashant P. Shirke2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In various stages of project lifecycle, decision making has vital and strategic importance. These decisions are related to different problems and one of the issues is related to selection of alternatives. Decisions made must be independent of any preference or influence. Improper or incorrect selections often increase duration and expenditure of project. The conventional methods for decision making are inadequate for dealing with the imprecise or vague nature of today‟s complex decision problems. To overcome this difficulty, in this paper use of fuzzy Multi-Criteria Decision Making (MCDM) methods is discussed. The aim of this study is to use fuzzy Analytic Hierarchy Process (AHP) and the fuzzy Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) methods for the selection of type of bridge. The proposed methods have been applied to selection of bridge type problem in Pune city. After determining the criteria that affect the selection of type of bridge decisions, fuzzy AHP and fuzzy TOPSIS methods are applied to the problem and results are presented. The similarities and differences of two methods are also discussed.
Keywords |
| Decision Making, MCDM, Fuzzy Logic, Fuzzy AHP, Fuzzy TOPSIS |
INTRODUCTION |
| In India, construction is the second largest economic activity next to agriculture. Construction accounts for nearly 65 per cent of the total investment in infrastructure and is expected to be the biggest beneficiary of the surge in infrastructure investment over the next five years. According to Indo-Italian report, €239.68 billion is likely to be invested in the infrastructure sector over the next five to 10 years; in power, roads, bridges, city infrastructure, ports, airports, telecommunications, which would provide a huge boost to the construction industry as a whole (Indo-Italian Chamber Report, 2008). Decision making is the study of identifying and choosing alternatives based on the values and preferences of decision maker [14]. As magnitude and scope of problem increases, decision making process gets more and more complicated, because with increase in size and scope, number of alternatives and related factors also increase [17]. Good quality highway network is very important for progress of the country and bridges are the vital part of any highway network. Bridges of various types and sizes were built in recent years in India. Defective decision making is one of the major reasons behind losses. (Report of Construction Industry Development Council India, 2006-07) [5]. This paper focuses on the study of new techniques of multi criteria for decision making namely fuzzy AHP and fuzzy TOPSIS for the selection of type of superstructure for bridge construction, where the ratings of various alternatives for the type of structure under various criteria and the weights of all criteria are represented by fuzzy numbers. Further the paper compares outputs given by both methods. |
MULTI-CRITERIA DECISION MAKING (MCDM) |
| MCDM constitutes an advanced field of operations research that is devoted to the development and implementation of decision support tools and methodologies to deal with complex decision problems involving multiple criteria, goals, or objectives of conflicting nature. The tools and methodologies provided by MCDM are not just some mathematical models aggregating criteria, points of view, or attributes, but furthermore they are decisionsupport oriented [17]. |
| The most preferable situation for a MCDM problem is when all ratings of the criteria and their degree of importance are known precisely, which makes it possible to arrange them in a crisp ranking. However, many of the decision making problems in the real world take place in an environment in which the goals, the constraints and the consequences of possible actions are not known precisely. These situations imply that a real decision problem is very complicated and thus often seems to be little suited to mathematical modelling because there is no crisp definition. Consequently, the ideal condition for a classic MCDM problem may not be satisfied, in particular when the decision situation involves both fuzzy and crisp data. In general, the term “fuzzy” commonly refers to a situation in which the attribute or goal cannot be defined crisply, due to the absence of well-defined boundaries of the set of observation to which the description applies [15]. Concept of fuzzy logic was introduced in 1965 by Prof. Lofti A. Zadeh, professor of computer science at the University of California in Berkelay. Basically fuzzy logic is a multivalued logic that allows intermediate values to be defined between conventional evaluations like true/false, yes/no etc. and notions like rather tall or very fast can be formulated mathematically in order to apply a more human like way of thinking [16]. |
CASE STUDY |
| For the application of MCDM techniques a bridge construction project in Pune city is selected. The site location already consists of two existing bridges over the river, but due to increased vehicle population and traffic load resulting into frequent traffic congestions the need for another bridge was necessary. The proposed bridge was to satisfy the following three needs: |
| Proposed bridge should solve the problem of traffic congestion in the area along with the elegant aesthetical appearance. |
| Service life of existing bridges on site is over and the new bridge has to replace old bridges. |
| The site contains old bund on river, recently new spillway gates are constructed for the bund. Proposed bridge should provide an access point for the maintenance of the spillway gates. |
| Considering needs of the problem and using site data, decision problem is constructed as “Select type of superstructure for proposed bridge”. To solve decision problem, a methodology is prepared using fuzzy AHP and fuzzy TOPSIS methods. These methods require input in the form of verbal judgments from people working in the field. To accomplish the task, a panel of six experts was organized wherein the experts were selected on the basis of their experience in field of bridge construction. |
IDENTIFICATION OF CRITERIONS AND DEVELOPMENT OF ALTERNATIVES |
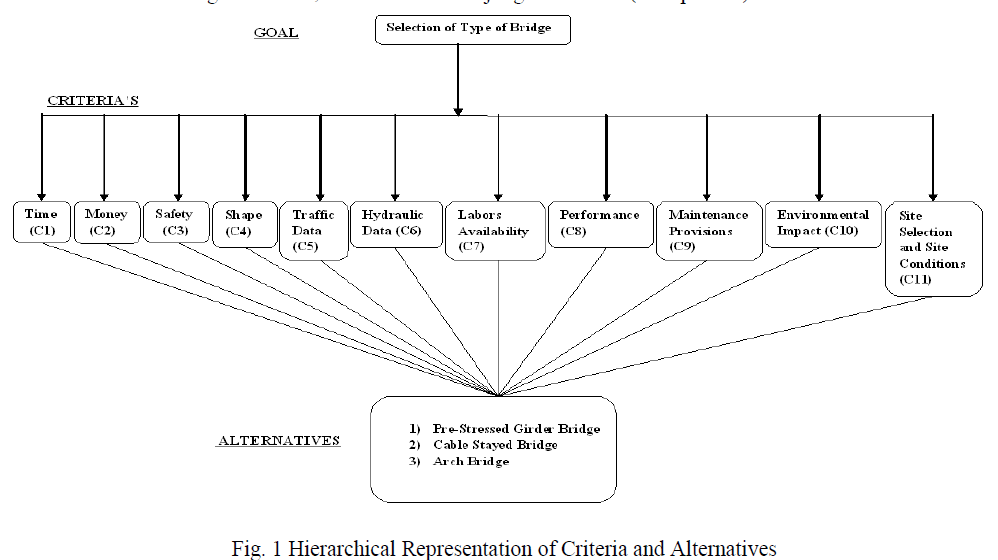
| First step of the proposed methodology is to identify important criteria affecting the choice of superstructure and develop best possible alternatives for the project. For the identification of criteria Delphi technique is used. Eleven top rated criteria were selected which included time, money, safety, shape, traffic data, hydraulic data, labour availability, performance, maintenance provisions, environmental impact, site selection and site conditions. For the development of alternatives for type of bridge, extensive study of decision problem is required. Local authority had done the study through various consultancies and considered three alternatives regarding type of bridge. For the study the same alternatives are taken under consideration. The three alternatives considered namely Pre-stressed Girder Bridge, Cable Stayed Bridge, and Arch Bridge for the study. |
A. Solution by fuzzy AHP |
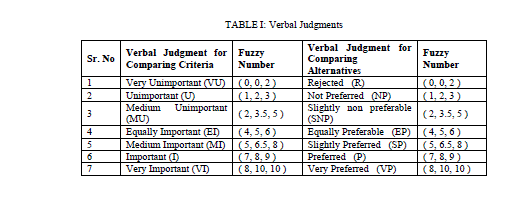
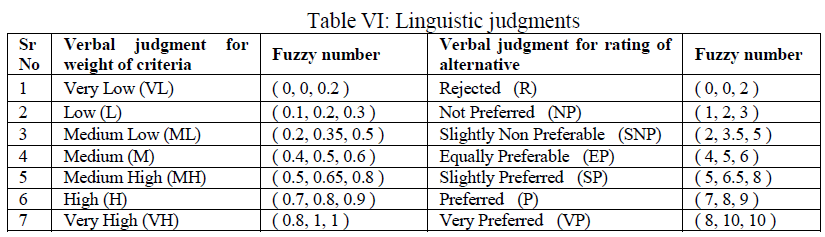
| First proposed by [1] the analytic hierarchy process (AHP) is a widely used multiple criteria decision-making tool. For this paper fuzzy AHP method is proposed for the selection problem of the type of bridge. Six decision-makers evaluated the importance of criteria and alternatives by using the linguistic variables in Table 1. |
 |
| Step 1: Construction of hierarchy |
| The first step of the AHP method is to determine all the important criteria, possible alternatives and define their relationship in the form of a hierarchy as shown in Figure 1. According to [4], fuzzy TOPSIS algorithm is capable of handling only single tier problems, while fuzzy AHP can handle more than one tier problems. |
| Step 2: Evaluation of fuzzy pair wise comparisons |
| Questionnaire for fuzzy AHP is prepared keeping in mind type and nature of input required to solve the problem. Questionnaires are filled through direct communication with the panel of experts. Definition of the hierarchical relation is followed by pair wise comparisons of all the criteria on the same level of the hierarchy. The pair wise comparison is performed by using linguistic terms given in Table 1. The fuzzy sets used for this study are taken from [4]. |
| Step 3: Construction of fuzzy decision matrix |
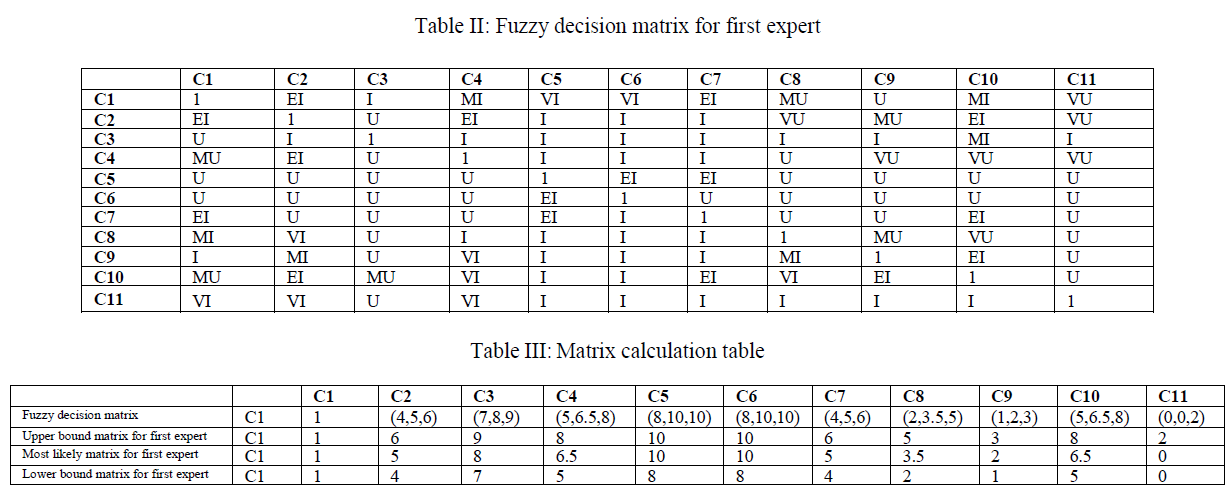
| After the evaluation of criteria and alternatives using linguistic variables, the fuzzy decision matrix as shown in table 2 is constructed for each of the expert. The values in the upper triangular matrix are filled by using the expertâÃâ¬ÃŸs judgments and the lower triangular matrix is filled by using the reverse of the verbal judgements. For e.g. the verbal judgement of comparison between criterion C1 (time) and C3 (safety) is „IâÃâ¬ÃŸ (important) in upper triangular matrix whereas in the lower triangular matrix, the reverse verbal judgment is „UâÃâ¬ÃŸ (unimportant). |
 |
| Each verbal judgment in the decision matrix represents a triangular fuzzy set given in Table 1 which is used for further calculations shown in Table 3. To facilitate fuzzy weight calculations, above matrix in Table 2 is further divided in Upper bound matrix (AU), Most likely matrix (AM), Lower bound matrix (AL). Upper bound matrix represents the higher values in the set. For example in the fuzzy set (4, 5, 6) for „Equally ImportantâÃâ¬ÃŸ verbal judgement, the upper bound value is 6, most likely value is 5 and the lower bound value is 4. Table 3 shows the triangular fuzzy set for the first row of the Fuzzy Decision Matrix for First Expert whereas Table 4, 5 and 6 show the first row of each of the upper bound matrix (AU), most likely matrix (AM), lower bound matrix (AL) for first expert. |
 |
| Step 4: Construction of element weight |
| Normalization of Geometric Mean Method (NGM) is used to calculate element weights of criteria by using the equation |
| In the equation, |
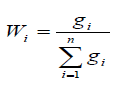 |
| gi = Geometric mean of criterion i. |
| rij = Comparison value of criterion i to criterion j. |
| wi = ith criterion weight. |
| Step 4.1: Calculation of Geometric Mean |
| For Upper Bound Matrix AU, Geometric Mean for Time (C1) criteria from row C1 of Table 4 is calculated as u1 = (1 x 6 x 9 x 8 x10 x 10 x 6 x 5 x 3 x 8 x 2) ^ (1/11) = 5.1113 |
| The Geometric Mean of other criteria calculated in upper bound matrix, are summarized in Table 3. |
| Step 4.2: Calculation of element weight |
| Using NGM, element weight for Time criterion is calculated as 0.0981. Similarly the element weights are calculated for other criteria in upper bound matrix, most likely matrix and lower bound matrix from first expertâÃâ¬ÃŸs decision matrix which are summarized in Table 4. |
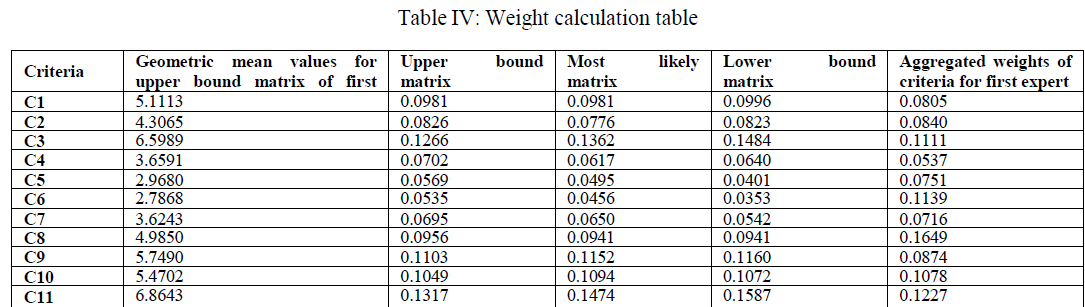 |
| Step 4.3: Identify minimum, mean and maximum element weight |
| After the calculation of the element weight, minimum, mean and maximum element weight from Table 4 for each of the criteria is identified. E.g. Minimum, mean and maximum element weight for Time (C1) are (0.0981, 0.0981, 0.0996). Similarly steps 3 and 4 are repeated for other experts. |
| Step 5: Aggregation of Experts Decision |
| As the responses are obtained from six experts they are aggregated into one by using the centre of sum method. Equation of centre of sum method is represented as |
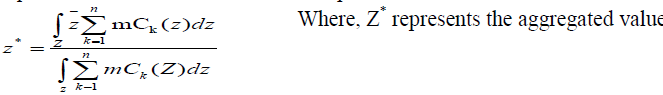 |
| For Time (C1) criteria, aggregated value is calculated as 0.0805 by using above equation. The calculated aggregated weights of other criteria are summarized in Table 5. These results show that „Performance of particular type of bridge (C8)âÃâ¬ÃŸ is most dominating criteria in the selection process followed by „site selection and site conditionsâÃâ¬ÃŸ. Steps 3 to 5 are followed for calculating aggregated weights of all alternatives with respect to all criteria. The results are summarized in Table 5: |
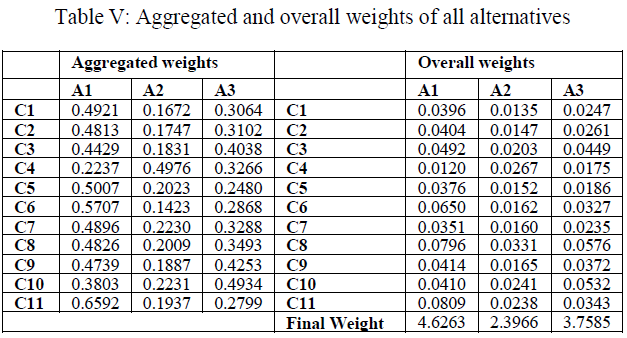 |
| Step 6: Calculation of Overall Weight of each alternative |
| Now overall weight of each alternative is calculated by multiplying weight of main criteria with local weight of criteria from Table 5 for each alternative. |
| Example: For Time criterion and Pre-Stressed Girder Bridge alternative |
| Weight for Time criterion: 0.0805 |
| Weight of Pre-Stressed Girder Bridge concerning Time criterion: 0.4921 |
| Overall weight of Pre-Stressed Girder Bridge for Time criterion: 0.0805 x 0.4921 = 0.0396. To calculate final weights |
| for each alternative, each alternative weights of all criteria are added. |
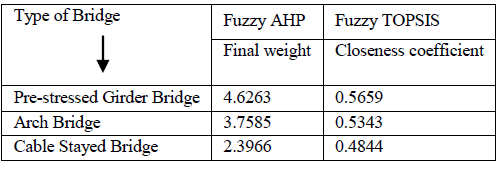
| Final weight of alternative A1- Pre-Stressed Girder Bridge (4.6263) is maximum, followed by A3- Arch Bridge (3.7585) and then A2-Cable Stayed Bridge (2.3966). According to final weights „Pre-Stressed Girder BridgeâÃâ¬ÃŸ is most favourable alternative for the project. |
B. Solution by fuzzy TOPSIS |
| The TOPSIS method was firstly proposed by [21]. The basic concept of this method is that the chosen alternative should have the shortest distance from the positive ideal solution and the farthest distance from negative ideal solution. Positive ideal solution is a solution that maximizes the benefit criteria and minimizes cost criteria, whereas the negative ideal solution maximizes the cost criteria and minimizes the benefit criteria [4]. In this paper fuzzy TOPSIS method is also proposed for the selection problem of type of bridge. Initially, the six decision-makers evaluated the importance of criteria by using the linguistic variables in Table 6. The stepwise analysis of fuzzy TOPSIS algorithm with the help of the case study is explained in the following sections. |
| Step 1: Evaluation of criteria |
| After the identification of criteria and development of alternatives, evaluation of criteria and alternatives is done by the selected panel of experts. Experts are asked to give opinions in the form of verbal judgments. Based on the type of evaluation, verbal judgments are developed for the study. Fuzzy sets used here are taken from [4]. Verbal judgments from different experts are going to be used as an input for the TOPSIS algorithm. Questioners are filled from them through direct communication with them. |
 |
| Step 2: Aggregation of weights |
| Group evaluation is made by aggregating each expertâÃâ¬ÃŸs opinion into one. For fuzzy TOPSIS weights and ratings given by expert panel are aggregated by using Max-Min method by following formula |
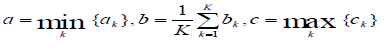 |
| Here, |
| a= minimum value in the set |
| b= mean value in the set |
| c= maximum value in the set |
| k = no. of experts |
| Aggregated weights and ratings are shown in Table 7. |
| Example: For Criteria Time (C1) |
 |
| Aggregation of weights of criteria by Max-Min method |
| In this case: |
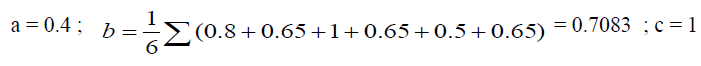 |
| So the aggregated set will be (0.4, 0.7083, 1), displayed in Table 8. Aggregation of ratings of alternatives is done in same manner. |
| Step 3: Construct the fuzzy decision matrix |
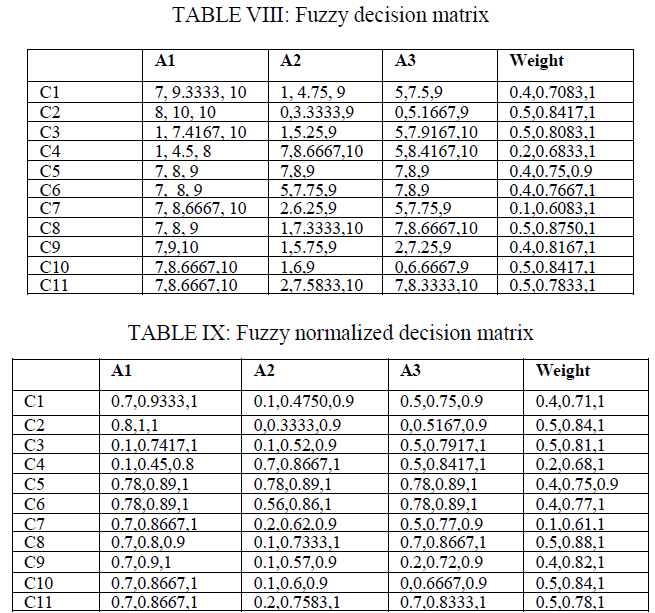
| Aggregation of weights for all criteria is completed by following same procedure described in step 2 and results are given under „WeightâÃâ¬ÃŸ column of Table 8. Aggregation of ratings of all alternative A1, A2 and A3 are obtained for each criterion by following same procedure described in step 2 and results and are given under column A1, A2 and A3 of Table 8. |
| Step 4: Construct the fuzzy normalized decision matrix |
| Construction of fuzzy decision matrix is followed by normalization of ratings. |
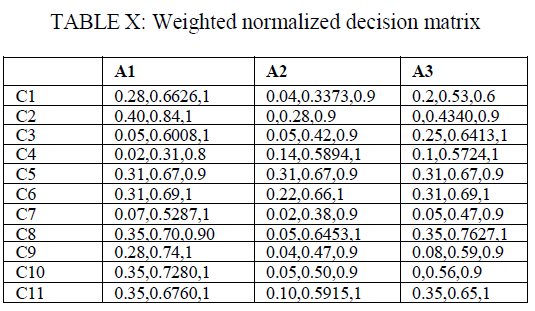
| For fuzzy TOPSIS algorithm the linear scale transformation is used for the process of normalization wherein every element in each row is divided by highest element in the row. In the normalization by linear scale transformation, every element in each row is divided by highest element in the row. For example for row C1 in table highest value is „10âÃâ¬ÃŸ, so every rating of each alternative is divided by „10âÃâ¬ÃŸ. Normalized ratings of all alternatives are shown in Table 9 which represents the fuzzy normalized decision matrix. |
 |
| Step 5: Construct the fuzzy weighted normalized decision matrix |
| After formation of fuzzy normalized decision matrix ratings of alternatives and weights of criteria are combined to construct fuzzy weighted normalized decision matrix. To construct this matrix each set of rating is multiplied by set of weight in same row. |
| For example for row C1 and for alternative A1 in Table 9 |
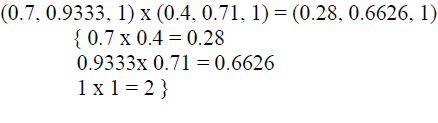 |
| Step 6: Determining FPIS and FNIS |
| After the formation of decision matrix Fuzzy positive ideal solution (FPIS) values and Fuzzy negative ideal solution (FPNS) values are developed which are the two extreme values on the scale of our judgment. FPIS values are found out by developing set of highest element in each row. For example for row C1 in Table 10, highest element in all set is „1âÃâ¬ÃŸ, so FPIS set for criteria C1 is (1,1,1), as shown below. FPNS values are found out by developing set of lowest element in each row from table 10. By following same procedure FPIS and FPNS sets for all criteriaâÃâ¬ÃŸs are developed. |
 |
| FPIS d* {(1,1,1) (1,1,1) (1,1,1) (1,1,1) (0.9,0.9,0.9) (1,1,1) (1,1,1) (1,1,1) (1,1,1) (1,1,1) (1,1,1)} |
| FPNS d- {(0.04,0.04,0.04) (0,0,0) (0.05,0.05,0.05) (0.02,0.02,0.02) (0.31,0.31,0.31) (0.22,0.22,0.22) (0.02,0.02,0.02) (0.05,0.05,0.05) (0.04,0.04,0.04) (0,0,0) (0.10,0.10,0.10)} |
| After developing the FPIS and FPNS for the scale of judgment, the distance of each alternative from FPIS (d*) and FPNS (d-) is found out by vertex method as shown below. |
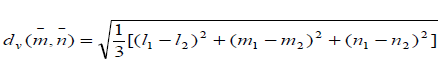 |
| Where, l1, m1, u1 = Values from FPIS and FPNS set for particular row |
| l2, m2, u2 = Corresponding values from Table 10 for particular row |
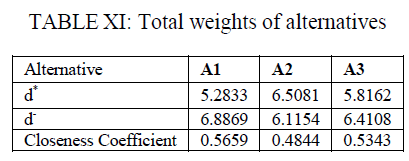
| After calculating distance of each alternative from d* and d-, total weight of each alternative is calculated. Total weight of each alternatives with respect to FPIS (d*) and total weight of each alternatives with respect to FPNS (d-) is to be calculated by adding all distances for each alternative. |
| Step 10: Determining Closeness Coefficient (CC) |
| A closeness coefficient (CCi) is defined to rank all possible alternatives which represents the distance of particular alternative to the fuzzy positive ideal solution (A*) and fuzzy negative ideal solution (A-) simultaneously. Higher closeness coefficient represents particular alternative is closer to FPIS and away from FPNS. The closeness coefficient of each alternative is calculated as |
| The closeness coefficients for the alternatives are given in Table 11. |
` |
| Step 11: Ranking of Alternatives |
| According to the closeness coefficients in Table 11 for three alternatives, the ranking order of three alternatives is determined as A1 >A3 > A2 i.e. pre-stressed girder bridge, arch bridge, cable stayed bridge. The first alternative is closer to the FPIS and farther from the FNIS. According to the results „pre-stressed girder bridgeâÃâ¬ÃŸ is the most favourable alternative for the project. |
OBSERVATIONS & CONCLUSIONS |
| From the study, it was found that both methods suggested pre-stressed girder bridge as the first alternative with highest final weight with fuzzy AHP and highest closeness coefficient with fuzzy TOPSIS. Second alternative given by these methods is arch bridge and cable stayed bridge as the third alternative (Table 12). |
| TABLE XII: Comparison of results of Fuzzy AHP and Fuzzy TOPSIS |
 |
| During the analysis it is found that both methods have some advantages and limitations for the problem which are summarized below. |
| In terms of calculation, fuzzy AHP requires more complex calculations then fuzzy TOPSIS. |
| Fuzzy AHP uses pair wise computations for the evaluation of problem, whereas no pair wise computations is used in fuzzy TOPSIS. |
| In fuzzy AHP framework as the number of criteria increases, the pair wise comparisons become more cumbersome to handle and there is increased risk of inconsistency generation. |
| In fuzzy AHP output, final weights of criteria and alternatives can be equal or zero and this condition is not practically acceptable. |
| In the fuzzy AHP, in some cases if two criterions are of different nature, then it gets difficult to make comparison between them e.g. it is difficult to compare criteria like safety and environmental impact. |
| In fuzzy AHP, difficulty may arise while comparing alternatives, if concerning criteria is does not have direct impact on decision problem. |
| In Indian scenario, use of these advanced techniques along with the conventional methods will be capable of handling complex decision problems and enhance the decision making process. |
References |
|