ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| R.Ramya, K.Selvi, S.S.Nivethitha Department of Electrical and Electronics Engineering, Thiagarajar College of Engineering, Madurai, Tamil Nadu, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper, the Power System Stabilizer is designed using LQR and Robust H∞ loop shaping technique in order to maintain the stability of the system. The weighting function of Robust H∞ loop shaping technique is determined using Genetic Algorithm. The main objective of this paper is to achieve desired stability and analyze the robustness of the centralized controller for multi-machine system and the comparison is made between the LQR based PSS and Robust controller. The LQR based PSS is tested even under perturbations. The suitability of the proposed approach for PSS proves the robustness of the proposed design
Keywords |
| LQR, Robust H∞ loop shaping, Robust controller, Power System Stabilizer, damping; |
NOMENCLATURE |
 |
INTRODUCTION |
| The main objective of installing power system stabilizer (PSS) is to achieve desired stability and security at a reasonable cost by adding damping to electromechanical oscillations. They were developed to extend stability limits by modulating the generator excitation to provide additional damping to the oscillations of synchronous machine rotors. In recent years there has been an increasing interest on applying advanced control designs in power systems like adaptive control, H∞ control, μ synthesis, nonlinear control, feedback linearization, fuzzy logic control and neural control. The goal of these studies is to achieve stability and performance robustness. |
| In [1] PSS has been developed based on a reasonable area model, which consist of component models, models of component controllers, and area grid models. A new structure for stability-enhancing excitation controllers designed using a nonlinear multi-machine system model and Lyapunov direct method has been described in [2]. An analytical method so called minimum phase control loop and intelligent method using a Genetic Algorithm (GA) has been proposed in [3] for an offline Power System Stabilizer (PSS). The application of wave variable method in reducing the effect of delay during the transmission of control signals via large distances in a multi-machine power system has been introduced in [4]. In [5] a systematic approach to damp the low frequency oscillations is observed in Three Machine Nine Bus Multi-machine Power Systems based on Genetic Algorithm (GA). The Optimal Controller design problem is formulated as an optimization criterion comprising of Time domain based objective function to compute the optimal controller parameters. In [6] the proposed RPSS is free from common deficiencies at normal power system nonlinear controllers which are network dependent and equilibrium dependent. In [7] PSS have been designed using Glover– McFarlane H∞ loop-shaping technique for multimachine system based on sequential tuning. |
| In this paper, the PSS has been developed using various methods such as LQR and Robust control design. A new thing in this paper is application of Optimization algorithm (Genetic Algorithm) to determine the weights in designing Robust PSS. Generally optimization technique is applied in designing robust PSS to determine the parameters of PSS only, but here it is applied to determine weights in designing Robust PSS. Conventional stabilizers are not designed in a way to guarantee the desired level of robustness. Such designs are specific for a given operating point; they do not guarantee robustness for a wide range of operating conditions. The resulting LQR-PSS and Robust H∞ loop shaping procedure based PSS ensures the stability for a set of operating points with respect to the nominal system and has good oscillation damping ability. The LQR based PSS is tested even under perturbed condition such as change in mechanical torque. |
PROBLEM DESCRIPTION |
| In Fig 1, Generators gen1 and gen2 are local generators and the rest of the system is approximated by infinite bus system. The two generators are of different ratings, one with 920.35MVA, 18KV, 60Hz and the other with 911MVA, 26KV, 60Hz units. In simulation studies, each of these two generators will be represented by a transient model. With an infinite bus in the network, its voltage phasor can be conveniently chosen as the reference phasor for the angle of other bus voltages and rotor angles. If there is no infinite bus, the rotor q-axis of one of the generators may be chosen as the reference axis instead. In a simulation, the rotor speed of the reference machine can be held steady by setting its inertia to some very large value. The PSS is designed for two generator infinite bus system using various techniques such as LQR and GA tuned robust controller. |
 |
| where Ks is termed the synchronizing torque coefficient. In the Laplace domain, the above differential equation becomes |
 |
| critical and may be in the range of 1 to 20 seconds [11]. The main consideration is that it is long enough to pass stabilizing signals at the frequencies of interest unchanged, but not so long that it leads to undesirable generator voltage excursions during system islanding conditions. The stabilizer gain KS determines the amount of damping introduced by the PSS. Ideally, the gain should be set at a value corresponding to maximum damping. Since the purpose of a PSS is to introduce a damping torque component, a logical signal is to use for controlling generator excitation is the speed deviation Δωr. |
LINEAR QUADRATIC REGULATOR |
 |
 |
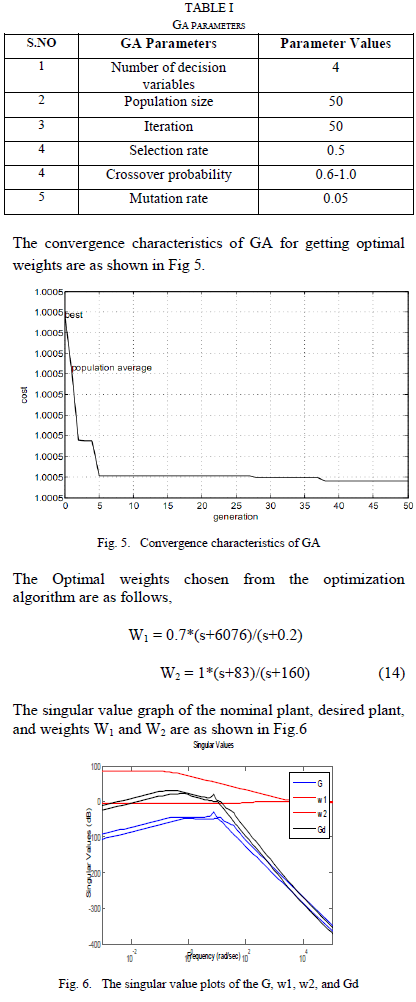 |
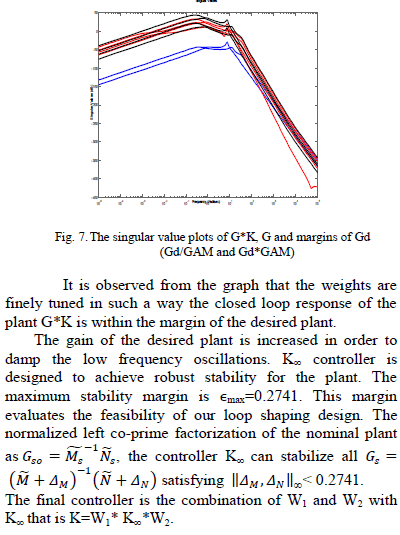 |
SIMULATION RESULTS |
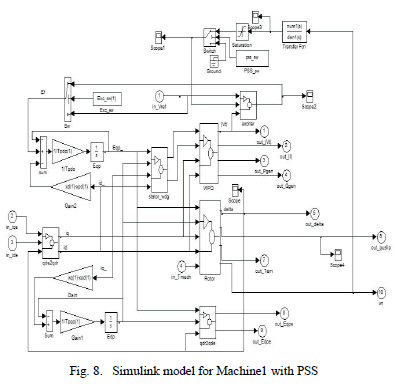
| The Simulink model for Two Machine Infinite bus system is developed. The model for Machine1 with PSS is shown in Fig.7. The mechanical and electrical equations of generator are modeled inside the rotor and stator_wdg block. In this model, the transformations of the input stator abc voltages to the rotor qd reference frame are performed inside the qde to qdr block. The transformation uses the cosθr(t) and sinθr(t) generated by the oscillator block. The VIPQ block is generated in which the instantaneous magnitude of the stator voltage, stator current, and stator real and reactive power at the generatorâÃâ¬ÃŸs terminal are computed. The instantaneous values of the real and reactive power in per unit flowing out of the stator terminals of the generator are computed from the following equations: |
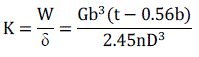 |
 |
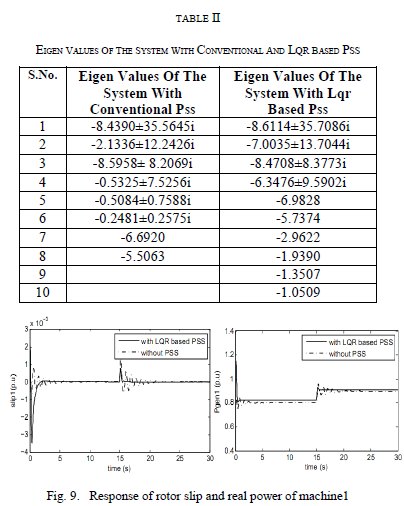
| The stability condition of the system can be examined using their eigen values. Hence the system eigen values are determined and listed in Table 2. In Table 2, first column shows the eigen values of the system with the presence of conventional Power System Stabilizer and second column shows the eigen values for the system with the presence of PSS modeled based on LQR technique. From the table, it proves that the oscillations are reduced in the system using LQR based PSS since four oscillatory eigen values are damped out completely and also some of the eigen values moves to the large negative value. It shows that the system moves towards the stability region quickly while using LQR technique. |
 |
 |
| Simulation is done for three different cases: (i) System without PSS, (ii) System with LQR based PSS and case (iii) System with Robust PSS. All parameters of the system are analyzed after the simulation is carried out. |
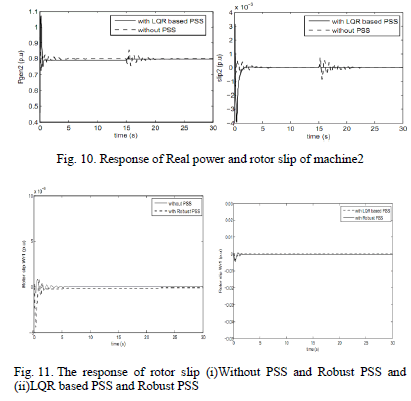
| Among that, the response of rotor slip and real power of both machines are shown in Fig.8 and Fig.9. In these Figures, comparison is made between two cases: system without PSS and system with LQR based PSS. The analysis is made with the Tmech disturbances i.e., the magnitude of Tmech is changed from 0.8 p.u to 0.9 p.u.at time t=15s. So at this instant, there are some oscillations present in the system. But with the use of LQR based PSS, the oscillations are damped out quickly which proves in the fig.8 and Fig.9. Hence it is observed that the LQR based PSS damps out the oscillation well even under perturbations. |
| Comparison is also made between LQR based PSS and Robust PSS which shown in Fig.10. The response of the rotor slip of machine1 without PSS and with Robust PSS is as shown in first Fig.10. It is observed from the above graph that the response of rotor slip in machine1 with Robust PSS has faster response compared to that of the system without PSS. In case of comparison with the LQR based PSS it is observed that there is only slight difference in damping out oscillations. All the remaining electrical parameters such as Voltage, Current, Reactive Power, Torque and angular speed are also analyzed for all the three cases. |
CONCLUSION |
| A systematic approach to design PSS using LQR technique and Hinf loop shaping procedure is presented for two generator infinite bus system. The analysis is made to verify the robustness of the designed controller using loop shaping procedure. Genetic Algorithm is applied to determine the weights while designing robust controller. The resulting PSS can stabilize the nominal plant. Proposed work demonstrates the good damping performance of the designed controller and the comparison is made between LQR based PSS and Robust PSS. The LQR based PSS is tested under perturbations such as change in mechanical torque and found to have better damping performance even under perturbation. The above procedure can be applied to large multi-machine to design the robust controller to take care of the oscillations under perturbed conditions. |
ACKNOWLEDGMENT |
| The authors are thankful to the Management of Thiagarajar College of Engineering, Madurai for providing required facilities. |
References |
|