ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
M.C.Jobin Christ1,Ramanan Subramanian2, R.Thirumalvalavan2,A.Vignesh2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The brain tumors are the mass of undifferentiated cells which undergoes uncontrolled proliferation of cells in the brain. Segmentation of these tumors is more difficult than natural. Because their functional sensitivity is higher than other images. Many different algorithms have been proposed for segmentation of these type of tumors in brain images. In this paper, we propose an approach in order to improve efficiency of the brain tumor segmentation through the minimax optimization that applies to the thresholding of the MRI brain image to segment tumor. The tumor segmentation is performed by the implementation of an optimistic technique called variational minimax optimization. The proposed system uses search of optimum threshold with an iterative line search technique with faster execution time of 15 seconds.
Keywords |
| Line search Optimization,Minimax, Optimum,Segmentation, Tumor detection. |
INTRODUCTION |
| The tumors are the growth of cells which are abnormal in their nature that may differ from the normal cells by their uncontrolled characteristics of the tissue growth factors, growth periods. The tumors are easily identifiable in the radiological images such as X-rays, MR images and CT scan images. As the tumors are highly denser than normal cells, they are specific to its identification. There are many methods involved in the brain tumor image segmentation. Mostly the existed methods use the normalization and use of preprocessing techniques. The specificity of the tumors are very comfortable in images for segmentation. |
II. LITERATURE SURVEY |
| The tumor detection and segmentation in the previous system include the use of the clustering techniques like SOM, Fuzzy C means and using machine learning algorithm. After the usage of these techniques, certain optimization techniques are determined. These techniques include swarm intelligence approach, hybrid technique involving the genetic algorithms, colony optimizations.K means is a technique which is a unsupervised segmentation method doesnot requires considerable amount of training and testing data and comparatively doesnot complicates the process[1]. This method can be applied to the minimal amount of data with reliable results.[2] In Fuzzy C means method of image segmentation, the fuzzy logic is a way to processing the data by giving the partial membership value to each pixel in the image[3]. The membership value of the fuzzy set is ranges from 0 to 1. Particle Swarm Optimization is a new technique that uses the initialization of certain particles along with velocity to move[4].The particles are moved in a random direction. The position of particles and velocities are updated. PSO has been used to produce a new optimization-based image segmentation method[5].In order to find a proper threshold value with a high efficiency, ant colony algorithm is used. In this method, pixels of the image are assumed as food for ants[6]. Then ants deposit their pheromone on the pixels which is effective on other ants’ movement. Artificial Bee Colony (ABC) is a novel optimization algorithm inspired of the natural behaviour of honey bees in their search process for the best food sources.[7]This algorithm do not guarantee high accuracy especially for noisy or abnormal images. |
III. METHODOLOGY |
| The proposed energy functional consists of a data term and a regularization term [8]. The data term encourages the threshold surface to intersect the image surface at high gradient location and the regularization term imposes smoothness on the threshold surface. The first component of the energy functional dictates the threshold surface to intersect the image surface at high gradient places and the second component of the energy functional is responsible for smoothing the threshold surface.In order to find out the solution, i.e., the desired threshold surface, we propose a variational minimax (VM) optimization. The VM algorithm consists of two interleaved iterative steps: maximization with respect to the weighting parameter and variational minimization with respect to the threshold surface[9]. VM method avoids multiple minimization computations by virtue of a deliberate choice of concavo-convex energy functional. The proposed method consists of the image function “I” and the threshold function “T”. The energy function in the proposed system can be given as |
 |
| 1. The first step of the algorithm is to get the image from the database. In our system, we have used the MR brain image database to acquire brain image. 2. The image is normalized to map linearly with the range (0,1). 3. Compute the gradient of the image. 4. The threshold surface is initialized. 5. Compute the alpha for determination of optimal function using formula, 6. The line search optimization is performed by using heat equation updating with respect to time and iteration. (1-(α*)2h(I-T))1/2. |
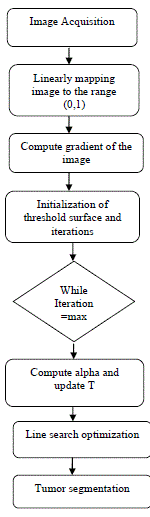 |
| Fig.1 Flow Chart |
IV. IMPLEMENTATION |
| The algorithm is used in the image processing for the segmentation of tumor. It is implemented in the MATLAB R2009a version with a computer system of dual core processor. The iterations for line search optimization[10] involves the following steps. Step1:Determine a direction of search Step2:Find time by minimizing E. |
| Step3:Set T(k+1) = T(k) +τ(k)δT(k) . |
| The line search step, i.e., Step b is fast: we increase τ(k) starting from ¼, so long as the expression e1 + τ(k) e2 + (τ(k))2 e3 decreases. After the line search optimization, variational minimax algorithm undergoes the iterations to give the optimum value of alpha for tumor segmentation. |
V. EXPERIMENTAL RESULTS |
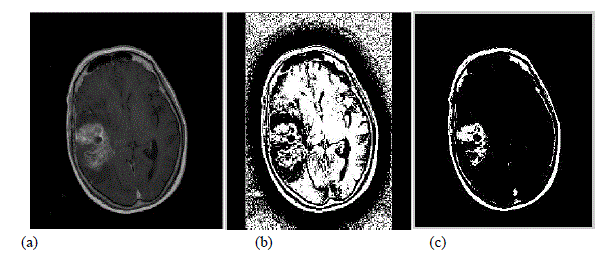 |
| Fig. 2.Experimental Results (a) Original Tumor image 1 (b) Image during line search optimization (c) Result of Optimization |
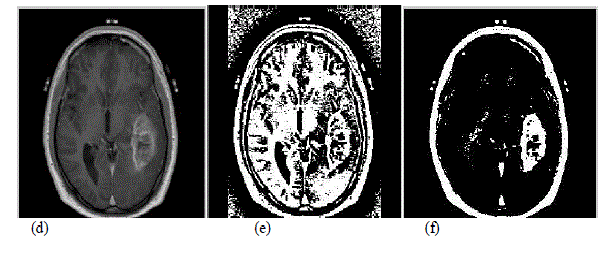 |
| Fig.3 Experimental Results (d) Original Tumor image2 (e) Image during line search optimization (f) Result of optimization |
| The above figures represent the experimental results obtained by applying the proposed system in the MR brain images. The figure (a) and (d) are the input images from the database. The images (b) and (e) are obtained by applying variational minimax technique during line search optimization. The images (c) and (f) represent the result of the implementation of the proposed system for the brain tumor segmentation. The optimum value alpha obtained in the result is shown in figure as follows. For tumor image 1, alpha value obtained is 0.68. While for tumor image 2, alpha value obtained is 0.587. The segmentation of the tumor by our proposed system executes the result within the time period of 10-20 seconds with great accuracy. |
 |
| Fig.4 (a) Screenshot of alpha value for tumor image 1 (b) Screenshot of alpha value for tumor image 2 Area Calculation is made by the simple calculation of knowing the properties of image.[11] Mostly the image has 256*256 pixels Area of an image is the total number of the pixels present in the area which can be calculated in the length units by multiplying the number of pixels with the dimension of one pixel. Image, I = Σ 255ïÿýïÿý=0Σ 255ïÿýïÿý=0[f(0) + f(1)] (9) Pixels = Width (W) X Height (H) = 256 X 256 f (0) = white pixel (digit 0) f (l) = black pixel (digit 1) No_ of_ white pixel P = Σ 255ïÿýïÿý=0Σ 255ïÿýïÿý=0[f(0)] (10) Where, P = number of white pixels (width*height) |
VI. CONCLUSION |
| We have implemented an automatic brain tumor segmentation technique . The algorithm successfully detects the tumor region. We have applied this algorithm on many images and found that it successfully detect the tumor with better accuracy of result with lesser execution time. |
References |
|