Research and Reviews - International Journals

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Automatic Melanoma Detection Using Multi- Stage Neural Networks

Nikhil Cheerla1, Debbie Frazier2
  1. Student, Monta Vista High School, Cupertino, CA, USA
  2. Teacher, Computer Science and Biology, Monta Vista High School, Cupertino, CA, USA
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Skin cancer accounts for more than half of all cancers detected in USA every year. Melanoma is less common, but more aggressive and hence more dangerous than the other types of skin cancers. Even though there has been extensive research in the past 20 years on automatic melanoma detection from skin lesion images, most of the dermatologists still do not have access to this technology. In this paper, a novel system is proposed. The system uses enhanced image processing to segment the images without manual intervention. From the segmented image, it extracts a comprehensive set of features using new and improved techniques. The features were fed automatically to a multistage neural network classifier which achieved greater than 97% sensitivity and greater than 93% specificity. The trained system was tested with lesion images found online and it was able to achieve similar sensitivity. Finally, a new approach that will simplify the entire diagnosis process is discussed. This approach uses Dermlite® DL1 dermatoscope that can be attached to the iPhone. After taking the lesion image with a dermatoscope attached iPhone, the physician gets the diagnosis with a few simple clicks. This system could have widespread ramifications on melanoma diagnosis. It achieves higher sensitivity than previous research and provides an easy to use iPhone based app to detect melanoma in early stages without the need for biopsy.

Keywords
Neural networks, Melanoma, Image Processing, Dermatoscope, Classifiers, iPhone

INTRODUCTION
Skin cancer is by far the most common cancer in United States. Melanoma accounts for less than 5% of all skin cancers but causes a majority of the skin cancer deaths. Initial diagnosis of Melanoma is done by visual inspection of the skin lesion for distinct features. Friedman et al. [7] proposed a set of accepted features that all Melanoma lesions, to some extent, contain. These features are expressed using a simple mnemonic - “ABCD”. These letters stand for Asymmetry, Border Irregularity, Color Variation, and Diameter. Abbasi et al. [1] enhanced this mnemonic to add the letter „E‟ which stands for evolution. Dermatologists predominantly use these features to classify lesions visually and to determine whether they need further invasive techniques to diagnose malignancy. In recent years, there has been a surge in computer aided, non invasive diagnosis tools for various cancers that were widely embraced by the experts. Even though skin cancer is very pervasive, the diagnosis is still based on visual inspection and biopsy. This is perhaps due to the difficulty in achieving the acceptable sensitivities and specificities using skin images. An automatic classification system, which can accurately classify skin lesions with sensitivity comparable to an expert, would increase the chances of early diagnosis and treatment and decrease the fatality rate of melanoma. The classifier also helps reduce the unnecessary biopsies conducted based on visual classification. Furthermore, if the classification system uses machine learning and artificial intelligence techniques, its accuracy can increase as it encounters more examples of lesions. If the classifier could be made widely available to the physician community, it has the potential to reach even higher levels of sensitivity and specificity and can classify the images better than expert dermatologists. There are a considerable number of studies on automatic melanoma detection. Celebi et al. [4] summarized all the reseach in this field in the past 30 years and provided future guidance for medical image analysis. Most research in this vein revolves around analysis of skin lesion images taken using dermatoscope (dermoscopic images) and falls under three different categories: mathematical modeling based on certain features of the lesion, fuzzy-logic based systems, and neural network based systems.
Stoeker et al. [20] proposed an automated classifier that quantified certain features of the lesions and applied it to a formula. If the result of the formula is above a certain threshhold, the lesion was classified as malignant. Otherwise, the lesion was classified as benign. Although this formulaic approach was able to achieve a sensitivity of above 80%, this system had no way of learning from experience with new lesions and thus is inferior to even a standard visual inspection. Stanley et al. [17] proposed a fuzzy logic based color histogram analysis technique for skin lesion determination. However, significant color changes in melanoma skin lesions occur only in advanced stages. Depending entirely on the color histogram alone will not help in early detection [6]. Fuzzy classification techniques also have the tendency to over-fit due to the absence of learning. Since fuzzy logic uses more advanced techniques to detect lesions, it is certainly preferable to a simple formula. However, unlike a machine learning based system, the accuracy of the system does not improve after the initial system parameters are chosen. Neural networks can be thought of as continuously evolving function approximators. Since they can provide a concrete rule to analyse images, and yet learn to modify the rules from experience, they are clearly superior to fuzzy logic and automatic systems. Ercal et al. [6] described a basic neural network classifier that extracts the asymmetry, border irregularity and color features of an image and fed them to a feed forward neural network. However, due to the limited number of features extracted, the system could only achieve between 70-80% classification accuracy. Jaleel and Saleem [10] described a neural network based classifier that did not use any of the ABCD features but relied on features extracted from the 2-D wavelet transformation of the images. The sample size used in their classification was small (less than 21 images) and there was no mention of the performance or sensitivity achieved by the system. Smaller training and testing sample sizes usually lead to over-fitting, in which the learning system tends to adjust to specific random quirks of the training data that cannot be generalized to larger samples. Gniadecka, et al. [9] proposed a technique that used Raman spectroscopy and neural networks for detecting skin cancers. They targeted a laser beam at the skin lesion to excite the molecules in the lesion. The scattering effect of the molecules in the skin lesion causes frequency shifts in the reflected Raman spectra. They trained a neural network with the reflected beam‟s frequency characteristics, and were able to get good sensitivities. However, Raman spectrometers are not widely available and are very expensive, and hence are rarely used by dermatologists. Although much work has been done in the field of neural network based classification of dermoscopic images, there is yet to be a classifier that is accurate, practical, and general enough to have a real-world impact.

II. OBJECTIVES
There were significant shortcomings in the previous research on melanoma detection from dermoscopic images. Firstly, the image segmentation was not completely automatic. Pre-processing and inspection of the segmented image was done manually [13, 18]. Many of these systems did not use a comprehensive set of features, or extracted the features in a way that allowed for little precision [6, 10]. They mainly used single-stage neural network architectures and did not explore the possibility of improving the classification results with different architectures [6, 9, 10]. Finally, there is no widely available software application or diagnosis tool developed using the previous research. Our research aims to overcome these shortfalls. Our objectives are 1. Automate the image segmentation. 2. Improve the scope and accuracy of feature extraction techniques. 3. Create a comprehensive library of features that can be used to summarize the image. 4. Improve the performance of neural networks classification using novel multi-stage architectures. 5. Create an easy to use system/application that detects melanoma with a few simple steps. 6. Make the system widely available to physicians and dermatologists.

III. NEURAL NETWORKS AS CLASSIFIERS
Dermatologists diagnose malignancy in skin lesions based on their extensive training, experience from previous diagnoses, and their access to vast amounts of medical research. Their diagnosis is based on looking at a set of features holistically, since a single feature alone cannot determine malignancy in the lesion. Experience and training-based learning is similarly an important characteristic of neural networks that makes it ideal for diagnosis applications. With advances in processing power and cloud computing resources, there has been a recent surge in using neural networks for medical diagnosis. Neural network, often referred to as Artificial Neural Network (ANN) is a computing system made up of processing elements called neurons which process the information by their dynamic state response to external inputs. Neural networks are typically organized as layers – one input layer, one or more hidden layers and an output layer. Hidden layers are made up of a number of neurons, which contain an „activation function‟. Features/patterns are given to the network via the input layer, which are connected to one or more of the hidden layers. The actual processing is done in the hidden layers through a system of weighted connections. The hidden layers are connected to the output layer. The output layer provides the outcome of the processing or classification [27]. Most neural networks contain some kind of learning function, which modifies the weights of the connections according to the training pattern presented to it. Neural networks learn to classify by examples; the individual neurons are trained with patterns, which is very similar to how the human brain learns to classify. This aspect of the neural networks makes it an ideal system for medical diagnosis, where learning to recognize patterns is the key to accurate diagnosis. A feed-forward neural network with back-propagation is widely used for pattern recognition and classification [27]. In a feed forward neural network, each layer of the neural network is connected to the next layer. „Back-propagation‟ is a type of supervised training, where the network is provided with both the training inputs and the corresponding expected outputs. Using the expected output, the back-propagation training algorithm adjusts the weights of the connections backwards from output layer to the input layer. Since the nature of the error is not known, neural network training needs a large number of individual runs to determine the best possible solution. Once the neural network is trained to a satisfactory level, it is ready to be used as classification tool for new input datasets with unknown classification. During the classification mode, the user does not need to train the network anymore and it acts essentially as a function approximation: it functions to predict the output from the input fed to it. The overall performance of a neural network classifier is defined as the percentage of total inputs (in both training and testing) that are correctly classified.

IV. METHODS
Our method for detecting melanoma lesions involves three steps: lesion segmentation of dermoscopic image, feature extraction, and neural-network based classification. Dermoscopy is the capturing and examination of the skin images using a dermatoscope. A dermatoscope uses special filters that allow viewing and capturing of the skin lesion without obstruction by the reflection from other skin surfaces. Even though there were some smart phone applications that claim to diagnose melanoma and other types of skin cancers with regular digital images, melanoma cannot be detected with reasonable accuracy with digital images taken by DSLR, point and shoot or smart phone cameras since the image quality and lighting is poor [21]. For this project, the dermoscopy images database from Computational Vision Laboratory at the Department of Electrical Engineering of the Universidad de Chile were used [16]. The images in this database were obtained at the Dermatology Service of Hospital Pedro Hispano (Portugal) under the same conditions through a dermatoscope. They are 8-bit RGB color images with a resolution of 768x560 pixels. The database (referred to as PH2 database in this paper) has 200 pre-classified images containing 40 melanoma and the rest non-melanoma images. However, many of the images in the database were not usable as the lesions were not fully contained inside the image. Using a partial lesion could lead to wrong diagnosis. The partial lesions were later discarded by our image segmentation algorithm. MATLAB software was used to perform image processing and neural network architecture design and training.

V. IMAGE SEGMENTATION
In skin lesion segmentation, the noise, like hair and uneven pigmentation is removed from the image and the skin lesion is segmented from the surrounding skin. There has been extensive research in image segmentation. Nammalwar et al. [13] discussed a technique that segments the skin lesion using the color and texture differences between the lesions and surrounding skin. They used a modified K-means algorithm for color segmentation [22] and local binary pattern (LBP) changes for texture segmentation [23]. However, from the limited samples (less than 20) used in the analysis, the segmented lesion images seemed to have included a significant portion of the normal surrounding skin which could lead to incorrect feature extraction. Xu, et al. [18] proposed a technique where initial segmentation is done by converting the image to LAB color format. Then the boundaries were refined using edge detection and gray thresholds. While this technique produced reasonably accurate segmentation results (less than 5% non-overlapping area when compared to manual segmentation results done by 3 different experts in their research), the method is not automatic. The user needed to provide various parameters like Gaussian smoothing parameter, threshold value for initial segmentation and adjust them by trial and error based on the color and texture of each individual image until good segmentation results were obtained. A method to simplify and automate the task of image segmentation was proposed. The final result of lesion segmentation is a black and white mask where all pixels corresponding to the skin lesion are white. This mask can be applied on the original image to mask out all the non-lesion skin areas from the image. This enables all feature extraction steps to only extract features and characteristics from the skin lesion, and not the surrounding skin. In addition, the mask can be used standalone to study the contour of the lesion. Digital images are prone to noise from various sources. The image acquisition process as well as electronic transmission of the image could introduce noise – this results in pixel values that do not represent the true intensities of the image. A Gaussian filter was used on the image to reduce the noise. A Gaussian filter is a low pass filter that suppresses high frequency detail while preserving the low frequency components of the image. A sigma value of 0.5 was chosen to enable noise filtering while still keeping the edge components of the image. After filtering, a well-known technique called „dull razor‟ [11] was used to remove the hair from the image. After Gaussian filtering and hair removal, Red (R), Green (G) and Blue (B) components as well as the Saturation (S) and Intensity (I) components of the image were extracted. Each component was converted into its corresponding black and white representation using its respective gray threshold determined by Otsu‟s method available in MATLAB [14]. Otsu‟s algorithm assumes that the image to be classified contains two classes of pixels. It finds the optimal threshold that differentiates these two classes of pixels such that variance is minimal within each class. A final black and white image is obtained by merging all the black and white images obtained in the previous step. In this image, the lesion pixels are black and the surrounding pixels are white. A morphological closing operation followed by filling the holes was performed on the compliment of the image obtained from the previous step. This operation fills holes inside the mask and creates a mask image where pixels corresponding to the lesion are white and surrounding skin pixels are black. Converting individual R, G, B, S and I components of the image to black and white images, and then merging these images together creates a finer black and white mask which preserves all edge details. As the final step, Canny Edge Detection is applied to the mask to create an image border. Canny Edge Detection detects the edges by finding gradient maxima of a Gaussian smoothed image. This algorithm gives superior results compared to other algorithms for edge detection [3]. Figure 1 shows the images at intermediate steps of the segmentation algorithm.
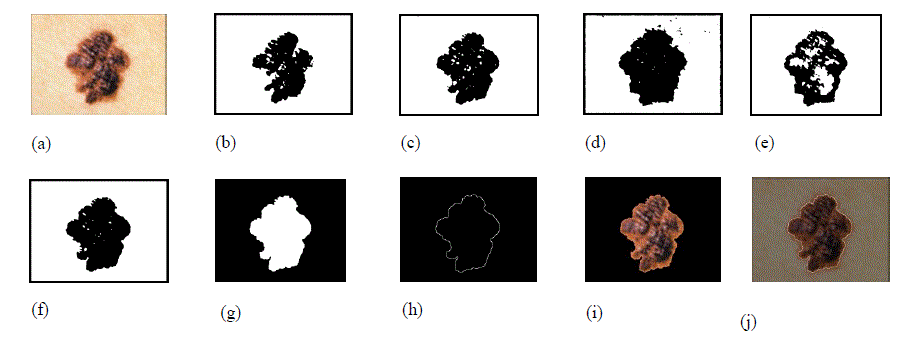image
Figure 1. Image segmentation steps. (a) Original image. (b) Red component of the image converted to black and white using its gray threshold. (c) Green component of the image converted to black and white using its gray threshold. (d) Blue component of the image converted to black and white format using its gray threshold. (e) Saturation component of the image converted to black and white image using its gray threshold. (f) Intensity component of the image converted to black and white image using its gray threshold. (g) Final mask obtained after merging images (b) through (g) and removing small objects, filling the holes and complementing the image. (h) Image border obtained using edge detection. (i) Segmented image without the surrounding skin. (j) Original image with the contour overlapping to show the accuracy of segmentation. Due to freckles and other uneven bumps in the surrounding skin, the mask image could have multiple tiny objects in addition to the mask for the skin lesion. By keeping only the object with the largest area, these tiny granules can be filtered out. If the skin lesion is not completely enclosed within the image, it is automatically detected (by the fact that the mask extends all the way to the border of the image) and the image is marked as a segmentation failure. Figure 2 illustrates a segmentation failure due to the lesion not being fully enclosed in the image. If the contrast between the skin lesion and surrounding skin is not good enough, the Otsu‟s gray threshold algorithm picks up a large chunk of the surrounding skin, extending all the way to the border of the image. This also results in a segmentation failure, as the mask extends all the way to the border of the image. Whenever a segmentation failure is detected, the algorithm enhances the individual components of the image using the adaptive histogram equalization function in MATLAB [24] to improve the contrast between the lesion and the surrounding skin, and applies the segmentation algorithm again. By doing the adaptive histogram equalization, segmentation failures caused by lower contrast between the lesion and surrounding skin get fixed. Figure 3 shows an image which has a segmentation failure in the first pass, but the algorithm was able to detect the lesion after applying adaptive histogram equalization to the image. If there is a segmentation failure after the second pass, the image is discarded.
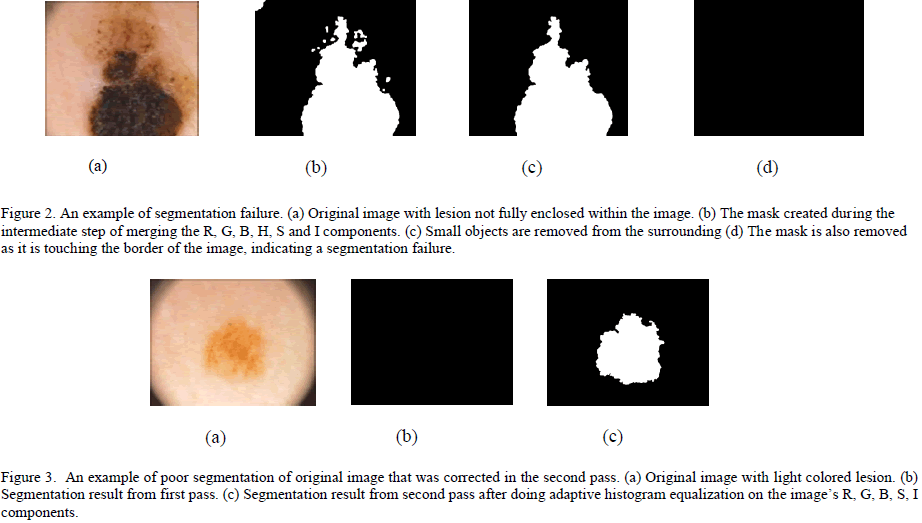image
When the algorithm was applied on 200 images in PH2 database, 11 images were marked as segmentation failures. After manually inspecting these 11 images, it was found that all the failures are due to the lesion not being completely enclosed within the image. In these cases, it is better to discard the image and report a failure since the features extracted from the partial lesion could result in inaccurate diagnosis. If a mobile technology were created, following this segmentation failure, the user would be prompted to acquire a new image. Figure 4 shows the results of segmentation for some sample images in the data set.
image
Out of the 11 segmentation failures, 10 belonged to melanoma images. After discarding those images, there were only 30 usable melanoma images from the PH2 database. For good training, it is essential to have equal representation of both melanoma and non-melanoma images. Hence, 14 additional dermoscopic images of melanoma from various sites [29, 30] were obtained and after randomly selecting 44 non-melanoma images (that segmented successfully) from the PH2 database and a new database of 88 images (with 44 melanoma and 44 non-melanoma images) was created for further analysis.

VI. FEATURE EXTRACTION
For accurate detection of melanoma, it is critical to extract a comprehensive set of features. We extracted information about asymmetry, border irregularity, color and texture from the image. Since each image could have different magnification and scale, finding the „Diameter‟ of the dermoscopic images is not accurate unless all images are normalized. Although the „ABCDE‟ rule states that most of melanoma lesions are > 6mm in diameter, the incidence of small diameter melanomas is on the rise. About 14% of the melanomas detected worldwide are small diameter melanomas [1]. Thus, by excluding the diameter as differentiating feature between melanomas and benign lesions, our system has better chances of detecting small diameter melanoma if the system was able to achieve good sensitivity using rest of the features. The „Evolving‟ nature of the lesion is analysed by comparing the changes in texture, color and diameter of the images over a period of time. Due to the lack of this information in the database, current research was focused on detecting the melanoma from a given image of the lesion itself, and not from multiple images taken over a period of time. A. Asymmetry Asymmetry is a distinct characteristic of melanoma lesions. Ercal et al. [6] used a technique (referred to as Reflection Asymmetry method in this paper) where the image is reflected on to itself over the major axis. The percentage of asymmetry was computed as the ratio of overlapping area (of the image and it‟s reflection over the major axis) to the total area occupied by the image and its reflection. If the image is completely symmetrical, the ratio is 1. As the asymmetry increases, the ratio approaches closer to 0. However, this technique would classify some non-elliptical shaped lesions (like pear shaped skin lesions) as symmetrical even though these shapes are more likely to be melanoma than benign. A new technique, called Elliptical Symmetry method, to complement the Reflection Symmetry method is proposed. This new method fits an ellipse around the image and computes the asymmetry index as the ratio of the area of the non-overlapping region between the ellipse and the image to the total area occupied by the ellipse and the image. For a fully symmetrical and elliptical shaped lesion (including circular shaped lesions – circle is a form of ellipse with equal major and minor axis), this ratio is 1 and decreases towards 0 as the asymmetry increases. Figure 5 illustrates the steps in computing asymmetry for a melanoma image using the Reflection Symmetry method and our Elliptical Symmetry method.
image
Figure 6 shows a plot of asymmetry indices for 88 image database using both Reflection Symmetry and Elliptical Symmetry methods. Both exhibited good correlation to the classification result when a Pearson Correlation was applied. Pearson Correlation coefficient is a measure of linear correlation between two variables. If the correlation coefficient is 0, there is no correlation. A correlation coefficient of 1 indicates a strong positive correlation and a value of -1 indicates a strong negative correlation.
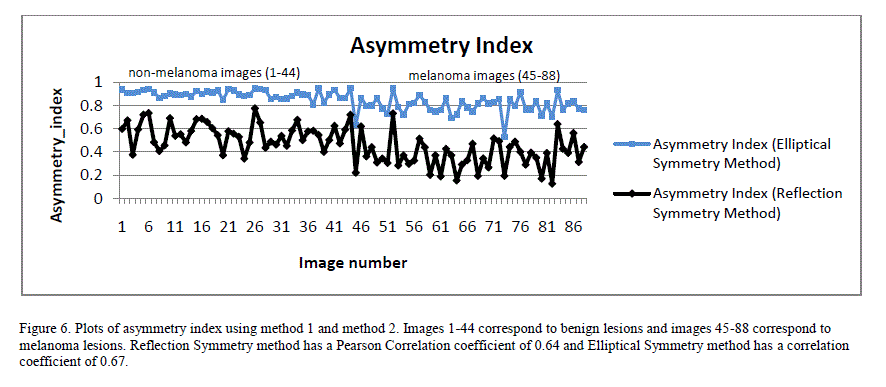image
B. Border Irregularity Malignant skin lesions tend to have irregular borders with sharp edges and notches. Benign lesions tend to have smooth borders. Irregularity index is a function of area (A) and perimeter (P), calculated as 4����/��2 [6]. For a perfect circle, the irregularity index is 1. As the border becomes more irregular, the index reaches 0. Figure 7 shows the plot of the irregularity index of the 88 images in the database using this method (referred to as Method 1). Although this method gives a rough approximation of the irregularity index, it could give false measurements for some shapes. As an example, for a perfect ellipse with major axis half of the minor axis, the index is 0.8 even though the border is smooth.
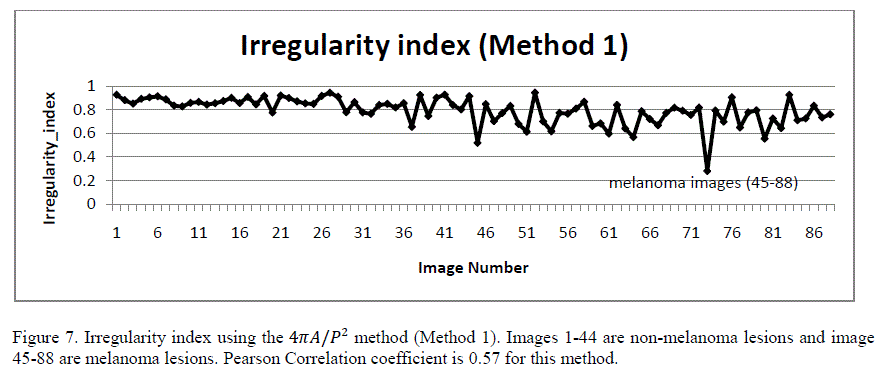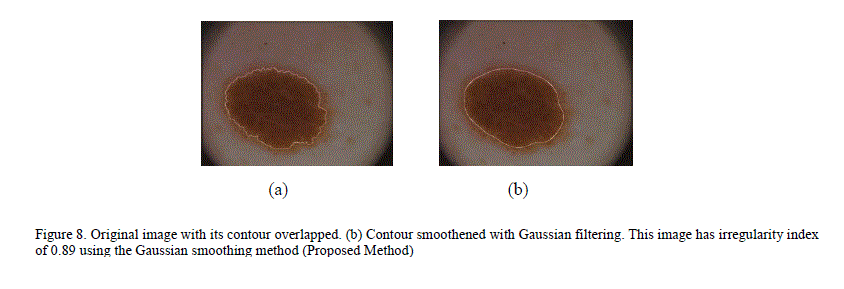
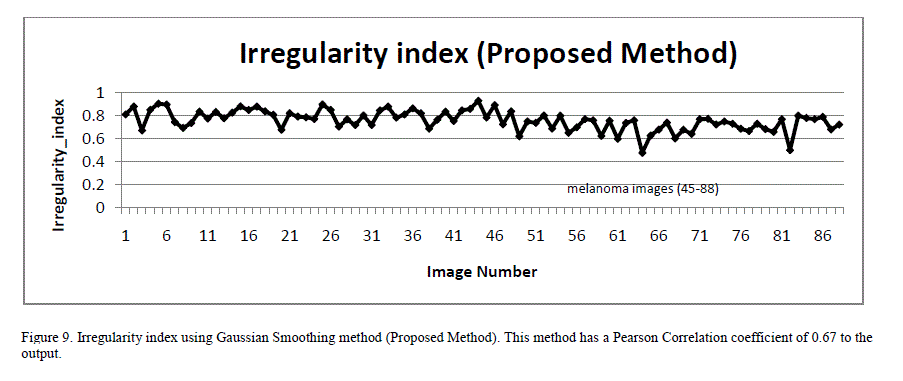
image
To overcome this inaccuracy, a new technique for quantifying irregularity is proposed. In this technique, the lesion mask is smoothed using Gaussian filtering with a Sigma of 16 to remove all sharp edges and notches in the image. The irregularity index is the ratio of the perimeter of the smoothed version of the mask to the perimeter of the original mask. For images with smooth borders, the irregularity index approaches 1. As the border irregularity increases, the index reaches 0. Figure 8 illustrates an image with many sharp corners and how it gets smoothened with Gaussian filtering. Figure 9 shows a plot of the irregularity index using our proposed approach.
image
image
Fractal dimension analysis and box counting techniques were also used widely in previous research as a measure of border irregularity for skin lesions [12]. Lacunarity, similar to fractal dimension, is a mathematical term that can measure rotational invariance and heterogeneity. Patterns which are homogenious have lower lacunarity. Lacunarity analysis is used extensively in texture and border analysis in various fields [15]. However, there is limited research on using lacunarity for melanoma image analysis. Gilmore et al. [8] proposed lacunarity analysis to study the structure of skin lesions by doing the analysis seperately on R, G and B components of the image. Lacunarity analysis was performed only on the border of the image (obtained during image segmentation) to quantify the heterogeneity of the border. Lacunarity of the image border for a box size of „r‟ could be computed by using the below formula, which uses the gliding box algorithm [15] . V(r) is the variance and M(r) is the mean of the number of white pixels in a box size „r‟.
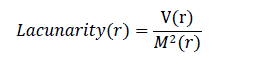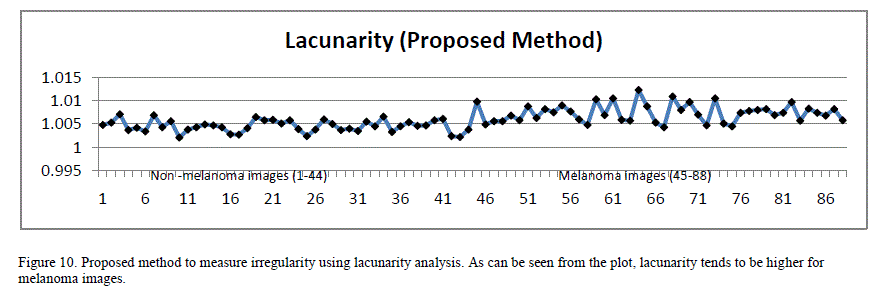
image
Since the images are of different scale and dimensions, in order to perform this analysis, the border images were cropped around their bounding boxes and the resulting images were scaled to 256 x 256 pixels dimension before extracting lacunarity. When the box size is 1, lacunarity indirectly indicates the ratio of white pixels to the black ones in the image. Figure10 plots lacunarity for the images with a box count size of 1. As can be seen from the plot, lacunarity tends to be slightly higher for malignant lesions compared to benign lesions. The lacunarity index exhibited strong Pearson‟s correlation coefficient (0.66) to the classification results.
image
Some melanoma lesions exhibit color variations with a swirl of red, black, brown and light blue components in the lesion. Benign lesions predominantly consist of single color region [7]. Various techniques were used in previous research for extracting color variations from the lesion images. Chen et al. [5] proposed a technique that bins cumulative color histograms of images, and tag each bin as either melanoma, benign, uncertain or unpopulated based on the probability of the melanoma and benign skin lesions occupying that specific bin. They obtained around 83% classification accuracy with a neural network trained using this method. Since this technique used only the color characteristics of the melanoma and did not rely on other features, the accuracy was lower. A novel approach to identify the number of distinct colors in the lesion was proposed. This method extracted 4 most significant colors from the image using the minimum variance quantization function of MATLAB. Then, distance between these colors in RGB space was computed. The distance is compared against a threshold value (T). If the distance between any two colors is greater than the threshold value, they are considered distinct colors. The total number of distinct colors in the image is computed using this algorithm. After trial and error, a threshold value of 0.4 was chosen as it correlated closely with human determination of the number of colors on a sample set. As shown in Figure 11, a high proportion of melanoma lesions do show 2 or more colors, while a very low proportion of benign lesions show more than 1 color. Hence, this characteristic combined with other features can help discriminate melanoma lesions.
image
A. Texture Classification Skin lesion texture could be extracted using various methods. Wavelet transformation based texture analysis had been used widely in image analysis. Wavelet Transform uses waves of limited duration, called mother wavelets to represent a signal. These wavelets are localized in both time and frequency domain. Using coefficients, a signal can be represented as a combination of wavelets of different scales and frequencies originated from the mother wavelet. Many different families of mother wavelets exist. For the current analysis, a Debauche 3 series mother wavelet was used. 2D ( two dimensional) wavelet decomposition does wavelet transformation of the image, and then separates the low scale high frequency wavelet components (referred to as details) and high scale low frequency wavelet components (referred to as approximations). This transformation is used widely to separate the coarse and fine features from an image in image processing. Figure 12 is an example of wavelet decomposition. Here, after doing the wavelet decomposition to separate the approximate and detail components, the image is reconstructed using only the detail component‟s wavelet coefficients. As can be seen from the image, the detail coefficients capture the high frequency components (change in texture, color) of the image. Wavelet decomposition can be iterative, with each of the approximation and detail components further splitting into second level approximation/details components. For wavelet feature extraction, using the MATLAB function, 2-level decomposition was performed and the norm, variance and standard deviation were extracted from the wavelet coefficients at the first level (L1) and second level (L2) detail components. In the previous research on wavelet feature extraction for melanoma, the entire image, including the surrounding skin was used in wavelet decomposition [10]. If the surrounding skin is non-uniform and noisy, that could yield unreliable results. In the current method, all of the background skin and the immediate edges between the surrounding skin and the lesion were masked out so that the coefficients represent only the inner texture.
image
A total of 18 features (norm, variance and standard deviation of the horizontal, vertical and diagonal components of the L1 and L2 wavelets) were extracted from 2D wavelet decomposition. Since the number of features is large, there is a high probability that the neural networks could get overwhelmed with the information from the similar inputs. To mitigate this, principal component analysis (PCA) is applied to the feature set [25]. PCA is a statistical method that constructs a new set of linearly uncorrelated variables, called principal components, by doing orthogonal transformation on the original set of statistically correlated variables. The transformation is done such that the first principal component has the largest variance, and each succeeding component in turn has the highest possible variance, within the constraint that each principal component be completely uncorrelated to the preceding components. PCA also eliminates those input components that contribute least to the variation in the dataset. PCA techniques are widely used to reduce the dimensionality in the input space in many applications including image compression and artificial neural networks. PCA analysis (using MATLAB functions) was performed on these 18 wavelet features by first normalizing the features so each has zero mean and unity variance. This analysis yielded 4 principal components. Figure 13 is a plot of the first principal component of the wavelet features PCA analysis.
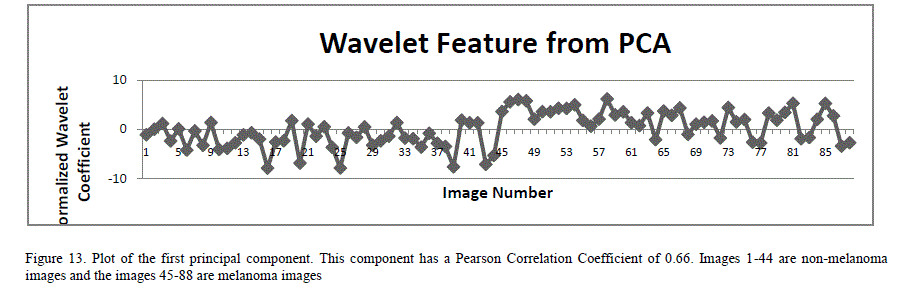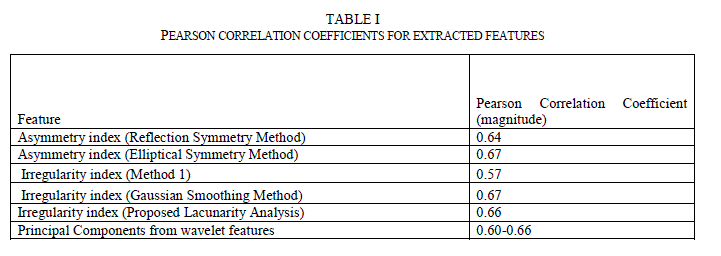
image
C. Feature Correlation to Classification Results Many methods are available to find the correlation between two sets of variables. Pearson Correlation is one of the widely used methods. Pearson Correlation coefficient is a measure of linear correlation between two variables. If the correlation coefficient is 0, there is no correlation. A correlation coefficient of 1 indicates a strong positive correlation and a value of -1 indicates a strong negative correlation. Since these images from the data set were already preclassified by the experts, the correlation coefficient between the computed feature indexes and the classification results were analyzed. Table 1 lists the correlation coefficients. As can be seen, all chosen features have correlation coefficients between 0.57 and 0.67.
image

VII. NEURAL NETWORK ARCHITECTURE
A single stage feed forward neural network classifier containing one input, one hidden and one output layer was predominantly used in previous research for lesion classification and sensitivities between 80-90% were reported [6]. A single stage neural network takes longer to train as the number of variegated inputs increases. There is limited research on the impact of various neural network architectures on the classification accuracy of skin lesions. Ballerini et al. [2] proposed a K-NN classifier that did the coarse classification first followed by finer classification to classifiy the lesions into various categories. Their system achieved a sensitivity of 76%. We attempted to improve the sensitivity of neural networks by experimenting with two different architectures – hierarchical and chained neural networks. D. Hierarchical Classifier The hierarchical neural network borrows from the concepts of statistical consensus theory and stacked generalization: in such a system, outputs of multiple “expert” neural networks are fed as the inputs of a new neural network [26]. To apply this concept, the features were classified into three main categories: contour, color and texture. Features extracted for measuring asymmetry and border irregularity were grouped into the contour features category. Features extracted from 2D wavelet transformation were grouped into the texture features category. The color category contains the one feature indicating the number of distinct colors in the image. Figure 14 illustrates the division of features between the different classifiers in our hierarchical classifier.
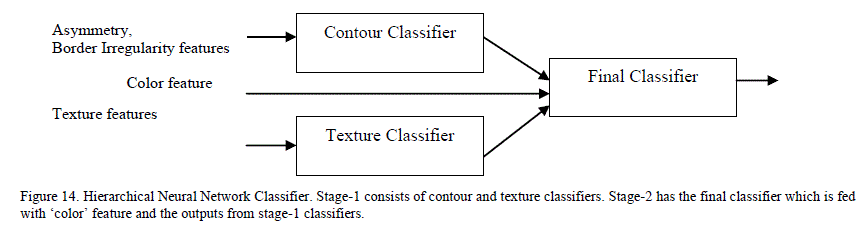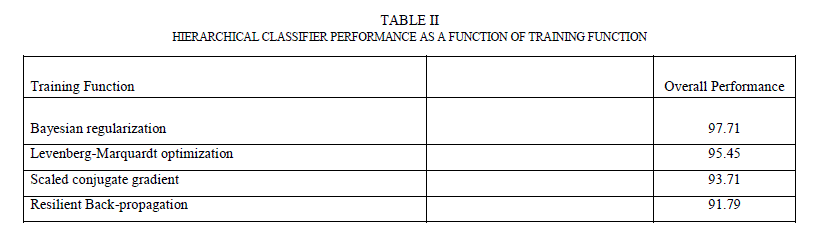
image
Hierarchical classifier has two stages. In stage 1, it has contour and texture classifiers and a final classifier in stage 2. Contour classifier is a single stage neural network classifier which is fed with all the contour features (asymmetry, border irregularity). It does PCA analysis on the features before feeding them to the neural network. Texture classifier is a single neural network classifier that is fed with extracted wavelet features. It does PCA analysis on these features (described in Section 5.4) before feeding them to the neural network classifier. By using separate classifiers for similar features, each classifier essentially became an “expert” in its field of analysis. The outputs of these two classifiers, along with the number of colors found, were fed to a third neural network classifier (in stage 2) that did the final classification based on the stage 1 classification results and the color feature. The accuracy of any neural network classifier depends on the type of neural network, the number of hidden layers and the hidden neurons and training function used. A feed forward neural network with back-propagation was used for each classifier. For training function, four most widely used training algorithms were analysed. Table II shows the overall performance (which is the percentage of the total images correctly classified in the complete data set) as a function of the training function. From the results, Bayesian regularization with Levenberg –Marquardt optimization has the most optimal performance. In this training function, the weights and biases are updated according to Levenberg-Marquardt optimization and the function tries to minimize a linear combination of squared errors and weights in such a way that the resulting network has the ability to generalize [27]. To come up with the number of hidden neurons, the number of hidden neurons was varied between 1 and 30 and tested the performance for each of the stage-1 classifiers. It was found that the contour classifier had the best performance with 10 neurons and the texture classifier had the best performance between 7-10 neurons.
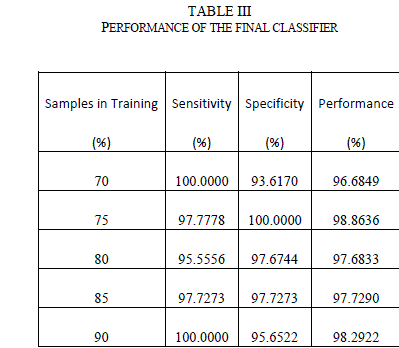image
image
The outputs from the stage-1 classifiers, along with the output from color feature were fed to the stage-2 or final classifier. The final classifier was able to achieve good performance with only 2 hidden neurons. The training function in MATLAB supports multiple methods to divide the inputs into training and testing sets. The percentage of samples in training was varied from 70% to 90% (remaining samples in testing) and the sensitivity, specificity and performance was noted down in Table III. As seen from the table, the network is able to generalize well, and is able to perform well above 95% sensitivity for these ratios. Since the sensitivity of the neural networks depends on the initial state and distribution of the data set between training and testing, the training needs to be repeated multiple times to get the average sensitivity of the classifier. The training was repeated 20 times with 90:10 ratio of training to test samples and got an average overall performance of about 98.9% with the architecture. E. Chained Classifier Zaamout and Zhang [19] discussed single link chain (SLC) neural network architecture where the predictions of a neural network were fed as inputs to another neural network trained on the same set of inputs and they showed that it improved the overall classification of the system. This concept was used to build a 2-stage chained neural network classifer as shown in Figure 15. Each classifer is a feed forward neural network with back-propagation, using Bayesian regularization as training function and 10 hidden neurons. Principal component analysis is done on all the features and the condensed feature set is given to the classifiers in both the stages. The output of the second classifier achieved an average overall sensitivity of 99.2% when the training is repeated 20 times.
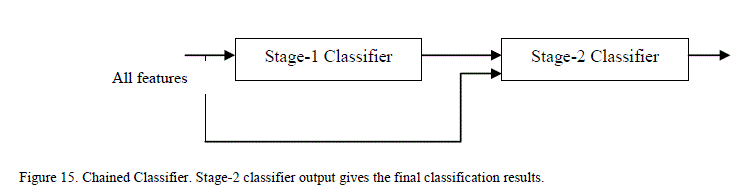image
Table IV shows the performance of the chained classifier as a function of the number of samples in the test data set. As seen from the table, the chained classifier is able to generalize well with sensitivity values well over 95% for all the cases.
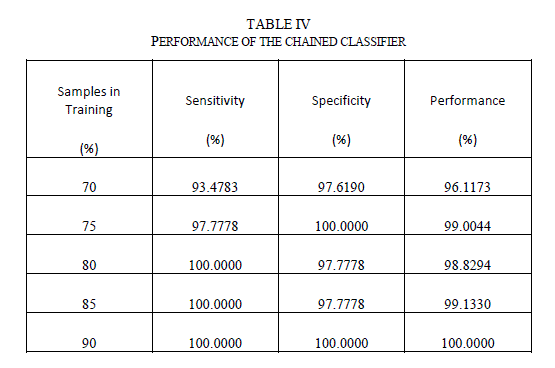image
F. Comparison of the neural network architectures Performance of a neural network classifier can be specified using various metrics. The terms mean squared error, sensitivity, specificity and confusion matrix were used widely. Sensitivity measures the proportion of the actual positives (in this case, diagnosis of the malignancy in the skin lesion) that are correctly identified as such. Specificity measures the proportion of the negatives that are correctly identified as negatives. The higher the sensitivity and specificity, the more accurate the classifier is. For medical image diagnosis, both sensitivity and specificity are important metrics. Higher sensitivity increases the chances of detecting melanoma quickly. Higher specificity reduces unnecessary biopsies performed on non-melanoma lesions. Table V below details the performance of various classifiers. For the comparison, a single stage classifier, which is a simple feed forward neural network classifier with 20 hidden neurons and Bayesian regularization as training function was also included. The number of hidden neurons for this classifier is selected based on the best performance when the training is repeated between 1-30 neurons. All the classifiers were trained with 90% of the data set and tested with remaining 10% of the data set. The training is repeated a minimum of 20 times by randomly choosing the training and testing images for each iteration. Average training and testing sensitivity, as well as overall performance was noted.
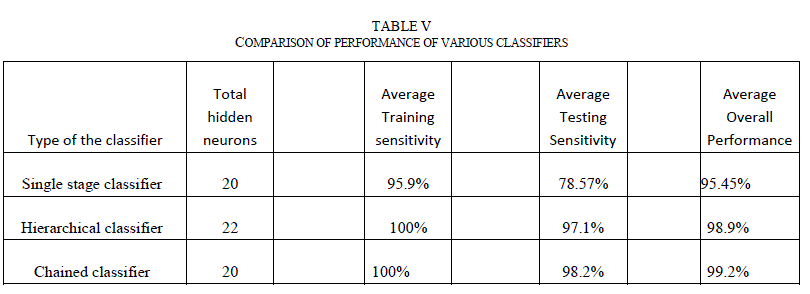image
As evident from Table V, even the single stage classifier was able to achieve greater sensitivities to the training images due to the fact that the classifier is fed with a comprehensive set of features. But, the classifier did not generalize well and its testing sensitivity is around 78.57%. Both hierarchical and chained classifiers achieved good sensitivities in both training and testing data sets, and demonstrated superior overall performance. G. Classifier Performance with Images from Internet The performance of the chained classifier was tested with images taken from the internet. For this purpose, 14 melanoma images and 10 benign moles and other non-melanoma images were selected from the web. They were taken from multiple sources [29, 30, and 31], each image is of different size and with different lighting conditions, and not all of them were necessarily dermoscopic images. All features were extracted from these images. Then, using the trained chained classifier system, the diagnosis was simulated for these new images. Out of the 14 melanoma images, 2 images were classified incorrectly. Out of the 10 non-melanoma lesions, one was classified incorrectly as melanoma. Table VI lists the incorrect classification results and the discussion.
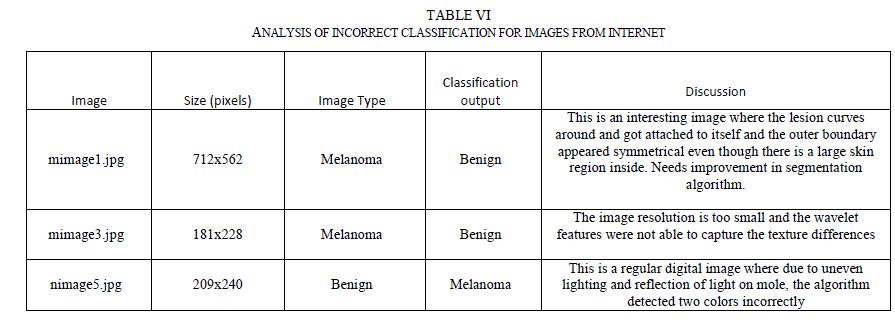image
One of the incorrect diagnosis happened for the image (mimage1.jpg in Table VI) where the lesion curved around and attached to itself like a donut shape. The segmentation algorithm failed to notice this and incorrectly segmented the image. The algorithm would be improved in future research to cover this condition. The other incorrect diagnosis was due to the fact that the image (mimage3.jpg) has a much smaller resolution than regular dermoscopic images and the wavelet coefficients were not able to capture the texture changes within the lesion. However, this is not a real concern with dermoscopic images as the resolution of dermoscopic images is much higher than 181 x228 pixels. Also, it was observed that regular digital camera images are of poor quality, with uneven distribution of light and this also leads to incorrect classification (as seen for nimage5.jpg). However, this is also not a real concern since the dermatoscope images do not have issues relating to light reflections and uneven lighting.

VIII. NOVEL DIAGNOSIS TOOL
Any research, however novel, has little practical value unless it is made available to the targeted audience and validated extensively. A novel approach to make this diagnosis tool widely available to physicians and dermatologists was proposed. The entire algorithm was written in MATLAB due to its powerful image processing and neural network tool boxes. However, we cannot expect dermatologists to understand and run MATLAB. One option that sounded very appealing was to create a standalone executable from the MATLAB code that could be run on various platforms without a MATLAB license. But, to create a standalone executable would require a MATLAB compiler that costs $5000. Due to the limited budget of our project, that option was ruled out. MATLAB software costs less than $200. We proceeded with the assumption that the end user (dermatologist/physician) should be able to afford it. Then, the challenge was to enable and empower them to use this algorithm with little or no MATLAB experience. Three simple MATLAB based applications were proposed to achieve this.
H. Melanoma Training and Diagnosis Tool
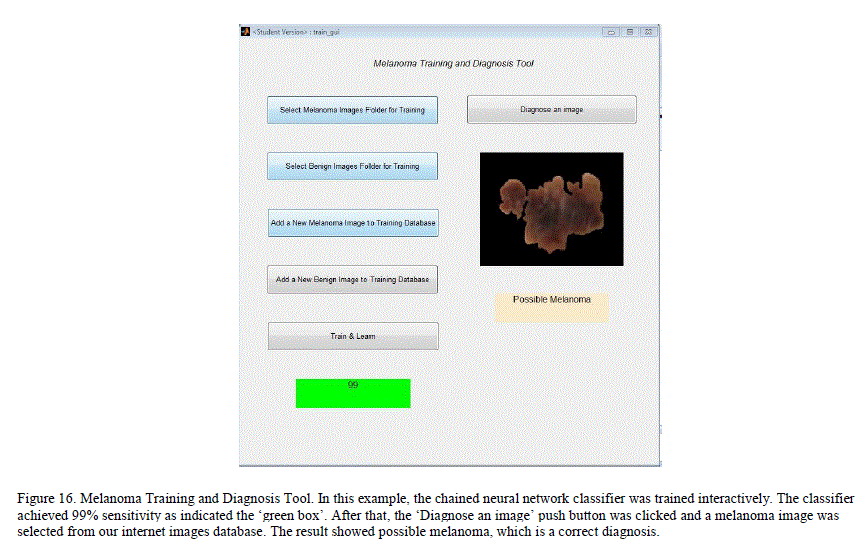image
A simple MATLAB GUI based application, which would let the user add new pre-classified dermoscopy images to the data set and train a chained classifier by simple push button knobs was created. After the training, the GUI can be used to diagnose a new image. By adding images and managing her training database, the user can expand his/her database and improve the classification results locally. Figure 16 illustrates the GUI and its knobs. I. Melanoma Diagnosis-Only Tool This is a simpler GUI based application for users who want a quick diagnosis without having to create or maintain their own training database. The application uses the trained neural networks state obtained from our system. The application simulates the neural network with the extracted features of the new image to get a diagnosis. This application does not require users to train the neural networks, and the results are obtained swiftly. Figure 17 illustrates the GUI for this tool.
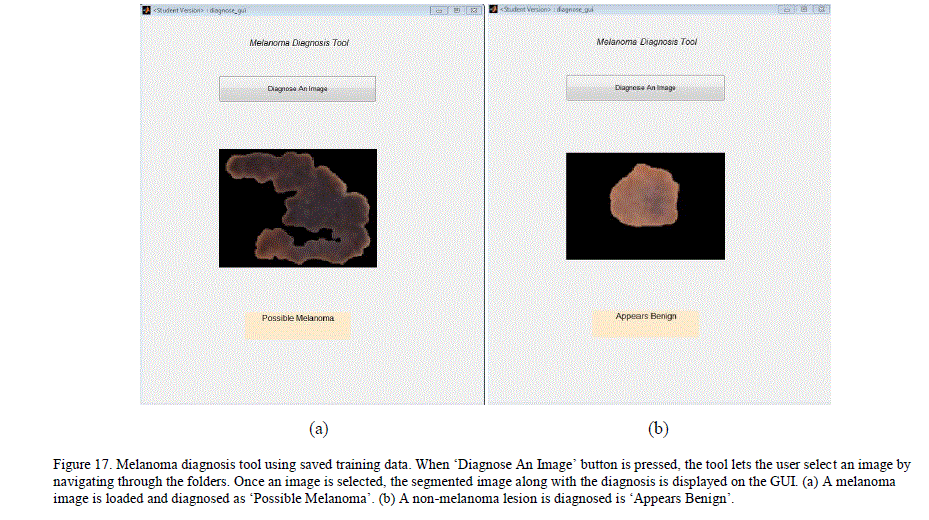image
J. Mobile Melanoma Diagnosis Application This is a novel method that enables dermatologists to take dermoscopic images and obtain an instant diagnosis, with a few simple steps on an iPhone. This method uses DermLite® DL1, which is a compact dermatoscope that can be attached to the iPhone. With this device attached to an iPhone, high resolution dermoscopy images can be captured. MATLAB software provides a mobile application that lets the user run the same MATLAB program in both the smart phone and the laptop as long as both these devices are on the same wireless network. There are many free (or relatively inexpensive) applications like “Dropbox” and “PhotoSync” which wirelessly transmit the images between smart phone and other devices connected on the same wireless network. Using these latest technologies, our method can obtain quick diagnosis using the steps below. 1. Install MATLAB on a laptop as well as on the iPhone and keep both the sessions open. 2. Install the „Diagnose_Melanoma‟ application in a folder and have the MATLAB point to that folder. 3. Take the picture of the skin lesion using „DermLite® DL1‟ attached to the iPhone. 4. Wirelessly transmit the picture to the folder in the laptop (where the „Diagnose_Melanoma‟ application is installed) using either “Dropbox” or “PhotoSync” applications. 5. Type the „Diagnose_Melanoma‟ in the MATLAB command line on the iPhone ( or on the laptop) 6. This pops up a segmented skin lesion image with a title that tells whether the lesion is melanoma or benign. In the „Diagnose_Melanoma‟ application, the stated of a trained chained neural network was saved and the application can simulate the new images using this trained data. This method was tried on two sample non-melanoma moles. Both results came out as negative for melanoma.
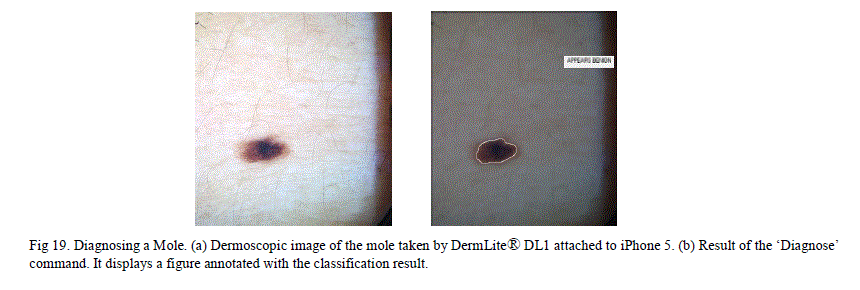image

IX. CONCLUSION
A system that automatically detects melanoma in dermoscopic images without any manual pre and post processing steps was developed. The proposed system consists of image segmentation; comprehensive feature set extraction and neural network classification. The proposed image segmentation algorithm successfully segmented all images (where the lesion was completely enclosed inside the image) in the data set. It identified all partial lesion images and flagged segmentation failures. For images with poor contrast, it was able to detect the segmentation failure in the first pass and correct it and segment successfully in the second pass. A new method called Elliptical Symmetry Method was proposed for quantifying asymmetry that involves fitting an ellipse around the image and finding the ratio of the sum of the non-overlapping regions between ellipse and the lesion to the overlapping area of the ellipse and the lesion. This technique can differentiate pear shaped and other nonelliptical shaped lesions as asymmetrical. It was shown that, this technique, combined with the Reflection Symmetry method gave a good overall performance. Two new methods to measure irregularity were proposed. The first one, Gaussian Smoothing Method, involved smoothing the contour and comparing the perimeter of the smoothed contour to the perimeter of the original lesion. The second method involved lacunarity analysis of the image borders. Both yielded good correlation to the classification results. A novel technique for extracting up to 4 distinct colors from the image was described. To improve the classification accuracy, two different multi-stage neural network architectures were explored. The hierarchical classifier did the initial classification using two classifiers; each was fed with a different set of the features. Final classifier used results from initial classification and the color information to further improve the classification accuracy. This hierarchical classifier achieved 98.9% overall performance with greater than 93% sensitivity and specificity for different training sample sizes. The chained classifier did the initial classification using all the features and the classification results were fed to the second stage along with the original features. This classifier achieved between 98.9% to 100% performance with greater than 95% sensitivity and specificities. Both classifiers did very well in testing samples sensitivity than the single stage classifier. These results show significant improvement in accuracy compared to previous research using neural networks by Ercal et al. [6] and Jaleel et al. [10]. A good sensitivity is important to reduce the false negatives. A good specificity is important to reduce the false positives, which would lead to unnecessary biopsies. Our system was able to achieve both the goals. Finally, simple diagnostic tools that would make this new algorithm usable readily in dermatologist‟s office were developed. The GUI based „Melanoma Training and Diagnosis Tool‟ allows dermatologists to add new images and improve the training accuracy in addition to diagnosing new images. The GUI based „Melanoma Diagnosis-Only Tool‟ has the saved training state from our data set and it lets the dermatologists diagnose a new image by simulating the trained neural network. The „Diagnose_Melanoma‟ application diagnoses the latest image in the folder where the application is loaded. This can be used in conjunction with iPhone attached dermatoscope to get instant diagnosis on an iPhone. These applications would be made widely available (by uploading them on MATLAB central – where users can share the applications).

X. FUTURE RESEARCH
A list of future enhancements under consideration: 1. Create a standalone executable for the algorithm using MATLAB compiler and distribute the executable freely. With a standalone executable, anyone would be able run the executable on the images to be processed without a MATLAB license. 2. Create an iPhone application with a standalone executable wrapped inside objective C that would give instant diagnosis without the need for wireless transmission of images between iPhone and laptop.

References
  1. Abbasi, R N, et al. "Early diagnosis of cutaneous melanoma - revisiting the ABCD criteria", The Journal of American Medical Association, Vol. 292, No. 22, pp. 771-2776, 2004.
  2. Ballerini, Lucia, et al. "Non-melanoma skin lesion classification using colour image data", IEEE International Symposium on Biomedical Imaging, pp. 358-361, 2012.
  3. Canny, john. "A computational approach to edge detection", IEEE transactions on Pattern Analysis and Machine Intelligence, Vol. 8, Issue. 6, pp.679-698. 1986.
  4. Celebi, M. E., W. V. Stoecker and R. H. Moss. "Advances in skin cancer image analysis", Computerized Medical Imaging and Graphics, Vol. 35, No. 2, pp. 83-84, 2011.
  5. Chen, Jixiang, et al. "Color analysis of skin lesions for melanoma descrimination in clinical images", Skin Research and Technology, Vol. 9, No. 2, pp. 94-104, 2003.
  6. Ercal, Fikret, et al. "Neural network diagnosis of malignant melanoma from color images", IEEE Transactions on Biolmedical Engineering, Vol.41, No. 9, pp. 837-845, 1994.
  7. Friedman, R J, D S Rigel and A W Kopf. "Early detection of malignant melanoma: the role of physician examination and self examination of the skin", CA: A Cancer Journal for Clinicians, Vol. 35, Issue. 3, pp. 130-151, 1985.
  8. Gilmore, Stephen, et al. "Lacunarity Analysis: A Promising Method for the Automated Assessment of Melanocytic Naevi and Melanoma", PLOS one, Vol. 4, No. 10, 2009.
  9. Gniadecka, M, et al. "Melanoma diagnosis by raman spectroscopy and neural networks: structure alterations in proteins and lipids in intact cancer issue", J Invest Dermatology, Vol. 122, No. 2, pp. 443-449, 2004.
  10. Jaleel, A, Sibi Salim and Ashwin R B. "Artificial neural network based detection of skin cancer", Internal journal of advanced reseach in electrical, electronic and instrumentation engineering, Vol. 1, Issue. 3, pp. 200-205, 2012.
  11. Lee, T, et al. "DullRazor: a software approach to hair removal from images", Computers in Biology and Medicine, Vol. 27, Issue. 6, pp. 533-543, 1997.
  12. Lee, Tim K, David I McLean and M Stella Atkins. "Irregularity index: A new border irregularity measure for curaneous melanocytic lesions", Medical Image Analysis, Vol. 7, Issue. 1, pp. 47-64, 2003.
  13. Nammalwar, Padmapriya, Ovidiu Ghita and Paul F. Whelan. "Integration of Colour and Texture Distributions for Skin Cancer Image Segmentation", Internation Journal of Imaging and Robotics, Vol. 4, No. A10, pp. 86-98, 2010.
  14. Otsu, Nobuyuki. "A threshold selection method from gray level histograms". IEEE transactions on Systems, Vol. SMC-9, No. 1, pp. 62- 66, 1979.
  15. Plotnick, Roy E., et al. "Lacunarity analysis: A general technique for the analysis of spatial patterns", Physical Review, Vol. 53, No. 5, pp. 5461-5468, 1996.
  16. Ruiz-del-Solar, Javier and Rodrigo Verschae. "Skin Detection using Neighborhood Information", Proceedings of the 6th International Conference on Automatic Face and Gesture Recognition (FG2004), Vol. 1, pp. 463-468, 2004.
  17. Stanley, R. Joe, Randy Hays Moss and Chetna Aggarwal. "A fuzzy based hostogram analysis technique for skin lesion descrimination in dermatology clinical images", Computerized Medical Imaging and Graphics : the Official Journal of the Computerized Medical Imaging Society, Vol. 27, No. 5, pp. 387-396, 2003.
  18. Xu, L, et al. "segmentation of skin images", Image and Vision Computing, Vol. 17, pp. 65-74, 1997.
  19. Zaamout, K and J. Z. Zhang. "Improving neural networks classification through chaining", Artificial Neural Networks and Machine Learning–ICANN 2012, Vol. 7553, pp. 288-295, 2012.
  20. W V Stoecker, W. W. Lee, and R.H Moss. “Automatic detection of asymmetry in skin tumors”, Computerized Medical Imaging and Graphics, Vol. 16, Issue.3, pp. 191-197, 1992.
  21. Wolf, Joel A., et al. "Diagnostic Inaccuracy of Smartphone Applications for Melanoma Detection", Jama Dermatology, Vol. 149, Issue. 4, pp. 422-426, 2013.
  22. Hartigan, John A., and Manchek A. Wong. "Algorithm AS 136: A k-means clustering algorithm", Journal of the Royal Statistical Society. Series C (Applied Statistics), Vol. 28, No. 1, pp. 100-108, 1979.
  23. Mäenpää, Topi, and Matti Pietikäinen. "Texture analysis with local binary patterns”, Handbook of Pattern Recognition and Computer Vision 3, pp. 197-216, 2005.
  24. Pizer, Stephen M., et al. "Adaptive histogram equalization and its variations", Computer vision, graphics, and image processing, Vol. 39, No. 3, pp. 355-368, 1987.
  25. Jolliffe, Ian. Principal component analysis. John Wiley & Sons, Ltd, 2005.
  26. Ozay, Mete, and Fatos Tunay Yarman Vural. "On the Performance of Stacked Generalization Classifiers", Image Analysis and Recognition. Springer Berlin Heidelberg, Vol. 5112, pp. 445-454, 2008.
  27. Bishop, M Christopher. Neural networks for pattern recognition. Oxford university press, 1995.