Axial Compressive Behaviour of Slender CFST
membersâAnalytical Investigation

K.Kalingarani; B. Shanmugavalli; Dr. M.C. Sundarraja

Axial Compressive Behaviour of Slender CFST membersâAnalytical Investigation

K.Kalingarani¹, B. Shanmugavalli² and Dr. M.C. Sundarraja³

Post Graduate Student, Department of Civil Engineering, Thiagarajar College of Engineering, Madurai, Tamilnadu, India
Research Scholar, Department of Civil Engineering, Thiagarajar College of Engineering, Madurai, Tamilnadu, India
Faculty, Department of Civil Engineering, Thiagarajar College of Engineering, Madurai, Tamilnadu, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Concrete-filled steel tubular columns possess excellent earth-quake resistant properties such as high strength and ductility and large energy absorption capacity. For concrete-filled steel tubes (CFST), inward local buckling commonly observed in bare steel columns is effectively prevented, giving a higher capacity. However if the concrete core and the steel tube are loaded simultaneously the steel tube expands more than the concrete core under moderate loads since Poisson’s ratio is higher for the steel section. Number of researches has been done on composite tubular columns. But they are mainly on short columns, subjected to axial or earthquake loading. The objective of this paper is aimed at deriving an analytical solution for the behaviour of slender concrete-filled steel tubular sections with normal strength concrete. Various available codes and literatures were compared for this purpose and based on this; experimental programs are proposed to be performed.

Keywords

CFST members, slender, compression, local buckling, axially loaded

INTRODUCTION

Concrete-filled steel tubes (CFST) are composite structures of steel tube and in-filled concrete. These members are ideally suited for all applications because of their effective usage of construction materials. Application of CFST concept can lead to 60% total saving of steel in comparison to a structural steel system concrete core enhances higher compressive strength, stiffness, damping and tensile strength by outer steel tube. Moreover, high strength CFST columns require a smaller cross-section to withstand load which is appreciated by architects and building engineers. The behaviour of CFST members in bending, shear, compression and fatigue resistance under cyclic seismic loading are also superior over reinforced members, hence widely used in earth-quake zones1. The steel concrete composite columns have several advantages such as high axial load carrying capacity, good ductility performance, energy absorption capacity ad high fire resistance as well as fast construction.

First research on CFST members was started by 20th century which mainly concentrated on strength capacity2. Furthermore, recent research focused on the use of high strength concrete which enhances the capacity of the section3-4. Behaviour and strength of materials are affected by the bond between steel and concrete, strength of materials, fire resistance, and confinement of concrete. The development of CFST members adds structural properties to the composite action. In which concrete core stiffened the steel tube and prevents the inward buckling. The steel tube acts as longitudinal and transverse reinforcement and also provides confining pressure to the concrete, which puts the concrete under a triaxial state of stress. The ultimate strength of CFST members depends on compressive strength of concrete and yield strength of steel tube.

Lu and Kennedy5 performed tests on twelve beams of concrete-filled steel square and rectangular hollow sections for determining the effects of different depth to width ratios and different values of shear span to depth ratio. The test results showed that the ultimate flexural strengths of the composite beams are increased by about 10%-30% over that of bare steel sections. CFST members are not only good in taking compressive force but also having capacity to resist tensile forces. Research by Pan and Zhong6 proved that tensile strength of circular CFST members is improved by 10% than hollow steel tubes. Different researchers concluded that confinement effectiveness is higher for circular steel tubes than rectangular or square steel tubes. Schneider7 studied the behaviour of short axially loaded concrete-filled steel tube columns. Fourteen specimens where tested to examine the effect of the tube shape and plate thickness of the steel tube on the column strength. It was found that circular steel tubes offer much post-yield axial ductility than square and rectangular tube sections. For this analytical study, three codes such as American Institute of Steel construction (AISC)9 , American Concrete Institute (ACI)10 and Eurocode (EC4)8 are used and comparison was made between them. Main purpose of this study is to study the influence of D/t ratio and L/D ratio of steel tube on the compressive behaviour.

II. ANALYTICAL STUDY

A. Eurocode 4

EC 4 uses limit state design concepts to achieve the aims of safety and serviceability by applying partial safety factor to load and material properties. Eurocode 4 is the only code that treats the effects of long-term loading separately. The ultimate axial capacity of CFST column given by EC 4 is as follows:

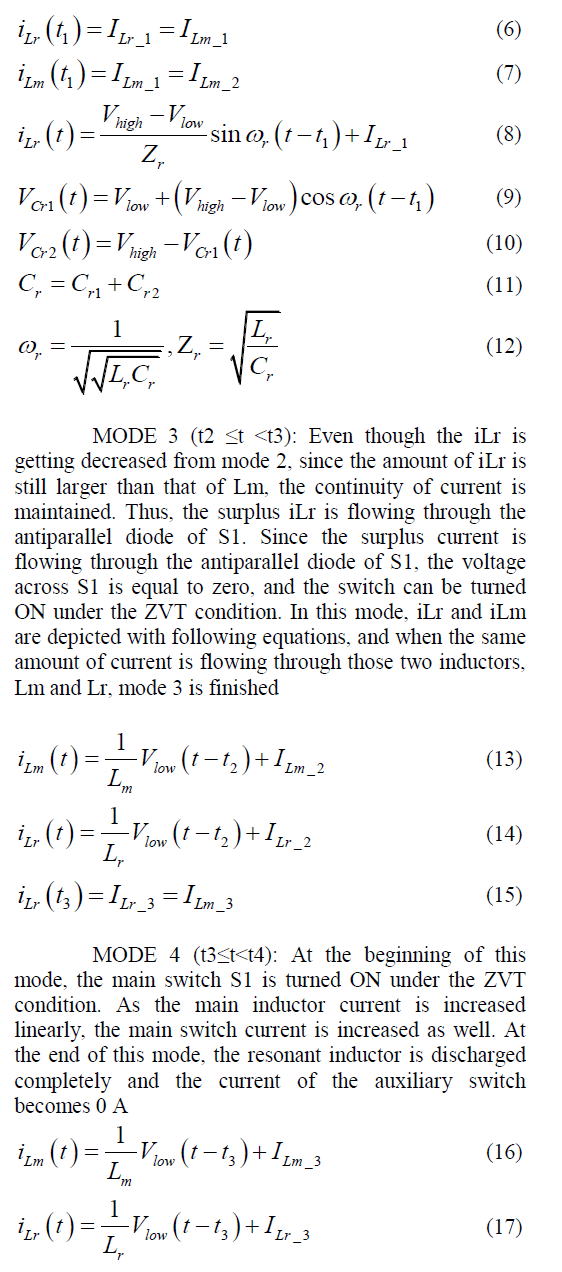Here Npl,Rd is replaced by Npl,R according to clause 4.8.3.7 of the code when γma and γc are taken as 1. For slender columns under long-term loading, the creep and shrinkage of concrete will cause a reduction in the effective elastic flexural stiffness of the composite column, thereby reducing the buckling resistance. However, this effect is significant only for slender columns. As a simple rule, the effect of long term loading should be considered if the buckling length to depth ratio of a composite column exceeds 15. The effect of long term loading may be ignored for concrete filled tubular sections with λ ≤ 2.0 provided that δ is greater than 0.6 for braced (or non-sway) columns. According to EC 4, clause 4.8.3.8, the resistance of members to axial compression is given by Nsd ≤ χNpl, Rd where χ is the reduction coefficient for the relevant buckling mode given in EC 3 in terms of the relative slenderness λ and the relevant buckling curve.

The theoretical capacity of CFST sections are calculated using Eurocode 4 and results are tabulated in Table 1 and the theoretical capacity of sections based on D/t ratio is shown in Fig.1. From that it can be easily understood that the axial load carrying capacity of sections is increased with the increase in D/t ratio.

B. ACI 318-1999: American Concrete Institute-Building code requirements for Structural Concrete

A composite column can be defined as a concrete column reinforced with a structural steel shape or tubing in addition to reinforcing bars. Slenderness effects are included by considering equivalent radius of gyration and flexural stiffness. The limiting value of D/t ratio beyond which the local buckling may be avoided is also specified for concrete filled tubes. Also long term effects such as creep of concrete under sustained loads are considered. The ultimate load, Pu is given by equation (4),

The theoretical capacity of CFST sections are calculated using ACI 318-1999 and results are tabulated in Table 1. From that it can be easily understood that the axial load carrying capacity of sections is increased with the increase in D/t ratio.

C. AISC-2005: American Institute of Steel Construction- Load and Resistance Factor Design Specification for Structural Steel Buildin gs

The plastic stress distribution method is adopted by the AISC code to determine the nominal strength of composite sections but suitable reduction factors are applied to account for slenderness ratio. Of course, local buckling should be considered for filled composite members when using this method. The AISC specifies that for the plastic stress distribution method, the steel tube reaches its yield stress (fy) when concrete infill strength is about 0.95fc’. Local buckling of CFST members should be accounted through classification of these composite sections into: compact, non-compact or slender. The element is considered to be compact if its D/t ratio is less than λp and to be noncompact if its D/t ratio is more than λp but less than λr. Moreover if the section’s D/t ratio exceeds λr then it is classified as slender. In any case the maximum permitted D/t ratio should not exceed 0.31E/fy in order for the AISC’s formulae to be applicable. Based on these limits, all the sections in the proposed experimental program are classified as slender since the D/t ratio is greater than λr. For the axially loaded CFST columns, the design compressive strength can be calculated for the flexural buckling limit state based on member slenderness as follows:

The design compressive strength Pd as per Clause I 2.2b is calculated from the following equations (5) to (11).

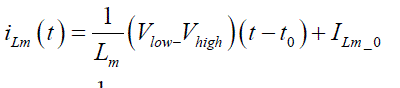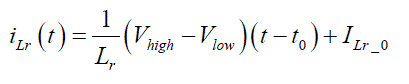The theoretical capacity of CFST sections are calculated using AISC and results are tabulated in Table 1. From that it can be easily understood that the axial load carrying capacity of CFST sections increased with the increase in D/t ratio.

III. COMPARATIVE STUDY

A. General

The ultimate capacity of different CFST sections based on their D/t ratio and L/D ratio were found according to Eurocode 4, ACI and AISC provisions. The theoretical capacity of CFST sections developed using all of the above codes denote that increase in D/t ratio enhances the capacity which is due to increased confinement pressure and decrease in L/D ratio also enhances the capacity of the section which is due to the slenderness effect.

B. Slenderness ratio of the Column

The length to width or diameter ratio (L/D) represents the slenderness of the column. The failure modes of concrete-filled short columns are characterized by yielding of steel followed by crushing of concrete. The strength increase will occur only for columns of smaller slenderness ratio (or L/D ratio). Columns with greater slenderness ratio fail by overall buckling. Hence it can be observed from the analytical results that the decrease in L/D ratio increases the capacity of the CFST section.

C. Diameter to Thickness ratio

The increase in D/t ratio may be either due to the increase in diameter or due to the decrease in thickness of the section. Hence it is analyzed by keeping the diameter constant and varying the thickness or by keeping the thickness constant and varying the diameter. The increase in D/t ratio with increased diameter for a constant thickness represents the improvement in cross section of the steel tube and hence produces greater section capacity. The increase in D/t ratio with decreased thickness for a constant diameter represents reduction in cross section of the steel and hence produces lesser section capacity.

D. Grade of Concrete

The strength of concrete core decides stiffness of CFST columns. Stiffness increases with increase in concrete strength but columns fail due to crushing of concrete exhibiting brittle behaviour when filled with high strength concrete. Moreover, stiffness loss is rapid; sometimes with axial strain reversal occurs for high strength concrete infilled tubular columns. But it is a fact that increase in concrete core strength increases the strength of filled columns to a larger extent, no matter of either D/t ratio or L/D ratio.

IV. CONCLUSIONS

Based on the analytical study for the calculation of theoretical capacity of CFST sections with reference to ACI, AISC and Eurocode for different D/t and L/D ratios, the following conclusions are made:

1. The theoretical capacity of CFST sections developed using all of the above codes denote that increase in D/t ratio enhances the capacity which is due to the increased confinement pressure when the diameter alone is increased. But increase in D/t ratio reduces the capacity of the section which is due to reduction in cross section when the thickness is reduced for a constant diameter.

2. The ultimate capacity of different CFST sections with varied L/D ratio denote that there exists enhancement in section capacity with reduced L/D ratio and the reason is attributed to the fact of slenderness effect.

3. The strength of concrete core greatly influences the theoretical section capacity CFST columns. Sections filled with high strength concrete exhibit higher section capacity.

4. All of the above codes agree with each other but EC 4 gives conservative results and it is concluded that EC 4 provisions may be used for further analytical study to develop an expression to predict the section capacity of strengthened CFST columns.

5. Experiments were planned accordingly to evaluate the analytical results.

References

1Xias, Y., He, W, Mao, X, Choi, K., and Zhu, P., (2005), “Confinement design of CFT columns for improved seismic performance”. Hunan University, China.
Knowles, R. B., and Park, R., 1969, “Strength of Concrete filled Steel Tubular Columns,” J. Structural Engineering., ASCE. 105(12), pp.2565-2587.
De Nardin S., and El Debs.A.L.H.C, 2007, “Axial Load Behavior of Concrete Filled Steel Tubular Columns”, Proc. Institution of Civil Engineers, Structures and Buildings, 160, pp. 13 – 22.
Cederwall K., Engstorm B., and Guauers M., (1990), “High strength concrete used in composite columns”, Proceedings of High strength concrete, 2nd International Symposium, Detroit, 195-214 (ACI-SP 121)
Lu YQ, Kennedy DJL, (1994), “The flexural behaviour of concrete filled hollow structural sections”, Canadian Journal of Civil Engineering, 21(1); 11-130.
Pan YH., Zhong ST., (1990), “Constitutive relation of concrete filled steel tube under tension”, Ind. Constr; 20(4):33-7
Schneider, S., 1998, “Axially Loaded Concrete Filled Steel tubes” ASCE. J. Structural Engineering., 124(10), pp.1125- 1138.
Eurocode 4: Design of Composite steel and concrete structures Part1-1: General rules and rules for buildings, EN 1994-1-1: 2004.
AISC: 2005, Load and Resistance Factor Design Specification for Structural Steel Building, American Institute of Steel Construction, Chicago.
ACI 318: 1999, Building Code Requirements For Structural Concrete and Commentary, American Concrete Institute, Farmington Hills, Mich.

Axial Compressive Behaviour of Slender CFST membersâAnalytical Investigation