ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
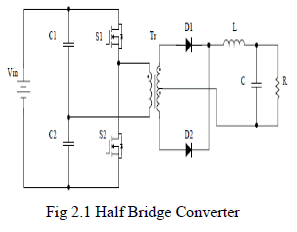
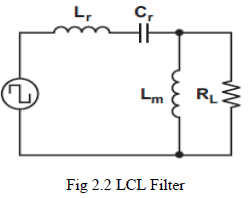
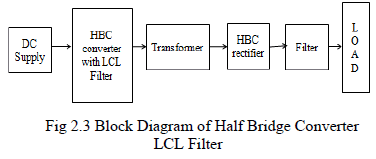
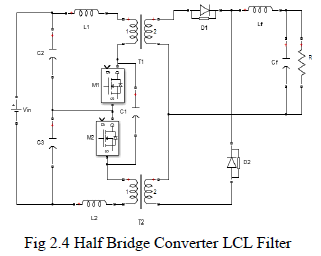
| Moazzam Aslam1, Nazrul Islam2, Mohd Moonis Zaheer3, Mehtab Alam2 Research Scholar, Department of Civil Engineering, Jamia Millia Islamia, New Delhi, 110025, India 1 Professor, Department of Civil Engineering, Jamia Millia Islamia, New Delhi, 110025, India 2 Associate Professor, Civil Engineering Section, University Polytechnic, AMU Aligarh, 202002, India3 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Articulated loading platform (ALP) is one of the promising compliant offshore structure and economically attractive for deep water conditions because of their lessened structural weight in comparison to conventional platform. The structure does not resist any force in bending due to wind, waves and currents rather forces are resisted by a large buoyancy force. In this paper, dynamic analysis of the tower under regular waves has been carried out with current forces. The Lagrangian approach has been applied for the derivation of nonlinear equations. The effects related to nonlinearity due to variable submergence, buoyancy, added mass, instantaneous position of the tower and relative-velocity squared drag force are considered in the analysis. NewMark’s-β integration scheme has been used for the solution of equation of motion in time domain. Modified Morison equation is used to model the fluid forces as these equations account for non-linearities associated with vortex shedding effects accurately in comparison to standard Morison equation. The Study has been carried out to compare the response of double hinged articulated tower under regular waves using Airy’s wave theory evaluated with Chakrabarti’s modification and that obtained by using Stokes’ fifth order nonlinear wave theory in the presence of ocean current. Stokes fifth order non-linear theory agrees closely in deep and intermediate water and it is found that for higher waves the difference in the values of responses obtained by Airy’s and Stokes’ are lesser while the difference is significantly higher for smaller waves. It is found that the deck displacement response as well as hinge rotation and hinge shear obtained using Stokes’ theory are lesser than that obtained using the Airy’s theory.
Keywords |
| Ocean currents; offshore structures; Dynamic analysis; Waves; Morison equation; Stokes’ theory |
INTRODUCTION |
| Articulated tower is one of the compliant offshore structure, economically attractive under deep water condition because of their lessened structural weight. Halvacioglu and Incecik (1990) studied the dynamic response of single and double hinged articulated tower subjected to wave and wind forces. They conduct their studies to predict the response of tower due to change in position of buoyancy chamber, hinge location and weight of deck paltform and concluded that due to change in position of buoyancy chamber, a significant change in natural frequency of tower was observed. Kim and Ran (1994) presented the responses of an articulated loading platform in random waves and currents both in frequency and time domain. They concluded from their numerical examples that slowly varying resonant responses in random waves are significant compared to wave frequency responses in case of no current or current normal to the wave direction. However, a great reduction observed when there exists strong in-line (coplanar or adverse) current. Islam et al. (2009 and 2012) studied the responses of single and double hinged articulated towers and compare under various ocean environments. Langrangian approach was used in deriving the non linear equations of motion. Pierson Moskowitz spectrum has been used in the characterization of sea state and Simiu’s spectrum has been used for the estimation of fluctuating wind. They concluded that wind effects are an important factor in determining the survivability of double hinged articulated towers in harsh offshore environments. Murtedjo et al. (2005) presented the study regarding the effects of buoyancy variations towards the dynamic behaviour of articulated tower for both regular and random wave. The authors found that by +/- 20% change in the outside diameter of the tower shaft ,the natural frequency get affected by as much as +/- 27.3% . They also found that by increasing the outside diameter by 20% the exciting moment energy will get increases by 28.2% and by decreasing the outside diameter by 20% the exciting moment energy will get decreased by 22.4%. Variations in the buoyancy chamber length gave the same effect but that is smaller than varying the outside diameter. The authors concluded that Articulated towers are very feasible to be operated at extreme wave condition because of their relatively small natural frequency and maximum response amplitude operator (RAO). Nagamani and Ganapathy (2000) studied a three legged articulated tower using analytical and experimental techniques. The authors also presented the effects of mass distribution on the variations of bending moment and the deck accelerations. The model was tested in a 2m flume for various wave frequencies and wave heights of regular waves. The authors concluded that the maximum bending moment along the legs increases with the wave frequency and decreases with the natural frequency of the tower also the bending moment increases with wave height for all the three legs. They further concluded that the deck acceleration increases with wave height and decreases with the natural frequency of the tower. Chandrasekaran et al. (2007) presented the response behaviour of TLP under regular waves using Stokes theory by considering the coupling between various degrees of freedom. They considererd the various nonlinearities developed due to change in tether tension, change in buoyancy and hydrodynamic drag force. They performed studies under regular waves using both Airy and Stokes theory. They concluded that the coupled response in surge and pitch degree of freedom obtained using Stokes theory is lesser than that obtained by the Airy theory. This paper is a second part of a comprehensive study on the comparative response obtained as per Airy’s and Stokes’s theory in the presence of ocean current. In the previous study the comparative response of Airy’s and stokes’s theory has been carried out in the absense of ocean current (see ref. [1]). The nonlinear equation of motion has been solved as per Lagrangian approach and NewMark’s β integration scheme has been used for the solution in time domain. |
II. PROBLEM DESCRIPTION |
| In the present study, a double hinged articulated loading platform (ALP) is modeled as an inverted double pendulum comprised of two universal hinges as shown in Fig. 1. It consist of a ballast chamber attached to the lower shaft of length L1 which is attached to the sea bed by a universal/articulation joint. The upper portion consists of a buoyancy chamber attached to upper column of length L2 which is connected to the lower shaft by another universal joint. The in-plane rotations at the two articulation points constitute the dynamic degree of freedom of the system. The system has two genralized coordinates; rotations θ1 and θ2 about the vertical axes. Following considerations are made in the structural modelling. |
| ïÃâ÷ A buoyancy force F, keeps the pendulum in a stable upright position. |
| ïÃâ÷ Fluid added mass is directly included in the inertia forces. |
| ïÃâ÷ Fluid inertia forces due to fluid acceleration and drag forces proportional to the square of the relative velocity between the fluid and the shaft are considered. |
| ïÃâ÷ Effect of collinear current on the water particle kinematics is considered. The equation of motion for the double hinged articulated tower under regular wave is given below: |
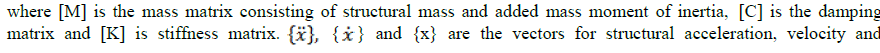 |
| displacement respectively. {F(t)} is the forcing function at any instant of time due to waves consisting of both drag and inertia forces. Drag and inertia forces are calculated by using Morison’s equation. |
| A. MASS MATRIX, M |
| The mass matrix of the ALP is presented below: |
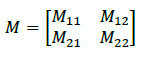 (2) (2) |
| where |
 |
| where is the total mass of upper tower evaluated as |
| (m2 + ma) and m2 is structural mass of upper tower. ma = mac + maf is the added mass of the structure. Where mac is the time invariant added mass up to MSL and maf is the fluctuating added mass which depends upon the variable submergence of the structure with respect to MSL with the passage of waves. |
| B. DAMPING MATRIX, C |
| The Coulomb damping matrix involves with the square term of velocity is as follows: |
 |
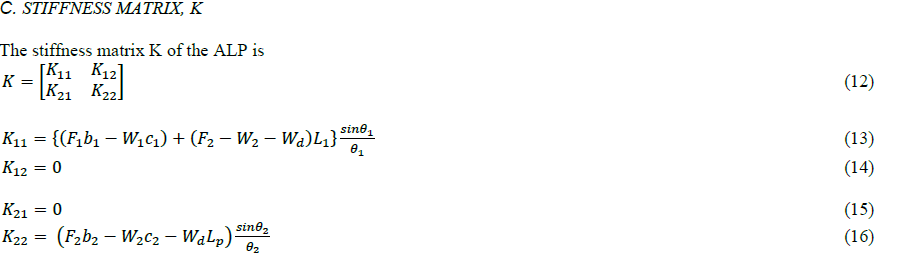 |
III. WAVE THEORIES |
| A. AIRY’S THEORY |
| A relatively simple theory of wave motion known as Airy’s linear theory has been given by G.B.Airy in 1842 (Dawson,1983). The theory assumes a sinusoidal wave form whose height H is small in comparison with the wavelength L and the water depth d. As per the Airy’s theory the sea surface elevation ( at given x and t is |
 |
| Where k =2π/L and ω= 2π/T The horizontal and vertical components of water particle velocities are as given below: |
 |
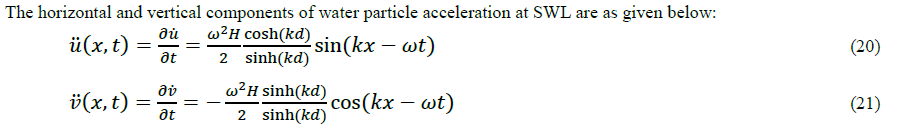 |
 |
| B. STOKES’ FIFTH ORDER NONLINEAR WAVE THEORY |
| According to Stokes fifth order nonlinear wave theory, the instantaneous vertical displacement of sea surface above the SWL is given as (Dawson, 1983) |
 |
IV. NUMERICAL STUDY |
| A double hinged articulated loading platform in 420 m water depth has been considered for the numerical study. The idealized tower consists of two segment vertical cantilever having a lumped mass at the top. Each cantilever is discretized in 50 elements. The characteristics of the platform and the environment used in the present study are same as used by “Islam, N., Zaheer, M.M. and Ahmad, S. (2009)”. The natural frequencies of the system for the two modes of vibration are 0.14 rad/s and 0.42 rad/s respectively. The dynamic response of double hinged articulated loading platform is obtained under regular wave with current 1.0 m/s with the use of Airy linear wave theory as well as the Stokes nonlinear wave theory. Two sea states are hereby considered for (H = 10m, T = 10s) and (H = 15m, T = 15s). The sea is simulated for the duration of one hour. It is important to mention here that simulated length excludes the initial transient non stationary phase of the responses due to initial conditions. |
V. SIMULATION RESULTS |
| The response of deck displacement, lower and upper hinge rotation, base and upper hinge shear for ALP under 10 m/10 s waves with current velocity 1.0 m/s is plotted. Fig. 2 show the response of deck displacement; Figs. 3-4 show the response of lower and upper hinge rotation; Figs. 5-6 show the response of base and upper hinge shear. |
 |
| It is seen from the plotted graphs that the maximum positive response obtained using Stokes’ fifth order nonlinear wave theory is less than those obtained from Airy’s linear wave theory with the Chakrabarti’s modification. |
 |
 |
| The response of deck displacement, lower hinge rotation, upper hinge rotation, base hinge shear and upper hinge shear for ALP under 15 m/15 s waves with current velocity 1.0 m/s is plotted. Fig. 7 show the response of deck displacement; Figs. 8-9 show the response of lower and upper hinge rotation; Figs. 10-11 show the response of base and upper hinge shear. |
 |
 |
 |
| The Table 1 and 2 shows the comparative statistical response obtained by both the theories in terms of mean, standard deviation, maximum and minimum values for 10m/ 10s and 15m/15s waves respectively with current 1.0 m/s. |
VI. CONCLUSIONS |
| Based on the performed analytical studies, the following conclusions are drawn: |
| 1. The response obtained using Stokes’s nonlinear wave theory for the hydrodynamic case of 10m/10s waves with current 1.0 m/s are lesser by 49%, 44%, 50%, 50% and 48% for deck displacement, bottom hinge rotation, upper hinge rotation, base hinge shear and upper hinge shear respectively in comparision to that obtained by using Airy’s linear wave theory with Chakrabarti’s modifications. |
| 2. The response obtained using Stokes’s nonlinear wave theory for the hydrodynamic case of 15m/15s waves with current 1.0 m/s are lesser by 20%, 14%, 19%, 20% and 22% for deck displacement, bottom hinge rotation, upper hinge rotation, base hinge shear and upper hinge shear respectively in comparision to that obtained by using Airy’s linear wave theory with Chakrabarti’s modifications. |
| 3. For the same water depth, it is seen that the responses under 10m/10s waves using stokes’ theory gives about 48% lesser values than that obtained by Airy’s wave theory, while for 15m/15s waves, the stokes’ theory gives about 19% lesser values than that obtained by Airy’s wave theory. |
| 4. For higher waves the difference in the values of responses obtained by Airy’s and stokes’ are lesser while the difference is significantly higher for smaller waves. |
 |
References |
|