e-ISSN: 2319-9849
e-ISSN: 2319-9849
General Chemical State Laboratory, Β’Chemical Service of Athens, An. Tsocha 16, Athens, Greece
Received date: 15/08/2018; Accepted date: 03/09/2018; Published date: 06/09/2018
Visit for more related articles at Research & Reviews: Journal of Chemistry
Oven drying at 105°C is considered as a method for the laboratory determination of the dry matter content. It is in this work applicable for papers and boards which do not contain other chemical substances, other than water, in order to determine its moisture content. This work is aimed to further apply the ISO approach into the laboratory using four paper substrates and to statistically analyse the results of the experiments. Importance is given as to the appropriate sampling procedure, as well as the conditioning of the quality control sample paper. The determinations of the moisture content are carried out in an oven at 105°C, for 16 hours. The analytical results show a moisture content of 4%-6%w/w for the paper substrates examined. The moisture content is finally expressed as a percentage mass fraction.
Moisture Content, Oven Drying, Paper and Board, Enthalpy Change, Heat Capacity, Expanded Uncertainty, Determination, Moisture Content.
An approach for calculating the expanded uncertainty in a chemical measurement of the moisture content of paper and board is described. The ISO approach is adapted to the analytical field. The procedure below estimates uncertainty from the information generated during the process of assessing precision. Generally, the moisture content of a lot of paper and board is determined quantitatively as water content, by oven drying, and is applied for a range of moisture content of 4.0%-6.0% w/w. The method is applicable for papers and boards which do not contain quantities of other chemical substances, other than water, which are volatile at the temperature of 105 ± 2°C. It is used in the case of paper and board samples taken for chemical and physical tests in a laboratory, when a determination of its dry matter content is required. It is a gravimetric method of analysis because it is based upon mass measurements with an analytical balance, an instrument that yields highly accurate and precise data.
Generally, the physical properties of paper are dependent on its moisture content. The moisture content of a paper sample is primarily dependent on the moisture of its surrounding atmosphere. The conditioning of a paper sample is a process of establishing a reproducible moisture content equilibrium between the sample of a paper and an atmosphere of specified temperature and relative humidity. In this work the specimens of the paper samples are brought in equilibrium with an atmosphere of specified temperature and relative humidity. The moisture content of a given paper sample in equilibrium with a given atmosphere varies according to whether the equilibrium is reached by sorption or by desorption of moisture. Usually the equilibrium condition is attained by the sorptive process. The system where the moisture is extracted from the paper samples is the oven. The heat supplied at constant pressure 1 bar=1 atm to the paper sample inside the oven (as the system does no additional work) is equal to a change in enthalpy, and is expressed as ΔΗ=qp (1) where ΔH is the change in enthalpy, and qp is the heat at constant pressure. Because the evaporation of water occurs at constant pressure the enthalpy change is equal to the heat supplied by the oven. The state function of enthalpy is related to the energy transferred as heat to the paper samples inside the oven at constant pressure 1 bar. In this paper also in order to examine the significance of differences between the means of moisture content of four different sample papers, one-way ANOVA is performed. It is examined if the differences between the means are statistically significant. We built an SPSS Pearson correlation table and we made a boxplot of the data from the experiments done. Also, the type A evaluation of uncertainty of the measurement of moisture content is performed. It is generally known that the standard uncertainty is the standard deviation of a probability density function. This probability density function is estimated by experiments. In this paper the measurements of the moisture content are repeated several times and the standard deviation of the obtained measurement results is calculated.
Instruments and Materials
A drying oven Memmert GmbH UNE 400 is used, which is capable of maintaining air temperature at 105°C ± 2°C and is ventilated to maintain uniform temperature and extract the moisture from the paper test pieces and it is accredited every three years. Glass containers NS ISOLAB Germany, with diameter of 80 mm, height of 30 mm, and capacity of 80 ml, inside which the paper test pieces are kept and weighed. Electronic balance Sartorius Basicplus, AGGöttingen Germany BP 221S, with maximum capacity 220 g, precision of four decimal places, and accuracy to 0.1 mg and it is accredited every three years. Glass desiccator, with a plate from porcelain with holes, and with CaCl2 as desiccant, for the transferring of the glass containers, inside which are kept the test pieces of the paper samples. Rubber gloves, clean and dry for the handling of the paper test pieces, and the glass containers are used. Conditioning chamber, that is capable of providing and maintaining standard conditions of temperature and humidity, where the paper test pieces are pre-conditioned at 23°C ± 2°C and 30% r.h. ± 5% r.h., and are conditioned at 23°C ± 1°C, and 50% r.h. ± 2% r.h. and is accredited each year. Relative humidity (r.h.) is the ratio, expressed as a percentage, of the actual water vapour content of the air to the water vapour content of air saturated with water vapour at the same temperature and pressure. Digital hygrothermometer, Amarell Germany AME 915000, with serial no DE75858615 (accredited every three years) inside the conditioning chamber, completely independent of the control system of the conditioning chamber, where the quality control sample test pieces are pre-conditioned and conditioned. The digital hygrothermometer is in continuous operation inside the conditioning chamber and it helps into better monitoring the operating conditions of the chamber. It responds rapidly into changes in relative humidity, namely less than 1 min for a change in relative humidity of 10%.
Sampling
Sampling from a lot is in accordance with the relevant ISO [1], for paper, board and tissue paper. From the copy paper A4 parcel we discard the three outermost sheets and we take four consecutive sheets, and from the selected layer of sheets we cut four sets of strips of width 50 mm and with their longer dimension in the cross-direction, one strip from each edge and two strips near the center. We then discard the top and bottom strips from each set of strips and the remainder together constitutes a test piece and it has a mass of approximately 3.0 g. For the board Bristol samples we cut strips from the sheets of the board, approximately 100.2 cm × 70.0 cm in dimension, with a 50 mm dimension in the cross-direction and 150 mm long with the short dimension parallel to the machine direction, which constitute a test piece with a mass of approximately 3.0 g. Also, from the roll of the tissue paper we take consecutive pieces of approximately 10.8 cm in length and 9.9 cm wide, which are quickly folded and enclosed into the glass containers and together constitute a test piece which has a mass of approximately 3.0 g.
Preparation of the Test Pieces of the Paper Samples
The determination of the percent moisture content in a paper sample is carried out twice. The test pieces of paper or board or tissue paper, and their weighing containers, are handled with clean, dry rubber gloves. The weighing glass containers are weighted empty, with 0.1 mg accuracy, and are kept closed, after been taken out from the desiccator. Then we press tare and we zero the indication of the balance. We then weigh a test piece in the closed, previously dried and weighed glass container. From the sample of paper we select test pieces of 3.0 g, with a 50 mm dimension in the cross-direction and approximately 150 mm long with the short dimension parallel to the machine direction. Both test pieces are quickly cut and weighed to minimize any variation in moisture content. We cut the sample of paper in order to determine the variation in moisture content of the sheets. Care is taken not to separate either the sheets or the strips comprising each set. We quickly fold the strips comprising the test piece, and enclose them in a glass container. We weigh the content of the container and we calculate the mass of the test piece at the time of sampling mo. We prepare duplicate test pieces on each position sampled, one comprising the strips near the center, and the other comprising the set of strips from each edge. Immediately after weighing we open the two containers and place them with test pieces and lids, in the oven.
Preparation and Conditioning of the Quality Control Sample
As for the test pieces of the quality control sample the sheets of the quality control copy paper-d are firstly preconditioned at 23°C ± 2°C and 30% r.h. ± 5% r.h. for 24 hours in a conditioning chamber [2]. The conditioning chamber can provide and maintain a temperature of 23°C ± 1°C and 50% r.h. ± 2% r.h. The test pieces of the quality control sample are set open and spread in the chamber in order to be exposed better in the conditioning atmosphere. They are then exposed in a conditioning atmosphere of 23°C ± 1°C, and 50% r.h. ± 2% r.h, for 8 hours. After the test pieces are hydrated and the equilibrium condition is attained by the sportive process, they are weighted and enclosed in two closed previously dried and weighed glass containers, with an accuracy of 0.1 mg. From the quality control sample of paper we also select test pieces of 3.0 g, with a 50 mm dimension in the cross-direction and approximately 150 mm long with the short dimension parallel to the machine direction.
Oven Drying
After weighing, the two glass containers are opened and the test pieces and lids are placed open and spread in the oven and are heated at 105°C ± 2°C, for 16 hours. The oven (Memmert GmbH UNE 400) used is capable of maintaining air temperature at 105°C ± 2°C and is ventilated to maintain uniform temperature and extract the moisture from the paper test pieces. During the drying period no new test pieces are put into the oven. Oven drying is extended for 16 hours, at a temperature of 105°C ± 2°C, until drying to constant mass [3,4]. After oven drying, we fit the lids on to the containers with the test pieces included, inside the oven, we take them out of the oven and we allow them to cool in the desiccator for 40 minutes. After cooling, we weigh the two containers and their contents, with an accuracy of 0.1 mg, and we calculate the mass in grams of the test piece after drying to constant mass m1. We carry out two determinations. Also, for the test pieces of the quality control sample, after cooling, again we weigh the two containers and their contents, with an accuracy of 0.1 mg, and we calculate the mass in grams of the test piece after drying to constant mass, for 16 hours.
Calculation of the Moisture Content in Paper Samples
The paper sample or board sample or tissue paper is initially weighted at the time of sampling mo, with its contained moisture, and it is weighted again after drying to constant mass m1, at a temperature of 105°C ± 2°C, for 16 hours. We calculate the moisture content wH2O, expressed as a percentage mass fraction, according to equation (1):
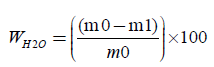 (2)
(2)
where, m0 is the mass of the test piece at the time of sampling, in grams (four decimals) m1 is the mass of the test piece after drying to constant mass, in grams (four decimals). For each glass container we calculate the moisture content. Finally we calculate the mean moisture content of the two parallel determinations, expressed as a percentage, rounded to the nearest 0.1%. The results of the two parallel determinations always are checked not to deviate by more than 0.5% mass fraction from their mean.
The validation of the quantitative method used to calculate the moisture content of paper and board, with oven drying at 105°C, contains the evaluation of the precision of the series of measurements done, and expresses the agreement of the results between themselves, and the determination of the expanded uncertainty of the analytical results. The precision of the method determines the accuracy of the method, alongside with the trueness of the method. An expression of the precision is the repeatability of the method.
Calculation of Enthalpy Change
The removal of the absorbed water from the different paper substrates is done by a reproducible procedure such as by heating to constant weight at 105°C. Generally the moisture content of the paper samples is markedly changed by variations in humidity and temperature. While the procedure of drying may not render the sample completely free of water, it usually lowers the moisture content to a reproducible level. The main mechanism of heat loss is through the evaporation of water. The study of the heat produced or required by a chemical reaction is called thermochemistry. A process that releases heat is classified as exothermic and one that absorbs heat is classified as endothermic. Because the absorption of heat results in an increase in enthalpy, an endothermic process is a process for which ΔH>0 (3). A change in enthalpy is equal to the heat supplied at constant pressure to the system, here 1 bar=1 atm. The heat capacity at constant pressure is used to relate the change in enthalpy to a change in temperature. If the heat capacity is constant over the range of temperatures of interest, then for a measurable increase in temperature ΔΗ=CpΔT (4) (at constant pressure 1 bar=105 Pa), where Cp,m(H2O, l)=75.3 J.K-1 mol-1, and T=378.15 K (105°C). The Cp,m(H2O, l) is the molar heat capacity at constant pressure 1 bar, Cp,m is the heat capacity per mole of water, and it is an intensive property. For copy paper-a sample, the increase in enthalpy at 378.15 K is 0.1709 KJ, for 0.1080 g of H2O vaporized (Table 1). For tissue-paper-b, the increase in enthalpy at 378.15 K is 0.2235 KJ for 0.1413 g of H2O vaporized. For paper board Bristol –c the increase in enthalpy at 378.15 K is 0.2489 KJ for 0.1574 g of H2O vaporized, which is the average mass of water vaporized in all six determinations of moisture content. Finally, for the copy paper quality control-d the increase in enthalpy at 378.15 K is 0.1903 KJ for 0.1203 g of H2O vaporized. The changes in enthalpy are reported for the process of drying of paper substrates because it takes place under a set of standard conditions. The temperature of the oven is kept constant at 378.15 K (105°C), in a specified volume of 0.053 m3, at 1 bar pressure. The standard enthalpy change for a reaction or a physical process is the difference between the products in their standard states and the reactants in their standard states, all at the same specified temperature. A standard enthalpy change is the standard enthalpy of vaporization Δvap° which is the enthalpy change per mole when a pure liquid such as water at 1 bar, vaporizes to a gas at 1 bar, as in H2O (l)→H2O(g) with Δvap°=+40.66 KJ.mol-1 at 373 K. The oven is actually an open system, and the main mechanism of heat loss is through the evaporation of water. So, from ΔΗ=nΔvap°=(m/M) Δvap° (5) we can calculate the grams of water vaporized for 16 hours needed to maintain constant temperature at 378.15 K (105°C), where m is the mass of water vaporized, M=0.018 Kg/mol is the molecular weight of the water. The mass of water that evaporated for 16 hours in order to maintain constant temperature at 105°C in the oven can be calculated for each of the four paper samples. For copy-paper-a sample the mass of water that must vaporize to maintain the temperature of the oven constant is calculated as 0.0757 g of H2O vaporized for 16 hours. The discrepancy between the mass of water actually vaporized and that of which the evaporation is needed to keep stable the temperature of the oven may be a result of the assumption that evaporation of water is the main mechanism of heat loss. It may be that carbon monoxide is lost simultaneously. For tissue-paper b the mass of water needed to vaporize is m=0.0989 g H2O for 16 hours, whereas more water is actually vaporized 0.1413 g of water. For paper board Bristol-c the mass of water needed to vaporize is m=0.1102 g H2O/16 hours, whereas more water is actually vaporized 0.1574 g. Finally, for copy paper quality sample-d, the mass of water needed to vaporize is m=0.0842 g H2O/16 hours whereas more water is actually vaporized 0.1203 g H2O (Figures 1-4).
| Number of tests | Copy paper-a, H2O in g | Tissue paper-b, H2O in g | Paper board Bristol-c, H2O in g | Copy paper - Quality control-d, H2O in g |
|---|---|---|---|---|
| 1 | 0,0809 | 0,1586 | 0,1564 | 0,1053 |
| 2 | 0,1038 | 0,1425 | 0,1597 | 0,0928 |
| 3 | 0,084 | 0,1563 | 0,1544 | 0,0924 |
| 4 | 0,0972 | 0,1728 | 0,1603 | 0,1399 |
| 5 | 0,1387 | 0,1561 | 0,1568 | 0,1239 |
| 6 | 0,1018 | 0,145 | 0,1565 | 0,1196 |
| 7 | 0,1177 | 0,1482 | 0,1167 | |
| 8 | 0,1205 | 0,0915 | 0,1388 | |
| 9 | 0,1213 | 0,106 | 0,1228 | |
| 10 | 0,0992 | 0,1358 | 0,1214 | |
| 11 | 0,1163 | 0,1329 | ||
| 12 | 0,1104 | 0,1373 | ||
| 13 | 0,0975 | |||
| 14 | 0,1353 | |||
| 15 | 0,1006 | |||
| 16 | 0,1059 | |||
| 17 | 0,1039 | |||
| 18 | 0,1152 | |||
| 19 | 0,0921 | |||
| 20 | 0,1103 | |||
| 21 | 0,1164 | |||
| Average | 0,1080 | 0,1413 | 0,1574 | 0,1203 |
| Variance | 0,0002 | 0,0006 | 4,971E-06 | 0,0003 |
| Sum | 2,269 | 1,4128 | 0,9441 | 1,4438 |
Table 1: The means of duplicate measurements of the masses of water extracted, by oven drying, in the paper samples in g.
Precision of the Measurements of Moisture Content
Analysis of variance
For the calculation of the repeatability, tests were carried out, where each test is the mean of duplicate measurements. Ten consecutive tests for the determination of moisture content, were carried out on the tissue paper-b, six tests were carried out on paperboard-c, and twenty one tests were carried out on copy paper A4-a. Also, twelve tests were carried out on quality control copy paper A4-d. All the means of the duplicate measurements done on all samples are shown in Table 2.
| Number of tests | Copy paper-a | Tissue paper-b | Paper board Bristol-c | Copy paper - Quality control-d |
|---|---|---|---|---|
| 1 | 4,2 | 6,42 | 4,58 | 5,66 |
| 2 | 4,13 | 6,63 | 4,52 | 5,6 |
| 3 | 3,83 | 6,08 | 4,5 | 5,48 |
| 4 | 4,05 | 6,31 | 4,48 | 6,05 |
| 5 | 3,99 | 5,21 | 4,5 | 5,87 |
| 6 | 3,88 | 5,51 | 4,7 | 5,92 |
| 7 | 4,15 | 5,62 | 5,61 | |
| 8 | 3,91 | 5,92 | 5,54 | |
| 9 | 4,1 | 5,85 | 5,31 | |
| 10 | 4,28 | 5,93 | 5,71 | |
| 11 | 4,36 | 5,93 | ||
| 12 | 4,5 | 5,81 | ||
| 13 | 4,63 | |||
| 14 | 4,91 | |||
| 15 | 4,61 | |||
| 16 | 4,51 | |||
| 17 | 4,67 | |||
| 18 | 4,39 | |||
| 19 | 4,37 | |||
| 20 | 3,56 | |||
| 21 | 4,72 | |||
| Sum | 89,75 | 59,48 | 27,28 | 68,49 |
| Average | 4,27 | 5,95 | 4,55 | 5,71 |
| Variance | 0,116705 | 0,187907 | 0,006827 | 0,046366 |
Table 2: The means of the tests of the moisture content done on the three samples of paper, and the quality control sample, for the determination of moisture content, where each test is the mean of duplicate measurements. Also, the sum and variance for each sample are calculated.
Analysis of variance (ANOVA) single factor
The technique used for the comparison of the means of many populations is called analysis of variance and is based on the comparison of variability between populations and the variability within populations [5]. If we admit that there is no variability between populations this does not mean that all our measurements are the same, but there is a possibility that they are different because of the random nature of our measurements. This last assumption leads us to the fact that there will be variability within each population which can be valued. An analog assumption we can have for the variability or variance between our populations. If the variabilities between our population and within are of the same size, then we conclude that there is not a difference between the means of our populations. If on the other hand the variability between our population is larger than the variability within our population, then we accept that the means of our populations are different. In the analysis of variance we assume k populations or groups with unknown means μ1, μ2, …, μκ, from which we take independently a random sample. The null hypothesis is H: μ1=μ2=…=μκ, while the alternative hypothesis A: at least one of the equalities does not apply.
We consider that independently random samples are taken from k normal populations with means μ1, … , μκ,
respectively and with common variance σ2. In this case we assumed that all our populations have equal variances. In
addition if ni, where i=1, … , k is the size of the sample from the io population, then the total number of our observations
is n=n1+…+nk. If Yij is the measurement of the jst statistical unit in the io population or group and 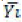 is the mean
of the same sample, then graphically we have the following Table 3.
is the mean
of the same sample, then graphically we have the following Table 3.
| Sample from population | |||
|---|---|---|---|
| 1 | 2 | ÃÆâÃâââ¬Ãâæ | k |
| Y11 | Y21 | ÃÆâÃâââ¬Ãâæ | Yk1 |
| Y12 | Y22 | ÃÆâÃâââ¬Ãâæ | Yk2 |
| ÃÆâÃâââ¬Ãâæ | ÃÆâÃâââ¬Ãâæ | ÃÆâÃâââ¬Ãâæ | ÃÆâÃâââ¬Ãâæ |
| Y1k1 | Y2m2 | ÃÆâÃâââ¬Ãâæ | Yknk |
 |
 |
ÃÆâÃâââ¬Ãâæ | 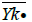 |
Table 3: Independently random samples taken from k normal populations In the analysis of variance we have to develop expressions for the variability between populations, and within the inside of each population.
In the analysis of variance we have to develop expressions for the variability between populations, and within the inside of each population.
The total variance, the variance between populations, and the within variance of our populations are calculated with the following equations:
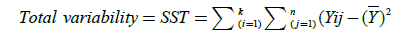 (6)
(6)
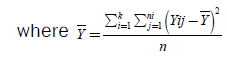 (7)
(7)
(Total Sum of Squares)
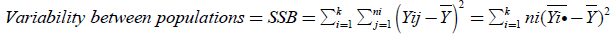 (8)
(8)
(Between Sum of Squares)
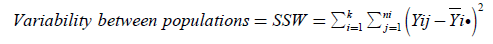 (9)
(9)
(Within Sum of Squares)
If then SSB is divided by n-k (within degrees of freedom), then the new expression which is acquired is 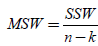 (10)
(10)
which is the within mean sum of the squares, whereas if SSB is divided by k-1, then the new expression that it emerges is 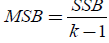 (11)
(11)
which is the mean square between populations.
In order to test the null Hypothesis H0:μ1=…=μκ against the alternative HA:at least one inequality, the quotient of
MSB (mean square between populations) divided by MSW (mean square within populations) is an F-statistic with k-1 and 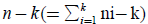 degrees of freedom. We thus approve the HA hypothesis if
degrees of freedom. We thus approve the HA hypothesis if
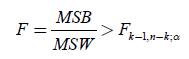 (12)
(12)
where as 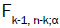 is the a point of an F distribution with k-1 and n-k degrees of freedom.
is the a point of an F distribution with k-1 and n-k degrees of freedom.
From Table 4, the ANOVA single factor, we observe that the between groups have F=89.622>Fcrit=2.812. which
means that 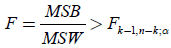 (13)
(13)
| ANOVA single factor | |||||||
| SUMMARY | |||||||
| GROUPS | Count | Sum | Average | Variance | |||
| a(Copy paper) | 21 | 89,75 | 4273809524 | 0,116704762 | |||
| b (Tissue paper) | 10 | 59,48 | 5,948 | 0,187906667 | |||
| c (Paper board-Bristol) | 6 | 27,28 | 4546666667 | 0,006826667 | |||
| d (Copy paper- Quality control) | 12 | 68,49 | 57,075 | 0,046365909 | |||
| ANOVA | |||||||
| SOURCE OF VARIATION | SS | df | MS | F | P-value | F crit | |
| SSB | BETWEEN GROUPS | 2730118643 | 3 | ÃÆââ¬Å¡Ãâà9100395476 | 8962152146 | 5,3E-19 | 28,11,544 |
| SSW | WITHIN GROUPS | 4569413571 | 45 | 0,101542524 | |||
| SST | TOTAL | 3,18,706 | 48 |
Table 4: Analysis of variance (ANOVA) single factor.
for a level of significance α=0.05. 0<α<1, and thus we approve the A, hyphothesis HA:at least one inequality exists between the means, μi≠μj, i,j=1,…,k, and we reject the null hypothesis Η0: μa=μb=μc=μd. Also the P-value=5.3E- 19<0.05=α, so again we reject the null hypothesis H0. This small P-value indicates a significant result. The main idea of ANOVA is to find how much of the total variance comes from the variance between the groups and from the variance within the groups. In the above measurements most of the variation is between groups, and this is a significant effect. Also in the above Table 4, the F value is high so the significance is low. For all the above, the assumptions that we have admitted are that: i) the populations have equal variances, and ii) the distributions of the populations are normal.
SPSS Pearson’s r and p-value
Below we also present the SPSS Pearson correlation (Table 5). The Sig(2-tailed) p-value tells us if our correlation is significant at an alpha level a=0.05. Here, because sig(2-tailed)=0.386>0.05 the test is not significant which means that there is a not significant relationship between the moistures of the copy paper a and tissue paper b. Similarly, because sig(2-tailed)=0.745>0.05 the test is not significant which means that there is a not significant relationship between the moistures of the copy paper a and paper board c. Finally, because sig(2- tailed)=0.520>0.05 the test is not significant which means that there is a not significant relationship between the moistures of the copy paper a and copy paper d. In the same table we have the Pearson’s r which is a measure of the linear correlation between each of the two samples of the total four papers. The values are between +1 and -1, where 1 is total positive linear correlation, 0 is no linear correlation, and -1 is total negative linear correlation. For example we have an r=0.309 between the moisture of copy a paper and the moisture of tissue b paper. But we have a negative linear correlation r=-0.172 between the moisture of copy a paper and the moisture of paper board c. Finally r=0.206 a positive linear correlation between the moisture of copy a paper, and the moisture of copy paper d.
| Correlations | |||||
|---|---|---|---|---|---|
| Moisturecopy a | Moisturetissue b | Moistureboard c | Moisturecopy d | ||
| Moisturecopya | Pearson Correlation | 1 | 0,309 | -0,172 | 0,206 |
| Sig. (2-tailed) | 0,386 | 0,745 | 0,520 | ||
| N | 21 | 10 | 6 | 12 | |
| Moisturetissueb | Pearson Correlation | 0,309 | 1 | -0,286 | -0,161 |
| Sig. (2-tailed) | 0,386 | 0,583 | 0,656 | ||
| N | 10 | 10 | 6 | 10 | |
| Moistureboardc | Pearson Correlation | -0,172 | -0,286 | 1 | 0,157 |
| Sig. (2-tailed) | 0,745 | 0,583 | 0,767 | ||
| N | 6 | 6 | 6 | 6 | |
| Moisturecopyd | Pearson Correlation | 0,206 | -0,161 | 0,157 | 1 |
| Sig. (2-tailed) | 0,520 | 0,656 | 0,767 | ||
| N | 12 | 10 | 6 | 12 | |
Table 5: The SPSS Pearson correlation table.
Box plot
The boxplot is a method for graphically depicting groups of numerical data through their quartiles. The Boxes and whiskers here, plot quartiles, and the band inside each box is always the second quartile (the median). The boxes edges are the 25th and 75th percentiles. The vertical size of the boxes are the interquartile range, or IQR. They measure the spread of the data, like a standard deviation. The whiskers, extending out of the boxes they represent the reasonable extremes of the data. That is, these are the minimum and maximum values that do not exceed a certain distance from the middle 50% of the data. Here we comment below on the data of the paper board c.
For paper board c we have n=6 measurements, arranged as 4.48, 4.50, 4.50, 4.52, 4.58, 4.70. Because n=6
then the 25% equals 6x(25/100)=1.5 and then 1.5 observations must be below the 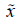 1/4, whereas 4.5 observations
must be above
1/4, whereas 4.5 observations
must be above 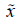 1/4. If we arrange our observations we have 4.50=
1/4. If we arrange our observations we have 4.50= 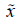 1/4=Q1, the first quartile, also known as
the 25th percentile. Inasmuch because of the symmetry
1/4=Q1, the first quartile, also known as
the 25th percentile. Inasmuch because of the symmetry 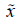 3/4=4.58=Q3 which is the third quartile, also known as
the 75th percentile, and then the interquartile range is
3/4=4.58=Q3 which is the third quartile, also known as
the 75th percentile, and then the interquartile range is 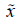 3/4-
3/4- 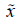 1/4=4.58-4.50=0.08. The median
1/4=4.58-4.50=0.08. The median 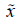 1/2 is a number
between 4.50 and 4.52. We take Q2=
1/2 is a number
between 4.50 and 4.52. We take Q2= 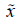 1/2=4.51, as the median also known as the 50th percentile. The minimum
score is 4.48, which is the lowest observation the “whisker” or flattened arrow extending out and below the box. Generally,
the graphical way to understand if an observation is limited is the boxplot diagram. A diagram like this contains
the lowest observation, the highest observation, as well as the 3 quartiles
1/2=4.51, as the median also known as the 50th percentile. The minimum
score is 4.48, which is the lowest observation the “whisker” or flattened arrow extending out and below the box. Generally,
the graphical way to understand if an observation is limited is the boxplot diagram. A diagram like this contains
the lowest observation, the highest observation, as well as the 3 quartiles 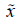 1/4,
1/4, 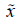 1/2, and
1/2, and 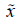 3/4. The boxplot for
paperboard c is built as follows: we put the five, above points on the horizontal axis and from a small height of the
vertical axis who crosses the horizontal at the lowest value, we draw a line parallel to the horizontal axis until the vertical
axis of
3/4. The boxplot for
paperboard c is built as follows: we put the five, above points on the horizontal axis and from a small height of the
vertical axis who crosses the horizontal at the lowest value, we draw a line parallel to the horizontal axis until the vertical
axis of 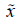 1/4. From point
1/4. From point 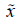 1/4, until point
1/4, until point 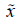 3/4, we draw an orthogonal parallelogram whose sides are two parts
from the verticals at points
3/4, we draw an orthogonal parallelogram whose sides are two parts
from the verticals at points 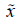 1/4, and
1/4, and 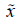 3/4. We then draw the median vertical at
3/4. We then draw the median vertical at 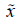 1/2, and we protrude the first
parallel=4.70 until the point where it meets the vertical at the maximum value. The value 4.70 is the maximum score
and in this box plot there are no values more than 1.5 times the interquartile range above Q3, in which, it is the third
quartile plus 1.5 times the interquartile range. Thus we have the above boxplot diagram for paper board c.
1/2, and we protrude the first
parallel=4.70 until the point where it meets the vertical at the maximum value. The value 4.70 is the maximum score
and in this box plot there are no values more than 1.5 times the interquartile range above Q3, in which, it is the third
quartile plus 1.5 times the interquartile range. Thus we have the above boxplot diagram for paper board c.
In the above Table 6 by Statistic we mean the descriptive statistics. The output has two columns the left column names the statistic and the right column gives the value of the statistic. By standard error we mean the standard error for the descriptive statistics. The standard error gives us some idea about the variability possible in the statistic. The mean is the arithmetic mean across the observations. It is the most widely used measure of central tendency. It is commonly called the average. The mean is sensitive to extremely large or small values. The 95% confidence interval for mean lower bound is the lower (95%) confidence limit for the mean, and it gives us some idea about the variability of the estimate of the true population mean. Here it has the value 4.46. The 95% confidence interval for mean upper bound, is the upper (95%) confidence limit for the mean and for the paper board c has the value 4.63. The 5% trimmed mean is the mean that would be obtained if the lower and upper 5% of values of the variable were deleted. If the value of the 5% trimmed mean is very different from the mean, this indicates that there are some outliers. For the sample of paper board c the 5% trimmed mean is 4.5419 and this value is not very different from the mean 4.5467. However, we cannot assume that all outliers have been removed from the trimmed mean. The median 4.51 can split the distribution such that half of all values are above the median, and half are below. The variance is a measure of variability and it is 0.007. It is the sum of the squared distances of data value from the mean divided by the variance divisor. Of course we don’t generally use the variance as an index of spread because it is in squared units. Instead, we use the standard deviation. The standard deviation is the square root of the variance and it is 0.0826. It measures the spread of a set of observations. The larger the standard deviation is, the more spread out the observations are. The minimum value 4.48 is the smallest value of the variable. The range is a measure of the spread of a variable. It is equal to the difference between the largest and the smallest observations (4.70-4.48)=0.22. It is very insensitive to variability. The interquartile range is the difference between the upper and the lower quartiles. It measures the spread of a data set and it has the value 0.12. It is robust to extreme observations. The skewness measures the degree and direction of asymmetry. A symmetric distribution such as a normal distribution has a skewness of 0, and a distribution that is skewed to the left, i.e., when the mean is less than the median, has a negative skewness. Here the skewness measure is 1.661>0 and the distribution is skewed. The kurtosis is a measure of the heaviness of the tails of a distribution. A normal distribution has kurtosis 0. Extremely non-normal distributions may have high positive or negative kurtosis values, while nearly normal distributions will have kurtosis values close to 0. Kurtosis is positive if the tails are “heavier” than for a normal distribution, and negative if the tails are “lighter” than for a normal distribution. Here the kurtosis measure is 2.518 and this positive value implies a leptokurtic distribution.
| Descriptive | ||||
|---|---|---|---|---|
| Statistic | Std. Error | |||
| Paperboard c | Mean | 4,5467 | 0,03373 | |
| 95% Confidence Interval for Mean | Lower Bound | 4,4600 | ||
| Upper Bound | 4,6334 | |||
| 5% Trimmed Mean | 4,5419 | |||
| Median | 4,5100 | |||
| Variance | 0,007 | |||
| Std. Deviation | 0,08262 | |||
| Minimum | 4,48 | |||
| Maximum | 4,70 | |||
| Range | 0,22 | |||
| Interquartile Range | 0,12 | |||
| Skewness | 1,661 | 0,845 | ||
| Kurtosis | 2,518 | 1,741 | ||
Table 6: The descriptive statistics for the moisture of the paper board c sample.
Percentiles
In the above Table 7 we present the weighted average for the four paper samples. These are the percentiles for the variable moisture of the four paper samples. Some of the values are fractional, which is a result of how they are calculated. There are several different ways of calculating these values, so SPSS clarifies what it is doing by indicating that it is using “Definition 1”.
| Percentiles | ||||||||
|---|---|---|---|---|---|---|---|---|
| Percentiles | ||||||||
| 5 | 10 | 25 | 50 | 75 | 90 | 95 | ||
| Weighted Average (Definition 1) | Copypaper a | 3,83 | 3,83 | 38,675 | 4,02 | 41,475 | . | . |
| tissuepaper b | 5,21 | 5,21 | 5,435 | 6,195 | 64,725 | . | . | |
| paperboard c | 4,48 | 4,48 | 4,495 | 4,51 | 4,61 | . | . | |
| Copypaper d | 5,48 | 5,48 | 5,57 | 5,765 | 59,525 | . | . | |
| Turkey's Hinges | Copypaper a | 3,88 | 4,02 | 4,13 | ||||
| tissuepaper b | 5,51 | 6,195 | 6,42 | |||||
| paperboard c | 4,5 | 4,51 | 4,58 | |||||
| Copypaper d | 5,6 | 5,675 | 5,92 |
Table 7: The Percentiles in SPSS.
In the same Table 7 we include the Tukey’s Hinges quartiles. These are the first, second and third quartile. These are calculated the way that Tukey originally proposed when he had the idea of a boxplot. These values are not interpolated but they are rather approximations that can be obtained with little calculation. We also have the percentiles and in these columns we have the values of the variables at various percentiles. These columns give us the distribution of the variable moisture. The percentiles are determined by ordering the values of the variable from the lowest to highest, and when we look at whatever percent we see the values of the variable. For example in the column labeled 5 the value of the variable copy paper a is 3.8. Because this is a weighted average, SPSS is taking into account the fact that there are several values of 3.8 which is why the weighted average is 3.83. The column 25 is the 25% percentile, which is also known as the first quartile. The column 50 is the 50% percentile which is also known as the median. It is a measure of the central tendency. It is the middle number when the values are arranged in ascending or in the descending order. There are times that this median value is a better measure of the central tendency than the mean. The median is a less sensitive value than the mean value to extreme observations. Finally in the above Table 7 we present the column 75 for the moisture of the four paper samples which is the 75% percentile, and it is also known as the third quartile.
Repeatability and interlaboratory reproducibility
Generally, the measurement precision, is a measure of how close the results of the measurements are to one another. It is expressed by statistical parameters which describe the spread of the results, typically the standard deviation, calculated from results obtained by carrying out replicate measurements on the material under specified conditions. The measurement repeatability is expected to give the smallest variation in results, and is a measure of the variability in the results of the measurements, when the measurement is performed by a single analyst using the same equipment over a short period of time. The interlaboratory repeatability contains the standard deviation under repeatability conditions, the repeatability limit r, and the coefficient of variance. The repeatability of the results of the tests are shown in Table 8.
| Sample | Number of tests | Mean of the Moisture content % | Repeatability standard deviation, sr | Repeatability coefficient of variation % | Repeatability Limit, r |
|---|---|---|---|---|---|
| Copy paper-a | 21 | 4,27 | 0,34 | 7,99 | 0,96 |
| Tissue paper-b | 10 | 5,95 | 0,43 | 7,29 | 1,20 |
| Paperboard Bristol-c | 6 | 4,55 | 0,08 | 1,82 | 0,22 |
| QC sample-copy paper-d | 12 | 5,71 | 0,22 | 3,77 | 0,60 |
Table 8: Precision of the procedure for the determination of moisture content.
Calculation of the type A expanded uncertainty
The expanded uncertainty is calculated from the following equations:
From equation (1) we have:
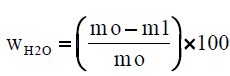 (14)
(14)
then,
The combined standard uncertainty is expressed as:
 (15)
(15)
whereas
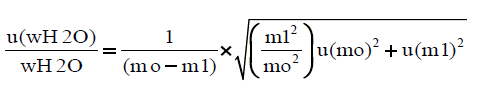 (16)
(16)
and finally
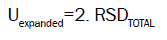 (17)
(17)
The RSDrMETHOD is calculated from the validation procedure of the method for the determination of moisture content, as RSDrMETHOD=sr × 100/mean (16), whereas sr=repeatability standard deviation, for each one of the samples tested, (Table 8). The RSDTOTAL and Uexpanded are procured from an excel sheet, where the uncertainty of the indication of the balance used is inserted. The uncertainty of the indication of the balance is given by the equation U(mg)=0.00016+0.00457 × m(g) (17) where U is the expanded uncertainty of the balance in mg, and m is the indication of the balance in g.
The combined standard uncertainty is multiplied by a coverage factor k=2 and then the expanded uncertainty is calculated. The expanded uncertainty Uexpanded is: Uexpanded=2. RSDTOTAL (18) (for confidence level 95%, and coverage factor k:2) [6].
Calculation of the Expected Value or Expectation of the Moisture Content of the Paper Samples
The mean or expected value or expectation E(X) of a random variable X can be calculated directly from the equation:
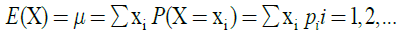 (18)
(18)
where X is a discrete random variable with a set of possible values x1, x2, x3, …. and probability mass function P(X=xi)=pi, where i=1, 2, 3, …
It is generally known that the standard uncertainty is the standard deviation of a probability density function. In this study the mean of the measurements for the determination of the moisture content for each sample tested, is multiplied by the expanded uncertainty of the measurement for the sample and then the uncertainty is calculated, and is added to the mean in order to obtain the expected value of the moisture content, for each one of the samples. From the above Tables 8 and 9, we have, for the copy paper-a sample the uncertainty value is (4.27 × 15.98%)=0.68% and the rounded expected moisture content is 4.3 ± 0.7%, for a confidence level of 95%. Similarly for tissue paper-b the uncertainty value is (5.95 × 14.58%)=0.87% and the rounded expected moisture content is 6.0 ± 0.9%, for a confidence level of 95%. For Bristol paper board-c the uncertainty value is (4.55 × 3.64%)=0.17% and the rounded expected moisture content is 4.6 ± 0.2% for a confidence level of 95%. Finally for the QC sample copy-paper-d the uncertainty value is (5.71 × 7.60%)=0.43% and the rounded expected moisture content is 5.7 ± 0.4% for a confidence level of 95%.
| Expanded Uncertainty | Copy paper-a | Tissue paper-b | Paperboard Bristol-c | QC sample-copy paper-d |
|---|---|---|---|---|
| For 95% confidence level | 15,98% | 14,58% | 3,64% | 7,60% |
Table 9: Calculation of the expanded uncertainties of the measurements of the moisture content %w/w.
In this work we examined the application of the oven drying at 105°C onto different paper substrates. Given that there has been an enormous increase in the number of paper samples measured in our laboratory for their moisture content to be determined, we further developed the method and calculated the expanded uncertainty of the measurement for each paper substrate. We have found that the mean moisture content %w/w varies from 4% w/w until 6% w/w, for the different paper substrates. Also the variance is calculated and we found that it varies for the four paper substrates examined from 0.19% until 0.01%. An analysis of variance (ANOVA) single factor was performed and we approved the alternative hypothesis and concluded that there exists one inequality between the means of the moisture content of the different paper substrates.
We built an SPSS Pearson correlation table and we concluded that there is not a significant relationship between the moistures of the four different samples of paper we examined. We made a boxplot of data from the experiments for the calculation of the moisture content. We commented on the construction of the box and whiskers of the moisture board c sample. We also included descriptive statistics for the paper board c sample and presented the percentiles and the Tukey’s Hinges quartiles. We also calculated the repeatability standard deviation sr and the repeatability coefficient of variation and the repeatability limit r of the four paper substrates. Finally the type A expanded uncertainty of the measurements of the moisture content was procured from excel spreadsheets, having taken into consideration the uncertainty of the indication of the analytical balance used. We calculated the expectation of the moisture content of the paper samples and we found that the expected values have similar dispersions.
Generally, the change from the concept of error to uncertainty is set by the publication in 1992 of the IEC-ISO “Guide to the Expression of Uncertainty in Measurement”. The new concept of uncertainty is introduced as a parameter associated with the result of a measurement that characterizes the dispersion of the values that could reasonably be attributed to the measurand [7]. This uncertainty is statistically determined in this study [8].
We suggested that the mechanism of extracting the moisture of paper samples inside the oven is by evaporation of water. We reported the change in enthalpy for that process which takes place under standard conditions such as temperature, volume and pressure. We also used the heat capacity at constant pressure to relate the change in enthalpy to the temperature used. We calculated the increase in enthalpy for the masses of water vaporized inside the oven. We also calculated the masses of water needed to vaporize in order to keep stable the temperature of the oven at 105°C.
Finally, in this paper the type A evaluation of uncertainty was performed and it was based on calculating the standard deviations of the means of a series of independent measurements of the moisture content in four different paper samples. An analysis of variance (ANOVA) was carried out in order to identify and quantify random effects in the measurements, and an SPSS Pearson correlation table was obtained, where the p-value shows no significant linear correlation between the different moistures of the four samples of paper. A Boxplot of distribution of percentiles for the data sets from the experiments for the calculation of the moisture content for the four different paper samples is presented, and descriptive statistics and Tukey’s Hinges quartiles were included. In this study we calculated the expanded uncertainties and also the expected values of the moisture content for all different paper samples. We concluded thus that the measurement of the uncertainty is necessary for a complete study of a quantitative determination of the moisture content, based upon mass measurements with an analytical balance.
In general, the result of a measurement is an approximation or estimate of the value of the specific quantity subject to measurement, and thus the result is complete only when accompanied by a quantitative statement of its uncertainty.