Research and Reviews - International Journals

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Characterization Theorems for Modular and Distributive Soft Lattices

E.K.R.Nagarajan1 and P.Geetha 2
  1. Associate Professor and Head,Centre for Research and Post Graduate Studies in Mathematics, Ayya Nadar Janaki Ammal College (Autonomous),Sivakasi ,Tamil Nadu, India
  2. Assistant Professor, Department of Mathematics, V.V.Vanniaperumal College for Women,Virudhunagar,Tamil Nadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Soft set theory was introduced by Molodtsov in 1999 as a mathematical tool for dealing with problems that contain uncertainty. Faruk Karaaslan et al.[6] defined the concept of soft lattices, modular soft lattices and distributive soft lattice over a collection of soft sets. In this paper, we define the concept of principle of duality in soft lattices and discuss some related properties of modular and distributive soft lattices. We also establish characterization theorems for modular and distributive soft lattices by their soft sublattices.

Keywords
Soft sets, soft lattices, soft sublattices, dual soft lattices, modular soft lattices, distributive soft lattices.

INTRODUCTION
Soft set theory was introduced by Molodtsov [9] in 1999 as a mathematical tool for dealing with uncertainty. Maji et al.[8] defined some operations on soft sets and proved related properties. Irfan Ali et al.[5] studied some new operations on soft sets. Li [7], Nagarajan et al.[10] defined the soft lattices using soft sets. Faruk Karaaslan et al.[6] defined the concept of soft lattices over a collection of soft sets by using the operations of soft sets defined by Cagman et al.[1]. In this paper, we define the concept of principle of duality in soft lattices and discuss some related properties of modular and distributive soft lattices. We also illustrate them with some examples. In addition, we establish characterization theorems for modular and distributive soft lattices by their soft sublattices.

SOME CONCEPTS IN SOFT SETS AND SOFT LATTICES
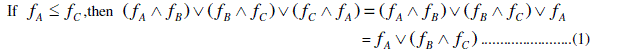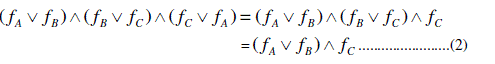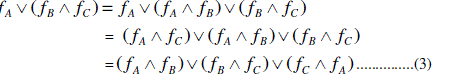image
image
image

MODULAR AND DISTRIBUTIVE SOFT LATTICES
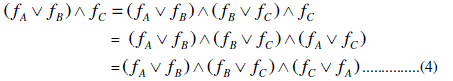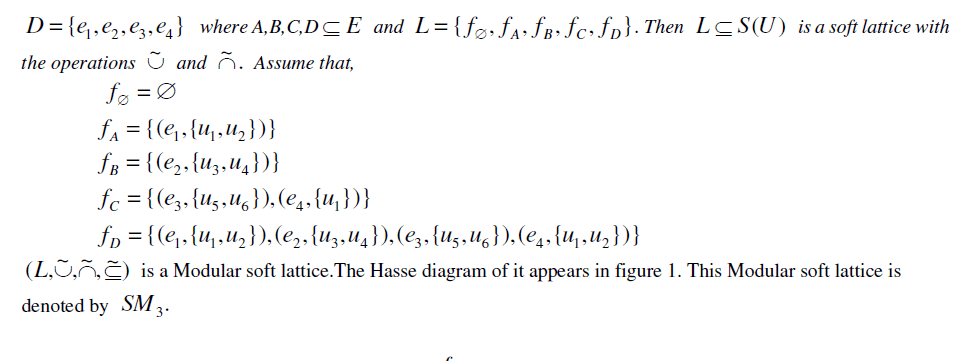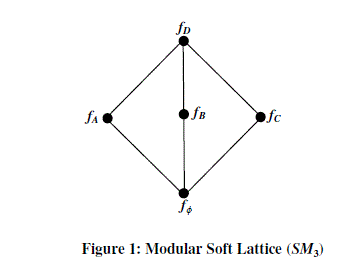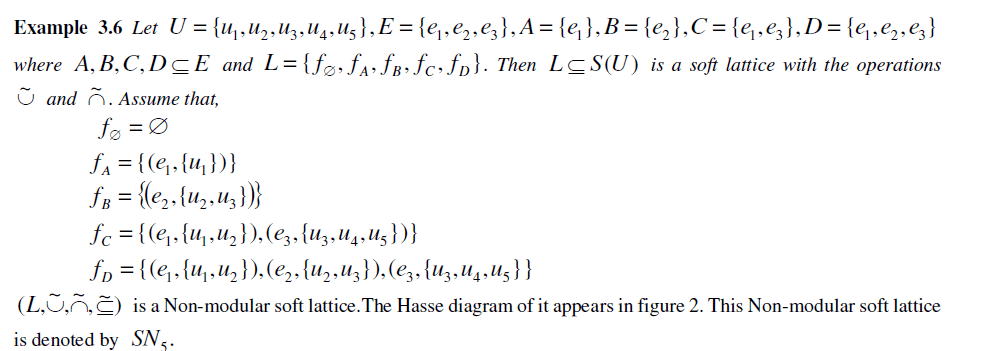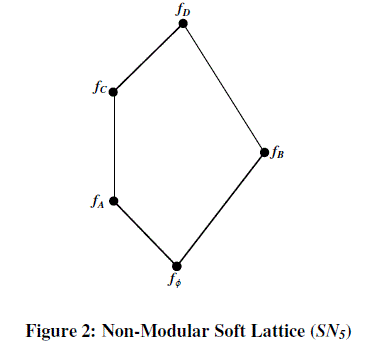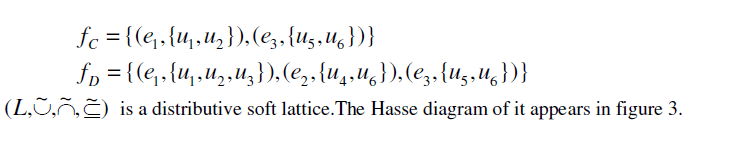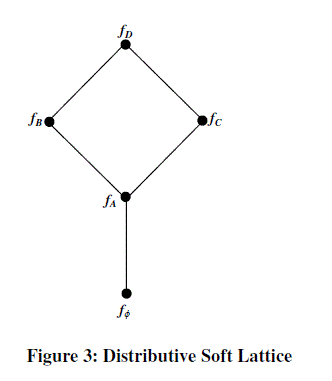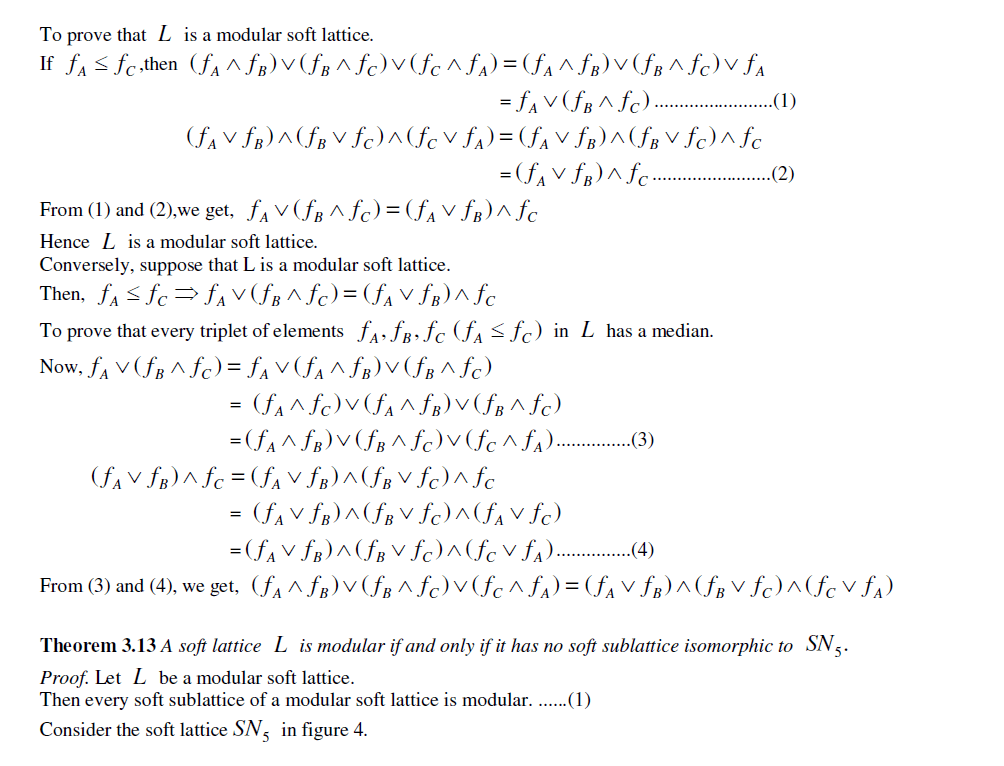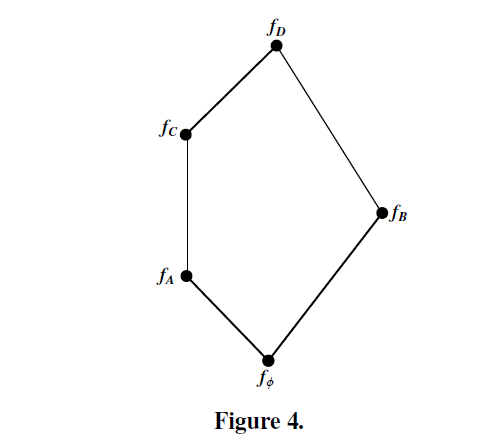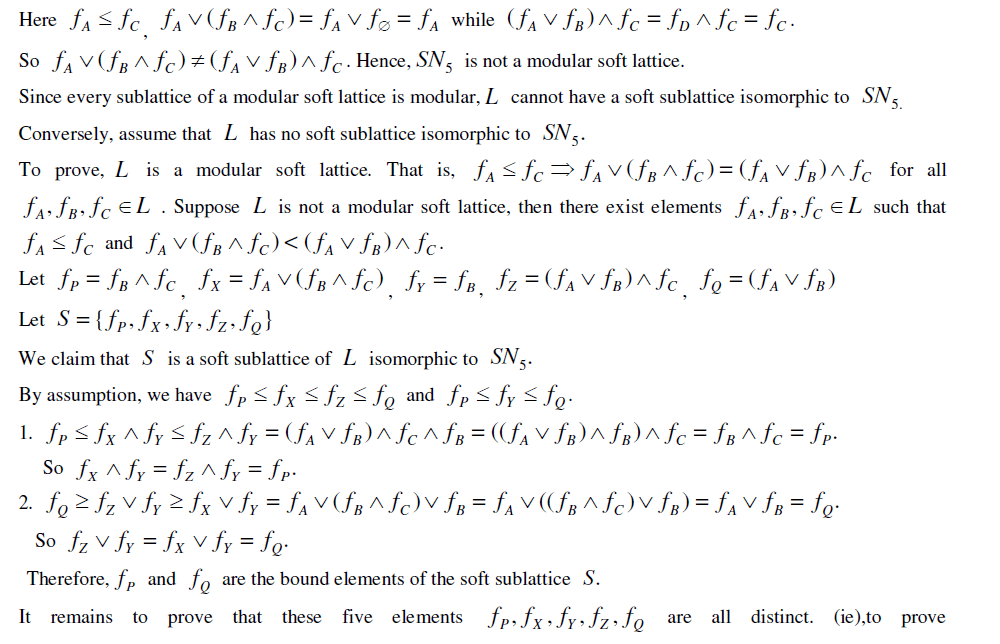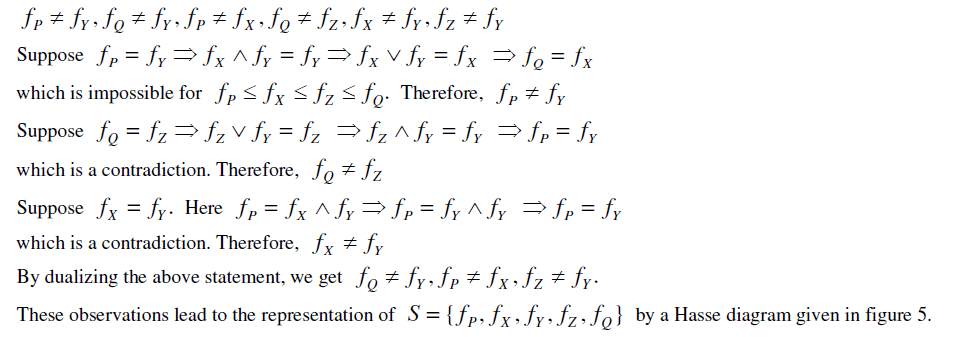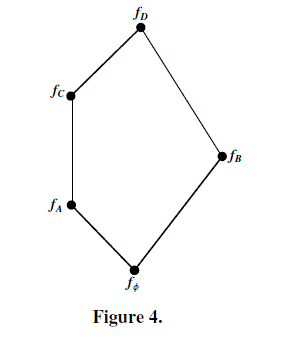image
image
image
image
image
image
image
image
image
image
image
imageimage
image
imagethe distributive soft lattice is distributive.
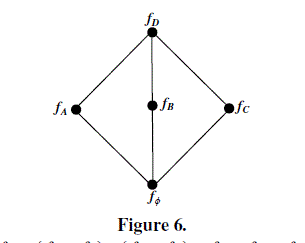
image
distributive soft lattice. Consider 3 SM in figure 6.
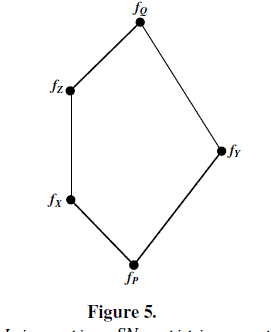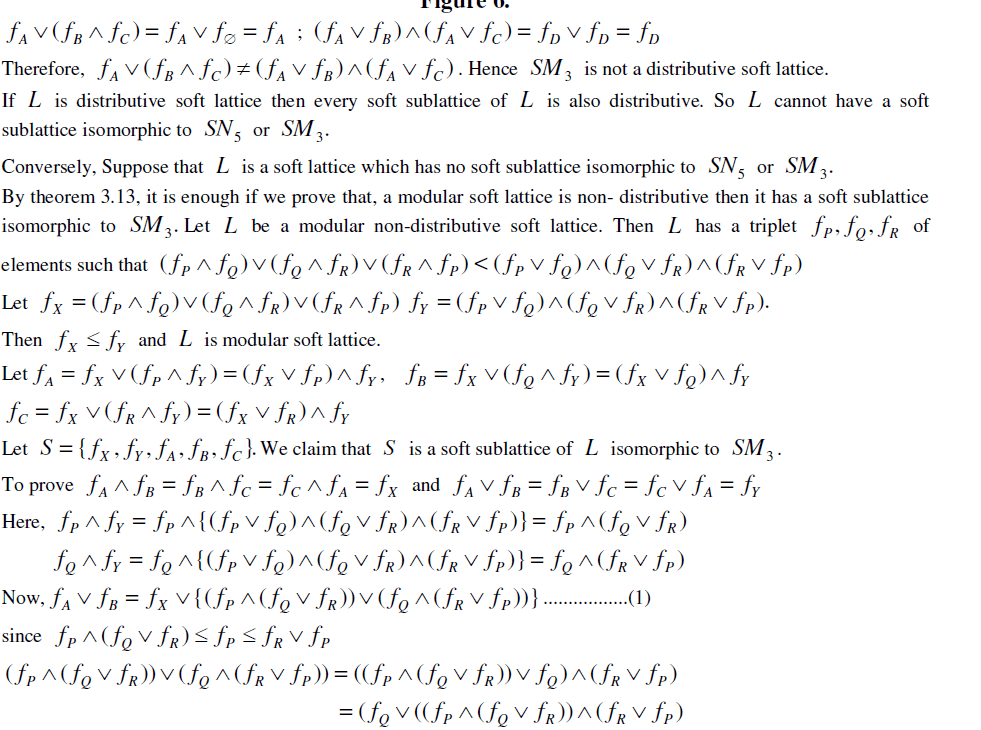image
image
image
image
image

CONCLUSION
In this paper, we have given characterization theorems for modular soft lattices and distributive soft lattices.We are studying about these soft lattices and are expected to give some more results.

References
  1. Cagman N., and Enginoglu S., Soft set theory and uni-int decision making, Eur. J. Oper. Res. 207/2 (2010), 848-855.
  2. Davey B.A., and Priestley H.A. Introduction to lattices and order, Cambridge University Press, India, 2009.
  3. Gabor Szasz, Introduction to Lattice Theory, Academic Press, New York and London, 1963.
  4. George Gratzer, General Lattice Theory, Second edition, Birkhauser verlag, Boston, 1998.
  5. Irfan Ali M., Feng Feng, Xiaoyan Liu, Won Keun Min and Shabir M., On some new operations in soft set theory, Comput. Math. Appl. 57 (2009), 1547-1553.
  6. Karaaslan F., Cagman N., and Enginoglu S., Soft Lattices, J. New. Res. Sci. 1 (2012),5-17.
  7. Li F., Soft Lattices, Glob. J. Sci. Front. Res.10/4 (2010), 56-58.
  8. Maji P.K., Biswas R., and Roy A.R. Soft set theory, Comput. Math. Appl. 45 (2003) 555-562.
  9. Molodtsov D.A., Soft set theory-First Results, Comput. Math. Appl. 37 (1999) 19-31.
  10. Nagarajan E.K.R., and Meenambigai G., An Application of Soft Sets to Soft Lattices, Kragujevac J. Math. 35/1 (2011), 75-87.