ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
M. Janaki1, Dr. M. Ganaga Durga2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Currently Cloud computing technology have attracted more and more people to store their private data on third-party servers either for ease of sharing or for cost saving. When people enjoy the advantages of these new technologies and services bring about, their concerns about data security also arise. Naturally, people would like to make their private data only accessible to authorized users. When a user wants to run an application in the cloud, the user is required to provide a digital identity. Just as handwritten signatures or physical thumbprints are commonly used to uniquely identify people for legal proceedings or transactions, so digital signatures are commonly used to identify electronic entities for online transactions. Data encryption using asymmetric keys is an expensive operation directly proportional to the size of the data being encrypted; it potentially doubles the size of the data increasing the processing power and bandwidth required to process and transfers the data which increases the transmission cost. In this paper, we propose a JKG Digital Signature algorithm which is a less expensive than public key encryption to provide security in the cloud. By implementing the Algorithm in MATLAB 7.1 the signed file size is calculated. When it is compared with encrypted file size it is proved that signed file size is less, which in turn decreases the cost requirements. We can implement the proposed algorithm to enhance the privacy in cloud since it provides authentication, integrity and non-repudiation altogether.
Keywords |
| Cloud computing, Security issues, Identity management, Encryption, Public Key encryption algorithm, Digital Signature. |
INTRODUCTION |
| Cloud computing, as an emerging computing paradigm, enables users to remotely store their data in a cloud, so as to enjoy services on-demand [3]. Migrating data from the user side to the cloud offers great convenience to users, since they can access data in the cloud anytime and anywhere, using any device, without caring about the capital investment to deploy the hardware infrastructures. Especially for small and medium-sized enterprises with limited budgets, they can achieve cost savings and the flexibility to scale (or shrink) investments on-demand, by using cloud-based services to manage projects, enterprisewide contacts and schedules [1]. |
| We can easily foresee that these security concerns and requirements would become more urgent in the coming era of cloud computing wherein individuals, organizations, and businesses may outsource their various types of data, including the highly sensitive data, into the cloud [6]. A digital signature is a mathematical scheme that is used to authenticate the sender of an electronic document. It ensures that the document is really from the sender and not from someone else while at the same time ensuring that the message that reaches the recipient is the same one sent without any alterations. Digital signatures are very efficient in legally binding documents because they are difficult to imitate and can be time-stamped. In this paper we explore a feasible solution based on a novel digital signature method which is proposed as a new algorithm to reduce the transmission cost. |
RELATED WORK |
| Patrick J. Flinn and James M. Jordan have explained the usage of their algorithm for encryption and digital signatures. "Public key cryptography," a method for encrypting messages to be transmitted over an insecure channel, and "digital signatures," a method for authenticating the author of a message transmitted over an insecure channel, are emerging as fundamental tools for conducting business securely over the Internet[13]. In this paper, working principle of RSA algorithm is described with the modular arithmetic also known as clock arithmetic. |
ORGANISATION |
| The rest of this paper is organized as follows. In Section 2, we introduce the preliminary concepts such as cloud computing, encryption and digital signature. In Section 3, we define the principle of JKG encryption algorithm. In Section 4, we describe the proposed JKG digital signature algorithm and analyze its performance with examples and simulated results in the form of tables and graphs. Finally we conclude the paper in Section 5.The future research direction is given in Section 6. |
PRELIMINARIES |
| In this section the concepts regarding cloud computing, security issues, identity management, encryption, and digital signature are explained. |
CLOUD COMPUTING PARADIGM |
| Cloud Computing is a new computing model that distributes the computing missions on a resource pool that includes a large amount of computing resources [7]. As the result of development of the service models, infrastructure as a service (IAAS), platform as a service (PAAS), and software as a service (SAAS) cloud becomes more prevalent. |
| There are mainly three types of clouds: private clouds, public clouds and hybrid clouds. To ensure adequate security in cloud computing, various security issues, such as backup, data security, data locality, data integrity, data segregation, data access, data confidentiality, identity management and sign-on process, network security, all need to be taken into account [5]. Identity management (IdM) or ID management is a broad administrative area that deals with identifying individuals in a system and controlling the access to the resources in that system by placing restrictions on the established identities [8]. |
ENCRYPTION METHODOLOGY |
| Encryption is a method of hiding data so that it cannot be read by anyone who does not know the key. The key is used to lock and unlock data [4]. To encrypt a data one would perform some mathematical functions on the data and the result of these functions would produce some output that makes the data look like garbage to anyone who doesn't know how to reverse the operations [14]. Encryption can be used to encrypt files that the owner feels are too sensitive for anyone else to read. |
| Private Key means that the same method is used to encrypt and decrypt. If someone knows what method was used to encrypt the message then that person can decrypt the message. Private Key encryption has the benefits of being very fast. A disadvantage to private key cryptography is that the key must be communicated beforehand. Public key cryptography is also known as asymmetric cryptography which was created to eliminate the shortcomings of private key cryptography [11]. The biggest advantage of public key cryptography is that no prior communication needs to take place between the recipient and the sender. Public key cryptography works like this, everyone has two keys, a public key, which the entire world has access to, and a private key, which only the owner knows[2]. |
DIMENSIONS OF DIGITAL SIGNATURE |
| A digital signature uniquely identifies the originator of digitally signed data and also ensures the integrity of the signed data against tampering or corruption. One possible method for creating a digital signature is for the originator of data to create the signature by encrypting all of the data with the originator's private key and enclosing the signature with the original data. Anyone with the originator's public key can decrypt the signature and compare the decrypted message to the original message. Because only someone with the private key can create the signature, the integrity of the message is verified when the decrypted message matches the original. If an intruder alters the original message during transit, the intruder cannot also create a new valid signature. If an intruder alters the signature during transit, the signature does not verify properly and is invalid. The framework of digital signature is shown in Figure1. |
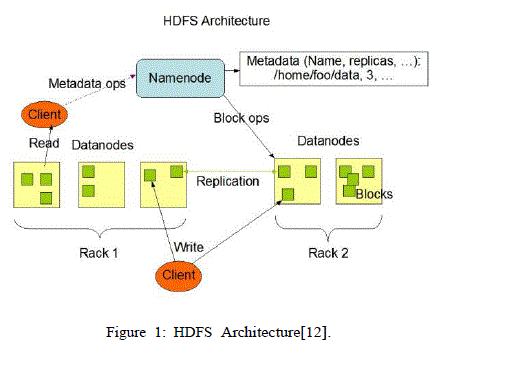 |
| created by signing message digests with the originator's private key to create a digital thumbprint of the data. Because only the message digest is signed, the signature is usually much shorter than the data that was signed [13]. Therefore, digital signatures place a relatively low load on computer processors during the signing process, consume insignificant amounts of bandwidth, and produce small amounts of cipher text for cryptanalysis. |
JKG ENCRYPTION ALGORITHM |
| The JKG encryption algorithm is a public-key encryption algorithm in which two keys such as one public key and one secret key generated. The public key is used to encrypt the messages and known to all, but those who knew the secret key or the private key can only decrypt the message. So this proposed algorithm enjoys the benefit of public key cryptography i.e. increased security and convenience. The main disadvantage of JKG encryption algorithm is the encrypted file size which is twice the input file size. We can overcome this disadvantage in the proposed JKG digital signature algorithm by using the hash technique. |
PROPOSED SYSTEM |
| In our paper, we propose a new digital signature algorithm in which two keys such as one public key and one secret key are generated. The public key is used to verify the signature and known to all, but those who knew the secret key or the private key can only generate the signature. The main disadvantage of existing encryption algorithm is more file size. We can overcome this disadvantage in the proposed digital signature algorithm by using the hash technique for reducing the file size. One of the main motivations for identity management in cloud computing is to enable different services reuse user profile information [16]. Such user profile information can be safeguarded with the proposed algorithm with a minimum cost which enhances cloud privacy. |
PROPOSED JKG DIGITAL SIGNATURE ALGORITHM |
| The proposed algorithm is a digital signature algorithm in which two keys such as one public key and one secret key generated. The private key of the originator is used as input to the algorithm which transforms the data being signed (or its hash value). This transformation can only be reversed, and the data decrypted and accessed, by use of the originator’s public key, which is provided to the recipient(s) by the originator. |
| The main disadvantage of JKG encryption algorithm is its doubled file size. We can overcome this disadvantage in the proposed JKG digital signature algorithm by using the hash technique. The process flow of JKG digital signature algorithm is shown in Figure2. the private key of the originator to produce the digital signature. Having calculated the message digest this can be encrypted using the private key of the originator to produce the digital signature. |
 |
| The proposed JKG digital signature algorithm contains three steps. In the first step the public key and the private key are generated. The second step has the formula to generate the signature and the third step contains the process of verifying the signature. |
| Anyone with the public key can use it to perform a validity check of digital signatures created by the private key. Only a digital signature created by the appropriate private key decrypts and validates properly with the public key. If a different private key was used to sign the data, the validity check fails. If the contents of digitally signed data or the digital signature have been tampered with or are corrupted, the validity check also fails. |
 |
| Valid digital signatures can be used to perform the following functions: Authenticate online entities, Verify the authorship or origin of digital data, ensure the integrity of digital data against tampering. |
MATHEMATICAL MODELLING |
| The mathematical model for our proposed algorithm is given in this section. The first part contains Poisson distribution along with its graph. The second part contains the queuing model. |
POISSON DISTRIBUTION |
| In statistics, Poisson distribution is one of the discrete probability distribution. Our JKG digital signature algorithm contain discrete input so this distribution can be used for modeling our proposed algorithm by calculating the possibilities for number of bytes signed within the given average execution time (λ). A Poisson random variable (n) refers to the file size. Applying the formula of Poisson distribution JKG digital signature algorithm is obtained as, |
 |
| Where a is the average execution time and b is the file size and e is the base of logarithm (e=2.718). The Poisson graph drawn for our proposed JKG digital signature algorithm is shown in Figure3. |
 |
| 124 bytes and average execution time λ = 9.476 ms which is calculated after implementing the proposed JKG digital signature algorithm for various input file with different sizes. |
QUEUING MODEL |
| The M/M/1 queue model is suitable for network concepts, which means {infinity/infinity/FCFS} system. In this mode, the arrivals and departures are a Poisson distribution with a single server, infinite queue length, calling population infinite and the queue discipline is FCFS. This is the simplest queue system that can be studied mathematically. This queue system is also simply referred to as the M/M/1 queue. |
| This queue model when applied to our proposed algorithm, it assumes that the number of bytes encrypted within a given interval of time W, follows a Poisson distribution, with parameter λ. This parameter λ is the average number of bytes encrypted in time t which is also the variance of the distribution. The queuing formula is L = λW, where L is the large quantity of executed file (it is the product of average of encrypted bytes and time interval). The M/M/1 queue model is applicable to our proposed JKG encryption algorithm. |
ANALYSIS OF JKG DIGITAL SIGNATURE ALGORITHM |
| The proposed JKG digital signature algorithm is analyzed with tabulated results after implementation and bar charts are drawn based on the data obtained. |
| The JKG encryption algorithm is implemented and the time taken for encryption and decryption of various input files with different sizes (43 bytes, 77 bytes, 124 bytes, 265 bytes, and 512 bytes) is tabulated in TABLE1. |
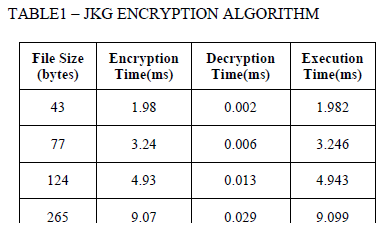 |
| The TABLE1 contains four fields, first field is the file size of five input files taken into consideration, second field is the time taken for encrypting the files, third field is the time taken for decrypting the files, the last field is the execution time i.e. the total time taken for encryption and decryption. From the above table the average execution time for JKG encryption algorithm is observed as 7.2408ms. |
| The JKG digital signature algorithm is implemented and the time taken for sign generation and sign verification of various input files with different sizes (43 bytes, 77 bytes, 124 bytes, 265 bytes, and 512 bytes) is tabulated in TABLE2. |
 |
| The TABLE2 contains four fields, first field is the file size of five input files taken into consideration, second field is the time taken for generating the sign, third field is the time taken for verifying the sign, the last field is the Signature time i.e. the total time taken for sign generation and sign verification. From the above table the average execution time for JKG digital signature algorithm is observed as 9.476 ms. |
| The JKG encryption algorithm is implemented and the time taken for encryption of various input files with different sizes (43 bytes, 77 bytes, 124 bytes, 265 bytes, and 512 bytes) is found and the data is plotted in the bar graph as shown in Figure4. |
 |
| The Figure4 shows the JKG Encryption graph with the file size (bytes) in the x-axis and encryption time (ms) in the y-axis. The five magenta bars in the bar graph shows the encryption time taken for each file mentioned above. |
| The JKG encryption algorithm is implemented and the time taken for decryption of various input files with different sizes (43 bytes, 77 bytes, 124 bytes, 265 bytes, and 512 bytes) is found and the data is plotted in the bar graph as shown in Figure5. |
 |
| The JKG digital signature algorithm is implemented and the time taken for signature generation of various input files with different sizes (43 bytes, 77 bytes, 124 bytes, 265 bytes, and 512 bytes) is found and the data is plotted in the bar graph as shown in Figure6. |
 |
| Fig.6. JKG Signature Generation Graph |
| The Figure6 shows the JKG signature generation graph with the file size (bytes) in the x-axis and generation time (ms) in the y-axis. The five green bars in the bar graph shows the signature generation time taken for each file mentioned above. |
| The JKG digital signature algorithm is implemented and the time taken for signature verification of various input files with different sizes (43 bytes, 77 bytes, 124 bytes, 265 bytes, and 512 bytes) is found and the data is plotted in the bar graph as shown in Figure7. |
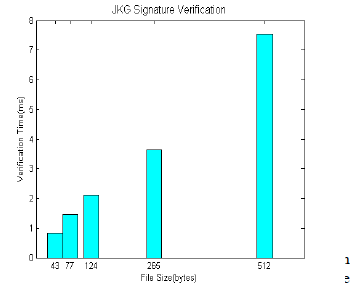 |
| (ms) in the y-axis. The five cyan bars in the bar graph shows the signature verification time taken for each file mentioned above |
SIMULATION OF JKG DIGITAL SIGNATURE ALGORITHM |
| The proposed JKG digital signature algorithm is implemented in MATLAB 7.1. Five input files with different sizes (43 bytes, 77 bytes, 124 bytes, 265 bytes, and 512 bytes) are taken into consideration. These files are signed using our JKG signature generation program and time taken for signing and output file size is found. Then the signed files are verified using our JKG signature verification program. |
WORKING PRINCIPLE |
| For showing the working principle of JKG digital signature algorithm the input file3 which is having the Tender details of a company named Paul Constructions is taken. Tender details of a company are sensitive information that is to be signed electronically before sending it through the net. The signed result is shown below |
 |
| p = d94d889e88853dd89769a18015a0a2e6b |
| q= b9cfde843176b88741d68cf096952e950813151058 r = 10001 |
| s = 0xb5 0xe6 0x25 0x03 0x2e 0x91 0x88 0xdf 0xb4 0xe1 0x82 0xd8 0x99 0x17 0xa2 0xc4 0x3d 0xd9 0xbb 0x84 0xb1 0xd9 0x86 0x8c 0xf0 0x02 0x7d 0xcc 0xbf 0x63 0xa1 0xde 0x1c 0x46 0x0f 0xab 0xcc 0xbb 0xfa 0xfe 0xdb 0x2d 0x8d 0xbc 0x51 0x0d 0xc2 0x0b 0x65 0x68 0x64 0x7b 0xfe 0x3e 0x0e 0xa6 0x30 0x5e 0x33 0x15 0xd6 0x5a 0x15 0x62 0xc2 0xd6 0x16 0x23 0x3a 0x08 0x06 0x17 0x79 0xe8 0xb5 0xb1 0x94 0x7a 0x39 0xe6 0xe6 0xcd 0x91 0x04 0x43 0x3b 0xe6 0xd7 0x92 0x36 0x74 0x73 0xb9 0x82 0xef 0xa0 0x3c 0x7f 0xa1 0x00 0x42 0x3d 0x15 0xe1 0x87 0xe5 0x5b 0xee 0xd2 0xd4 0xe4 0xef 0xff 0xac 0xff 0x3d 0x32 0x50 0x04 0xfb 0x92 0x1b 0x01 0x1a 0x69 0x88 0xc0 0x48 |
| Where m is the original message given by the user, p is the public key known to all which is used to verify the signature, q is the secret key generated which is known to only those who is going to generate the signature, r is the public modulus used for generating both public key and the secret key, s is the signature generated. |
| After the results of both JKG encryption algorithm and JKG digital signature algorithm are simulated, the time taken for executing (encryption + decryption) various files with different sizes (43 bytes, 77 bytes, 124 bytes, 265 bytes, and 512 bytes) are compared in TABLE3. |
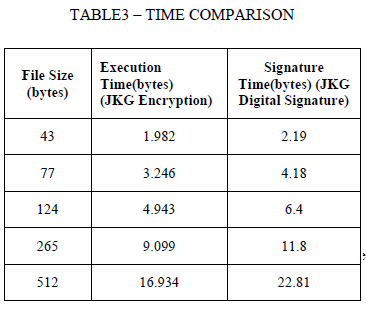 |
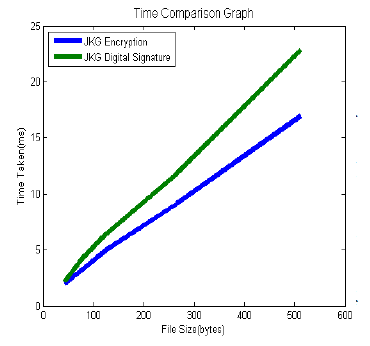
| size of five input files taken into consideration, second field is the time taken for executing the files using JKG encryption algorithm, third field is the time taken for signing the files using JKG digital signature algorithm. We can plot the data in the comparison table TABLE3 in the form of a line graph which is shown in the Figure8. bytes, and 512 bytes) is compared in TABLE4 |
 |
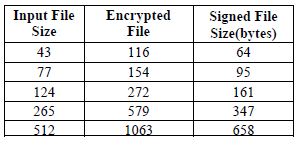 |
| The TABLE4 contains three fields, first field is the file size of five input files taken into consideration, second field is the size of the encrypted file executed using JKG encryption algorithm, third field is the size of the signed file generated using JKG digital signature algorithm. |
| We can plot the data in the comparison table TABLE4 in the form of a bar graph which is shown in the Figure9. |
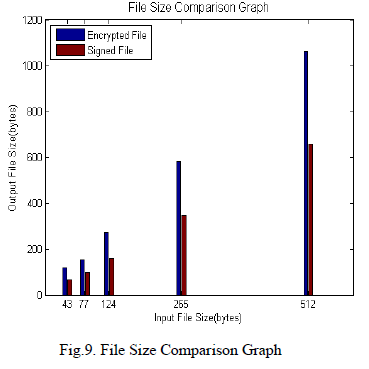 |
| The Figure9 shows the file size comparison graph of JKG encryption and JKG digital signature algorithms with the input file size (bytes) in the x-axis and output file size (bytes) in the y-axis. The blue bar in the graph shows the encrypted file size and green bar in the graph shows the signed file size of each input file mentioned above. |
| The average encrypted file size is 436.8 bytes and average signed file size is 265 bytes. The comparison of two values shows that the signed file size 40% less than the encrypted file size. When the size of the data becomes less, it decreases the processing power and bandwidth required to process and transfers the data which decreases the transmission cost. Hence it is proved that the proposed JKG digital signature algorithm is cheaper than JKG encryption algorithm. |
CONCLUSION |
| Apart from the benefits offered by cloud computing, it also brings some security problems to Internet users. Public key Encryption algorithm will be suitable for encoding and decoding sensitive information in the cloud, but a digital signature uniquely identifies the originator of digitally signed data and also ensures the integrity of the signed data against tampering or corruption. Existing Public key encryption algorithm ensures only the data security and not concentrating on authentication or integrity. In this paper, we have proposed a JKG Digital Signature algorithm which ensures authentication, integrity and non-repudiation. It is also proved that JKG digital encryption is cheaper than JKG encryption which shows that the JKG Digital Signature algorithm will enhance the cloud privacy at a minimum cost by using it with Identity management. |
FUTURE DIRECTION |
| Presently the majority of cloud computing systems provide digital identity for users to access their services. Identity-based cryptography has some attraction characteristics that seem to fit well for digital identities. Hence in future Identity based cryptography may be used with digital signature to provide cloud security. |
ACKNOWLEDGEMENT |
| The Authors express their sincere thanks to the Principals and Management of Dr.Umayal Ramanathan College for women, Karaikudi, and Government Arts College for women, Sivaganga, for their co-operation and constant encouragement. |
References |
|