ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Deepa M1, Dr.T.V.U.Kirankumar2, Muthukumaran S3, Mohankumar C4
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This paper presents, for the first time, a combined blur deconvolution and edge-directed interpolator based on adaptive gradient angle interpolation locally defined, straight line approximations of image isophotes for super resolution. The proposed blur estimation process is supported by an edge-emphasizing smoothing operation, which improves the quality of blur estimates by enhancing strong soft edges toward step edges, while filtering out weak structures. For better performance, the blur estimation is done in the filter domain rather than the pixel domain using the gradients of the Low Resolution and High Resolution images. The proposed method can accommodate arbitrary scaling factors, provides state-of-the-art results in terms of PSNR as well as other quantitative visual quality metrics, and has the advantage of reduced computational complexity that is directly proportional to the number of pixels..
Keywords |
| LR (Low resolution), HR (High resolution), MIDB (Multi-image Deblurring), SIDB (Single-image Deblurring), SR (super resolution) |
INTRODUCTION |
| Capturing high-quality images and videos is critical in many applications such as medical imaging, astronomy, surveillance, and remote sensing. Traditional high-resolution (HR) imaging systems require high-cost and bulky optical elements whose physical sizes dictate the light-gathering capability and the resolving power of the imaging system, a constraint that has persisted since their invention [1][2] .In contrast; computational imaging systems combine the power of digital processing with data gathered from optical elements to generate HR images. Artefacts such as aliasing, blurring, and noise may affect the spatial resolution of an imaging system, which is defined as the finest detail that can be visually resolved in the captured images. Blur deconvolution (BD) and super-resolution (SR) are two groups of techniques to increase the apparent resolution of the imaging system. One major difference between these two groups is that the goal in a BD problem is just to undo blurring and noise, whereas SR also removes or reduces the effect of aliasing. As a result, the input and output images in BD are of the same size, while in SR the output image is larger than the input image(s). The other difference is that since severe blurs eliminate or attenuate aliasing in the underlying low-resolution (LR) images, the blur in a SR problem may not be as extensive as in a BD problem. In image resolution limits the extent to which zooming enhances clarity, restricts the quality of digital photograph enlargements, and, in the context of medical images, can prevent a correct diagnosis. this paper is literature is composed as blur deconvolution from the paper[21] and the interpolation approach non-linear algorithms frequently result in better visual and quantitative performance than fixed-kernel approaches [22].Single image interpolation (zooming, upsampling, or resizing) can artificially increase image resolution for viewing or printing, but is generally limited in terms of enhancing image clarity or revealing higher frequency content. Interpolators based on approximations of the ideal sinc kernel (pixel replication, bilinear, bicubic, and higher-order splines) are commonly used for their flexibility and speed; however, these approaches frequently contribute to blurring, ringing artefacts, jagged edges, and unnatural representation of isophotes (curves of constant intensity) in processed images. Results can be improved somewhat by tailoring the sinc-approximating kernel to suit the image being interpolated and non-linear algorithms frequently result in better visual and quantitative performance than fixed-kernel approaches. These papers can be classified into two main categories: methods that consider blur identification and image restoration as two disjointed processes [11], [13], [14], [15], and methods that combine these two processes into a combined procedure, e.g. interpolation(SAGA) [16], [18]–[20]. For both BD and SR, techniques are proposed in the literature for reconstruction from a single image or multiple Images. Methods reconstructs one HR image by fusing from multiple edge-directed interpolator. By contrast, superresolution (SR) methods, which are also known as learning-based, patch-based or example-based SR techniques, are proposed in which small spatial patches within the input LR image are replaced by similar higher resolution patches previously extracted from a number of HR images. |
PROPOSED SYSTEM |
| A. Blind Estimation |
| Blind deconvolution is the problem of recovering a sharp version of an input blurry image when the blur kernel is unknown. Mathematically, we wish to decompose a blurred image y as |
| where x is a visually plausible sharp image, and k is a non negative blur kernel, whose support is small compared to the image size. This problem is severely ill-posed and there is an infinite set of pairs (x, k) explaining any observed y. For example, One undesirable solution that perfectly satisfies is the no-blur explanation: k is the delta (identity) kernel and x = y. The ill-posed nature of the problem implies that additional assumptions on x or k must be introduced. Blind deconvolution is the subject of numerous papers in the signal and image processing. Despite the exhaustive research, results on real world images are rarely produced. Recent algorithms have proposed to address the ill-posedness of blind deconvolution by characterizing x using natural image statistics. While this principle has lead to tremendous progress, the results are still far from perfect. |
| The linear forward imaging model in the spatial domain which illustrates the process of generating the kth LR image gk(x↓, y↓; c) of size Ng x × Ng y ×C from a HR image f (x, y; c) of size N f x × N f y × C is defined |
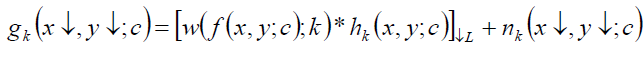 |
| Here, (x↓, y↓) and (x, y) are the position of pixels within the LR and HR image planes, respectively, Nx and Ny are the number of pixels in x and y spatial directions, respectively, N is the total number of LR images, C is the number of colour channels, and * is 2D convolution operator. In w(·) is the warping function according to a global/local parametric/ nonparametric motion model, hk is the kth PSF caused by the overall blur of the system originated from different sources (such as optical lens, sensor, motion, depth of scene, etc.), and nk is the noise which is commonly modelled as AWGN. Also [·]↓L is the downsampling operator called SR downsampling factor or SR scale ratio (depending on the point of view) so that N f x = LNg x and N f y = LNg y . According to, the original HR image is warped, convolved with the overall system PSF, down sampled by the value of L, and finally corrupted by noise to generate each LR image. |
 |
| Blind deconvolution algorithms exhibit some common building principles, and vary in others. proposed a unified method for blind BD and SR in which the well-known TV regularization is used as the image prior and the following regularization for the blurs: |
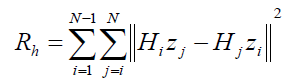 |
| Where zj is the LR image gi up sampled to the size of HR image f, i.e. zi = DT gi . A TV regularization term is also added to Rh with a very small coefficient, the role of which is just to diminish noise in the estimated PSFs. The form of regularization (but without pre-up sampling of LR images) is first proposed in for the blind MIBD problem. By rearranging Rh, it can be written as Rh = ||Nh|| where h =[hT 1 , . . . , hT n ]T and N is a matrix solely based on the LR images which will contain the correct PSFs in its null space, i.e. Nh = 0 only if h contains the correct PSFs. While this prior is able to properly estimate the HR image even when the LR images have different blurs, the estimated PSFs are with some inevitable ambiguity Even if the PSFs are the same; this ambiguity will still exist in the estimated PSFs. By contrast, in our proposed method which is introduced in Section III, there is no such ambiguity in estimating the blurs since our method is intrinsically designed for the case that all PSFs are equal. Another work on blind SR using the MAP framework is suggested in which the cost function for estimating the HR image includes a TV prior. The blur identification process consists of three optimization steps: first, initial estimates of the blurs h0 are obtained using the GMRF prior’s ||Eh||2, where E is the convolution kernel of Laplacian mask. Second, parametric blur functions b that best fit the initial blur estimates are calculated. Third, final estimates of the blurs h are obtained by reinforcement learning toward the parametric estimates using the quadratic prior ||h-b||2. The most important limitation of this work is that considering just a few parametric models does not cope with the diversity of blur functions in reality. Also in this work, the estimated blurs are not demonstrated and the reported PSNR values for the estimated HR images are low (less than 18 dB). |
| B. Fixed Kernel, Preliminary Interpolation |
| It is shown for the first time in that, in a blind image deconvolution problem, more accurate estimation for the blur (and subsequently for the image) can be obtained if in the blur estimation process, the estimated image f is preprocessed by an edge-emphasizing smoothing operation. This has a positive effect on the quality of the blur estimate from the following aspects: |
| 1) Blur(s) can be estimated best from salient edges and their adjacent pixels, so by smoothing f weak edges and also false edges caused by ringing are smoothed out and do not contribute to the blur estimation; |
| 2) Noise has a stronger adverse effect in non-edge regions than in edge regions, so smoothing the non-edge regions helps in improving the blur estimation; |
| 3) Ground-truth images are assumed to have sharp and binary-like edges; therefore, replacing soft edges with step edges in f provides a closer estimate of the ground-truth image and assists in getting better blur estimation, especially in the initial steps of the blind optimization where the estimated image f is still quite blurry. |
| To smooth out non-edge regions and improve the sharpness of edges, in the shock filtering operation of is used by which a ramp edge gradually approaches a step edge through a few iterations. Since the performance of the shock filtering and some other edge-emphasizing smoothing techniques are influenced by noise, in some works the image is pre-smoothed. |
| C.Segment Adaptive Gradient Angle Interpolation |
| The first step of SAGA interpolation is to identify the vector of parameters (α or β) that best maps a line of N pixels to intensity-matched pixels in adjacent lines (i.e., the α or β values that best satisfy. As established in the previous section, the displacements for a given pixel are influenced by the pixels in a surrounding neighbourhood. Specifically, we introduce a stiffness parameter k such that elements in α or β are linearly related over segments of k +1pixels. The α and β values are explicitly computed at the end points of each segment or “nodes” and interpolated for intermediate locations. |
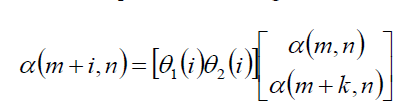 |
| Where pixel locations [m, n] and [m + k, n] are considered nodes and the inter-nodal pixel displacements are interpolated for 0 < i < k. In Eq. (14), θ1 and θ2 are the linear basis functions: θ1(i ) = k−I k and θ2(i ) = ik , for 0 < i < k. Determinations of α for other rows are independent repetitions of the same process that can be run in parallel. The algorithm for determining β for a column comprises a straightforward change of variables or, alternatively, the image matrix can be transposed and the procedure can be repeated as described. |
RESULTS |
 |
| The Right row of images shows the enlargement results for a two-times down-sampled version of the Lena image the enlargement results for a region of the original Barbara test image The SAGA result shows a lesser degree of jaggedness and some thinning. The SME result shows neither issue in the knee area; however, along the bottom side of the pant leg, there is significant cross-hatching observable. Moderate artificial texture is also present in the arm region of all of the output images. |
CONCLUSION |
| The proposed blur estimation procedure pre-processes the estimated HR image by applying an edge emphasizing smoothing operation which enhances the soft edges toward step edges while smoothing out weak structures of the image. Segment Adaptive Gradient Angle (SAGA) interpolation. The algorithm operates at a low computational cost. In addition to having low raw computational complexity, the SAGA algorithm is easily configured for parallelization as data can be independently processed one line at a time. Beyond addressing the classic problem of resizing greyscale images by factors of two with accuracy and speed, the algorithm is also well suited for dynamic zooming applications. Displacements need only be calculated for an image once, and can then be applied to interpolate the image to any new size. Given the ever increasing range of image viewing devices and consumer expectations for interactivity, this feature is viewed as an important benefit of SAGA interpolation. |
References |
|