ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
S. K. Tiwari1, R. P. Dubey2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In This paper, we generalize and obtain common fixed point theorems for a pair of mappings satisfying generalized multi-valued type contractive condition in the setting of cone metric spaces with normal constant 1.Our results generalize the recent results of varies authors
Keywords |
| Cone metric spaces, common fixed point, multi-valued mapping, contractive Condition, normal cone. |
I. INTRODUCTION |
| In 1970, Covitz Nadler’s (see [6]) gave the following results “Multi-valued contraction mappings generalized metric spaces” using this result. H. E. Kunze et, al (see [3]) introduce an iterative method involving projections that guarantees convergence, from any starting point to a point the set of all fixed points of a multifunction operator T. The results [3] were generalized by Dubey [16]. Especially, Nadler’s. Jr. [7] gave a generalization of Banach’s contraction principle to the case of set-valued maps in metric spaces. Recently, Huang and Zhang [1] introduced the concept of cone metric space by replacing the set of real numbers by an ordered Banach space and obtain some fixed point theorems for mappings satisfying different contractive conditions. Subsequently, the results [1] were generalized and studied the existence of common fixed points of a pair of self mappings satisfying a contractive type condition in the frame work of normal cone metric spaces, see for instance [2], [4], [5],[9] and [11]. The authors [10, 14] introduced the concept of multi-valued contractions in cone metric spaces and using the notion of normal cones, obtained fixed point theorems for such mappings. As we know, most of known cones are normal with normal constant . Further, the author [12] and [13] proved two results, fixed points and common fixed points of multifunction on cone metric spaces. These results also generalized by Dubey and Narayan [17].In this paper, we prove common fixed point theorems for pair of multi-valued maps in cone metric spaces with normal constant K=1, which generalize and extend the results of [1], [8] and [15]. |
II. PRELIMINARY NOTES |
 |
 |
 |
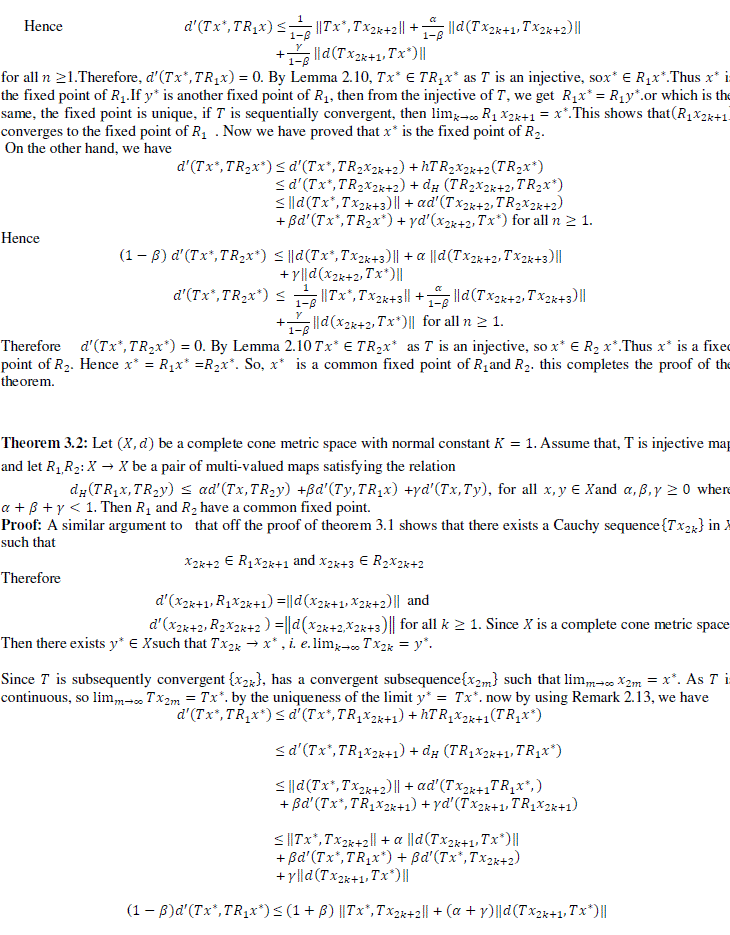 |
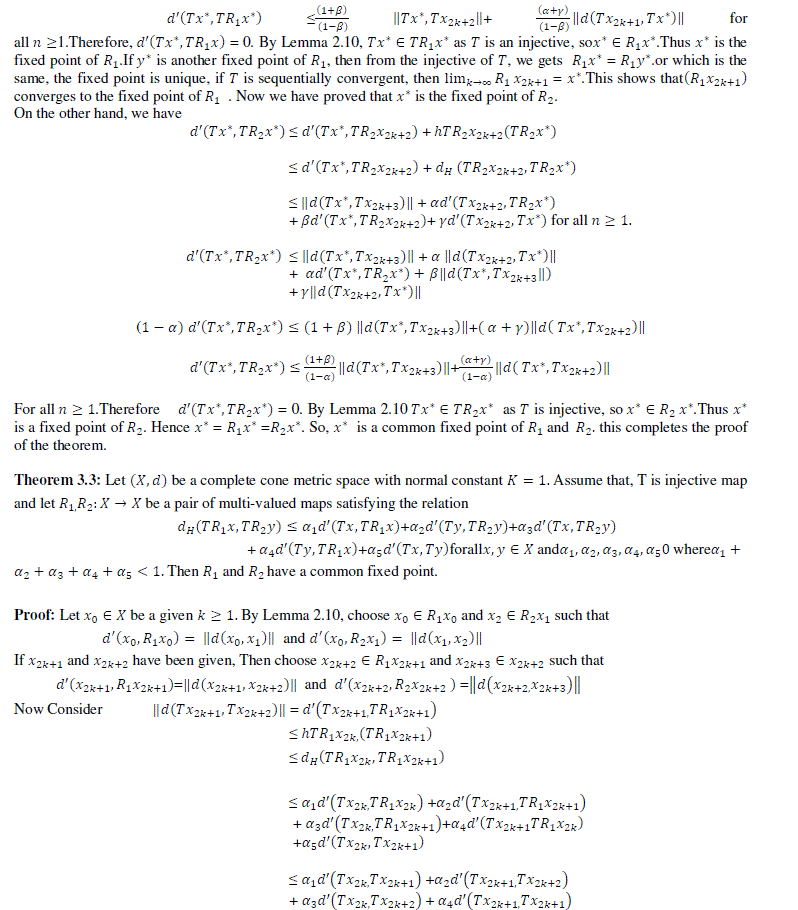 |
 |
 |
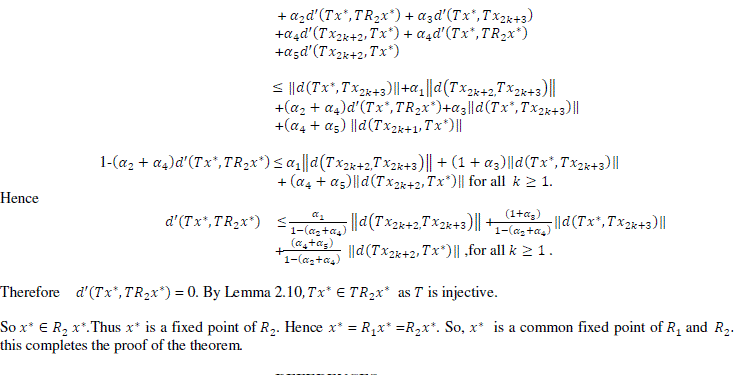 |
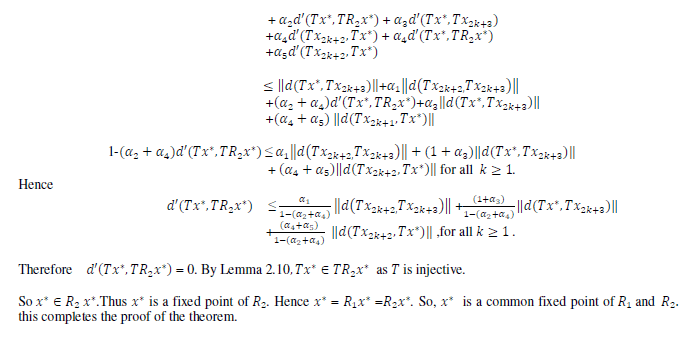 |
References |
|