International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

COMMON FIXED POINT THEOREMS FOR SIX SELF MAPS UNDER SUB COMPATIBLE AND SUB SEQUENTIALLY CONTINUOUS MAPS IN FUZZY METRIC SPACES BY USING IMPLICIT RELATION

M. Rangamma 2 , G. Mallikarjun Reddy1 , P. Srikanth Rao 3
  1. Assistant professor, Department of Mathematics, CVR Engineering College, Ibrahimpatan, Hyderabad, India
  2. Professor, Department of Mathematics, O.U., Hyderabad, India
  3. Professor, Department of Mathematics, B.V.Raju Engineering College, Narsapur, Hyderabad, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The purpose of this paper is to prove common fixed point theorems for the new concepts of sub compatibility and sub sequential continuity in fuzzy metric spaces using Implicit Relation for six self mappings which are weaker than occasionally weak compatibility and reciprocal continuity. In general all known results on commuting, weakly commuting, compatible, weak compatible, semi compatible and occasionally weak compatible maps in fuzzy metric spaces are generalized in this note.

Keywords
Compatible maps, R-weakly commuting maps, Weakly compatible maps, Sub compatible maps, Sub sequentially continuous maps.

INTRODUCTION
In 1965, the concept of fuzzy sets was introduced by Zadeh[1] which laid the foundation of fuzzy mathematics. Kramosil and Michalek [2] introduced the notion of a fuzzy metric space by generalizing the concept of the probabilistic metric space to the fuzzy situation. George and Veeramani [3] modified the concept of fuzzy metric spaces introduced by Kramosil and Michalek [2]. There are many view points of the notion of the metric space in fuzzy topology for instance one can refer to Kaleva and Seikkala [4], Kramosil and Michalek [2], George and Veeramani [3]. Popa ([5]-[6]) introduced the idea of implicit function to prove a common fixed point theorem in metric spaces. Singh and Jain [7] further extended the result of Popa ([5]-[6]) fuzzy metric spaces. Using the concept of R-weak commutative mappings, R.Vasuki [8] proved the fixed point theorems for Fuzzy metric space. Recently in 2009, using the concept of sub compatible maps, H.Bouhadjera et. al. [9] proved common fixed point theorems. In 2010 and 2011, B.Singh et. al. [7] proved fixed point theorems in Fuzzy metric space and Menger space using the concept of semi-compatibility, weak compatibility and compatibility of type (β) respectively. In this paper, we prove fixed point theorems by using concepts of sub compatibility and sub sequential continuity which are respectively weaker than occasionally weak compatibility and reciprocal continuity in Fuzzy metric space using Implicit Relations. With them, we establish a common fixed point theorem for six maps, which extends the results of Kamal Wadhwa.et al.[10] and others.

II. PRELIMINARIES
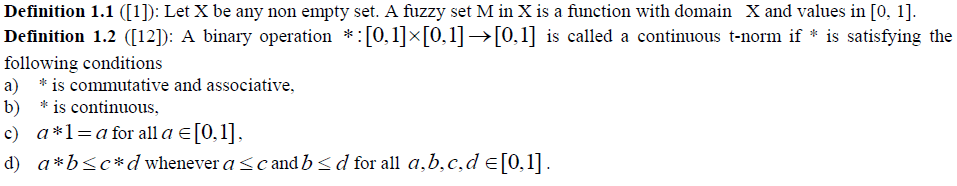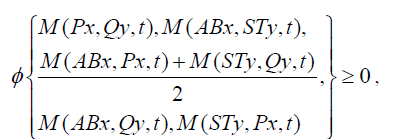image
image
image
image
image
image
image
image
then P, Q, S, T, A and B have a unique common fixed point. Now replacing self maps by the identity maps in theorem 2.6 we get the particular cases for four, three and two self mappings which generalizes the results of Kamal Wadhwa et al.[10] and others.

IV.CONCLUSION
This article investigates common fixed point theorems for six self mappings. The concept of sub compatible maps and sub sequentially continuous maps in Fuzzy metric spaces using implicit relations has also been used. Several Fixed point theorems in Fuzzy metric spaces such as fixed point theorems for four, three and two self mappings have been derived in the present study as particular cases.

References
  1. Zadeh, L. A., “Information and Control”, Fuzzy Sets, No.8, pp.338-353, 1965.
  2. Kramosil, I., Michalek, J., “Fuzzy metric and statistical metric spaces”, Kybernetica, No.11, pp.336-344, 1975.
  3. George, A., Veeramani, P., “On some results in fuzzy metric spaces”, Fuzzy Sets and Systems, No.64, pp.395-399, 1994.
  4. Kaleva, O., Seikkala, S., ”On fuzzy metric spaces”, Fuzzy Sets Systems, No.12, pp.215-229, 1984.
  5. Popa, V., “A general coincidence theorem for compatible multi valued mappings satisfying an implicit relation”, Demonsratio Math., No.33, pp.159- 164, 2000.
  6. Popa, V., “Some fixed point theorems for compatible mappings satisfying on implicit relation”, Demonsratio Math., No.32, pp.157 – 163, 1999.
  7. Singh, B., Jain, A., and Lodha, B., “On common fixed point theorems for semi compatible mappings in Menger space”, Commentationes Mathematicae, 50 (2), pp.127-139, 2010.
  8. Singh, B., Jain, A., and Masoodi, A. A., “Semi-compatibility, weak compatibility and fixed point theorem in fuzzy metric space”, International Mathematical Forum, 5(61), pp.3041-3051, 2010.
  9. Vasuki, R., “Common fixed points for R-weakly commuting maps in fuzzy metric spaces”, Indian J.Pure.Appl.Math. No. 30 pp.419-423, 1999.
  10. Kamal Wadhwa, Farhan Beg and Hariom Dubay, “Common Fixed Point Theorem for sub compatible and sub sequentially continuous maps in fuzzy metric space using implicit relation” , IJRRAS, 9(1), pp.87-92, 2011.
  11. Kutukcu, S., Sharma, S., and Tokgoz, H., “A fixed point theorem in fuzzy metric spaces”, Int.J.Math.Analysis, 1(18), pp.861-872, 2007.
  12. Klement, E. P., Mesiar R., and Pap, E., “Triangular Norm”, Kluwer Academic Publishers, Dordrecht., In Trends in Logic, vol.8, 2000.
  13. Grabiec, M., “Fixed points in fuzzy metric spaces”, Fuzzy Sets and Systems, No.27, pp.385-399, 1988.
  14. Pant, R. P., Common fixed points of four mappings, Bull.Cal.Math.Soc., No.90, pp.281- 286, 1998.
  15. Pant, R. P., Jha, K., “A remark on Common fixed points of four mappings in a fuzzy metric space”, J.FuzzyMath.12(2), pp.433-437, 2004.
  16. Bouhadjera, H., and Godet-Thobie, C., “Common fixed point theorems for pairs of sub compatible maps”, arXiv:0906.3159v1 [math.FA] 17 June 2009.
  17. Cho, Y. J., Pathak, H. K., Kang, S.M., and Jung, J.S., “Common fixed points of compatible maps of type (β) on fuzzy metric spaces”, Fuzzy Sets and Systems, No.93, pp.99-111, 1998.
  18. Balasubramaniam, P., MuraliSankar, S., and Pant, R. P., “Common fixed points of four mappings in a fuzzy metric space”, J.Fuzzy Math. 10(2), pp.379-384, 2002.
  19. Sharma, S., Deshpande, B., “Compatible multi valued mappings satisfying an implicit relation”, Southeast Asian .Bull.Math. No.30, pp.535-540, 2006.
  20. Jungck, G., “Compatible mappings and common fixed points (2)”, Internat.J.Math. Math. Sci, pp.285- 288, 1988.
  21. Sharma, S., “Common fixed point theorems in fuzzy metric spaces”, Fuzzy Sets and Systems No.127, pp.345-352, 2002.
  22. Sharma, S., Deshpande, B., “Discontinuity and weak compatibility in fixed point consideration on non-complete fuzzy metric Spaces”, J.Fuzzy Math.11(2), pp.671-686, 2003.
  23. Jungck, G., and Rhodes, B.E., “Fixed point for occasionally weakly compatible mappings”, Fixed point theory 7(2), pp.287- 296, 2006.
  24. Al-Thagafi, M. A., Naseer Shahzad, “Generalized I-Non expansive self maps and invariant approximation”, Acta Mathematica sinica, English Series 24(5), pp.867-876, 2008.
  25. Al-Thagafi, M. A., and Naseer Shahzad, “A note on occasionally weakly compatible maps”, Int.J. Math. Anal. 3(2), pp.55-58, 2009.
  26. Alamgir Khan, M., Sumitra,”Sub Compatible and Sub Sequentially Continuous Maps in Fuzzy Metric Spaces”, Applied Mathematical Sciences., 29(5), pp.1421-1430, 2011.