ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Prajakta N. Badhe1, Mohd. Zain Kangda2, Shobha G. Kundu3, Abdul Ashfak Khan4
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In open channel flow measurement, weirs and flumes are used to produce known repeatable characteristics in the process of stream. Weirs, flumes and other devices develop a liquid head that is used to measure the flow rate. Weirs also give engineers as well as hydrologist a simple method of measuring the rate of fluid flow in small and medium sized stream or in industrial discharge locations. One such type of the parabolic weir is studied here. In this type of weir the discharge equation was having a flow depth exponent as a whole number. A Parabolic weir profile gave the simplified discharge equation with two as the flow depth exponent. In this project the parabolic weir with weir angles 30°, 45°, 60° were designed and fabricated. Various head measurements are taken in the flume at various equidistant places. The coefficients of discharge were measured
Keywords |
| Parabolic weir, Weir angle, Coefficient of discharge |
INTRODUCTION |
| Water flowing in open channels serves humans in many ways and accurate record of discharge is crucial in each of such uses. Floods cause such extensive damage that records of extreme events are needed for the design of flood control reservoirs, flood warning systems, flood plane declination, bridges and culverts. To measure the discharge in an open channel, field methodologies and laboratory methodologies are available. |
| Efficient use of water for irrigation depends largely on measurement of water. Principles and methods of water measurement can be understood well by knowing the increasing utilization and value of available water and the growing tendency among irrigation companies to base annual water charges on the volume of water used. Information concerning the relations between water, soils and plants cannot be utilized in irrigation practice without the measurement of water. |
Weirs |
| A weir is a device which is used to measure the rate of flow of a liquid through a small channel. Weirs have been studied extensively and are applied as water control structures and flow measurement devices in a wide range of agriculture and municipal applications. |
Classification of weirs |
| Weirs are classified according to the shape of the opening, shape of crest, effect of the sides of the nappe and nature of discharge. The important classification of weirs is as follows: |
| a) According to shape of the opening weirs are classified as: |
| 1) Rectangular weir |
| 2) Triangular weir |
| 3) Trapezoidal weir |
| 4) Parabolic weir |
| b) According to the shape of crest weirs are classified as: |
| 1) Sharp crested weir |
| 2) Broad-crested weir |
| 3) Narrow-crested weir |
| 4) Ogee-shaped weir |
| c) According to the effect of sides on the emerging nappe weirs are classified as: |
| 1) Weirs with end contraction |
| 2) Weirs without end contraction |
| The sharp-crested weir, being a simple device, is most commonly used in channels for flow measurement and flow regulation. Attempts have been made to study in detail the flow over different shapes of normal conventional weirs, side weirs, oblique weirs and parabolic weirs. Most of the investigators have expressed the discharge coefficient as a function of various parameters. |
Parabolic weir and its advantages |
| Parabolic weir is a special type of weir which governs the flow depth exponent as two. Parabolic weirs are governs the merits of rectangular weirs as well as that of triangular weirs. The main advantage of this weir is that the expression for discharge contains flow depth exponent as two which makes the manual calculations very simple. The discharge capacity of parabolic weirs is 33.3% more as compared to that of triangular weirs under similar flow velocity and weir dimensions. Since the parabolic shape is closer to a triangular shape than a rectangular shape, the parabolic weirs are expected to hold the accuracy and sensitivity as that of standard triangular weirs. The hydraulic performance of parabolic weir will have the combined merits of both rectangular and triangular weirs as its profile is considered as an intermediate profile. The designed parabolic weirs after calibration can be readily employed as simple, efficient field irrigation and industrial flow measurement devices based on the dimensions of the existing channels and the required discharge capacity. |
BASIC CONCEPT OF PARABOLIC WEIR |
Theoretical discharge of the parabolic weir designated by weir angles |
 |
| The sketch of a parabolic weir profile as shown in figure-2.1, has H and L as the total height and projected length of weir profile respectively; h is the head steady flow depth from the bottom of weir; l is chord length at an arbitrary depth; z is the arbitrary depth of liquid above weir bottom; x and y the horizontal and vertical coordinates of weir profile and Ø is the weir angle. The total theoretical discharge across parabolic weir is obtained by integrating the fluid velocity over the area of flow based on continuity equation. |
 |
| Where, K is the weir geometry constant in ms-1 and is specific to different parabolic weir profiles (H and Ø). Theoretical discharge Eq. (2.1.10) was determined for various values of h, after obtaining the weir geometry constant K Eq. (2.1.11) from the fabricated weir dimensions. The theoretical discharge is greater than the actual discharge due to contraction and friction. The actual discharge relationship was obtained from the theoretical discharge using Eq. (2.1.10) after evaluating the coefficient of discharge which is given by equation 2.1.12. |
 |
 |
 |
| Based on the x & y co-ordinates obtained analytically which are shown in table 3.1, a smooth weir curve was obtained for the weir angle Ø=30° (figure-3.1.1). Similarly, figure-3.1.2 and figure-3.1.3 shows the smooth parabolic curve for weir angles Ø=45° and Ø=60° respectively. |
 |
| From the above figures (figure-3.1.1, figure-3.1.2 & figure-3.1.3) it can be seen that the width of the weir with weir angle Ø=60° is greater as compared to that of weir angle Ø=30° and Ø=45°. As the weir angle is increasing, the weir width also increases. All these parabolic weir profiles (figure-3.1.1, figure-3.1.2 & figure-3.1.3) were used to find the actual discharge Qa. |
Actual and Theoretical discharge characteristics of parabolic weir |
| Theoretical discharge was proportional to flow depth and was observed to be always greater than actual discharge. Theoretical discharge is greater than actual discharge values of simplifying assumptions that do not consider friction, velocity of approach & end contractions. Table 3.2.1 and 3.2.2 show the coefficient of discharge for weir angle 60o using actual discharge and comparison of actual discharge and theoretical discharge respectively. |
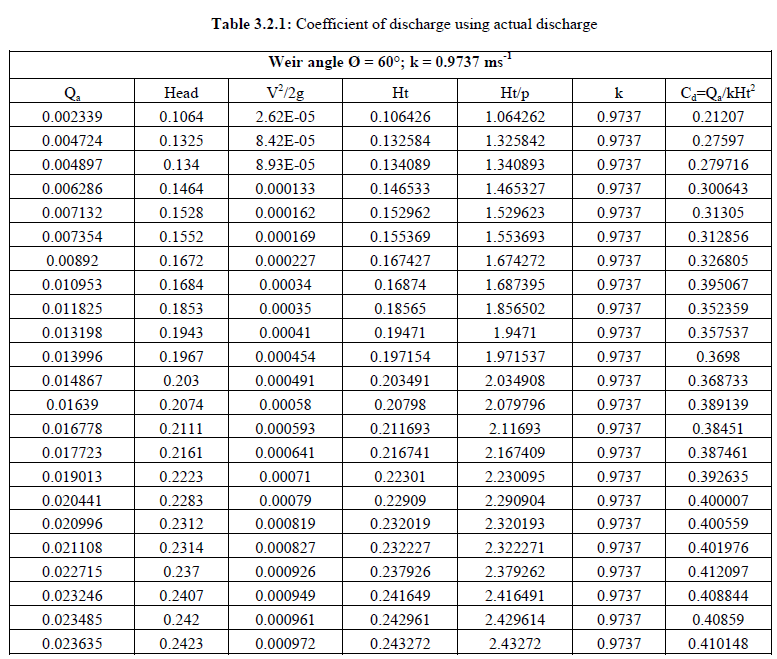 |
| The above table shows the calculations for coefficient of discharge which was obtained from the actual discharge. It can be noted that as the actual discharge is increasing, the coefficient of discharge also increases. Figure 3.2.1 shows the variation of crest coefficient which is obtained by plotting the graph between head to weir height (Ht/p) and coefficient of discharge. |
 |
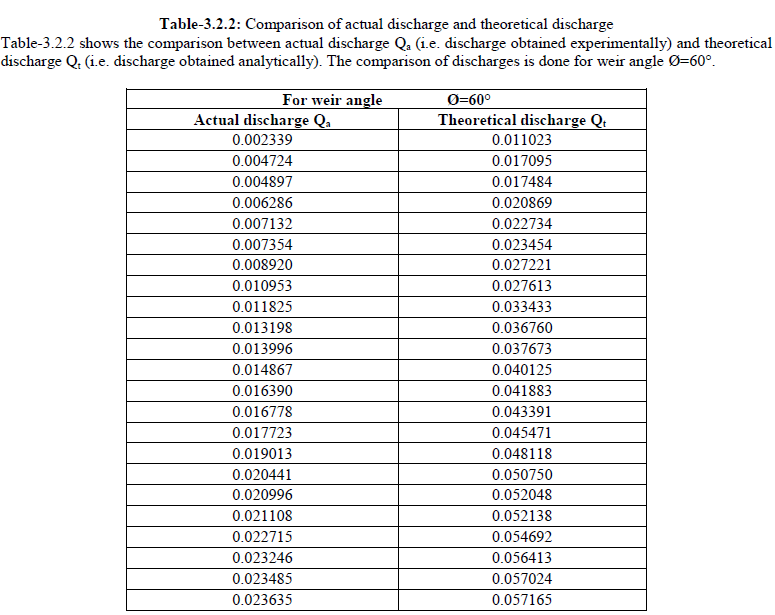 |
| From the above table, a comparative graph (figure-3.2.2) has been plotted between actual discharge and theoretical discharge for weir angle Ø=60°. It can be seen that a straight graph profile is obtained by plotting actual discharge on xaxis and theoretical discharge on y-axis. |
 |
CONCLUSIONS |
| The major conclusions drawn from present study are as follows: |
| 1. The shape of weir profile to produce a simplified discharge equation, with two as the exponent of flow depth, was derived as a parabola. |
| Qt = K h2 |
| 2. A relationship for obtaining a parabolic weir profile for fabrication as a function of weir angle was obtained. |
| 3. The equations for the weir constants, along with the discharge models, can be applied to determine the actual discharge characteristics of studied weir angles and range of flow depths, as well as predict the discharge characteristics of weirs at any intermediate angle. |
| 4. Discharge capacity of similarity dimensioned rectangular, triangular, and parabolic weirs can be compared theoretically from the flow areas as discharge is proportional to flow area. Considering weirs having total crest length L and maximum depth H, based on the area of different weir profiles, the parabolic weir covers 66.66% of rectangular weir flow area, whereas the triangular weir covers only 50.0%. This means that parabolic weir will have 33.3% more discharge capacity than triangular weirs, under similar flow velocity and weir dimensions. Since the parabolic shape is closer to a triangular shape than a rectangular shape, the parabolic weirs are also closer to have the accuracy and sensitivity of standard triangular weirs. A parabolic profile being the intermediate shape, its hydraulic performance will have the combined merits of both rectangular and triangular weirs. Based on the dimensions of existing channels and the discharge capacity required, the designed parabolic weir after calibration can be readily employed as simple and efficient field irrigation and industrial flow measurement devices. |
| As the parabolic weirs have the combined merits, such as the increased discharge capacity of rectangular weirs and the sensitivity of triangular weirs, along with the simplified discharge equation, they find application in automated flow control systems, field irrigation, and industrial flow measurements. |
References |
|