ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
F.R. Castillo-Soria1, I. Algredo-Badillo1, S. Sánchez-Sanchez2, M. A. Castillo-Soria3, S.Juárez-Vázquez1
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In many digital signal processing (DSP) applications, it is required to increase the number of samples that a discrete time signal contains; this process is called interpolation and it implies an estimation of the values to be inserted. In this work, a comparative analysis of the digital interpolation process for diverse techniques of insertion and FIR filtering is presented. The aim is to obtain the best reconstruction of a test signal which has been designed to be a simple model of a real signal. First, decimation is used up to the limit of the Nyquist theorem in order to generate the test signal. Then, this signal is fed into the interpolator, passing through two stages: 1) sample insertion, which is based on zero stuffing, zero-order hold and splines, and 2) filtering, which is based on two FIR techniques, such as time convolution and fast filtering using DFT. The results show that by using the zero stuffing technique together with the fast filtering, a despicable reconstruction error is obtained. In addition, this arrangement has the advantage of a fast response.
Keywords |
| Interpolation filter, sample insertion, signal reconstruction, spline, zero stuffing, zero-order hold |
I. INTRODUCTION |
| It is known that human beings have been using interpolation since the Second Century A.D. [1]. At the present time, there are diverse techniques that can be utilized for signal reconstruction. Some of the more commonly used techniques are: cubic, Lagrange, splines, Hermite and statistical interpolation [2, 3]. In the world of the digital signal processing, the technique used is the so called digital interpolation (DSP interpolation)[4, 5].In digital signal processing, it is sometimes required to vary the sampling rate, for example, when information is shared between two processors which are working at different sampling rates, when scaling is applied to an image and to simplify a system in order to improve the information transmission speed [6, 7]. The decimation process can be defined as decreasing the sampling rate by extracting samples of a signal (usually D is defined as the decimation order). If it is required to increase the sampling rate, the interpolation process is implemented (usually M is defined as interpolation order), which implies an estimation of the values of the added samples [8]. |
| In general, it is important to highlight that decimation can cause the loss of information. Furthermore, if an interpolation is used, the designer will always try to get the best approximation to the original signal. In the process of digital interpolation two stages are defined [9]: 1) insertion of samples to increase the sampling rate, and 2) filtering the signal to eliminate the undesirable spectral components, originating the effect of a smooth signal in the time domain. In this way, the effectiveness of the interpolation depends on the insertion technique as well as on the filter [10, 11]. |
| In [12], a way to derive the best sample points is proposed; however, these results are not optimal in any sense. More recently, in [13], analytical results of interpolation process are presented specifically for Lagrange-Hermite polynomials. |
| In [14], digital interpolation systems consideringan integer upsampling are presented, here, implementation issues arediscussed for different types of filters however the insertion techniques are not analyzed. |
| In this work, the digital interpolation process is analyzedconsidering different insertion techniques. As a test bed, it is proposed to use a signal that has a uniform content of low frequencies. This original signal is transformed to the time domain by using the Inverse Discrete Fourier Transform (IDFT), and then the signal is decimated taking into account the Nyquist theorem, see Fig. 1. The signal fed to the interpolator is composed of 16 samples from the original 160 (using a decimation with D=10). In the stage of the sample insertion, three techniques have been selected for comparative analysis. These techniques have been chosen to cover a wide range of insertion techniques. |
| The first is a classic technique called zero stuffing, which consists of insertion of zeros in the places where the signal would have a value. The second is the zero-order hold, which holds the current level of the signal; it better approximates the time domain signal. The third is a more complex insertion technique, a smooth interpolation using spline method, which at this stage approximates the original signal the best possible way in the time domain. |
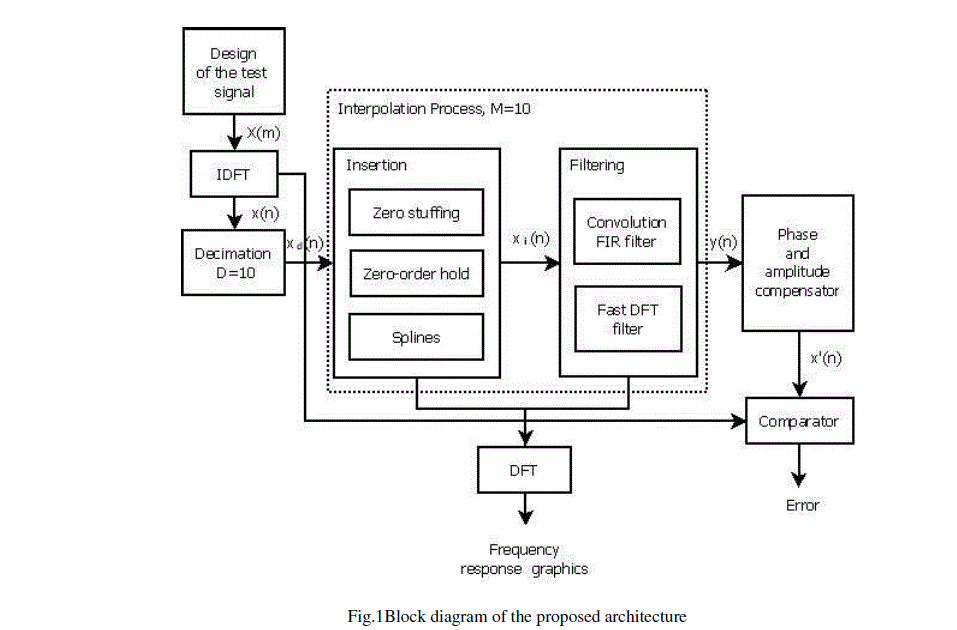 |
| In the filtering stage, the signals with insertion of samples are fed into the low-pass digital filters. Two types of FIR (Finite Impulse Response) filters are implemented: i) a classic filter by mean of convolution in the time domain and ii) a fast filtering using the DFT. In the filter’s outputs, the interpolated or reconstructed signals are obtained. |
| The error is measured in the last module. The result is obtained by comparing processed signals against the original signal without decimation. A comparison of the processing time is also presented. Results are based on simulations in the programming language MATLAB. |
II. DESIGN OF THE LOW-PASS TEST SIGNAL |
| The test signal has been designed to contain a constant level of low frequencies and a transition region as shown in Fig. 2. After that, the IDFT is used in order to obtain the desired signal in the time domain. This signal is selected with 160 samples and oversampled. If a resolution in frequency of 1 KHz is considered, the cut-off frequency has a value of 16 KHz / 2 = 8 KHz, and the original sampling rate is 160 KHz. At the Nyquist rate limit, the sampling rate is reduced to fs = 16Ksamples/second. According to the sampling theorem, this is the lowest sampling rate which will still permit adequate reconstruction of the original signal [15]. |
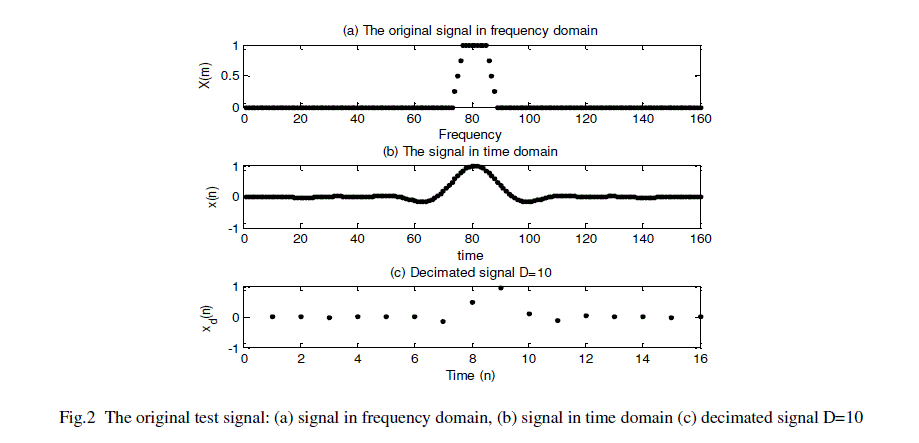 |
 |
III. SAMPLE INSERTION |
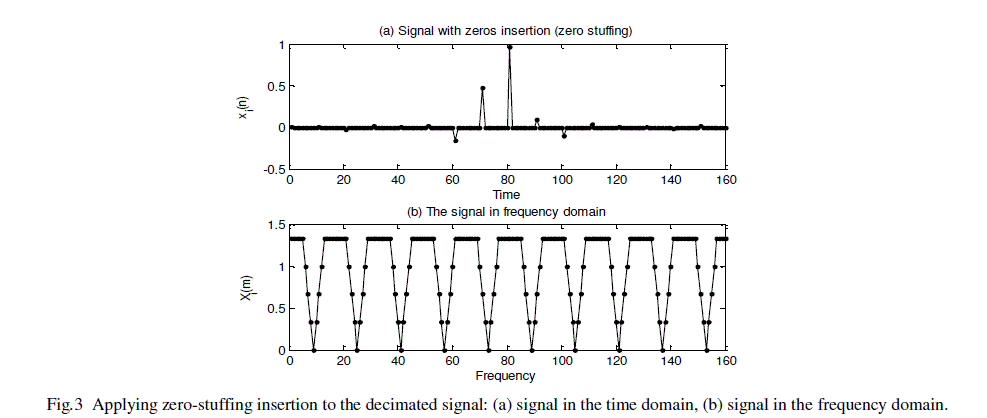
| The process of sample insertion is applied to the decimated signal using the three techniques previously mentioned: zero stuffing, zero-order hold and spline interpolation. Fig. 3-5 show the signals modified by the sample insertion techniques. These signals will be applied to the second stage. Additionally, the DFT, see Eq. 3, is used to obtain their spectral characteristic in the frequency domain. |
| For a given signal x(n), the DFT in exponential form is described by Eq. 3. |
 |
| A. Zero Stuffing |
| Using an interpolation order of M=10, the inserted signal with zero stuffing has 160 samples, see Fig. 3a. Its DFT is shown in Fig. 3b. The effect of the zero stuffing occurs in the frequency domain as separated replicas fs Hz (16 samples). However the same form of the original signal is obtained in each replica (image). |
 |
| B. Zero-order hold |
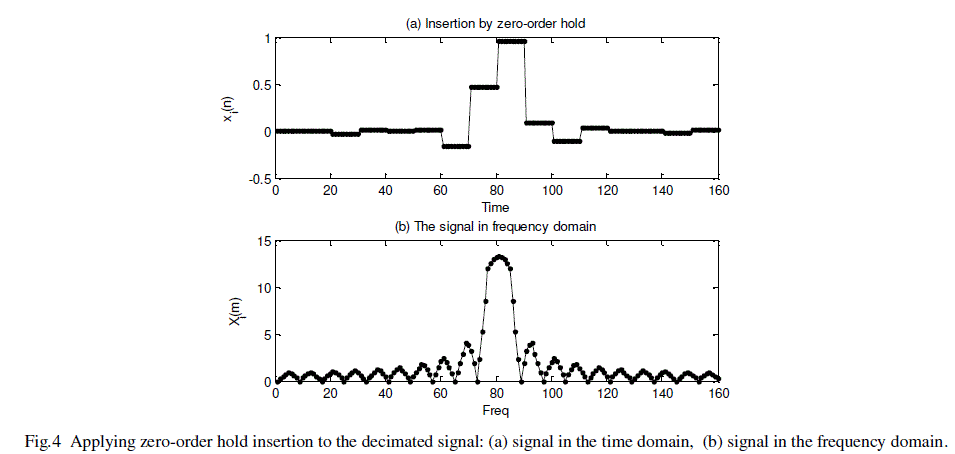
| Using zero-order hold insertion technique, the generated signal better approximates to the original signal when it is compared (in this intermediate point) against the signal with zero stuffing. In the frequency domain, it has attenuated amplitude of the high-frequency components (images), see Fig.4b, however spectral components are modified in the pass-band in comparison to the original signal. |
 |
| C. Spline Interpolation |
| Performing spline insertion, the signal presents a waveform that better approximates to the original signal, when it is compared against zero stuffing and zero-order hold. In the frequency domain, as shown in Fig. 5b, the images are attenuated and the passband is slightly modified. |
 |
| Each insertion technique affects the passband in different way. The three types of insertion present small variations to each other, see Fig. 3b, 4b and 5b. |
| D. Convolution FIR filter |
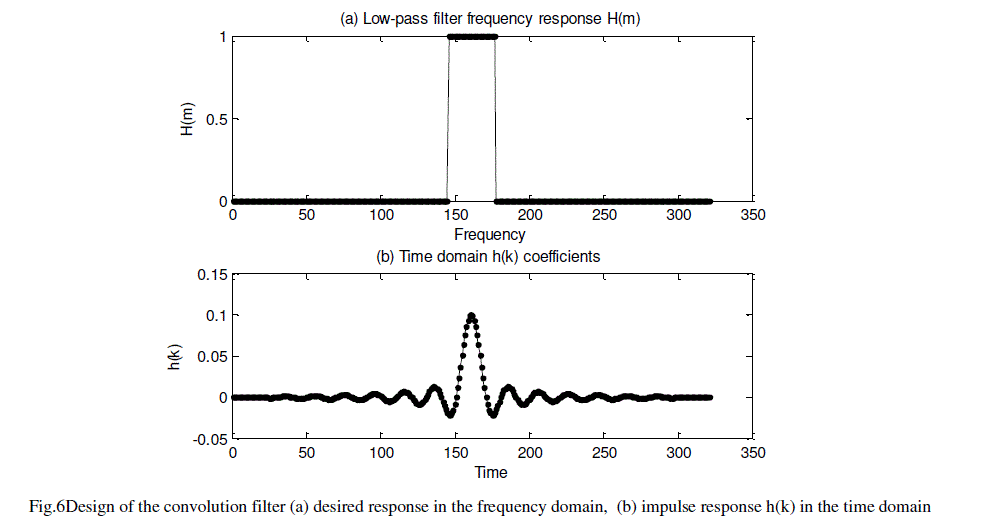
| To design the FIR filter impulse response h(k), first the filter response is proposed in the frequency domain. Next, IDFT is applied to obtain h(k). Additionally, a small adjustment is required to centerh(k) to the origin. The low pass filter has 320 taps and the cut-off frequency is 8 kHz. This design allows the low-pass signals and rejects the highfrequency components added in the insertion of samples, see Fig. 6. |
| Applying the IDFT to H(m), it is possible to obtain the impulse response h(k) of the filter, see Eq. 4. If the pulse is centred in the origin, the result has only real components. |
 |
| Where: |
| K: amount of samples with unitary amplitude of the frequency signal H(m). |
| m,k: indexes for the frequency and time, respectively. |
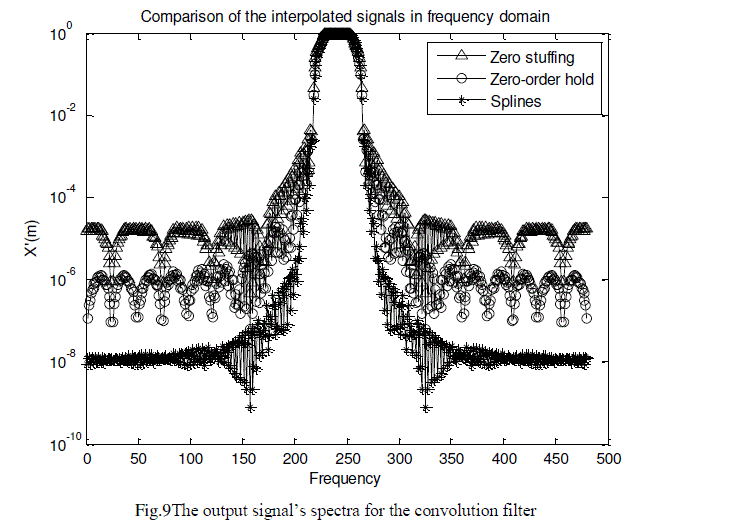
| The peak amplitude is computed with Eq. 5. |
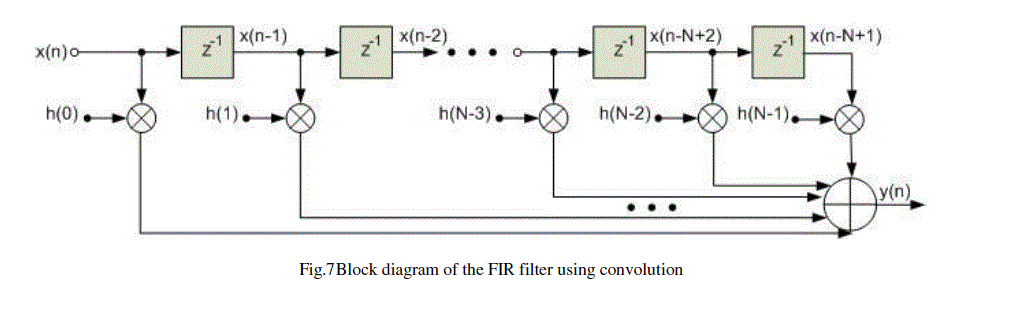 |
| The architecture used for the filter by convolution is shown in Fig. 7; this filter operates the data h(k), generating y(n) that is determined by the convolution function, see Eq. 6. |
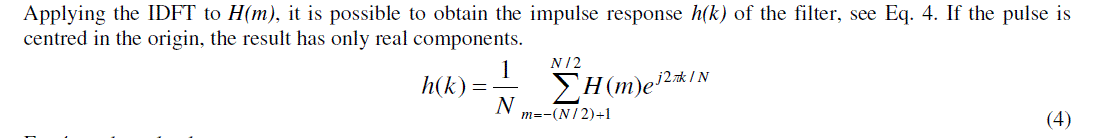 |
 |
| The signals y(n) generated by the FIR filter are normalized and set in phase before comparisons. Fig. 8 shows a comparison of output signals, considering the original signal x(n). |
 |
| As a measurement of the error, a definition of the average sample error is used, see Eq. 7. |
 |
| Table 1 shows results for each of the sample insertion methods and the FIR filter using convolution of 320 taps. |
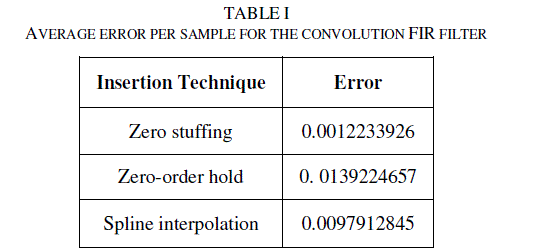 |
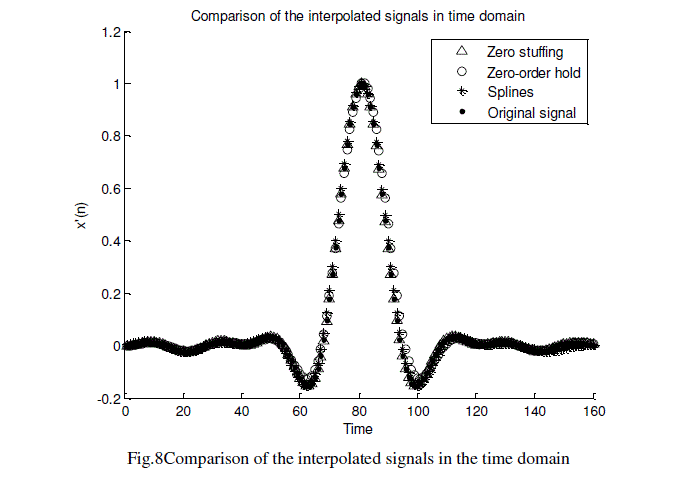
| In Fig. 9, frequency components of the FIR filter output signals before being trimmed are shown. It can be observed in the highest frequencies that the interpolated signal using splines presents the greater attenuation, whereas the signal with zero stuffing has significant components in the high frequencies. The signal inserted by the zero-order hold technique appears in the middle. |
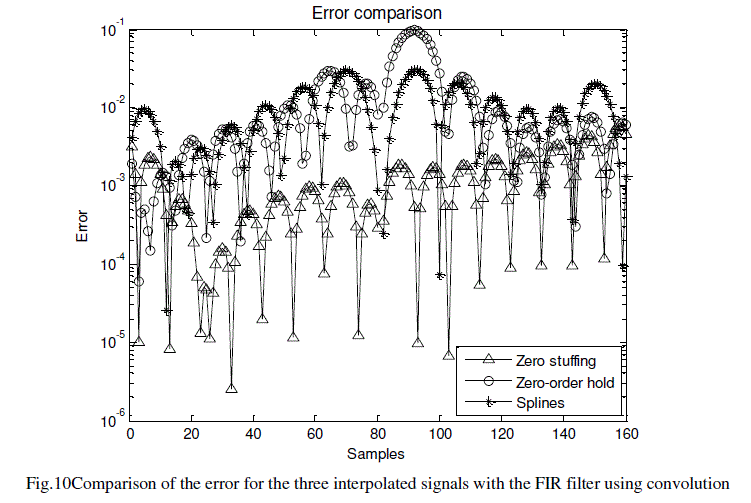 |
| In Fig. 10, the measured error for the comparator is shown. It is presented for each of the signals interpolated through filtering by convolution. In order to compare it to the original signal, the output signals of the filter have been trimmed to 160 samples. |
 |
| The program was carried out on a personal computer with a 3 GHz Pentium IV processor. On average, the time needed for the convolution filter process was 99.4908 ms. |
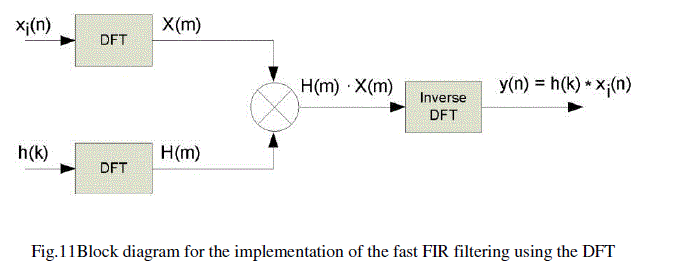
IV.FAST FIR FILTERING USING DFT |
| Since the convolution in the time domain corresponds to multiplication in the frequency domain, the scheme shown in the Fig. 11 can be used to realize the filtering. First, the spectra of the signals are obtained, which is reached by using the DFT for both the input signal xi(n) and the filter response h(k). Next, the multiplication is realized in the frequency domain and then, the IDFT is applied to return to the time domain, obtaining y(n). In several studies, it is demonstrated that these filters are faster than the filters that use convolution, whenever the output sequence size is greater than 30 [8]. |
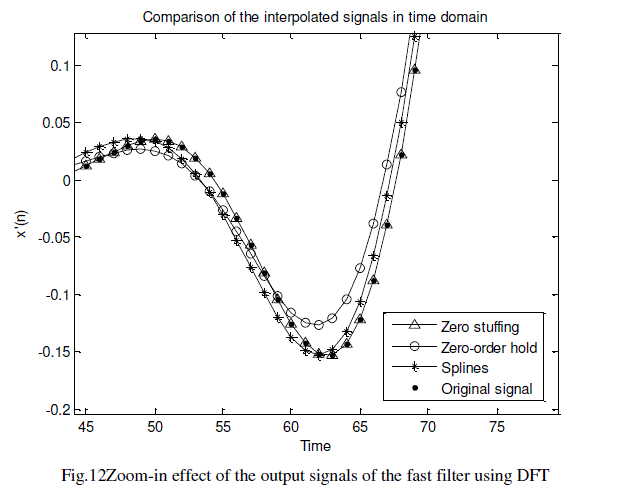 |
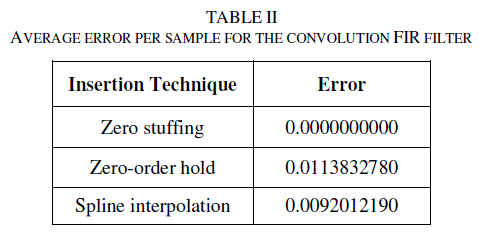
| Applying a zoom-in from samples 45 to 75, see Fig. 12, the original signal appears within the triangle that represents the signal with zero stuffing. The measured error represented as the magnitude of the difference between the values of the interpolated functions and the original function, is shown in Fig. 13. Table 2 shows the average error per sample using fast filtering and Eq. 7. |
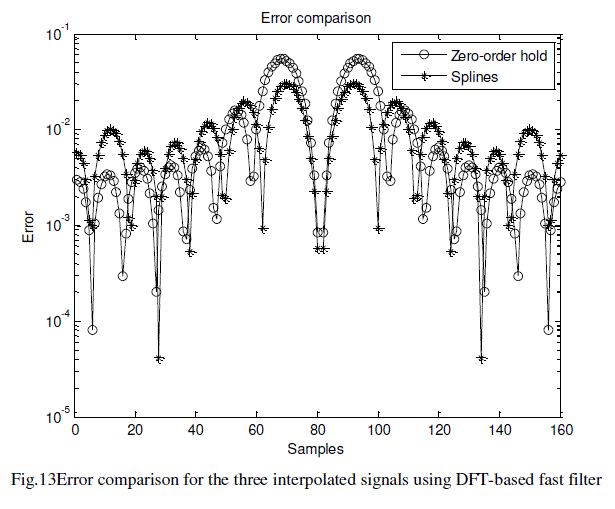 |
| With the fast filtering method, the signal with zero-order hold and the signal with spline insertion report a smaller error than when using convolution. Nevertheless, the interpolated signal with zero stuffing appears to overlap the original signal, presenting a despicable error. |
 |
| On average, the execution time for the fast filtering process using the DFT was 3.0353 ms. |
V. RESULTS |
| Considering the filters implemented by convolution with a length of 320 taps, there is a reported average error of 0.001, 0.013 and 0.009 respectively for the techniques of zero stuffing, zero-order hold and spline interpolation. These results show an error that can be slowly reduced for higher-order filters. Using the DFT-based fast filter, the obtained average error is: 0.000, 0.011 and 0.009 respectively for the techniques of zero stuffing, zero-order hold and spline interpolation. |
| The frequency domain analysis for the output of the convolution FIR filter shows that the interpolated signal using spline has the best response in the higher frequencies. This characteristic can be important if a suitable filtering stage is not possible. On the other hand, the signal with zero stuffing insertion does not alter the signal in the passband. In this case the reconstruction with the DFT-based fast filter showed a perfect reconstruction. Comparing the execution time, the fast filtering process using the DFT was 37 times faster than the convolution based filter. |
VI. CONCLUSION |
| The analysis of the different interpolation techniques shows that the spline-based interpolation and the zero-order hold techniques have a relatively small reconstruction error. This takes into account high-frequency ranges, which can be desirable if a suitable filtering stage is not available. However, these two insertion techniques add frequency components in the passband range. On the other hand, the technique of zero stuffing does not add new frequency components in the passband, but their images can cause a problem if the quality of the filter is not appropriate. |
| Both, the filter using convolution and the DFT-based fast filter, execute interpolation with a relatively small error. Nevertheless, the latter shows better results when the zero stuffing insertion technique is implemented because it suppresses the images that are the primary weakness of this technique. Therefore, the insertion technique of zero stuffing together with DFT-based fast filtering is a recommendable choice due to its low reconstruction error and lower computation time in comparison to the convolution filter. |
References |
|