Comparative Analysis of Vehicle Suspension
System in Matlab-SIMULINK and MSc-
ADAMS with the help of Quarter Car Model

S. J. Chikhale; Dr. S. P. Deshmukh

Comparative Analysis of Vehicle Suspension System in Matlab-SIMULINK and MSc- ADAMS with the help of Quarter Car Model

S. J. Chikhale¹, Dr. S. P. Deshmukh²

PG student, Dept. of Mechanical Engineering, SAE, Kondhawa, Pune, India
Professor, Dept. of Mechanical Engineering SAE, Kondhwa, Pune, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Scope of this paper is to prepare Quarter car model of vehicle suspension system in Matlab-SIMULINK and MSc-ADAMS. Mathematical model for quarter car is prepared with the help of State-Space representation. Then the quarter car model is developed in Matlab-SIMULINK and Msc-ADAMS. Vibration analysis is done by giving step input. Procedure and results are compared.

Keywords

Quarter car model, Vehicle suspension system, SIMULINK, MSc-ADAMS.

INTRODUCTION

Automotive industry is fastest growing industry in today’s era. The quality of the suspension system decides the future of the vehicle. One can say that suspension system works as WBC works in a blood. Analysing suspension system has become need of the automotive industry now days. Most of the research studies show that analysis of vehicle suspension systems is necessary to improve comfort of the passenger. To simplify the vibration analysis of the suspension system quarter car model is used. Quarter car model consist of the 1/4th of the total mass of the vehicle. According to the work done by O. GundogÃÂ du[1], the health of the driver is as important as the stability of the car, the desired objective is proposed as the minimization of a multi objective function formed by the combination of not only suspension deflection and tire deflection but also the head acceleration and crest factor (CF), which is not practiced as usual by the designers. Tamboli J. A. and Joshi S. G. [2], have found that the power spectral density of actual road profile follows an approximately exponentially decreasing curve. In “Quarter Model Analysis of Wagan-R car’s Rear Suspension using ADAMS”[3], they have prepared the quarter car model for rear suspension system in Pro-e. Then it is imported in the ADAMS for force and deflection analysis is done, saying that an excessive load will create discomfortness for sure as well as it affects on stability and ride handling. Most of the research studies includes the quarter car model for analysis. Li Xueying, Yu Zhuoping, and Xiong Lu,[4] says that, The torque vibration derived from inwheel- motor transmits to body frame through suspension system without the absorption of mechanical transmission parts, which influenced the quality of the vehicle NVH. In the present work, two quarter car models are prepared, One in the SIMULINK and other is in MSc-ADAMS. at first the mathematical model for quarter car is prepared using state space representation. This paper also discuss the development of quarter car model in SIMULINK first and then in MSc-ADAMS.

MATHEMATICAL MODEL

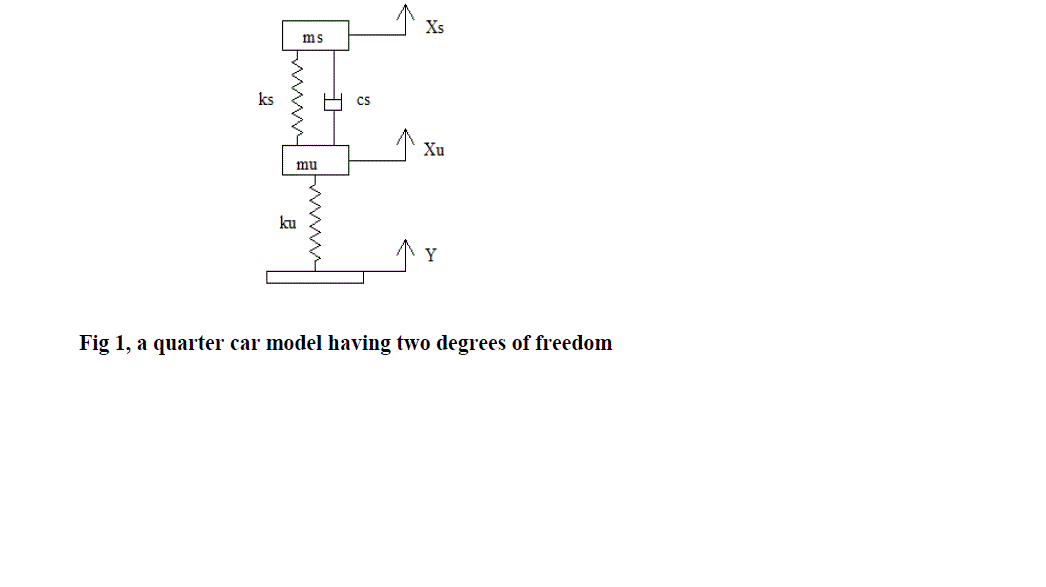
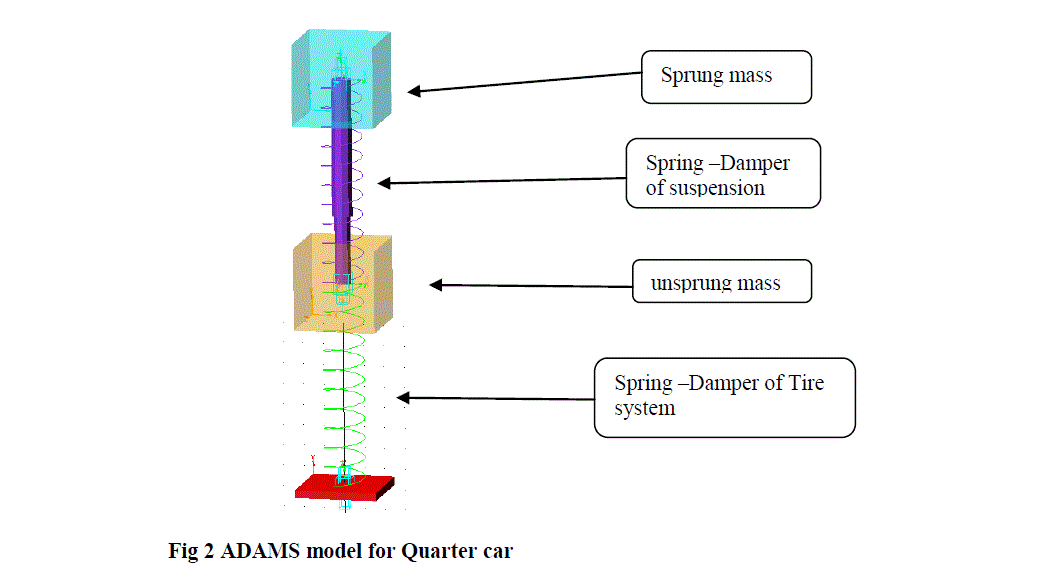
Tires and suspensions are considered in two degrees of freedom quarter car model as shown in Figure. This model is based on the bouncing motion of the vehicle due to random road surfaces. In this model only 1/4th of the vehicle is taken in to consideration for the vibration analysis. The model is two dimensional. Basically this model is consisting of one wheel which is specified by the spring in the diagram and sprung mass. Suspension system is shown by a simple spring damper system [5]. The advantage of this model is simplicity for the analysis. Fig. 1 shows the Quarter car model.

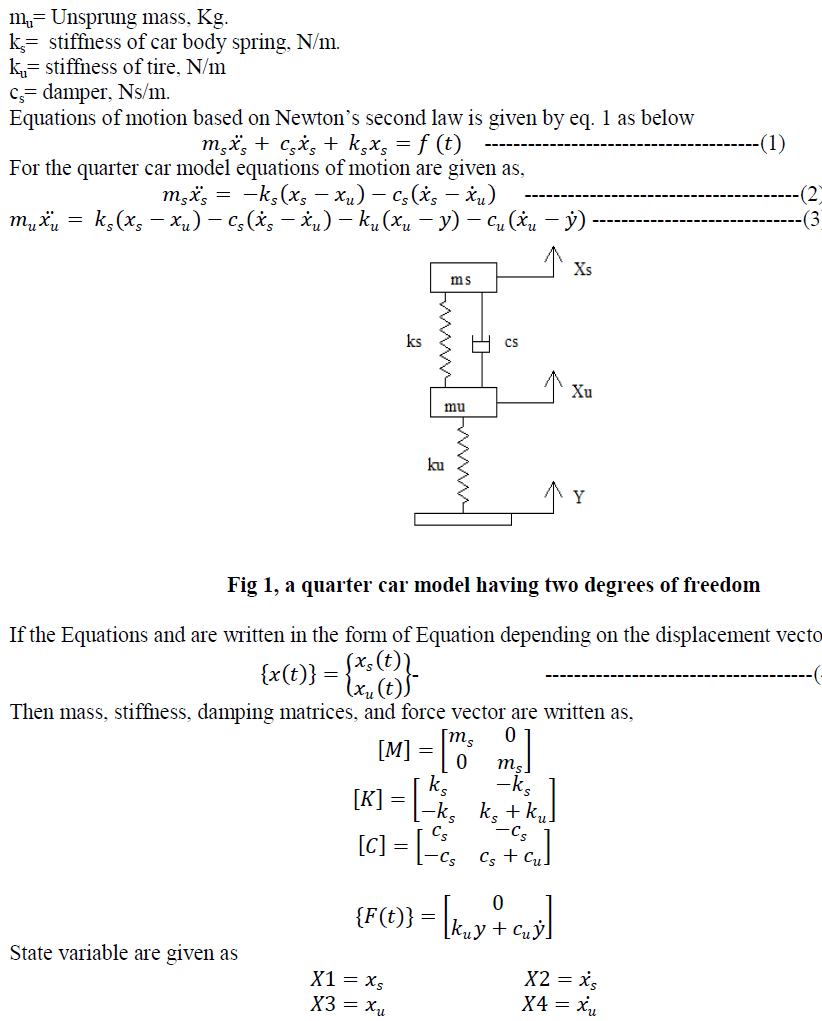Where,

X1 = displacement of sprung mass.

X2= velocity of sprung mass..

X3= displacement of unsprung mass.

X4= velocity of unsprung mass.

Substituting above values in equation 5 & 6, State space representation for quarter car model can be written as

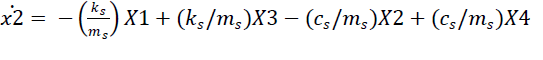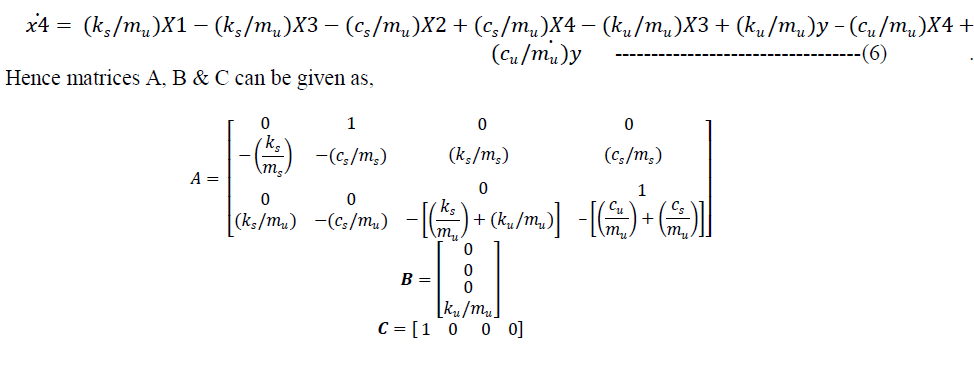MSC-ADAMS MODEL

For quarter car model 1/4th of the total sprung mass is considered. With reference of the diagram of the quarter car model from chapter 4, the procedure to build the model in ADAMS is given below.

VALIDATION OF MODEL

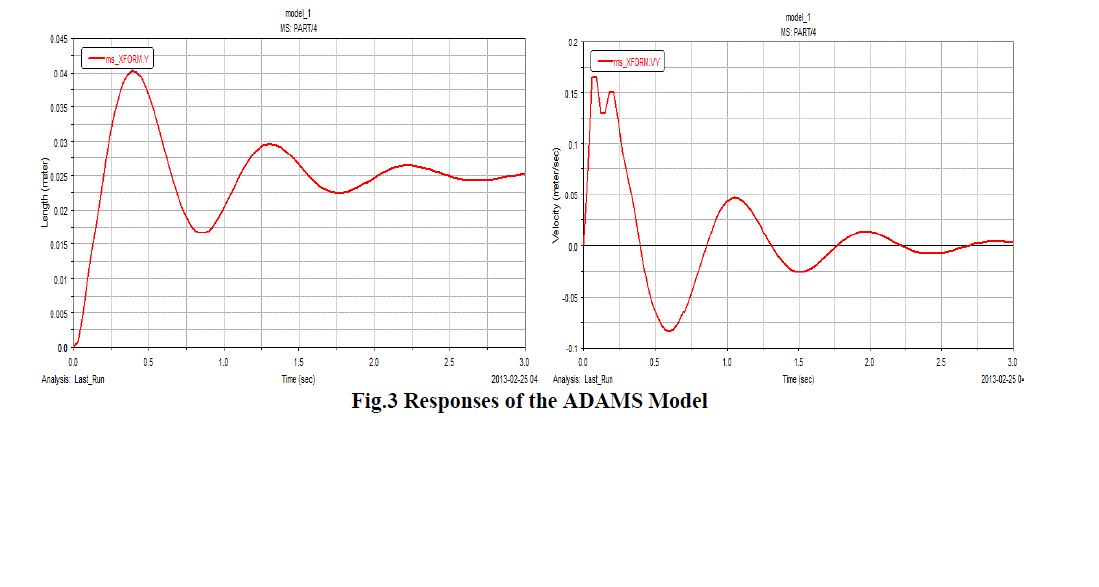
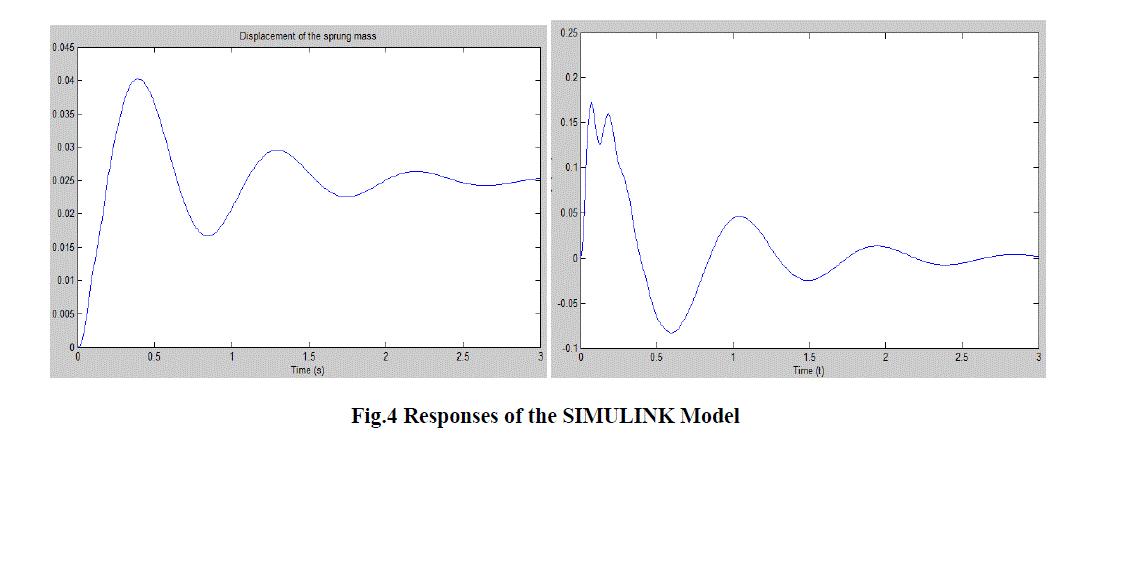
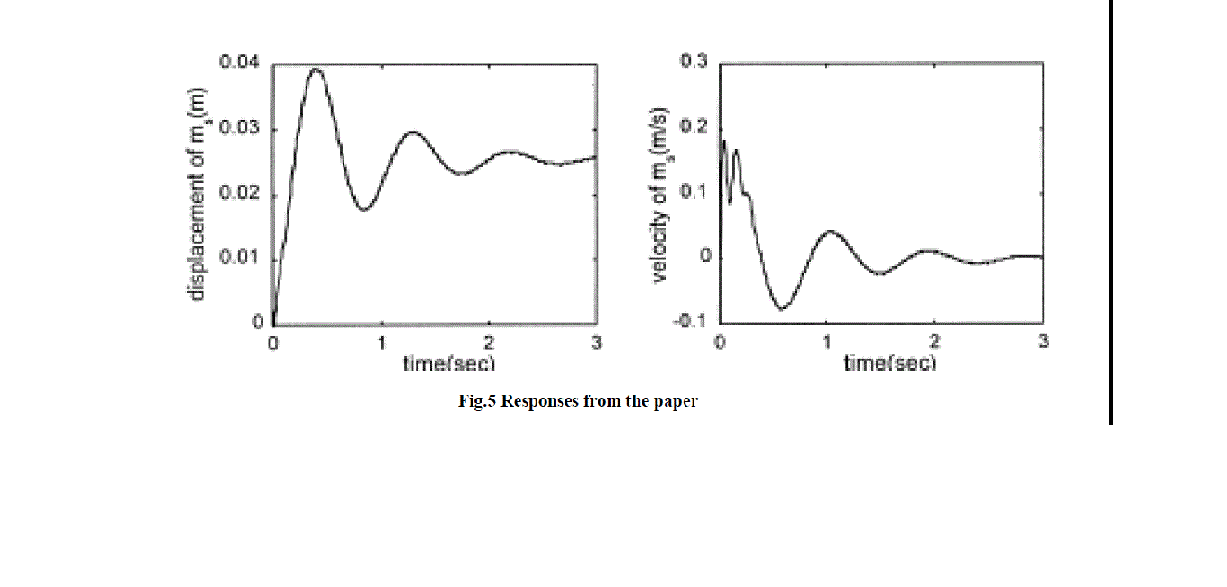
A quarter car models is prepared in the MATLAB-SIMULINK and ADAMS. To validate any model the input variables and the basic properties of the model element should be same. In this section , both the models ie SIMULINK and ADAMS are validated with each other and also validated with the paper “Reduced order modeling and parameter estimation for a quarter car model” published in Proc Instn Mech Engrs Vol. 214 part D [6] Given data:-

ms = 660.48; mu=132.82; cs=2167.8;

ks=36537; kt=331790;

For the above data and step input of the 0.025 m following are the results for the displacement of the sprung mass in SIMULINK, Adams and results from the paper.

RESULT AND DISCUSSION

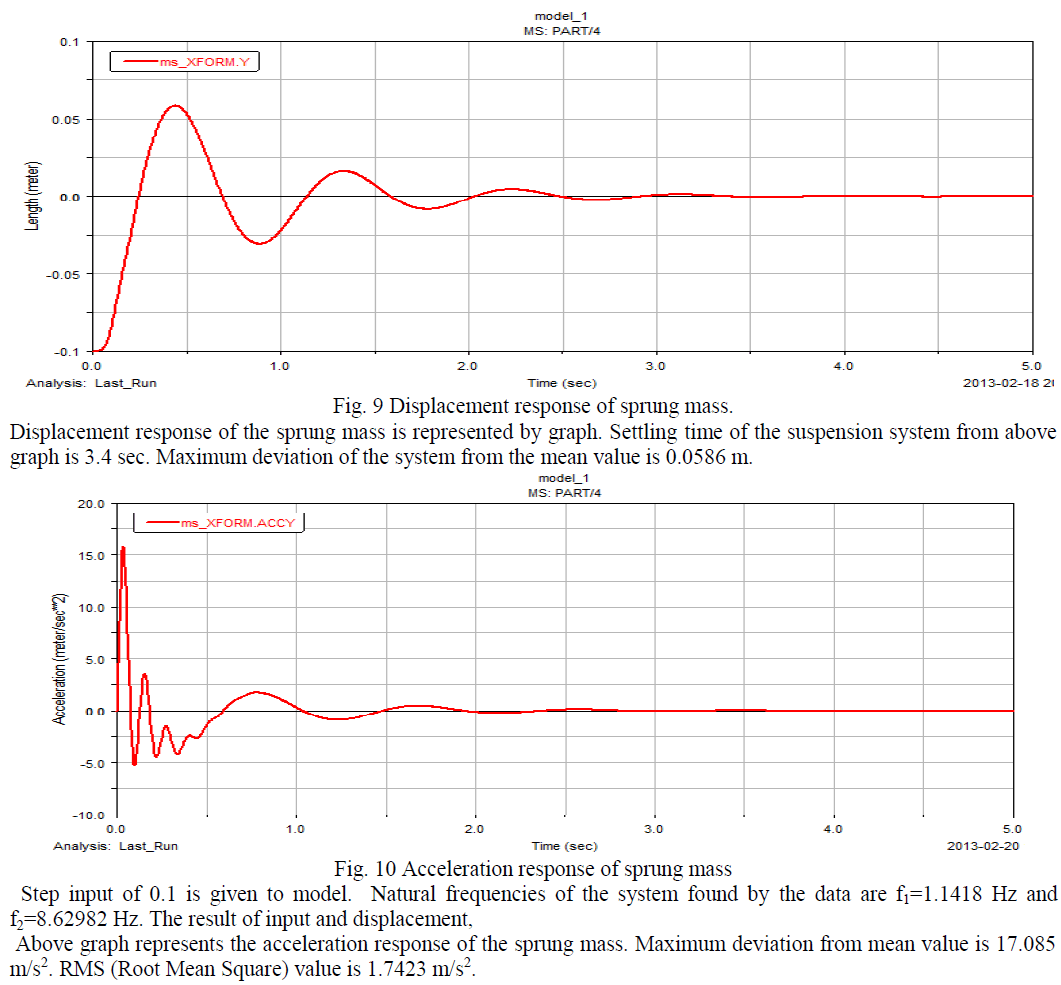
Vibration assessment depends strongly on the duration of exposure. The threshold limit value is not defined below 1 minute. Between 1 and 10 minutes a flat limit for aw is provided, which is inconsistent with the equal energy principle (implicit in the r.m.s. method). Because no precise statement is provided of what is meant by “period of exposure”, the result depends on the method used to subdivide the daily exposure, as well as on the arbitrary inclusion or exclusion of periods of low vibration. Finally, above 10 minutes the allowable acceleration is inversely proportional to the square root of duration. In spite of this law being restricted to durations in excess of 10 minutes, it still allows very large acceleration values because of the relative steepness of the relation between permissible acceleration and exposure time.Different response of the sprung mass, its settling time and maximum deviation from mean value for two different models is analyzed. For quarter car model, numerical values for the parameter of the vehicle are as follows, ms=290 Kg, mu=59 Kg, cs=1000 Ns/m, ks=16182 N/m, kt=190000 N/m,Step input of 0.1 is given to model. Natural frequencies of the system found by the data are w1=6.99 rad/sec and w2= 56.2 rad/sec. The result of input and displacement, velocity and Acceleration response of the sprung mass are given below,

CONCLUSION

Adams is the most widely used multibody dynamics and motion analysis software in the world. With the help of Adams, engineers can study the dynamics of moving parts, how loads and forces are distributed throughout mechanical systems, and to improve and optimize the performance of their products. We have seen how to prepare mathematical model and its representation in SIMULINK in the previous chapters. To create a simulink model we have to prepare the no. of equation of motion based on degree of freedom of the system. Then we use the blocks to represent those equations to find out result in simple manner. The most complicate part for simulation is to prepare the equation of motion for given model. In Msc-ADAMS we can directly represent these models without preparing any equation of motions which gives result in simpler manner.

References

O¨. Gundogdu Optimal seat and suspension design for a quarter car with driver model using genetic algorithms, International Journal of Industrial Ergonomics,vol. 37,2007-pp,327-332
Tamboli, J. A., and Joshi, S. G., “Optimum design of a passenger suspension system of a vehicle subjected to actual random road excitations”, Journal of Sound and Vibration, Vol. 219, 1999, pp. 193-205.
Patel “Quarter Model Analysis of Wagan-R cars Rear Suspension using ADAMS”
“ Simulation analysis and optimization design of front suspension based on ADAMS” , by Jihui Liang, Lili Xin
I. J. Nagrath, M. Gopal, “Systems modeling and analysis”, Tata McGraw-Hill publications.
C Kim, P I Ro. “Reduced order modeling and parameter estimation for a quarter car model” published in Proc Instn Mech Engrs Vol. 214 part D.