e-ISSN: 2319-9849
e-ISSN: 2319-9849
Department of Chemistry, Lomonosov Moscow State University, Russia
Received date: 18/09/2012; Revised date: 29/01/2013; Accepted date: 07/02/2013
Visit for more related articles at Research & Reviews: Journal of Chemistry
Five reaction schemes are suggested for the initiated nonbranched-chain addition of free radicals to the multiple bonds of the unsaturated compounds. The proposed schemes include reactions competing with chain propagation reactions through a reactive free radical. The chain evolution stage in these schemes involves three or four types of free radicals. One of them is relatively low-reactive and inhibits the chain process by shortening of the kinetic chain length. Based on the suggested schemes, nine rate equations (containing one to three parameters to be determined directly) are deduced using quasi-steady-state treatment. These equations provide good fits for the nonmonotonic (peaking) dependences of the formation rates of the molecular products (1:1 adducts) on the concentration of the unsaturated component in binary systems consisting of a saturated component (hydrocarbon, alcohol, etc.) and an unsaturated component (olefin, allyl alcohol, formaldehyde, or dioxygen). The unsaturated compound in these systems is both a reactant and an autoinhibitor generating low-reactive free radicals. A similar kinetic description is applicable to the nonbranched-chain process of the free-radical hydrogen oxidation, in which the oxygen with the increase of its concentration begins to act as an oxidation autoinhibitor (or an antioxidant). The energetics of the key radical-molecule reactions is considered.
binary system, unsaturated compound, low-reactive radical, autoinhibitor, competing reaction, nonbranched-chain addition, kinetic equation, rate, parameters, thermochemical data, energy, hydrogen.
In a binary system consisting of a saturated component and an unsaturated one, the abstraction of the most labile atom from a saturated molecule by some initiator converts this molecule into a saturated free radical (addend) capable of adding to the double bond of an unsaturated molecule to yield a saturated 1:1 adduct radical. At a sufficiently high concentration of the unsaturated component in the system, this primary adduct radical can add to another unsaturated molecule under certain conditions to yield a secondary, 1:2 adduct radical, and so on, resulting in telomerization. Under other conditions and at other relative reactivities of the components, the concentration of the saturated component can exceed the concentration of the unsaturated component so greatly that the most likely reaction for the primary adduct radical will be the abstraction of the least strongly bonded atom from a saturated molecule rather than addition. This reaction will yield a 1:1 adduct molecule as the ultimate product (it proceeds via a nonbranched-chain mechanism since it regenerates the saturated free radical carrying the chain). This reaction may compete with the parallel reaction between the 1:1 adduct radical and an unsaturated molecule. Even at a low concentration of the unsaturated component, this parallel reaction can proceed more efficiently owing to the formation, from the unsaturated molecule, of a free radical stabilized by the delocalization of the unpaired p-electron over, e.g., a system of conjugate bonds. This comparatively nonreactive radical does not participate in further chain propagation and inhibits the chain process, being consumed through reactions with the same radical and with the saturated addend radical. If the adduct radical abstracts some labile atom from an unsaturated molecule, it will again turn into the 1:1 adduct molecule, this time via a nonchain mechanism. The 1:1 adduct radical (which is the heaviest and the largest among the free radicals that result from the addition of one addend radical to the double bond of the molecule) may have an increased energy owing to the energy liberated in the transformation of a C=O, C=C, or O=O double bond into an ordinary bond (30–130 kJ mol–1 for the gas phase under standard conditions [1–4]). Therefore, it can decompose or react with one of the surrounding molecules in the place of its formation without diffusing in the solution and, hence, without participating in radical-radical chain termination reactions. Which of the two reactions of the adduct radical, the reaction with the saturated component or the reaction with the unsaturated component, dominates the kinetics of the process will depend on the reactivity and concentration ratios of the components in the binary system. In the processes of this kind, in which an addend radical and a lowreactivity, inhibiting radical are involved in three types of quadratic-law chain termination reactions, the formation rate of the 1:1 adduct as a function of the concentration of the unsaturated component has a maximum (which usually occurs at a low concentration of this component).
Earlier [5,6], there were attempts to describe such peaking dependences fragmentarily, assuming that the saturated or unsaturated component is in excess, in terms of the direct and inverse proportionalities, respectively, that result from the simplification of a particular case of the kinetic equation set up by the quasi-steady-state treatment of binary copolymerization involving fairly long chains [5]. This specific equation is based on an irrational function, whose plot is a monotonic curve representing the dependence of the product formation rate on the concentration of the unsaturated component. This curve comes out of the origin of coordinates, is convex upward, and has an asymptote parallel to the abscissa axis. Replacing the component concentrations with the corresponding mole fractions generates a peak in this irrational function and thereby makes it suitable to describe the experimental data [7]. However, this circumstance cannot serve as a sufficient validation criterion for the mechanism examined, because the new property imparted to the function by the above artificial transformation does not follow from the solution of the set of algebraic equations that are set up for the reaction scheme accepted for the process in a closed system and express the equality of the steady-state formation and disappearance rates of the reactive intermediates.
This publication presents a comprehensive review of the nonbranched-chain kinetic models developed for particular types of
additions of saturated free radicals to multiple bonds [8–14]. It covers free radical additions to olefins [10,11], their derivatives [8,9],
formaldehyde (first compound in the aldehyde homological series) [8,9,12], and oxygen [13,14] (which can add an unsaturated radical
as well) yielding various 1:1 molecular adducts, whose formation rates as a function of the unsaturated compound concentration pass
through a maximum (free radical chain additions to the С=N bond have not been studied adequately). In the kinetic description of
these nontelomerization chain processes, the reaction between the 1:1 adduct radical and the unsaturated molecule, which is in
competition with chain propagation through a reactive free radical (•PCl2, С2Н5 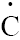 НОН, etc.), is included for the first time in the chain
propagation stage. This reaction yields a low-reactive radical (such as СН2=С(СН3)
НОН, etc.), is included for the first time in the chain
propagation stage. This reaction yields a low-reactive radical (such as СН2=С(СН3)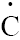 Н2 or Н
Н2 or Н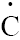 =О) and thus leads to chain
termination because this radical does not continue the chain and thereby inhibits the chain process [8]. We will consider kinetic
variants for the case of comparable component concentrations with an excess of the saturated component [10,11] and the case of an
overwhelming excess of the saturated component over the unsaturated component [8,9,12].
=О) and thus leads to chain
termination because this radical does not continue the chain and thereby inhibits the chain process [8]. We will consider kinetic
variants for the case of comparable component concentrations with an excess of the saturated component [10,11] and the case of an
overwhelming excess of the saturated component over the unsaturated component [8,9,12].
Based on the reaction schemes suggested for the kinetic description of the addition process, we have derived kinetic equations with
one to three parameters to be determined directly. Reducing the number of unknown parameters in a kinetic equation will allow one
to decrease the narrowness of the correlation of these parameters and to avoid a sharp buildup of the statistical error in the nonlinear
estimation of these parameters in the case of a limited number of experimental data points [15]. The rate constant of the addition of
a free radical to the double bond of the unsaturated molecule, estimated as a kinetic parameter, can be compared to its reference
value if the latter is known. This provides a clear criterion to validate the mathematical description against experimental data. The
kinetic equations were set up using the quasi-steady-state treatment. This method is the most suitable for processes that include
eight to ten or more reactions and four to six different free radicals and are described by curves based on no more than three to
seven experimental points. In order to reduce the exponent of the 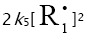 term in the
term in the 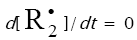 equation to unity [8], we used the following condition for the early stages of the process:
equation to unity [8], we used the following condition for the early stages of the process: 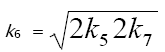 [16] and, hence, V1 = V5 + 2V6 + V7 =
[16] and, hence, V1 = V5 + 2V6 + V7 = 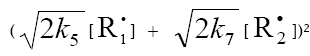 . Here,
. Here, 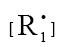 and
and 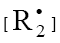 are the concentrations of the addend radical and the low-reactive
(inhibitor) radical, respectively; V1 is the initiation rate; V5, 2V6, and V7 are the rates of the three types of diffusion-controlled quadratic-law chain termination reactions; 2k5 and 2k7 are the rate constants of the loss of identical free radicals via the reactions
are the concentrations of the addend radical and the low-reactive
(inhibitor) radical, respectively; V1 is the initiation rate; V5, 2V6, and V7 are the rates of the three types of diffusion-controlled quadratic-law chain termination reactions; 2k5 and 2k7 are the rate constants of the loss of identical free radicals via the reactions 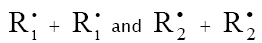 , respectively; k6 is the rate constant of the loss of different free radicals via the
, respectively; k6 is the rate constant of the loss of different free radicals via the 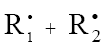 reaction
(see Schemes 1–5). The kinetic equations thus obtained fit the peaking rate curves well throughout the range of unsaturated component
concentrations in the binary systems. Our mathematical simulation was based on experimental data obtained for γ-radiation induced
addition reactions for which the initiation rate V1 is known.
reaction
(see Schemes 1–5). The kinetic equations thus obtained fit the peaking rate curves well throughout the range of unsaturated component
concentrations in the binary systems. Our mathematical simulation was based on experimental data obtained for γ-radiation induced
addition reactions for which the initiation rate V1 is known.
When reacting with olefins not inclined to free-radical polymerization, the free radicals originating from inefficient saturated telogens, such as alcohols [17] and amines [18], usually add to the least substituted carbon atom at the double bond, primarily yielding a free 1:1 adduct radical. This radical accumulates an energy of 90–130 kJ mol–1, which is released upon the transformation of the C=C bond to an ordinary bond (according to the data reported for the addition of nonbranched C1–C4 alkyl radicals to propene and of similar C1 and C2 radicals to 1-butene in the gas phase under standard conditions [1–4]). Such adduct radicals, which do not decompose readily for structural reasons, can abstract the most labile atom from a neighbor molecule of the saturated or unsaturated component of the binary reaction system, thus turning into a 1:1 adduct molecule. The consecutive and parallel reactions involved in this free-radical nonbranched-chain addition process are presented below (Scheme 1). In the case of comparable component concentrations with a nonoverwhelming excess of the saturated component, extra reaction (1b) (k1b 0) is included in the initiation stage [10,11]. In the case of an overwhelming excess of the saturated component reaction (1b) is ignored (k1b = 0) [8,9,12].
Comparable Component Concentrations
Scheme 1
Chain initiation
1. 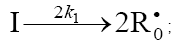
1a. 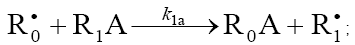
1b. 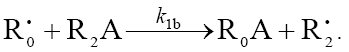
Chain propagation
2. 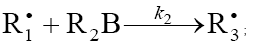
3. 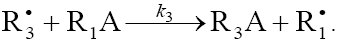
Inhibition
4. 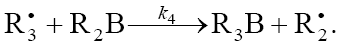
Chain termination
5. 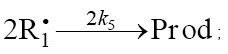
6. 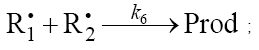
7. 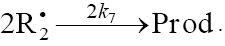
In this scheme, I is an initiator (e.g., a peroxide [5,12,13]); 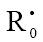 is a reactive (initiating) radical; A and B are hydrogen or halogen atoms [2,5,17–24]; R1 is •PCl2 [19], •CCl3 [20], alkyl [2,5], 1-hydroxyalkyl [5,6,17,22–24], or a similar functionalized reactive addend radical [5]; R2 is an alkenyl radical (allyl or higher) [2,5,17–22], 1-hydroxyalkenyl [5,17,18,23,24], or a similar functionalized lowreactive (inhibitor) radical [5,18];
is a reactive (initiating) radical; A and B are hydrogen or halogen atoms [2,5,17–24]; R1 is •PCl2 [19], •CCl3 [20], alkyl [2,5], 1-hydroxyalkyl [5,6,17,22–24], or a similar functionalized reactive addend radical [5]; R2 is an alkenyl radical (allyl or higher) [2,5,17–22], 1-hydroxyalkenyl [5,17,18,23,24], or a similar functionalized lowreactive (inhibitor) radical [5,18]; 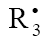 is a saturated reactive 1:1 adduct radical; R0A, R0B, and R1A are saturated molecules; R2B is an unsaturated molecule (olefin or its derivative); R3A and R3B are 1:1 adduct molecules; Prod designates the molecular products resulting from the dimerization or disproportionation of free radicals. The chain evolution (propagation and inhibition) stage of Scheme 1 include consecutive reactions 2 and 3, parallel (competing) reaction pairs 3 and 4, and consecutive-parallel reaction pair 2–4.
is a saturated reactive 1:1 adduct radical; R0A, R0B, and R1A are saturated molecules; R2B is an unsaturated molecule (olefin or its derivative); R3A and R3B are 1:1 adduct molecules; Prod designates the molecular products resulting from the dimerization or disproportionation of free radicals. The chain evolution (propagation and inhibition) stage of Scheme 1 include consecutive reactions 2 and 3, parallel (competing) reaction pairs 3 and 4, and consecutive-parallel reaction pair 2–4.
The initiation reaction 1 is either the decomposition of a chemical initiator [5,17,18] or a reaction induced by light [5,17,18] or
ionizing radiation [19–23]. The overall rate of chain initiation (reactions 1, 1a, and 1b) is determined by the rate of the rate-limiting
step (k1b > k1a). The reaction between the free radical 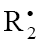 , which results from reactions 1b and 4, and the saturated molecule R1А is energetically unfavorable because it implies the formation of the free radical
, which results from reactions 1b and 4, and the saturated molecule R1А is energetically unfavorable because it implies the formation of the free radical 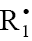 , which is less stable than the initial one. The addition reaction 2 may be accompanied by the abstraction reaction 2a.
, which is less stable than the initial one. The addition reaction 2 may be accompanied by the abstraction reaction 2a. 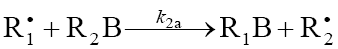 which yields the product R1B via a nonchain mechanism. Reaction 2a does not regenerate the addend radical
which yields the product R1B via a nonchain mechanism. Reaction 2a does not regenerate the addend radical 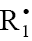 and is not
necessary for a kinetic description of the process, because the rate ratio of reactions 2 and 2a, V2/V2a = k2/k2a , is independent of the concentration of the unsaturated component R2B in the system. The inhibition of the nonbranched-chain addition process is due to reaction 4, in which the adduct radical
and is not
necessary for a kinetic description of the process, because the rate ratio of reactions 2 and 2a, V2/V2a = k2/k2a , is independent of the concentration of the unsaturated component R2B in the system. The inhibition of the nonbranched-chain addition process is due to reaction 4, in which the adduct radical 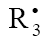 is spent in an inefficient way, since this reaction, unlike reaction 3, does not regenerate
is spent in an inefficient way, since this reaction, unlike reaction 3, does not regenerate 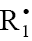 . The inhibiting effect is also due to the loss of chain carriers
. The inhibiting effect is also due to the loss of chain carriers 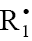 through their collisions with low-reactive unsaturated radicals
through their collisions with low-reactive unsaturated radicals 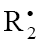 , but to a much lesser extent.
, but to a much lesser extent.
The rates of the formation (V, mol dm–3 s–1) of the 1:1 adducts R3A (via a chain mechanism) and R3B (via a nonchain mechanism) in reactions 3 and 4 are given by the equations
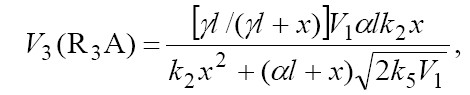 (1)
(1)
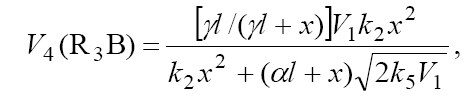 (2)
(2)
where V1 is the rate of the initiation reaction 1; l = [R1A] and x = [R2B] are the initial molar concentrations of the initial components, with l > x; k2 is the rate constant of the addition of the 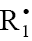 radical from the saturated component R1А to the unsaturated molecule R2В (reaction 2); and γ = k1a/k1b and α = k3/k4 are the rate constant ratios for competing (parallel) reactions (α is the first chain-transfer
constant for the free-radical telomerization process [5]). The rate ratio for the competing reactions is V3/V4 = αl/x, and the chain length is v = V3/V1.
radical from the saturated component R1А to the unsaturated molecule R2В (reaction 2); and γ = k1a/k1b and α = k3/k4 are the rate constant ratios for competing (parallel) reactions (α is the first chain-transfer
constant for the free-radical telomerization process [5]). The rate ratio for the competing reactions is V3/V4 = αl/x, and the chain length is v = V3/V1.
Earlier mathematical simulation [8] demonstrated that replacing the adduct radical R3 with the radical R2 [5] in the reaction between identical radicals and in the reaction involving R1 gives rise to a peak in the curve of the 1:1 adduct formation rate as a function of the concentration of the unsaturated component. Reaction 1b, which is in competition with reaction 1a, is responsible for the maximum in the curve described by Eq. (2), and reaction 4, which is in competition with reaction (3), is responsible for the maximum in the curve defined by Eq. (1).
The number of unknown kinetic parameters to be determined directly (k2, α, and γ) can be reduced by introducing the condition 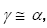 which is suggested by the chemical analogy between the competing reactions pairs 1a–1b and 3–4. For example, the ratios of the rate constants of the reactions of •OН, СН3О•, •СН3,
which is suggested by the chemical analogy between the competing reactions pairs 1a–1b and 3–4. For example, the ratios of the rate constants of the reactions of •OН, СН3О•, •СН3, 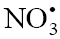 , and
, and 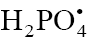 with methanol to the rate constants of the reactions of the same radicals with ethanol in aqueous solution at room temperature are 0.4–0.5 [25,26]. For the same purpose, the rate constant of reaction 2 in the kinetic equation can be replaced with its analytical expression
with methanol to the rate constants of the reactions of the same radicals with ethanol in aqueous solution at room temperature are 0.4–0.5 [25,26]. For the same purpose, the rate constant of reaction 2 in the kinetic equation can be replaced with its analytical expression 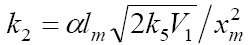 , which is obtained by
solving the quadratic equation following from the reaction rate extremum condition
, which is obtained by
solving the quadratic equation following from the reaction rate extremum condition 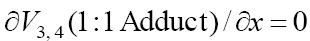 , where
, where 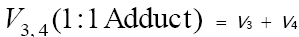 . After these transformations, the overall formation rate equation for the 1:1 adducts R3A and R3B (which may be identical, as in the case of R3H [5,8,9,12,13,18–21]), appears as
. After these transformations, the overall formation rate equation for the 1:1 adducts R3A and R3B (which may be identical, as in the case of R3H [5,8,9,12,13,18–21]), appears as
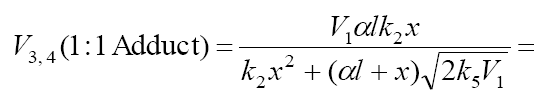 (3)
(3)
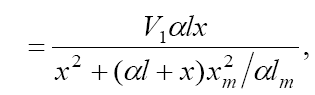 (3а)
(3а)
where lm and xm are the component concentrations l and x at the points of maximum of the function. Provided that V1 is known, the only parameter in Eq. (3a) to be determined directly is α. If V1 is known only for the saturated component R1A, then, for the binary system containing comparable R1A and R2B concentrations, it is better to use the quantity 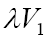 , where λ = l/(l + x) is the mole fraction of R1A, in place of V1 in Eqs. (3) and (3a).
, where λ = l/(l + x) is the mole fraction of R1A, in place of V1 in Eqs. (3) and (3a).
The two variable concentrations in the kinetic equation (3) – l and x – can be reduced to one variable by replacing them with the
corresponding mole fractions. Substituting the expression 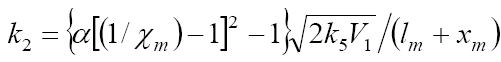 , derived from
the rate extremum condition, into this transformed equation for the binary system containing comparable component concentrations, we obtain
, derived from
the rate extremum condition, into this transformed equation for the binary system containing comparable component concentrations, we obtain
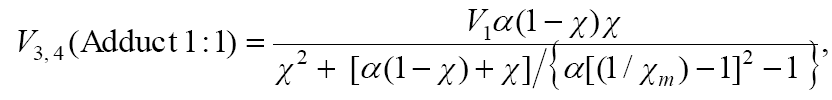 (3b)
(3b)
where 1 – χ = l/(l + x) and χ = x/(l + x) are the mole fractions of the components R1A and R2В (0 < χ <1), respectively, and χm is the χ value at the point of maximum.
The overall formation rate of the 1:1 adducts R3A and R3B is a sophisticated function of the formation and disappearance rates of the radicals 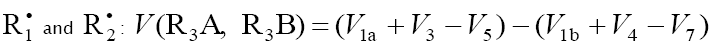 .
.
The application of the above rate equations to particular single nonbranched-chain additions is illustrated in Fig. 1. Curve 1 represents the results of simulation in terms of Eq. (3b) for the observed 1:1 adduct formation rate as a function of the initial mole fraction of the unsaturated component in the phosphorus trichloride–methylpropene1 reaction system at 303 K [19]. In this simulation, the 60Co γ-radiation dose rate was set at P = 0.01 Gy s–1 and the initiation yield was taken to be G(•PCl2) = 2.8 particles per 100 eV (1.60 × 10–17 J) of the energy absorbed by the solution [19]. The product of reaction 3 is Cl2PCH2C(Cl)(CH3)CH3 (two isomers), V1 = 4.65 × 10–9 mol dm–3 s–1 at χ = 0, and 2k5 = 3.2 × 108 dm3 mol–1 s–1. This leads to α = (2.5 ± 0.4) × 103, and the rate constant of reaction 2 derived from this α value is k2 = (1.1 ± 0.2) × 104 dm3 mol–1 s–1.
Figure 1: Reconstruction of the functional dependences (curves) of the product formation rates V3,4 (1) on the initial mole fraction of the unsaturated component (χ) from empirical data (symbols) using Eq. (3b) (model optimization with respect to the parameter α) for the phosphorus trichloride–methylpropene reaction system at 303 K [19] (standard deviation of SY = 2.58 × 10–6) and (2, ○) on the initial concentration of the unsaturated component (x) from empirical data (symbols) using Eq. (4a) (model optimization with respect to V1, хm, and α) for the 2-propanol–2-propen-1-ol system at 433 K [23] (SY = 5.91 × 10–7).
Note that, if the R2–B bond dissociation energy for the unsaturated component of the binary system is approximately equal to or
above, not below, the R1–A bond dissociation energy for the saturated component, than the rate of reaction 4 relative to the rate of
the parallel reaction 3 (chain propagation through the reactive free radical 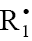 ) will be sufficiently high for adequate description of
R3A and R3B adduct formation in terms of Eqs. (1)–(3b) only at high temperatures [20]. In the phosphorus trichloride–propene system, the difference between the R2–B (B = H) and R1–A (A = Hal) bond dissociation energies in the gas phase under standard conditions [1] is as small as 5 kJ mol–1, while in the tetrachloromethane–methylpropene (or cyclohexene) and bromoethane–2-methyl-2-butene
systems, this difference is 20.9 (37.7) and ~24 kJ mol–1, respectively.
) will be sufficiently high for adequate description of
R3A and R3B adduct formation in terms of Eqs. (1)–(3b) only at high temperatures [20]. In the phosphorus trichloride–propene system, the difference between the R2–B (B = H) and R1–A (A = Hal) bond dissociation energies in the gas phase under standard conditions [1] is as small as 5 kJ mol–1, while in the tetrachloromethane–methylpropene (or cyclohexene) and bromoethane–2-methyl-2-butene
systems, this difference is 20.9 (37.7) and ~24 kJ mol–1, respectively.
Excess of the Saturated Component
If the concentration of the saturated component exceeds the concentration of the unsaturated component in the binary system, reaction 1b can be neglected. If this is the case (k1b = 0), then, in the numerators of the rate equations for reactions 3 and 4 (Eqs. (1) and (2)), γl/(γl + x) = 1 and the overall rate equation for the formation of the 1:1 adducts R3A and R3B will appear as
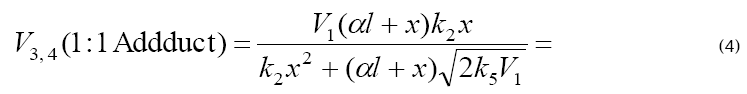 (4)
(4)
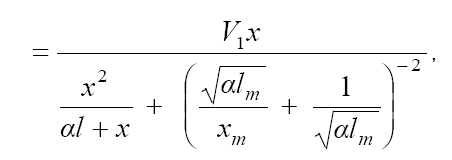 (4а)
(4а)
where the parameters are designated in the same way as in Eqs. (1)–(3a), l>> x, and k2 = 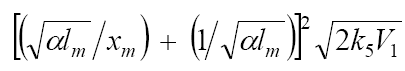 is determined from the condition
is determined from the condition 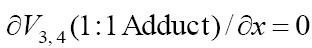 .
.
The rate equations for the chain termination reactions 5–7 (Scheme 1, k1b = 0) are identical to Eqs. (9)–(11) (see below) with β = 0.
Note that, if it is necessary to supplement Scheme 1 for k1b = 0 with the formation of R1B via the possible nonchain reaction 2a (which is considered in the Section 1.1), the parameter k2a should be included in the denominator of Eq. (4) to obtain 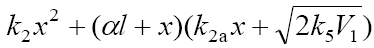 .
.
The analytical expression for k2 in the case of k2a ≠ 0 is identical to the expression for k2 for Eq. (4). The equation for the rate V2a(R1B) can be derived by replacing k2 with k2a in the numerator of Eq. (4) containing k2a in its denominator.
Curve 2 in Fig. 1 illustrates the good fit between Eq.(4a) and the observed 1:1 adduct formation rate as a function of the initial concentration of the unsaturated component in the reaction system 2-propanol–2-propen-1-ol at 433 K [8,9]. In this description, we used a 60Co γ-radiation dose rate of P = 4.47 Gy s–1 [23]. The product of reactions 3 and 4 is СН3(СН3)С(ОН)СН2СН2СН2ОН, and 2k5 = 1.0 × 1010 dm3 mol–1 s–1. The following parameters were obtained: V1 = (3.18 ± 0.4) × 106 mol dm–3 s–1, xm = (3.9 ± 0.5) × 10–2 mol dm–3, and α = (6.8 ± 0.8) × 10–2. The rate constant of reaction 2 derived from this α is k2 = (1.0 ± 0.14) × 105 dm3 mol–1 s–1.
Free radicals add to the carbon atom at the double bond of the carbonyl group of dissolved free (unsolvated, monomer) formaldehyde. The concentration of free formaldehyde in the solution at room temperature is a fraction of a percent of the total formaldehyde concentration, which includes formaldehyde chemically bound to the solvent [27]. The concentration of free formaldehyde exponentially increases with increasing temperature [28]. The energy released as a result of this addition, when the C=O bond is converted into an ordinary bond, is 30 to 60 kJ mol–1 (according to the data on the addition of С1–С4 alkyl radicals in the gas phase under standard conditions [1–4]). The resulting free 1:1 adduct radicals can both abstract hydrogen atoms from the nearest-neighbor molecules of the solvent or unsolvated formaldehyde and, due to its structure, decompose by a monomolecular mechanism including isomerization [9,12].
Addition of Free 1-Hydroxyalklyl Radicals with Two or More Carbon Atoms
Free 1-hydroxyalkyl radicals (which result from the abstraction of a hydrogen atom from the carbon atom bonded to the hydroxyl group in molecules of saturated aliphatic alcohols but methanol under the action of chemical initiators [29,30], light [17,31], or ionizing radiation [32,33]) add at the double bond of free formaldehyde dissolved in the alcohol, forming 1,2-alkanediols [8,9,12,29–36], carbonyl compounds, and methanol [8,33] via the chaining mechanism. (The yields of the latter two products in the temperature range of 303 to 448 K are one order of magnitude lower.) In these processes, the determining role in the reactivity of the alcohols can be played by the desolvation of formaldehyde in alcohol–formaldehyde solutions, which depends both on the temperature and on the polarity of the solvent [28,33]. For the γ-radiolysis of 1(or 2)-propanol–formaldehyde system at a constant temperature, the dependences of the radiation-chemical yields of 1,2-alkanediols and carbonyl compounds as a function of the formaldehyde concentration show maxima and are symbatic [8,32]. For a constant total formaldehyde concentration of 1 mol dm–3, the dependence of the 1,2-alkanediol yields as a function of temperature for 303–473 K shows a maximum, whereas the yields of carbonyl compounds and methanol increase monotonically [33] (along with the concentration of free formaldehyde [28]). In addition to the above products, the nonchain mechanism in the γ-radiolysis of the solutions of formaldehyde in ethanol and 1- and 2-propanol gives ethanediol, carbon monoxide, and hydrogen in low radiation-chemical yields (which, however, exceed the yields of the same products in the γ-radiolysis of individual alcohols) [8,9,33]. The available experimental data can be described in terms of the following scheme of reactions:
Scheme 2
Chain initiation
1. 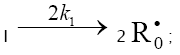
1a. 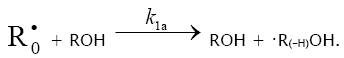
Chain propagation
2. 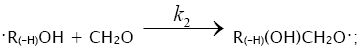
3. 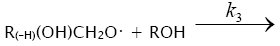
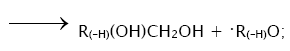
3a. 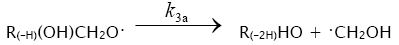
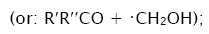
3b. 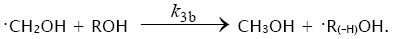
Inhibition
4. 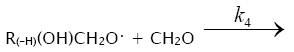
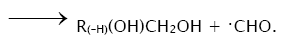
Chain termination
5. 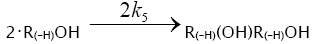
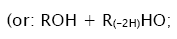
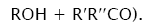
6. 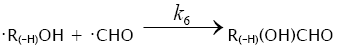
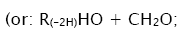
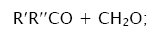
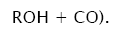
7. 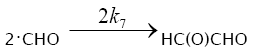
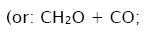
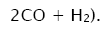
In these reactions, I is an initiator, e.g., a peroxide [29,30]; 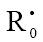 , some reactive radical (initiator radical); R, an alkyl; ROH, a saturated aliphatic alcohol, either primary or secondary, beginning from ethanol; CH2O, the unsaturated molecule – free formaldehyde; •СН2ОН, the 1-hydroxymetyl fragment radical; •R(–H)OH, the reactive 1-hydroxyalkyl radical (adduct radical), beginning from 1-hydroxyethyl; •СНО, the low-reactive formyl radical (inhibitor); R0H, the molecular product; R(–H)(OH)СН2ОН, 1,2-alkanediol; R(–2H)HO, an aldehyde in the case of a primary alcohol and an R'R"CO ketone in the case of a secondary alcohol; R(–H)(ОH)R(–H)ОH, a vicinal alkanediol; R(-H)(OH)CHO, a hydroxyaldehyde. The chain evolution stage of Scheme 2 includes consecutive reaction pairs 2–3, 2–3a, and 3a–3b; parallel (competing) reaction pairs 3–3a, 3–3b, 3–4, and 3a–4; and consecutive–parallel reactions 2 and 4.
, some reactive radical (initiator radical); R, an alkyl; ROH, a saturated aliphatic alcohol, either primary or secondary, beginning from ethanol; CH2O, the unsaturated molecule – free formaldehyde; •СН2ОН, the 1-hydroxymetyl fragment radical; •R(–H)OH, the reactive 1-hydroxyalkyl radical (adduct radical), beginning from 1-hydroxyethyl; •СНО, the low-reactive formyl radical (inhibitor); R0H, the molecular product; R(–H)(OH)СН2ОН, 1,2-alkanediol; R(–2H)HO, an aldehyde in the case of a primary alcohol and an R'R"CO ketone in the case of a secondary alcohol; R(–H)(ОH)R(–H)ОH, a vicinal alkanediol; R(-H)(OH)CHO, a hydroxyaldehyde. The chain evolution stage of Scheme 2 includes consecutive reaction pairs 2–3, 2–3a, and 3a–3b; parallel (competing) reaction pairs 3–3a, 3–3b, 3–4, and 3a–4; and consecutive–parallel reactions 2 and 4.
Scheme 2 does not include the same types of radical-molecule reactions as were considered in Section 1.1 for Scheme 1. In addition, it seems unlikely that free adduct radicals will add to formaldehyde at higher temperatures the reaction of adding is unlikely because this would result in an ether bond. The addition of hydroxymethyl radicals to formaldehyde, which is in competition with reaction 3b, is not included as well, because there is no chain formation of ethanediol at 303–448 K [33]. At the same time, small amounts of ethanediol can form via the dimerization of a small fraction of hydroxymethyl radicals, but this cannot have any appreciable effect on the overall process kinetics. The addition of free formyl radicals to formaldehyde cannot proceed at a significant rate, as is indicated by the fact that there is no chain formation of glycol aldehyde in the systems examined [33].
The mechanism of the decomposition of the free adduct radical via reaction 3a, which includes the formation of an intramolecular Н...О bond and isomerization, can be represented as follows [8,9,12]:
The probability of the occurrence of reaction 3a should increase with increasing temperature. This is indicated by experimental data
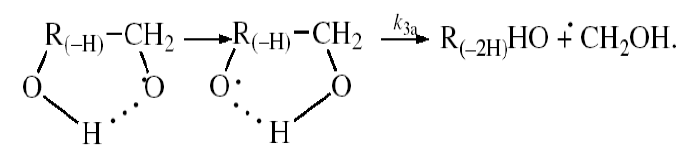
presented above [8,9,12]. The decomposition of the hydroxyalkoxyl radical. R(–H)(ОH)СН2О• (reaction 3a) is likely endothermic. The endothermic nature of reaction 3a is indirectly indicated by the fact that the decomposition of simple C2-C4 alkoxyl radicals RО• in the gas phase is accompanied by heat absorption: ( 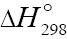 = 30-90 kJ mol–1 [2-4]). Reaction 3b, subsequent to reaction 3a, is exothermic, and its heat for C2-C3 alcohols in the gas phase is
= 30-90 kJ mol–1 [2-4]). Reaction 3b, subsequent to reaction 3a, is exothermic, and its heat for C2-C3 alcohols in the gas phase is 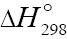 = -40 to -60 kJ mol–1 [2–4]. As follows from the above scheme of the process, reactions 3a and 3b, in which the formation and consumption of the highly reactive free radical hydroxymethyl take place (at equal rates under steady-state conditions), can be represented as a single bimolecular reaction 3a,b
occurring in a "cage" of solvent molecules.
= -40 to -60 kJ mol–1 [2–4]. As follows from the above scheme of the process, reactions 3a and 3b, in which the formation and consumption of the highly reactive free radical hydroxymethyl take place (at equal rates under steady-state conditions), can be represented as a single bimolecular reaction 3a,b
occurring in a "cage" of solvent molecules.
The free formyl radical resulting from reaction 4, which is in competition with reactions 3 and 3a, is comparatively low-reactive because its spin density can be partially delocalized from the carbon atom via the double bond toward the oxygen atom, which possesses a higher electron affinity [1]. For example, in contrast to the methyl and alkoxyl π-radicals, the formyl σ-radical can be stabilized in glassy alcohols at 77 K [37]. In the gas phase, the dissociation energy of the C–H bond in formyl radicals is half that for acetyl radicals and is about 5 times lower than the dissociation energy of the Cα–Н bond in saturated C1–C3 alcohols [1].
As distinct from reactions 3 and 3a,b, reaction 4 leads to an inefficient consumption of hydroxyalkoxyl adduct radicals, without
regenerating the initial 1-hydroxyalkyl addend radicals. Reaction 4 together with reaction 6 (mutual annihilation of free formyl and chain-carrier 1-hydroxyalkyl radicals) causes the inhibition of the nonbranched-chain process. For the disproportionation of the free
radicals, the heats of reactions 5-7 for C1-C3 alcohols in the gas phase vary in the range of 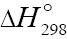 -Н = -135 to -385 kJ mol–1 [1-4].
-Н = -135 to -385 kJ mol–1 [1-4].
The rates of the chain formation of 1,2-alkanediols in reaction 3 (and their nonchain formation in reaction 4), carbonyl compounds in reaction 3a, and methanol in reaction 3b are given by the following equations:
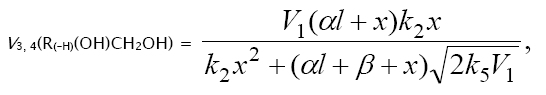 (5)
(5)
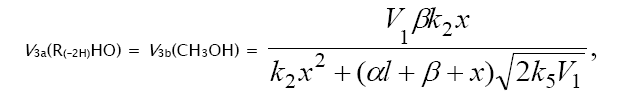 (6)
(6)
where V1 is the initiation rate, / is the molar concentration of the saturated alcohol at a given total concentration of formaldehyde2 dissolved in it, x is the initial molar concentration of free formaldehyde (l >> x), k2 is the rate constant of reaction 2 (addition of 1-hydroxyalkyl free radical to free formaldehyde), and α = k3/k4 and β = k3а/k4 (mol dm–3) are the ratios of the rate constants of the competing (parallel) reactions. Estimates of 2k5 were reported by Silaev et al. [39,40]. From the extremum condition for the reaction 3a rate function, 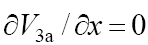 , we derived the following analytical expression:
, we derived the following analytical expression: 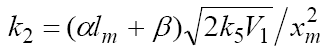 . The overall process rate is a complicated function of the formation and disappearance rates of the •R(–H)OH and •СНО free radicals:
V(R(–H)(OH)CH2OH, R(–2H)HO, CH3OH) = V1a + V3 + V3b – V4 – V5 + V7. The ratios of the rates of the competing reactions are V3/V4 = αl/x and V3a/V4 = β/x, and the chain length is v = (V3 + V3a)/V1. The ratio of the rates of formation of 1,2-alkanediol and the carbonyl compound is a simple linear function of x: V3,4(R(–H)(OH)CH2OH)/V3a(R(–2H)HO) = (k4/k3а)х + (k3/k3а)l. The equations for the rates of chain-termination reactions 5–7 are identical to Eqs. (9)–(11) (see below).
. The overall process rate is a complicated function of the formation and disappearance rates of the •R(–H)OH and •СНО free radicals:
V(R(–H)(OH)CH2OH, R(–2H)HO, CH3OH) = V1a + V3 + V3b – V4 – V5 + V7. The ratios of the rates of the competing reactions are V3/V4 = αl/x and V3a/V4 = β/x, and the chain length is v = (V3 + V3a)/V1. The ratio of the rates of formation of 1,2-alkanediol and the carbonyl compound is a simple linear function of x: V3,4(R(–H)(OH)CH2OH)/V3a(R(–2H)HO) = (k4/k3а)х + (k3/k3а)l. The equations for the rates of chain-termination reactions 5–7 are identical to Eqs. (9)–(11) (see below).
Figure 2 illustrates the use of Eqs. (5) and (6) for describing the experimental dependences of the formation rates of 1,2-butanediol (curve 1) in reactions 3 and 4 and propanal (curve 2) in reaction 3a on the initial concentration of free formaldehyde in the 1-
propanol–formaldehyde reacting system at a total formaldehyde concentration of 2.0 to 9.5 mol dm–3 and temperature of 413 K
[8,9,41]. The concentration dependence of the propanal formation rate was described using the estimates of kinetic parameters obtained for the same dependence of the 1,2-butanediol formation rate. We considered these data more reliable for the reason that the carbonyl compounds forming in the alcohol–formaldehyde systems can react with the alcohol and this reaction depends considerably on the temperature and acidity of the medium [27]. The mathematical modeling of the process was carried out using a 137Cs γ-radiation dose rate of P = 0.8 Gy s–1 [32,41], a total initiation yield of G(CH3СН2 НОН) = 9.0 particles per 100 eV [8,9] (V1 =
4.07 × 10–7 mol dm–3 s–1), and 2k5 = 4.7 × 109 dm3 mol–1 s–1). The following values of the parameters were obtained: α = 0.36 ± 0.07,β = 0.25 ± 0.05 mol dm–3, and k2 = (6.0 ± 1.4) × 103 dm3 mol–1 s–1.
НОН) = 9.0 particles per 100 eV [8,9] (V1 =
4.07 × 10–7 mol dm–3 s–1), and 2k5 = 4.7 × 109 dm3 mol–1 s–1). The following values of the parameters were obtained: α = 0.36 ± 0.07,β = 0.25 ± 0.05 mol dm–3, and k2 = (6.0 ± 1.4) × 103 dm3 mol–1 s–1.
Figure 2: Reconstruction of the functional dependence (curves) of the product formation rates V3,4 and V3а on the initial concentration x of free formaldehyde (model optimization with respect to the parameters α, β and k2) from empirical data (symbols) for the 1-propanol–formaldehyde system at 413 K [8,9,41]: (1) calculation using Eq. (5), standard deviation of SY = 2.20 × 10–7; (2) calculation using Eq. (6), SY = 2.38 × 10–8.
Note that, as compared to the yields of 1,2-propanediol in the γ-radiolysis of the ethanol–formaldehyde system, the yields of 2,3- butanediol in the γ-radiolysis of the ethanol–acetaldehyde system are one order of magnitude lower [41]. Using data from [8,9], it can be demonstrated that, at 433 K, the double bond of 2-propen-1-ol accepts the 1-hydroxyethyl radical 3.4 times more efficiently than the double bond of formaldehyde [42].
Addition of the Hydroxymethyl Radical
The addition of hydroxymethyl radicals to the carbon atom at the double bond of free formaldehyde molecules in methanol, initiated by the free-radical mechanism, results in the chain formation of ethanediol [34]. In this case, reaction 3a in Scheme 2 is the reverse of reaction 2, the 1-hydroxyalkyl radical •R(–H)OH is the hydroxymethyl radical •СН2ОН, so reaction 3b is eliminated(k3b = 0), and reaction 5 yields an additional amount of ethanediol via the dimerization of chain-carrier hydroxymethyl radicals (their disproportionation can practically be ignored [43]). The scheme of these reactions is presented in [35].
The rate equation for ethanediol formation by the chain mechanism in reaction 3 and by the nonchain mechanism in reactions 4 and 5 in the methanol–formaldehyde system has a complicated form3 as compared to Eq. (1) for the formation rate of the other 1,2- alkanediols [12]:
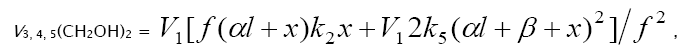 (7)
(7)
where 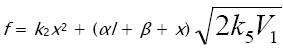 .
.
If the rate of ethanediol formation by the dimerization mechanism in reaction 5 is ignored for the reason that it is small as compared to the total rate of ethanediol formation in reactions 3 and 4, Eq. (7) will be identical to Eq. (5). After the numerator and denominator on the right-hand side of Eq. (5) are divided by k–2 ≡ k3a, one can replace k2 in this equation with K2 = k2/k–2, which is the equilibrium constant for the reverse of reaction 2. Ignoring the reverse of reaction 2 (k3a = 0, β = 0) makes Eq. (5) identical to Eq. (4) in Scheme 1 (see the Section 1). In this case, the rate constant k2 is effective.
The addition of a free radical or an atom to one of the two multiply bonded atoms of the oxygen molecule yields a peroxyl free radical and thus initiates oxidation, which is the basic process of chemical evolution. The peroxyl free radical then abstracts the most labile atom from a molecule of the compound being oxidized or decomposes to turn into a molecule of an oxidation product. The only reaction that can compete with these two reactions at the chain evolution stage is the addition of the peroxyl radical to the oxygen molecule (provided that the oxygen concentration is sufficiently high). This reaction yields a secondary, tetraoxyalkyl, 1:2 adduct radical, which is the heaviest and the largest among the reactants. It is less reactive than the primary, 1:1 peroxyl adduct radical and, as a consequence, does not participate in further chain propagation. At moderate temperatures, the reaction proceeds via a nonbranched-chain mechanism.
Addition of Hydrocarbon Free Radicals
Usually, the convex curve of the hydrocarbon (RH) autooxidation rate as a function of the partial pressure of oxygen ascends up to
some limit and then flattens out [6]. When this is the case, the oxidation kinetics is satisfactorily describable in terms of the
conventional reaction scheme [2,5,6,16,44,45], which involves two types of free radicals. These are the hydrocarbon radical R•
(addend radical) and the addition product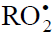 (1:1 adduct radical). However, the existing mechanisms are inapplicable to the cases in which the rate of initiated oxidation as a function of the oxygen concentration has a maximum (Figs. 3, 4) [46,47]. Such dependences can be described in terms of the competition kinetics of free-radical chain addition, whose reaction scheme involves not only the above two types of free radicals, but also an
(1:1 adduct radical). However, the existing mechanisms are inapplicable to the cases in which the rate of initiated oxidation as a function of the oxygen concentration has a maximum (Figs. 3, 4) [46,47]. Such dependences can be described in terms of the competition kinetics of free-radical chain addition, whose reaction scheme involves not only the above two types of free radicals, but also an 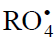 radical (1:2 adduct) inhibiting the chain process [13,14].
radical (1:2 adduct) inhibiting the chain process [13,14].
Figure 3: (1) Reconstruction of the functional dependence of the 2-methylbenzyl hydroperoxide formation rate V3(RO2H) on the initial dissolved oxygen concentration x from empirical data (points) using Eq. (3a) (model optimization with respect to the parameter α) for the o-xylene–oxygen system at 373 K [46] (standard deviation of SY = 5.37 × 10–7. (2) Reconstruction of the functional dependence of the total hydrogen peroxide formation rate V3, 7(Н2О2) on the initial dissolved oxygen concentration x from empirical data (symbols) using Eqs. (3a) and (12) with β = 0 (model optimization with respect to the parameter α) for the γ-radiolysis of water saturated with hydrogen and containing different amounts of oxygen at 296 K [63] (SY = 1.13 × 10–8). The dashed curve described V3(RO2H) as a function of the initial oxygen concentration x based on Eq. (3a) model optimization with respect to α) and the experimental data of curve 2 (SY = 1.73 × 10–8).
Figure 4: (1, 2) Quantum yields of (1, ●) hydrogen peroxide and (2, ○) water resulting from the photochemical oxidation of hydrogen in the hydrogen–oxygen system as a function of the initial oxygen concentration x (light wavelength of 171.9–172.5 nm, total pressure of 105 Pa, room temperature [64]). (3, 4) Hydrogen peroxide formation rate V(Н2О2) (dashed curves) as a function of the rate V(Н2О2) at which molecular oxygen is passed through a gas-discharge tube filled with (3) atomic and (4) molecular hydrogen. Atomic hydrogen was obtained from molecular hydrogen in the gas-discharge tube before the measurements (total pressure of 25–77 Pa, temperature of 77 K [47]). The symbols represent experimental data.
Scheme 3
Chain initiation
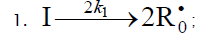
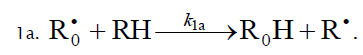
Chain propagation
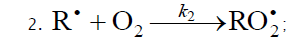
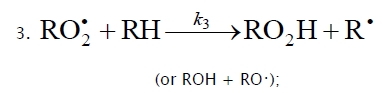
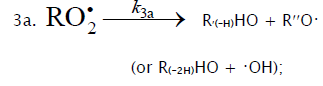
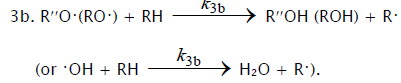
Inhibition
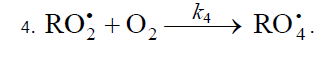
Chain termination:
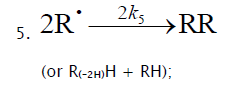
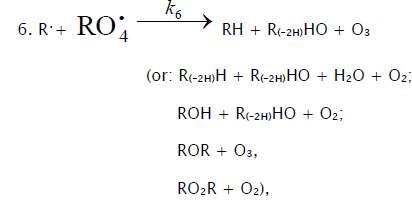
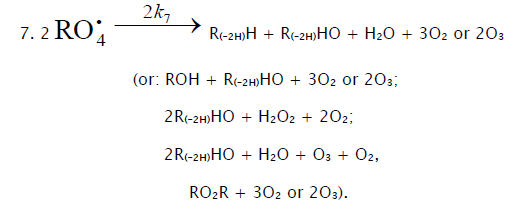
The only difference between the kinetic model of oxidation represented by Scheme 3 and the kinetic model of the chain addition of 1- hydroxyalkyl radicals to the free (unsolvated) form of formaldehyde in nonmethanolic alcohol–formaldehyde systems [8,9] (Scheme 2, Section 2.1) is that in the former does not include the formation of the molecular 1:1adduct via reaction 4.
The decomposition of the initiator I in reaction 1 yields a reactive  radical, which turns into the ultimate product R0H via reaction
1a, generating an alkyl radical R•, which participates in chain propagation. In reaction 2, the addition of the free radical R• to the
oxygen molecule yields a reactive alkylperoxyl 1:1 adduct radical
radical, which turns into the ultimate product R0H via reaction
1a, generating an alkyl radical R•, which participates in chain propagation. In reaction 2, the addition of the free radical R• to the
oxygen molecule yields a reactive alkylperoxyl 1:1 adduct radical 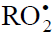 [45], which possesses increased energy owing to the energy
released upon the conversion of the O=O bond into the ordinary bond RО–О• (for addition in the gas phase under standard
conditions, this energy is 115–130 kJ mol–1 for C1–C4 alkyl radicals [1,2,4] and 73 kJ mol–1 for the allyl radical [4]). Because of this, the
adduct radical can decompose (reaction 3a) or react with some neighbor molecule (reaction 3 or 4) on the spot, without diffusing in
the solution and, accordingly, without entering into any chain termination reaction. In reaction 3, the interaction between the radical
adduct
[45], which possesses increased energy owing to the energy
released upon the conversion of the O=O bond into the ordinary bond RО–О• (for addition in the gas phase under standard
conditions, this energy is 115–130 kJ mol–1 for C1–C4 alkyl radicals [1,2,4] and 73 kJ mol–1 for the allyl radical [4]). Because of this, the
adduct radical can decompose (reaction 3a) or react with some neighbor molecule (reaction 3 or 4) on the spot, without diffusing in
the solution and, accordingly, without entering into any chain termination reaction. In reaction 3, the interaction between the radical
adduct 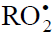 and the hydrocarbon molecule RH yields, via a chain mechanism, the alkyl hydroperoxide RO2H (this reaction
regenerates the chain carrier R• and, under certain conditions, can be viewed as being reversible [2]) or the alcohol ROH (this is
followed by the regeneration of R• via reaction 3b). The latter (alternative) pathway of reaction 3 consists of four steps, namely, the
breaking of old bonds and the formation of two new bonds in the reacting structures. In reaction 3a, the isomerization and
decomposition of the alkylperoxyl radical adduct
and the hydrocarbon molecule RH yields, via a chain mechanism, the alkyl hydroperoxide RO2H (this reaction
regenerates the chain carrier R• and, under certain conditions, can be viewed as being reversible [2]) or the alcohol ROH (this is
followed by the regeneration of R• via reaction 3b). The latter (alternative) pathway of reaction 3 consists of four steps, namely, the
breaking of old bonds and the formation of two new bonds in the reacting structures. In reaction 3a, the isomerization and
decomposition of the alkylperoxyl radical adduct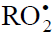 with O–O and C–O or C–H bond breaking take place [6,44], yielding the
carbonyl compound
with O–O and C–O or C–H bond breaking take place [6,44], yielding the
carbonyl compound 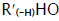 or R(–2Н)НО. Reaction 3b produces the alcohol R"OH or water and regenerates the free radical R• (here, R′
and R″ are radicals having a smaller number of carbon atoms than R). As follows from the above scheme of the process, consecutive
reactions 3a and 3b (whose rates are equal within the quasi-steady-state treatment), in which the highly reactive fragment, oxyl
radical R″О• (or •ОН) forms and then disappears, respectively, can be represented as a single, combined bimolecular reaction 3a,b
occurring in a "cage" of solvent molecules. Likewise, the alternative (parenthesized) pathways of reactions 3 and 3b, which involve the
alkoxyl radical RО•, can formally be treated as having equal rates. For simple alkyl C1–C4 radicals R, the pathway of reaction 3 leading
to the alkyl hydroperoxide RO2H is endothermic (
or R(–2Н)НО. Reaction 3b produces the alcohol R"OH or water and regenerates the free radical R• (here, R′
and R″ are radicals having a smaller number of carbon atoms than R). As follows from the above scheme of the process, consecutive
reactions 3a and 3b (whose rates are equal within the quasi-steady-state treatment), in which the highly reactive fragment, oxyl
radical R″О• (or •ОН) forms and then disappears, respectively, can be represented as a single, combined bimolecular reaction 3a,b
occurring in a "cage" of solvent molecules. Likewise, the alternative (parenthesized) pathways of reactions 3 and 3b, which involve the
alkoxyl radical RО•, can formally be treated as having equal rates. For simple alkyl C1–C4 radicals R, the pathway of reaction 3 leading
to the alkyl hydroperoxide RO2H is endothermic (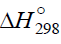 30–80 kJ mol–1) and the alternative pathway yielding the alcohol ROH is
exothermic (
30–80 kJ mol–1) and the alternative pathway yielding the alcohol ROH is
exothermic (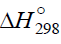 = –120 to –190 kJ mol–1), while the parallel reaction 3a, which yields a carbonyl compound and the alkoxyl
radical R″О• or the hydroxyl radical •ОН, is exothermic in both cases (
= –120 to –190 kJ mol–1), while the parallel reaction 3a, which yields a carbonyl compound and the alkoxyl
radical R″О• or the hydroxyl radical •ОН, is exothermic in both cases (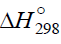 = –80 to –130 kJ mol–1), as also is reaction 3b
(
= –80 to –130 kJ mol–1), as also is reaction 3b
(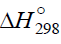 = –10 to –120 kJ mol–1), consecutive to reaction 3a, according to thermochemical data for the gas phase [2–4]. In reaction 4,
which is competing with (parallel to) reactions 3 and 3a (chain propagation through the reactive radical R•), the resulting low-reactive
radical that does not participate in further chain propagation and inhibits the chain process is supposed to be the alkyltetraoxyl 1:2
radical adduct4,5,
= –10 to –120 kJ mol–1), consecutive to reaction 3a, according to thermochemical data for the gas phase [2–4]. In reaction 4,
which is competing with (parallel to) reactions 3 and 3a (chain propagation through the reactive radical R•), the resulting low-reactive
radical that does not participate in further chain propagation and inhibits the chain process is supposed to be the alkyltetraoxyl 1:2
radical adduct4,5, 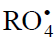 , which has the largest weight and size. This radical is possibly stabilized by a weak intramolecular H···Ohydrogen bond [54] shaping it into a six-membered cyclic structure6 (seven-membered cyclic structure in the case of aromatic and
certain branched acyclic hydrocarbons) [56,57]:
, which has the largest weight and size. This radical is possibly stabilized by a weak intramolecular H···Ohydrogen bond [54] shaping it into a six-membered cyclic structure6 (seven-membered cyclic structure in the case of aromatic and
certain branched acyclic hydrocarbons) [56,57]:
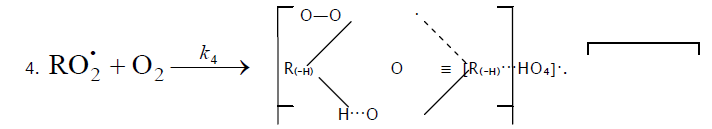
Reaction 4 in the case of the methylperoxyl radical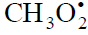 adding to the oxygen molecule to yield the methyltetraoxyl radical
adding to the oxygen molecule to yield the methyltetraoxyl radical 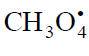 takes place in the gas phase, with heat absorption equal to 110.0 ± 18.6 kJ mol–1 [49] (without the energy of the possible
formation of a hydrogen bond taken into account). The exothermic reactions 6 and 7, in which the radical R• or
takes place in the gas phase, with heat absorption equal to 110.0 ± 18.6 kJ mol–1 [49] (without the energy of the possible
formation of a hydrogen bond taken into account). The exothermic reactions 6 and 7, in which the radical R• or 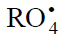 undergoes
disproportionation, include the isomerization and decomposition of the
undergoes
disproportionation, include the isomerization and decomposition of the 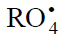 radical. The latter process is likely accompanied by
chemiluminescence typical of hydrocarbon oxidation [52]. These reactions regenerate oxygen as O2 molecules (including singlet
oxygen7 [52,59]) and, partially, as O3 molecules and yield the carbonyl compound R(–2H)HO (possibly in the triplet excited state [52]).
Depending on the decomposition pathway, the other possible products are the alcohol ROH, the olefin R(–2H)H (in the case of the
oxidation of a saturated hydrocarbon), the ether ROR, the alkyl peroxide RO2R, hydrogen peroxide, and water. It is likely that the
isomerization and decomposition of the
radical. The latter process is likely accompanied by
chemiluminescence typical of hydrocarbon oxidation [52]. These reactions regenerate oxygen as O2 molecules (including singlet
oxygen7 [52,59]) and, partially, as O3 molecules and yield the carbonyl compound R(–2H)HO (possibly in the triplet excited state [52]).
Depending on the decomposition pathway, the other possible products are the alcohol ROH, the olefin R(–2H)H (in the case of the
oxidation of a saturated hydrocarbon), the ether ROR, the alkyl peroxide RO2R, hydrogen peroxide, and water. It is likely that the
isomerization and decomposition of the 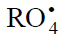 radical via reactions 6 and 7 can take place through the breaking of a C–C bond to
yield carbonyl compounds, alcohols, ethers, and organic peroxides containing fewer carbon atoms than the initial hydrocarbon, as in
the case of the alkylperoxyl radical
radical via reactions 6 and 7 can take place through the breaking of a C–C bond to
yield carbonyl compounds, alcohols, ethers, and organic peroxides containing fewer carbon atoms than the initial hydrocarbon, as in
the case of the alkylperoxyl radical 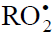 in reaction 3a. At later stages of oxidation and at sufficiently high temperatures, the
resulting aldehydes can be further oxidized into respective carboxylic acids. They can also react with molecular oxygen so that a C–H
bond in the aldehyde molecule breaks to yield two free radicals (
in reaction 3a. At later stages of oxidation and at sufficiently high temperatures, the
resulting aldehydes can be further oxidized into respective carboxylic acids. They can also react with molecular oxygen so that a C–H
bond in the aldehyde molecule breaks to yield two free radicals (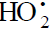 and
and 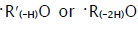 ). This process, like possible ozone
decomposition yielding an·•O• atom or peroxide decomposition with O–O bond breaking, leads to degenerate chain branching [6].
The equations describing the formation rates of molecular products at the chain propagation and termination stages of the above
reaction scheme, set up using the quasi-steady-state treatment, appear as follows:
). This process, like possible ozone
decomposition yielding an·•O• atom or peroxide decomposition with O–O bond breaking, leads to degenerate chain branching [6].
The equations describing the formation rates of molecular products at the chain propagation and termination stages of the above
reaction scheme, set up using the quasi-steady-state treatment, appear as follows:
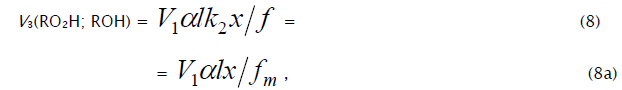
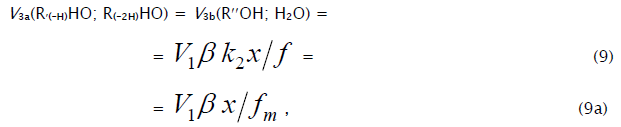
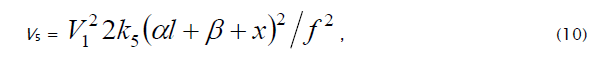
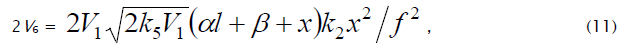

where V1 is the initiation rate, l = [RH] and x = [O2] are the initial molar concentrations of the starting components (l >> x), α = k3/k4 and β = k3a/k4 (mol dm–3) are the ratios of the rate constants of the competing (parallel) reactions, 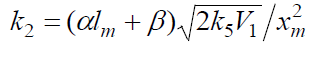 is the rate constant of the addition of the alkyl radical R• to the oxygen molecule (reaction 2)
as determined by solving the quadratic equation following from the rate function extremum condition
is the rate constant of the addition of the alkyl radical R• to the oxygen molecule (reaction 2)
as determined by solving the quadratic equation following from the rate function extremum condition 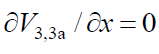 ,lm and xm are the values of l and x at the maximum point of the function, f = k2x2 + (αl + β + x)
,lm and xm are the values of l and x at the maximum point of the function, f = k2x2 + (αl + β + x) 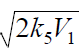 ,and
,and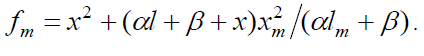
The ratios of the rates of the competing reactions are V3/V4 = αl/x and V3a/V4 = β/x, and the chain length is ν= (V3 + V3a)/V1. Eq. (9) is identical to Eq. (6). Eqs (8a) and (9a) were obtained by replacing the rate constant k2 in Eqs. (8) and (9) with its analytical expression (for reducing the number of unknown parameters to be determined directly).
For αl >> β (V3 >> V3a), when the total yield of alkyl hydroperoxides and alcohols having the same number of carbon atoms as the initial compound far exceeds the yield of carbonyl compounds, as in the case of the oxidation of some hydrocarbons, the parameter β in Eqs. (8) and 8a) can be neglected (β = 0) and these equations become identical to Eqs. (3) and (3a) with the corresponding analytical expression for k2.
In the alternative kinetic model of oxidation, whose chain termination stage involves, in place of R• (Scheme 3), 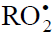 radicals
reacting with one another and with
radicals
reacting with one another and with 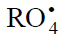 radicals, the dependences of the chain formation rates of the products on the oxygen
concentration x derived by the same method have no maximum:
radicals, the dependences of the chain formation rates of the products on the oxygen
concentration x derived by the same method have no maximum: 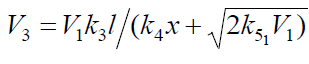 and
and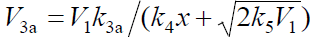 . In the kinetic model of oxidation that does not include the competing reaction 4 (k4 = 0) and
involves the radicals R• and
. In the kinetic model of oxidation that does not include the competing reaction 4 (k4 = 0) and
involves the radicals R• and  (the latter instead of
(the latter instead of  in Scheme 3) in reactions 5–7, the reaction rate functions V3 and V3a obtained in the same way are fractional rational functions in the form of a0x/(b0x + c0), where a0, b0, and c0 are coefficients having no
extremum. For a similar kinetic model in which reactions 3a,b and 4 appearing in the above scheme are missing (k3a = k4 = 0),
Walling [5], using the quasi-steady-state treatment in the long kinetic chain approximation, when it can be assumed that V2 = V3,
without using the substitution
in Scheme 3) in reactions 5–7, the reaction rate functions V3 and V3a obtained in the same way are fractional rational functions in the form of a0x/(b0x + c0), where a0, b0, and c0 are coefficients having no
extremum. For a similar kinetic model in which reactions 3a,b and 4 appearing in the above scheme are missing (k3a = k4 = 0),
Walling [5], using the quasi-steady-state treatment in the long kinetic chain approximation, when it can be assumed that V2 = V3,
without using the substitution 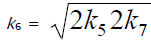 [5,6,16] (as distinct from this work), found that V2 = V3 is an irrational function of
[5,6,16] (as distinct from this work), found that V2 = V3 is an irrational function of 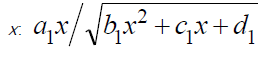 where a1, b1, c1, and d1 are coefficients. Again, this function has no maximum with respect to the
concentration of any of the two components.
where a1, b1, c1, and d1 are coefficients. Again, this function has no maximum with respect to the
concentration of any of the two components.
Thus, of the three kinetic models of oxidation mathematically analyzed above, which involve the radicals R• and in three types of quadratic-law chain termination reactions (reactions 5–7) and are variants of the conventional model [2,5,6,16,44,45], the last two lead to an oxidation rate versus oxygen concentration curve that emanates from the origin of coordinates, is convex upward, and has an asymptote parallel to the abscissa axis. Such monotonic dependences are observed when the oxygen solubility in the liquid is limited under given experimental conditions and the oxygen concentration attained8 is [O2]top ≤ xm.
Unlike the conventional model, the above kinetic model of free-radical nonbranched-chain oxidation, which includes the pairs of
competing reactions 3–4 and 3a–4 (Scheme 3), allows us to describe the nonmonotonic (peaking) dependence of the oxidation rate on
the oxygen concentration (Fig. 3). In this oxidation model, as the oxygen concentration in the binary system is increased, oxygen
begins to act as an oxidation autoinhibitor or an antioxidant via the further oxidation of the alkylperoxyl 1:1 adduct radical 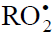 .
.
into the low-reactive 1:2 adduct radical 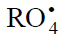 (reactions 4 and 6 lead to inefficient consumption of the free radicals
(reactions 4 and 6 lead to inefficient consumption of the free radicals 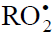 and R•
and cause shortening of the kinetic chains). The optimum oxygen concentration xm, at which the oxidation rate is the highest, can be
calculated using kinetic equations (8a) and (9a) and Eq. (3a) with β = 0 or the corresponding analytical expression for k2. In the
familiar monograph Chain Reactions by Semenov [60], it is noted that raising the oxygen concentration when it is already sufficient
usually slows down the oxidation process by shortening the chains. The existence of the upper (second) ignition limit in oxidation is
due to chain termination in the bulk through triple collisions between an active species of the chain reaction and two oxygen
molecules (at sufficiently high oxygen partial pressures). In the gas phase at atmospheric pressure, the number of triple collisions is
roughly estimated to be 103 times smaller than the number of binary collisions (and the probability of a reaction taking place depends
on the specificity of the action of the third particle).
and R•
and cause shortening of the kinetic chains). The optimum oxygen concentration xm, at which the oxidation rate is the highest, can be
calculated using kinetic equations (8a) and (9a) and Eq. (3a) with β = 0 or the corresponding analytical expression for k2. In the
familiar monograph Chain Reactions by Semenov [60], it is noted that raising the oxygen concentration when it is already sufficient
usually slows down the oxidation process by shortening the chains. The existence of the upper (second) ignition limit in oxidation is
due to chain termination in the bulk through triple collisions between an active species of the chain reaction and two oxygen
molecules (at sufficiently high oxygen partial pressures). In the gas phase at atmospheric pressure, the number of triple collisions is
roughly estimated to be 103 times smaller than the number of binary collisions (and the probability of a reaction taking place depends
on the specificity of the action of the third particle).
Curve 1 in Fig. 3 illustrates the fit between Eq. (3a) at αl >> β and experimental data for the radiation-induced oxidation of o-xylene in the liquid phase at 373 K in the case of 2-methylbenzyl hydroperoxide forming much more rapidly than o-tolualdehyde (V3 >> V3a and αl >> β) [46]. The oxygen concentration limit in o-xylene is reached at an oxygen concentration of [O2]top > xm, which corresponds to the third experimental point [46]. The oxygen concentration was calculated from the oxygen solubility in liquid xylene at 373 K [61]. The following quantities were used in this mathematical description: 60Co γ-radiation dose rate of P = 2.18 Gy s–1 and total initiation yield of G(o-СН3С6Н4ĊН2) = 2.6 particles per 100 eV of the energy absorbed by the solution [46]; V1 = 4.73 × 10–7 mol dm–3 s–1, and 2k5 = 1.15 × 1010 dm3 mol–1 s–1. The resulting value of the parameter α is (9.0 ± 1.8) × 10–3; hence, k2 = (3.2 ± 0.8) × 105 dm3 mol–1 s–1. From data presented in [62], is was estimated that k4 = k3/α = (5.2 ± 1.2) × 102 dm3 mol–1 s–1.
Addition of the Hydrogen Atom
A number of experimental findings concerning the autoinhibiting effect of an increasing oxygen concentration at modest temperatures on hydrogen oxidation both in the gas phase [47,64,65] (Fig. 4) and in the liquid phase [63] (Fig. 3, curve 2), considered in our earlier work [66], can also be explained in terms of the competition kinetics of free radical addition [14,67].
Scheme 4
Nonbranched-chain oxidation of hydrogen and changes in enthalpy ( 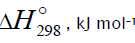 ) for elementary reactions9
) for elementary reactions9
Chain initiation

Chain propagation

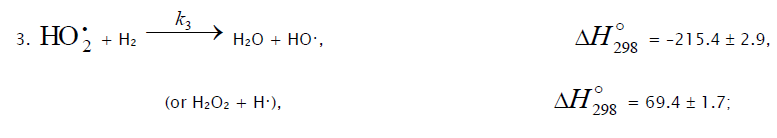

Inhibition

Chain termination




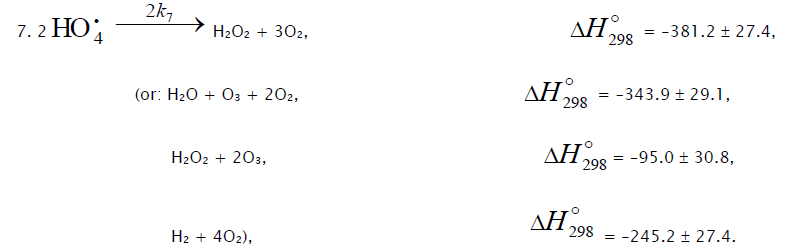
The hydroperoxyl free radical [75–79] resulting from reaction (2) possesses an increased energy due to the energy released
the conversion of the О=О double bond into an НО–О• ordinary bond. Therefore, before its possible decomposition, it can interact with a hydrogen or oxygen molecule as the third body via parallel (competing) reactions (3) and (4), respectively. The hydroxyl radical
НО• that appears and disappears in consecutive parallel reactions (3) (first variant) and 3′ possesses additional energy owing to the
exothermicity of the first variant of reaction 3, whose heat is distributed between the two products. As a consequence, this radical has
a sufficiently high reactivity not to accumulate in the system during these reactions, whose rates are equal (V3 = V3′) under quasisteady-
state conditions, according to the above scheme. Parallel reactions 3 (second, parenthesized variant) and 3′ regenerate
hydrogen atoms. It is assumed [56,57] that the hydrotetraoxyl radical
[75–79] resulting from reaction (2) possesses an increased energy due to the energy released
the conversion of the О=О double bond into an НО–О• ordinary bond. Therefore, before its possible decomposition, it can interact with a hydrogen or oxygen molecule as the third body via parallel (competing) reactions (3) and (4), respectively. The hydroxyl radical
НО• that appears and disappears in consecutive parallel reactions (3) (first variant) and 3′ possesses additional energy owing to the
exothermicity of the first variant of reaction 3, whose heat is distributed between the two products. As a consequence, this radical has
a sufficiently high reactivity not to accumulate in the system during these reactions, whose rates are equal (V3 = V3′) under quasisteady-
state conditions, according to the above scheme. Parallel reactions 3 (second, parenthesized variant) and 3′ regenerate
hydrogen atoms. It is assumed [56,57] that the hydrotetraoxyl radical 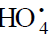 (first reported in [80]) resulting from endothermic reaction 4, which is responsible for the peak in the experimental rate curve (Fig. 2, curve 3), is closed into a five-membered [ОО─Н···ОО]• cycle due to
weak intramolecular hydrogen bonding [54,81]. This structure imparts additional stability to this radical and makes it least reactive.
(first reported in [80]) resulting from endothermic reaction 4, which is responsible for the peak in the experimental rate curve (Fig. 2, curve 3), is closed into a five-membered [ОО─Н···ОО]• cycle due to
weak intramolecular hydrogen bonding [54,81]. This structure imparts additional stability to this radical and makes it least reactive.
The 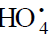 radical was discovered by Staehelin et al. [82] in a pulsed radiolysis study of ozone degradation in water; its UV spectrum
with an absorption maximum at 260 nm
radical was discovered by Staehelin et al. [82] in a pulsed radiolysis study of ozone degradation in water; its UV spectrum
with an absorption maximum at 260 nm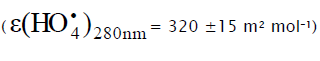 was reported. The spectrum of the
was reported. The spectrum of the 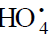 radical is
similar to that of ozone, but the molar absorption coefficient
radical is
similar to that of ozone, but the molar absorption coefficient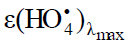 of the former is almost two times larger [82]. The
assumption about the cyclic structure of the
of the former is almost two times larger [82]. The
assumption about the cyclic structure of the 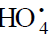 radical can stem from the fact that its mean lifetime in water at 294 K, which is
(3.6 ± 0.4) × 10–5 s (as estimated [66] from the value of 1/k for the reaction
radical can stem from the fact that its mean lifetime in water at 294 K, which is
(3.6 ± 0.4) × 10–5 s (as estimated [66] from the value of 1/k for the reaction 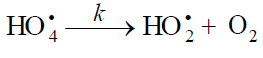 [82]), is 3.9 times
longer than that of the linear
[82]), is 3.9 times
longer than that of the linear 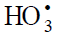 radical [68, 83] estimated in the same way [66] for the same conditions [84], (9.1 ± 0.9) × 10–6 s.
MP2/6-311++G** calculations using the Gaussian-98 program confirmed that the cyclic structure of
radical [68, 83] estimated in the same way [66] for the same conditions [84], (9.1 ± 0.9) × 10–6 s.
MP2/6-311++G** calculations using the Gaussian-98 program confirmed that the cyclic structure of 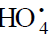 [85] is energetically
more favorable than the helical structure [68] (the difference in energy is 4.8–7.3 kJ mol–1, depending on the computational method
and the basis set).10 For example, with the MP2(full)/6-31G(d) method, the difference between the full energies of the cyclic and
acyclic
[85] is energetically
more favorable than the helical structure [68] (the difference in energy is 4.8–7.3 kJ mol–1, depending on the computational method
and the basis set).10 For example, with the MP2(full)/6-31G(d) method, the difference between the full energies of the cyclic and
acyclic 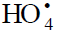 conformers with their zero-point energies (ZPE) values taken into account (which reduces the energy difference by 1.1
kJ mol–1) is –5.1 kJ mol–1 and the entropy of the acyclic-to-cyclic
conformers with their zero-point energies (ZPE) values taken into account (which reduces the energy difference by 1.1
kJ mol–1) is –5.1 kJ mol–1 and the entropy of the acyclic-to-cyclic 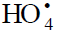 transition is
transition is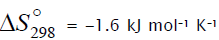 . Therefore, under
standard conditions,
. Therefore, under
standard conditions, 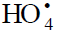 can exist in both forms, but the cyclic structure is obviously dominant (87%, Keq = 6.5) [85].
can exist in both forms, but the cyclic structure is obviously dominant (87%, Keq = 6.5) [85].
Reaction (4) and, to a much lesser degree, reaction (6) inhibit the chain process, because they lead to inefficient consumption of its
main participants 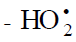 and Н•.acquire stability within the
and Н•.acquire stability within the
The hydrogen molecule that results from reaction (5) in the gas bulk possesses an excess energy, and, to
approximation used in this work, it should have time for deactivation via collision with a particle M capable of accepting the excess energy [87]. To simplify the form of the kinetic equations, it was assumed that the rate of the bimolecular deactivation of the molecule substantially exceeds the rate of its monomolecular decomposition, which is the reverse of reaction 5 [2].
Reactions (6) and (7) regenerate hydrogen and oxygen (in the form of 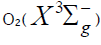 molecules, including the singlet states with
molecules, including the singlet states with 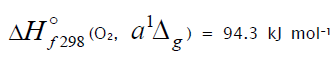 [49,70] and
[49,70] and 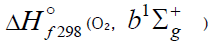 = 161.4 kJ mol–1 [70], which are deactivated by
collisions, and in the form of O3) and yield hydrogen peroxide or water via a nonchain mechanism, presumably through the
intermediate formation of the unstable hydrogen tetraoxide molecule H2O4 [88].11 Ozone does not interact with molecular hydrogen.
At moderate temperatures, it decomposes fairly slowly, particularly in the presence of О2
= 161.4 kJ mol–1 [70], which are deactivated by
collisions, and in the form of O3) and yield hydrogen peroxide or water via a nonchain mechanism, presumably through the
intermediate formation of the unstable hydrogen tetraoxide molecule H2O4 [88].11 Ozone does not interact with molecular hydrogen.
At moderate temperatures, it decomposes fairly slowly, particularly in the presence of О2 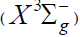 [70]. The reaction of ozone with Н• atoms, which is not impossible, results in their replacement with НО• radicals. The relative contributions from reactions 6 and 7 to the
process kinetics can be roughly estimated from the corresponding enthalpy increments (Scheme 4)
[70]. The reaction of ozone with Н• atoms, which is not impossible, results in their replacement with НО• radicals. The relative contributions from reactions 6 and 7 to the
process kinetics can be roughly estimated from the corresponding enthalpy increments (Scheme 4)
When there is no excess hydrogen in the hydrogen–oxygen system and the homomolecular dimer O4 [71–74,89,90], which exists at
low concentrations (depending on the pressure and temperature) in equilibrium with O2 [70], can directly capture the Н• atom to yield
the heteronuclear cluster 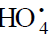 ,12 which is more stable than O4 [70] and cannot abstract a hydrogen atom from the hydrogen
molecule, nonchain hydrogen oxidation will occur to give molecular oxidation products via the disproportionation of free radicals.
The low-reactive hydrotetraoxyl radical
,12 which is more stable than O4 [70] and cannot abstract a hydrogen atom from the hydrogen
molecule, nonchain hydrogen oxidation will occur to give molecular oxidation products via the disproportionation of free radicals.
The low-reactive hydrotetraoxyl radical 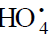 [82], which presumably has a high energy density [71], may be an intermediate in the
efficient absorption and conversion of biologically hazardous UV radiation energy the Earth upper atmosphere. The potential energy
surface for the atmospheric reaction HO• + О3, in which the adduct
[82], which presumably has a high energy density [71], may be an intermediate in the
efficient absorption and conversion of biologically hazardous UV radiation energy the Earth upper atmosphere. The potential energy
surface for the atmospheric reaction HO• + О3, in which the adduct 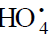 (2А) was considered as an intermediate, was calculated by
the DMBE method [91]. From this standpoint, the following reactions are possible in the upper troposphere, as well as in the lower
and middle stratosphere, where most of the ozone layer is situated (altitude of 16–30 km, temperature of 217–227 K, pressure of 1.0
× 104–1.2 × 103 Pa [92]; the corresponding
(2А) was considered as an intermediate, was calculated by
the DMBE method [91]. From this standpoint, the following reactions are possible in the upper troposphere, as well as in the lower
and middle stratosphere, where most of the ozone layer is situated (altitude of 16–30 km, temperature of 217–227 K, pressure of 1.0
× 104–1.2 × 103 Pa [92]; the corresponding  reaction values are given in kJ mol–1 [49]):
reaction values are given in kJ mol–1 [49]):
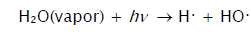 [92]; (8)
[92]; (8)


The 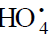 radical can disappear via disproportionation with a molecule, free radical, or atom in addition to dissociation. Note that
emission from О2
radical can disappear via disproportionation with a molecule, free radical, or atom in addition to dissociation. Note that
emission from О2 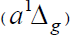 and
and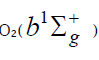 is observed at altitudes of 30–80 and 40–130 km, respectively [93].
is observed at altitudes of 30–80 and 40–130 km, respectively [93].
Staehelin et al. [82] pointed out that, in natural systems in which the concentrations of intermediates are often very low, kinetic chains in chain reactions can be very long in the absence of scavengers since the rates of the chain termination reactions decrease withdecreasing concentrations of the intermediates according to a quadratic law, whereas the rates of the chain propagation reactions decrease according to a linear law.
The kinetic description of the noncatalytic oxidation of hydrogen, including in an inert medium [87], in terms of the simplified scheme
of free-radical nonbranched-chain reactions (Scheme 4), which considers only quadratic-law chain termination and ignores the
surface effects [47], at moderate temperatures and pressures, in the absence of transitions to unsteady-state critical regimes, and at
a substantial excess of the hydrogen concentration over the oxygen concentration was obtained by means of quasi-steady-state
treatment, as in the previous studies on the kinetics of the branched-chain free-radical oxidation of hydrogen [76], even though the
applicability of this method in the latter case under unsteady states conditions was insufficiently substantiated. The method was used
with the following condition:13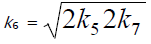 (see Introduction). The equation for the rate of the chain formation of hydrogen
peroxide and water, V3(H2O2; H2O) = V3′(H2O), via reactions 3 and 3′ is identical to Eq. (3, 3a) with the corresponding analytical
expression for k2. The ratio of the rates of the competing reactions is V3/V4 = αl/x, and the chain length is ν= V3/V1. The rates of
nonchain formation of hydrogen peroxide and water via reactions (6) and (7) – quadratic-law chain termination – are identical to Eqs.
(11) and (12) provided that β = 0. In these equations, l and x are the initial molar concentrations of hydrogen and oxygen (l >> x), lm
and xm are the respective concentrations at the maximum point of the function, V1 is the rate of initiation (reaction 1), α = k3/k4, the
rate constant
(see Introduction). The equation for the rate of the chain formation of hydrogen
peroxide and water, V3(H2O2; H2O) = V3′(H2O), via reactions 3 and 3′ is identical to Eq. (3, 3a) with the corresponding analytical
expression for k2. The ratio of the rates of the competing reactions is V3/V4 = αl/x, and the chain length is ν= V3/V1. The rates of
nonchain formation of hydrogen peroxide and water via reactions (6) and (7) – quadratic-law chain termination – are identical to Eqs.
(11) and (12) provided that β = 0. In these equations, l and x are the initial molar concentrations of hydrogen and oxygen (l >> x), lm
and xm are the respective concentrations at the maximum point of the function, V1 is the rate of initiation (reaction 1), α = k3/k4, the
rate constant 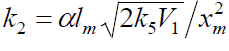 is derived from the condition ∂V3/∂x = 0, and 2k5 is the rate constan t of reaction 5
(hydrogen atom recombination), which is considered as bimolecular within the given approximation.14
is derived from the condition ∂V3/∂x = 0, and 2k5 is the rate constan t of reaction 5
(hydrogen atom recombination), which is considered as bimolecular within the given approximation.14
In the case of nonchain hydrogen oxidation via the above addition reaction 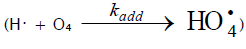 the formation rates of the
molecular oxidation products in reactions 6 and 7 (Scheme 4, k2 = k3 = k4 = 0) are defined by modified Eqs. (11) and (12) in which β
= 0, (αl + x) is replaced with 1, and k2 is replaced with kaddKeq (kaddKeq is the effective rate constant of Н• addition to the О4 dimer, Кeq k/k′ is the equilibrium constant of the reversible reaction
the formation rates of the
molecular oxidation products in reactions 6 and 7 (Scheme 4, k2 = k3 = k4 = 0) are defined by modified Eqs. (11) and (12) in which β
= 0, (αl + x) is replaced with 1, and k2 is replaced with kaddKeq (kaddKeq is the effective rate constant of Н• addition to the О4 dimer, Кeq k/k′ is the equilibrium constant of the reversible reaction 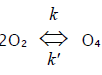 with
with  The formation rates of the stable
products of nonchain oxidation (k3 = 0), provided that either reactions (2) and (4) or reaction (2) alone (k4 = 0) occurs (Scheme 4; in
the latter case, reactions 6 and 7 involve the
The formation rates of the stable
products of nonchain oxidation (k3 = 0), provided that either reactions (2) and (4) or reaction (2) alone (k4 = 0) occurs (Scheme 4; in
the latter case, reactions 6 and 7 involve the  radical rather than
radical rather than  ), are given by modified Eqs. (11) and (12) with β = 0,
(αl + x) replaced with 1, and х2 replaced with х.Note that, if in Scheme 4 chain initiation via reaction 1 is due to the interaction between molecular hydrogen and molecular oxygen
yielding the hydroxyl radical НО• in stead of Н• atoms and if this radical reacts with an oxygen molecule (reaction 4) to form the
hydrotrioxyl radical
), are given by modified Eqs. (11) and (12) with β = 0,
(αl + x) replaced with 1, and х2 replaced with х.Note that, if in Scheme 4 chain initiation via reaction 1 is due to the interaction between molecular hydrogen and molecular oxygen
yielding the hydroxyl radical НО• in stead of Н• atoms and if this radical reacts with an oxygen molecule (reaction 4) to form the
hydrotrioxyl radical 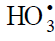 which was obtained in the gas phase by neutralization reionization (NR) mass spectrometry [83] and has a lifetime of >10–6 s at 298 K) and chain termination takes place via reactions 5–7 involving the НО• and
which was obtained in the gas phase by neutralization reionization (NR) mass spectrometry [83] and has a lifetime of >10–6 s at 298 K) and chain termination takes place via reactions 5–7 involving the НО• and 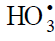 radicals instead ofН• and
radicals instead ofН• and 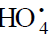 respectively, the expressions for the water chain formation rates derived in the same way will appear as a rational
function of the oxygen concentration x without a maximum:
respectively, the expressions for the water chain formation rates derived in the same way will appear as a rational
function of the oxygen concentration x without a maximum: 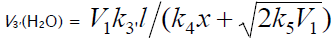 .
.
Curve 2 in Fig. 3 describes, in terms of the overall equation 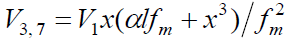 for the rates of reactions 3 and 7
(which was derived from Eqs. 3a and 12, respectively, the latter in the form of
for the rates of reactions 3 and 7
(which was derived from Eqs. 3a and 12, respectively, the latter in the form of 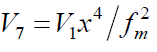 (12a) [96] in which k2 is replaced
with its analytical expression derived from Eq. (8) with β = 0 everywhere), the dependence of the hydrogen peroxide formation rate
(minus the rate
H2O2 V = 5.19 × 10–8 mol dm–3 s–1 of the primary formation of hydrogen peroxide after completion of the reactions in
spurs) on the initial concentration of dissolved oxygen during the γ-radiolysis of water saturated with hydrogen (7 × 10–4 mol dm–3) at
296 K [63]. These data were calculated in the present work from the initial slopes of hydrogen peroxide buildup versus dose curves
for a 60Co γ-radiation dose rate of Р = 0.67 Gy s–1 and absorbed doses of D ≅ 22.5–304.0 Gy. The following values of the primary
radiation-chemical yield G (species per 100 eV of energy absorbed) for water γ-radiolysis products in the bulk of solution at pH 4–9
and room temperature were used (taking into account that V = GP and V1 = GHP):
H2O2 G = 0.75 and GH = 0.6 (initiation yield; see
Conclusions) [94]; V1 = 4.15 × 10–8 mol dm–3 s–1; 2k5 = 2.0 × 1010 dm3 mol–1 s–1 [94]. As can be seen from Fig. 3, the best description
of the data with an increase in the oxygen concentration in water is attained when the rate V7 of the formation of hydrogen peroxide
via the nonchain mechanism in the chain termination reaction 7 (curve 1, α = (8.5 ± 2) × 10–2) is taken into account in addition to the
rate V3 of the chain formation of this product via the propagation reaction 3 (dashed curve 2, α = 0.11 ± 0.026). The rate constant of
addition reaction 2 determined from α is substantially underestimated: k2 = 1.34 × 107 (vs 2.0 × 1010 [94]) dm3 mol–1 s–1. The
difference can be due to the fact that the radiation-chemical specifics of the process were not considered in the kinetic description of
the experimental data. These include oxygen consumption via reactions that are not involved in the hydrogen oxidation scheme
[66,97,98] and reverse reactions resulting in the decomposition of hydrogen peroxide by intermediate products of water radiolysis
(
(12a) [96] in which k2 is replaced
with its analytical expression derived from Eq. (8) with β = 0 everywhere), the dependence of the hydrogen peroxide formation rate
(minus the rate
H2O2 V = 5.19 × 10–8 mol dm–3 s–1 of the primary formation of hydrogen peroxide after completion of the reactions in
spurs) on the initial concentration of dissolved oxygen during the γ-radiolysis of water saturated with hydrogen (7 × 10–4 mol dm–3) at
296 K [63]. These data were calculated in the present work from the initial slopes of hydrogen peroxide buildup versus dose curves
for a 60Co γ-radiation dose rate of Р = 0.67 Gy s–1 and absorbed doses of D ≅ 22.5–304.0 Gy. The following values of the primary
radiation-chemical yield G (species per 100 eV of energy absorbed) for water γ-radiolysis products in the bulk of solution at pH 4–9
and room temperature were used (taking into account that V = GP and V1 = GHP):
H2O2 G = 0.75 and GH = 0.6 (initiation yield; see
Conclusions) [94]; V1 = 4.15 × 10–8 mol dm–3 s–1; 2k5 = 2.0 × 1010 dm3 mol–1 s–1 [94]. As can be seen from Fig. 3, the best description
of the data with an increase in the oxygen concentration in water is attained when the rate V7 of the formation of hydrogen peroxide
via the nonchain mechanism in the chain termination reaction 7 (curve 1, α = (8.5 ± 2) × 10–2) is taken into account in addition to the
rate V3 of the chain formation of this product via the propagation reaction 3 (dashed curve 2, α = 0.11 ± 0.026). The rate constant of
addition reaction 2 determined from α is substantially underestimated: k2 = 1.34 × 107 (vs 2.0 × 1010 [94]) dm3 mol–1 s–1. The
difference can be due to the fact that the radiation-chemical specifics of the process were not considered in the kinetic description of
the experimental data. These include oxygen consumption via reactions that are not involved in the hydrogen oxidation scheme
[66,97,98] and reverse reactions resulting in the decomposition of hydrogen peroxide by intermediate products of water radiolysis
(  , Н•, НО•), with the major role played by the hydrated electron [94].
, Н•, НО•), with the major role played by the hydrated electron [94].
The general scheme of the nonbranched-chain addition of a free radical from a saturated compound to an olefin (and its functionalized derivative), formaldehyde, or dioxygen in liquid homogeneous binary systems of these components includes the following reactions [57,97,98].
Scheme 5
Initiation
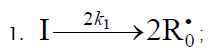
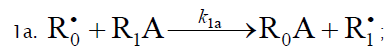
for addition to an olefin at comparable component concentrations,
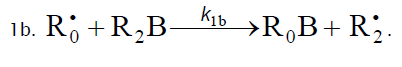
Chain propagation
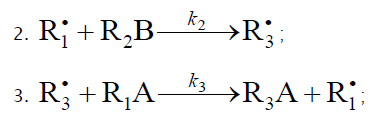
for addition to О2 and the 1-hydroxyalkyl radical to СН2О,
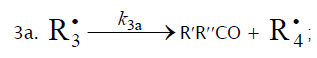
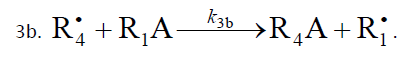
Inhibition
For addition to an olefin or СН2О,
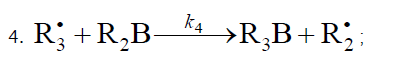
for addition to О2,
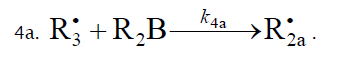
Chain termination
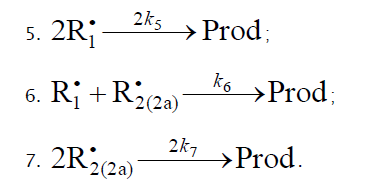
In this scheme, I is the initiator, for example, a peroxide [5,17,18,29,30]; 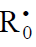 is any reactive radical (initiator); A is an atom of
hydrogen [2,5,6,17,18,22–24,29–32] or halogen [2,5,19–21]; B is an atom of hydrogen [5,17–21,23,24,29–32], halogen [22], or
oxygen (in oxidation) [2,5,6,16,44–46];
is any reactive radical (initiator); A is an atom of
hydrogen [2,5,6,17,18,22–24,29–32] or halogen [2,5,19–21]; B is an atom of hydrogen [5,17–21,23,24,29–32], halogen [22], or
oxygen (in oxidation) [2,5,6,16,44–46]; 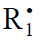 is a radical such as •PCl2 [19], •CCl3 [20], an alkyl [2,5,6,21], a 1-hydroxyalkyl
[5,6,17,22–24,29,32], or a similar functionalized radical [5] (addend);
is a radical such as •PCl2 [19], •CCl3 [20], an alkyl [2,5,6,21], a 1-hydroxyalkyl
[5,6,17,22–24,29,32], or a similar functionalized radical [5] (addend); 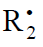 is the formyl [8,9,29], an alkenyl (propenyl or higher) [2,5,17–22], a 1-hydroxyalkenyl [5,17,18,23,24], or a similar functionalized low-reacrtive radical [5,18] (inhbitor) or the oxygen atom (in
oxidation) [2,5,6,13,14,16,44–46,56,57,96–98];
is the formyl [8,9,29], an alkenyl (propenyl or higher) [2,5,17–22], a 1-hydroxyalkenyl [5,17,18,23,24], or a similar functionalized low-reacrtive radical [5,18] (inhbitor) or the oxygen atom (in
oxidation) [2,5,6,13,14,16,44–46,56,57,96–98]; 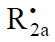 is the low-reactive alkyltetraoxyl 1:2 adduct radical
is the low-reactive alkyltetraoxyl 1:2 adduct radical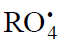 [13,14,56,57,96–98] (inhibitor);
[13,14,56,57,96–98] (inhibitor);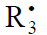 is the active 1:1 adduct radical;
is the active 1:1 adduct radical;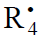 is an active fragment radical, such as hydroxymethyl [8,9,12,29,32], an
alkoxyl radical, or hydroxyl (in oxidation) [2,5,6,13,14,16,44,46,56,57,96–98]; R0A, R0B, R1A, and R4A are saturated molecules; R2B is an unsaturated molecule, viz., an olefin [2,5,11,17–22], formaldehyde [8,9,12,29–32], or dioxygen (in oxidation) [2,5,6,13,14,16,44–46,56,57,96–98]; R'R''CO is a carbonyl compound viz., aldehyde [2,6,8,9,12,14,29–32,44] or ketone [2,6,14,29,32,44]; R3A and R3B
are molecular products (1:1 adducts); and Prod stands for molecular products of the dimerization and disproportionation of free
radicals.
is an active fragment radical, such as hydroxymethyl [8,9,12,29,32], an
alkoxyl radical, or hydroxyl (in oxidation) [2,5,6,13,14,16,44,46,56,57,96–98]; R0A, R0B, R1A, and R4A are saturated molecules; R2B is an unsaturated molecule, viz., an olefin [2,5,11,17–22], formaldehyde [8,9,12,29–32], or dioxygen (in oxidation) [2,5,6,13,14,16,44–46,56,57,96–98]; R'R''CO is a carbonyl compound viz., aldehyde [2,6,8,9,12,14,29–32,44] or ketone [2,6,14,29,32,44]; R3A and R3B
are molecular products (1:1 adducts); and Prod stands for molecular products of the dimerization and disproportionation of free
radicals.
The chain evolution stage of Scheme 5 include consecutive reactions 2, 3; 2, 3a; and 3a, 3b; parallel (competitive) reactions 3, 3a; 3, 3b; 3, 4 (or 4a); and 3a, 4 (or 4a); and consecutive-parallel reactions 2 and 4 (or 4a). Addition to olefins is described by reactions 1–3, 4, and 5–7 and the corresponding rate equations (1)–(4a). Addition to the carbonyl carbon atom of the free (unsolvated) form of formaldehyde is represented by reactions 1, 1a, 2–4 (the main products are a 1,2-alkanediol, a carbonyl compound, and methanol), and 5–7 and is described by Eqs. (5) and (6). In the case of hydroxymethyl addition, the process includes reactions 1, 1a, 2, 3, 5a, 4 (the main product is ethanediol), and 5–7 and is described by Eq. (7). If the nonchain formation of ethanediol in reaction 5 is ignored, the process is described by Eq. (5). Addition to the oxygen molecule is described by reactions 1, 1a, 2–3b, 4a (the main products are an alkyl hydroperoxide, alcohols, carbonyl compounds, and water), and 5–7 and Eqs. (8), (8a), (9), and (9a).
The main molecular products of the chain process – 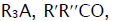 , and R4А – result from reactions 3, 3a, and 3b – chain propagation
through the reactive free radical
, and R4А – result from reactions 3, 3a, and 3b – chain propagation
through the reactive free radical 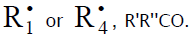 The competing reaction 4, which opposes this chain propagation, yields the
by-product R3B a nonchain mechanism. The rate of formation of the products is a complicated function of the formation rates (V3a = V3b) and disappearance rates of the free radicals
The competing reaction 4, which opposes this chain propagation, yields the
by-product R3B a nonchain mechanism. The rate of formation of the products is a complicated function of the formation rates (V3a = V3b) and disappearance rates of the free radicals 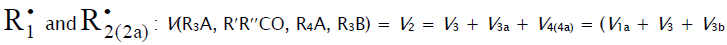
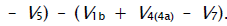 The rates of reactions 5–7 at k1b = 0 ([R1A] >> [R2B]) are given by Eqs. (9)–(11). The rate ratios of the
competing reactions are
The rates of reactions 5–7 at k1b = 0 ([R1A] >> [R2B]) are given by Eqs. (9)–(11). The rate ratios of the
competing reactions are 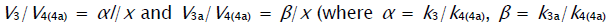 mol dm–3, and l and x are the initial
molar concentrations of the reactants R1A and R2B, respectively), and the chain length is
mol dm–3, and l and x are the initial
molar concentrations of the reactants R1A and R2B, respectively), and the chain length is 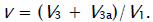 Unlike the dependences of
the rates of reactions 4a (or 4 at k1b = 0, with V4(4a) ≤ V1), 5, and 7 (Eqs. (9), (10), and (12)), the dependences of the rates V of reactions
3, 3a,b, 4 (at k1b ≠ 0), and 6 (Eqs. (1)–(9a) and (11)) on x have a maximum. Reaction 1b, which competes with reaction 1a, gives rise
to a maximum in the dependence described by Eq. (2), whereas reaction 4 or 4a, competing with reactions 3 and 3a,b, is responsible
for the maxima in the dependences defined by Eqs. (1), (3)–(7) or (8, 8a) and (9, 9a). The low-reactive radicals
Unlike the dependences of
the rates of reactions 4a (or 4 at k1b = 0, with V4(4a) ≤ V1), 5, and 7 (Eqs. (9), (10), and (12)), the dependences of the rates V of reactions
3, 3a,b, 4 (at k1b ≠ 0), and 6 (Eqs. (1)–(9a) and (11)) on x have a maximum. Reaction 1b, which competes with reaction 1a, gives rise
to a maximum in the dependence described by Eq. (2), whereas reaction 4 or 4a, competing with reactions 3 and 3a,b, is responsible
for the maxima in the dependences defined by Eqs. (1), (3)–(7) or (8, 8a) and (9, 9a). The low-reactive radicals 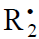 15 and
15 and 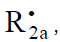 resulting from reactions 4 and 4a, inhibit the nonbranched-chain addition of
resulting from reactions 4 and 4a, inhibit the nonbranched-chain addition of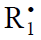 to olefins (or formaldehyde) and dioxygen,
respectively. Reaction 4a leads to non-productive loss of
to olefins (or formaldehyde) and dioxygen,
respectively. Reaction 4a leads to non-productive loss of 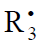 adduct radicals.
adduct radicals.
For approximate estimation of the parameters of the kinetic equations (3), (4), (8), and (9), Eq. (4) under the conditions 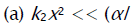
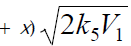 (ascending branch of a peaked curve) and (b)
(ascending branch of a peaked curve) and (b)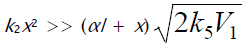 (descending branch) is transformed into
simple functions (direct and inverse proportionality, respectively) of the initial concentration x of the unsaturated compound. These
functions allow tentative estimates of the parameters k2 and α to be derived from the experimental product formation rate V provided
that V1 and 2k5 are known:
(descending branch) is transformed into
simple functions (direct and inverse proportionality, respectively) of the initial concentration x of the unsaturated compound. These
functions allow tentative estimates of the parameters k2 and α to be derived from the experimental product formation rate V provided
that V1 and 2k5 are known:
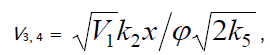 (13)
(13)
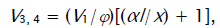 (14)
(14)
where φ = 1 under conditions (a) and (b) and φ = 2 at the point of maximum 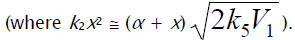 Equations (8) and (9)
under the condition
Equations (8) and (9)
under the condition 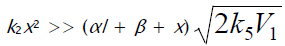 (descending branch of a peaked curve) can be transformed into Eqs. (15) and
(16), respectively, which express the simple, inversely proportional dependences of reaction rates on x and provide tentative
estimates of α and β:
(descending branch of a peaked curve) can be transformed into Eqs. (15) and
(16), respectively, which express the simple, inversely proportional dependences of reaction rates on x and provide tentative
estimates of α and β:
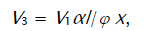 (15)
(15)
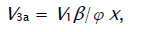 (16)
(16)
where φ = 2 at the point of maximum (where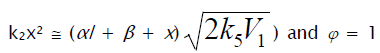 for the descending branch of the curve.
Equation (3) for V3, 4 under condition (b) transforms into Eq. (15).
for the descending branch of the curve.
Equation (3) for V3, 4 under condition (b) transforms into Eq. (15).
For radiation-chemical processes, the rates V in the kinetic equations should be replaced with radiation-chemical yields G using the
necessary unit conversion factors and the relationships 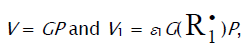 where P is the dose rate, ε1 is the electron fraction
of the saturated component R1A in the reaction system [100], and
where P is the dose rate, ε1 is the electron fraction
of the saturated component R1A in the reaction system [100], and 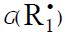 is the initial yield of the chain-carrier free radicals
(addends) – initiation yield [39,94].
is the initial yield of the chain-carrier free radicals
(addends) – initiation yield [39,94].
The optimum concentration of the unsaturated component in the system maximizing the process rate, xm, can be calculated using rate equations (3a), (4a), (8a), and (9a) or the corresponding analytical expressions for k2 provided that the other parameters involved in these equations are known. This opens up the way to intensification of some technological processes that are based on the addition of free radicals to С=С, С=О, and О=О bonds and occur via a nonbranched-chain mechanism through the formation of a 1:1 adduct.
The above data concerning the competition kinetics of the nonbranched-chain addition of saturated free radicals to the multiple bonds of olefins (and its derivatives), formaldehyde, and oxygen molecules make it possible to describe, using rate equations (1)–(9a), obtained by quasi-steady-state treatment, the peaking experimental dependences of the formation rates of molecular 1:1 adducts on the initial concentration of the unsaturated compound over the entire range of its variation in binary systems consisting of saturated and unsaturated components (Figs. 1–3). In such reaction systems, the unsaturated compound is both a reactant and an autoinhibitor, specifically, a source of low-reactive free radicals shortening kinetic chains. The progressive inhibition of the nonbranched-chain processes, which takes place as the concentration of the unsaturated compound is raised (after the maximum process rate is reached), can be an element of the self-regulation of the natural processes that returns them to the stable steady state.
A similar description is applicable to the nonbranched-chain free-radical hydrogen oxidation in water at 296 K [63] (Fig. 3, curve 2).
Using the hydrogen oxidation mechanism considered here, it has been demonstrated that, in the Earth’s upper atmosphere, the
decomposition of O3 in its reaction with the НО• radical can occur via the addition of the latter to the ozone molecule, yielding the 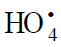 radical, which is capable of efficiently absorbing UV radiation [82].
radical, which is capable of efficiently absorbing UV radiation [82].
1In an earlier work [10], the methylpropene concentration in this system was overvalued by a factor of 1.7 when it was derived from the mole fractions given in [19].
2The alcohol concentration in alcohol–formaldehyde solutions at any temperature can be estimated by the method suggested in [38,39]. The data necessary for estimating the concentration of free formaldehyde using the total formaldehyde concentration in the solution are reported by Silaev et al. [28,39].
3In an earlier publication [8], this equation does not take into account reaction 3a.
4It is hypothesized that raising the oxygen concentration in the o-xylene–oxygen system can lead to the formation of an [RO•···O2] intermediate complex [46] similar to the [ROO•···(π-bond)RH] complex between the alkylperoxyl 1:1 adduct radical and an unsaturated hydrocarbon suggested in this work. The electronic structure of the π-complexes is considered elsewhere [48].
5Thermochemical data are available for some polyoxyl free radicals (the enthalpy of formation of the methyltetraoxyl radical without the energy of the possible intramolecular hydrogen bond Н···О taken into account is ΔНf˚298(C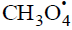 )= 121.3 ±15.3 kJ mol–1) and polyoxides (
)= 121.3 ±15.3 kJ mol–1) and polyoxides (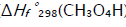 = –21.0 ±9 kJ mol–1) [49]. These data were obtained using the group contribution approach. Some
= –21.0 ±9 kJ mol–1) [49]. These data were obtained using the group contribution approach. Some
physicochemical and geometric parameters were calculated for the methyl hydrotetraoxide molecule as a model compound [50–52].
The IR spectra of dimethyl tetraoxide with isotopically labeled groups in Ar–O2 matrices were also reported [53]. For reliable determination of the number of oxygen atoms in an oxygen-containing species, it is necessary to use IR and EPR spectroscopy in
combination with the isotope tracer method [53].
6An 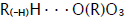 ring consisting of the same six atoms (C, H, and 4O), presumably with a hydrogen bond [6], also forms in the transition state of the dimerization of primary and secondary alkylperoxyl radicals RО2• via the Russell mechanism [5,55].
ring consisting of the same six atoms (C, H, and 4O), presumably with a hydrogen bond [6], also forms in the transition state of the dimerization of primary and secondary alkylperoxyl radicals RО2• via the Russell mechanism [5,55].
7Note that the alkylperoxyl radicals RО2• are effective quenchers of singlet oxygen О2(a1Δg)[58].
8The oxygen concentration attained in the liquid may be below the thermodynamically equilibrium oxygen concentration because of diffusion limitations hampering the establishment of the gas–liquid saturated solution equilibrium under given experimental conditions (for example, when the gas is bubbled through the liquid) or because the Henry law is violated for the given gas–liquid system under real conditions.
9According to Francisco and Williams [49], the enthalpy of formation (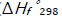 ) in the gas phase of
) in the gas phase of  (the latter
(the latter
without the possible intramolecular hydrogen bond taken into account), О3, Н2О [2], Н2О2, and Н2О4 is 218.0 ±0.0, 39.0 ±1.2, 12.6 ±1.7, 122.6 ±13.7, 143.1 ±1.7, –241.8 ±0.0, –136.0 ±0, and –26.0 ±9 kJ mol–1, respectively. Calculations for the radical with a helical structure were carried out using the G2(MP2) method [68]. The stabilization energies of
radical with a helical structure were carried out using the G2(MP2) method [68]. The stabilization energies of  were
were
calculated in the same work to be 64.5 ±0.1, 69.5 ±0.8, and 88.5 ±0.8 kJ mol–1, respectively. The types of the O4 molecular dimers, their IR spectra, and higher oxygen oligomers were reported [69,70]. The structure and IR spectrum of the hypothetical cyclotetraoxygen molecule O4, a species with a high energy density, were calculated by the CCSD method, and its enthalpy of formation was estimated [71]. The photochemical properties of O4 and the van der Waals nature of the О2–О2 bond were investigated [72,73]. The most stable geometry of the dimer is two O2 molecules parallel to one another. The O4 molecule was identified by NR mass spectrometry [74].
10There were calculations for the two conformers (cis and trans) of the  radical [86] using large scale ab initio methods and density functional techniques with extended basis sets. Both conformers have a nearly planar geometry with respect to the four oxygen atoms and present an unusually long central O–O bond. The most stable conformer of
radical [86] using large scale ab initio methods and density functional techniques with extended basis sets. Both conformers have a nearly planar geometry with respect to the four oxygen atoms and present an unusually long central O–O bond. The most stable conformer of  radical is the cis one, which is computed to be endothermic with respect to
radical is the cis one, which is computed to be endothermic with respect to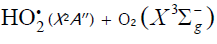 at 0 K.
at 0 K.
11The planar, six-atom, cyclic, hydrogen-bonded dimer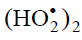 was calculated using quantum chemical methods (B3LYP density functional theory) [88]. The hydrogen bond energy is 47.7 and 49.4 kJ mol–1 at 298 K for the triplet and singlet states of the dimer, respectively.
was calculated using quantum chemical methods (B3LYP density functional theory) [88]. The hydrogen bond energy is 47.7 and 49.4 kJ mol–1 at 298 K for the triplet and singlet states of the dimer, respectively.
12It is impossible to make a sharp distinction between the two-step bimolecular interaction of three species via the equilibrium formation of the labile intermediate O4 and the elementary termolecular reaction 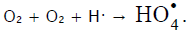
13For example, the ratio of the rate constants of the bimolecular disproportionation and dimerization of free radicals at room temperature is 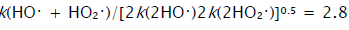 in the atmosphere [92] and
in the atmosphere [92] and 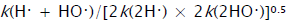 = 1.5 in water [94]. These values that are fairly close to unity.
= 1.5 in water [94]. These values that are fairly close to unity.
14This rate constant in the case of the pulsed radiolysis of ammonia–oxygen (+ argon) gaseous mixtures at a total pressure of 105 Pa and a temperature of 349 K was calculated to be 1.6 × 108 dm3 mol–1 s–1 [65] (a similar value of this constant for the gas phase was reported in an earlier publication [95]). Pagsberg et al. [65] found that the dependence of the yield of the intermediate НО• on the oxygen concentration has a maximum close to 5 × 10–4 mol dm–4 . In the computer simulation of the process, they considered the strongly exothermic reaction 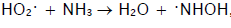 , which is similar to reaction 3 in Scheme 4, whereas the competing reaction 4 was not taken into account.
, which is similar to reaction 3 in Scheme 4, whereas the competing reaction 4 was not taken into account.
15The stabilization energy of the low-reactive free radicals СН2=С(СН3)ĊН2, СН2=СНĊНОН, and НĊ=O in the standard state in the gas phase is –52.0, –42.1, and –24.3 kJ mol–1, respectively [4,99].
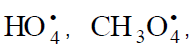 and
and : Ab Initio Quantum Chemical Calculations", Izvestiya Akademii Nauk, Ser.: Khimiya, No. 3, 2009, pp. 479–482, English Translation in: Russian Chemical Bulletin, International Edition, Vol. 58, No. 3, 2009, pp. 489–492.
: Ab Initio Quantum Chemical Calculations", Izvestiya Akademii Nauk, Ser.: Khimiya, No. 3, 2009, pp. 479–482, English Translation in: Russian Chemical Bulletin, International Edition, Vol. 58, No. 3, 2009, pp. 489–492.