ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Karthika.K1, Prithi Pavale2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This paper presents Trellis coded modulation with 8-PSK for Space communication. TCM is more suitable for space communication compared to other existing modulation techniques because of its bandwidth efficiency and better performance over fading channel. In TCM system higher coding gain can be achieved without expanding the bandwidth or increasing the average energy of the signal set. This includes concatenated system in which outer code is BCH and inner code TCM. The proposed concatenated system provides bandwidth efficiency compared to concatenated RS-TCM system. The simulated results show that significant coding gain by the proposed system over Additive White Gaussian Noise (AWGN) and Rayleigh fading channel.
Keywords |
| TCM, RS-TCM, BCH-TCM, AWGN. |
INTRODUCTION |
| Communication over space experiences signal fading. These systems have to operate over fading channels. Both AWGN and Rayleigh fading channels were considered in this paper. Bandwidth and power efficiency are becoming increasingly important as services have become more bandwidth demanding in addition to an increase system complexity. The Channel coding has been a traditional technique of combating signal fading. Most codes fall into either of two major categories: 1. Block codes 2. Convolutional codes 1) Block codes work with fixed length blocks of code. There are many types of block codes, but among the classical ones the most notable is Reed-Solomon coding because of its widespread use on the Compact disc, the DVD, and in hard disk drives. Other codes of classical block code include Golay, BCH,Multidimensional parity, and hamming codes. Classical block codes are usually implemented using hard-decision algorithms, which means that for every input and output signal a hard decision is made whether it corresponds to a one or a zero bit. 2) Convolutional codes deal with data sequentially (i.e. taken a few bits at a time) with the output depending on both the present input as well as previous inputs. The error correction power of a convolutional code increases with its constraint length. However, decoding complexity increases exponentially as the constraint length increases. Fortunately, the efficiency of the Viterbi algorithm allows the use of convolutional coding with quite reasonable constraint lengths in many applications. In contrast to block codes, soft-decision algorithms like the Viterbi decoder process (discretized) analog signals, which allows for much higher error-correction performance than hard-decision decoding. |
II. CONCATENATED CODES |
| In coding theory, combination of an inner code and an outer code forms aclass of error correcting codes known as concatenated codes. They are conceived in 1966 by Dave Forney. These codes have two advantages, that is decreasing error probability with increasing block length and polynomial time decoding complexity. Concatenated codes became widely used in space communications in the 1970s. |
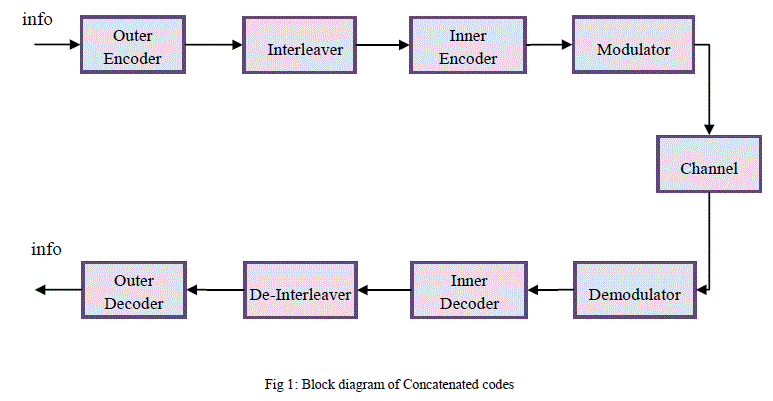 |
| Natural concepts for a decoding algorithm for concatenated codes is to first decode the inner code and then the outer codes. Typically, the inner code is not a block code but a soft-decision convolutional-decoded code with a short constraint length. For the outer code, a longer hard-decision block code, frequently Reed Solomon with 8-bit symbols is selected. |
III. CONCATENATED BCH-TCM WITH 8PSK |
| The block diagram of the proposed concatenated scheme is shown in figure 2. BCH codes form a class of cyclic error-correcting codes that are constructed using finite fields. BCH codes were invented in 1959 by Hocquenghem, and independently in 1960 by Bose and Ray-Chaudhuri. The abbreviation BCH comprises the initials of these inventors' names.One of the key features of BCH codes is that during code design, there is a precise control over the number of symbol errors correctable by the code. In particular, it is possible to design binary BCH codes that can correct multiple bit errors. Another advantage of BCH codes is the ease with which they can be decoded, namely, via an algebraic method known as syndrome decoding. In communications, Trellis-coded modulation is applied to solve the conflict of utility efficiency between transmission power and channel bandwidth. TCM is used for data communication with the purpose of gaining noise immunity over uncoded transmission without changing the data rate. The use of TCM also improves system reliability without increasing transmitting power and required channel bandwidth.Trellis Coded Modulation (TCM), pioneered by Ungerboeck has received widespread interest as a bandwidth efficient forward error correction scheme. It has been discovered in the late 1970s and is now used in many systems for modern information transmission, especially in modems. The basic concept of the Trellis Coded Modulation technique is to perform coding onto an expanded modulation signal set. Coding is used to form structured signal sequences with large minimum Euclidean distance. |
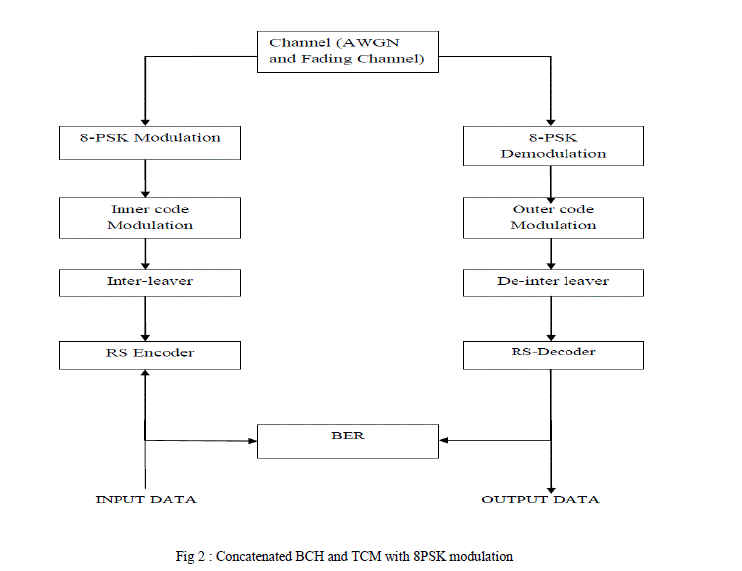 |
| The TCM coding process utilizes signal mapping combining error-correcting coding with modulation. The mapping by the set partitioning technique provides a combination of digital signals used in the modulation. This technique increases the minimum Euclidean distance between the pairs of coded signals; hence the loss from the expansion of the signal set is easily overcome and a significant coding gain is achieved with ECC. This is the reason why TCM technique does not violate the basic trade-off principle between power, bandwidth, and error probability. Therefore, in a bandwidth-limited communication system, without bandwidth enlargement, the redundancy bits are introduced into the signal to achieve good performance of coding gain through the TCM codes. |
IV. SIMULATION RESULTS AND PERFORMANCE COMPARISON |
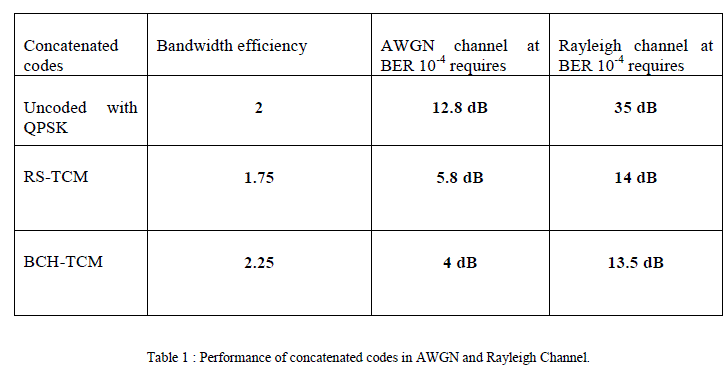
| The performance of concatenated (BCH-TCM) encoder for 8-PSK modulation over AWGN and Rayleigh fading channel were evaluated. Figure 3 shows the Simulated results of BCH-TCM with 8PSK modulation in AWGN channel. Figure indicates that BCH-TCM can only achieve BER of 10-5 with Eb/N0 of 6 dB compared to about 12.8 dB needed for uncoded 4-PSK in AWGN channel. |
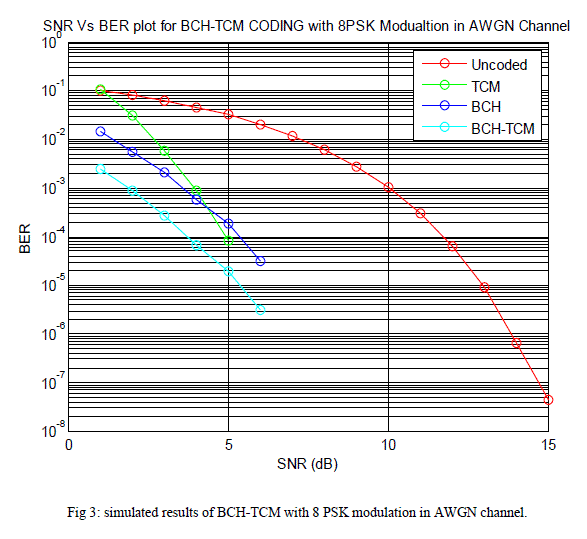 |
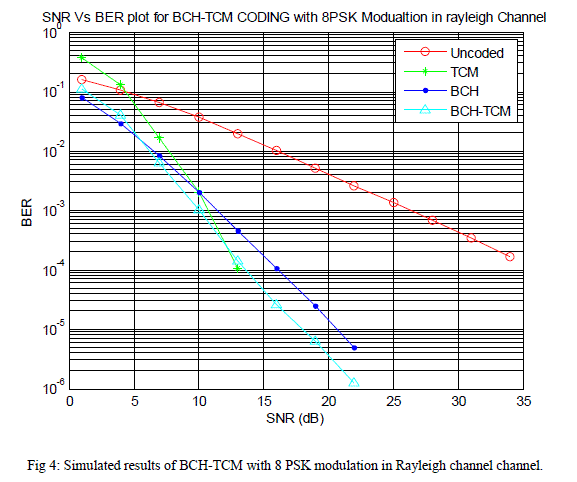 |
| Figure 4 shows the Simulated results of BCH-TCM with 8PSK modulation in Rayleigh channel. Figure indicates that BCH-TCM can only achieve BER of 10-4 with Eb/N0 of 13.5 dB compared to about 35 dB needed for uncoded 4-PSK in AWGN channel. |
 |
V. CONCLUSION |
| In this paper, BCH and TCM concatenated system for 8PSK modulation has been proposed. Simulation results show that the proposed concatenated system provides significant bandwidth efficiency than RS-TCM. The proposed scheme has been compared to uncoded QPSK and RS-TCM. BCH-TCM has superior coding gain in AWGN and Rayleigh channel. |
References |
|