ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Kirankumar K.M1, Dr. Basawaraj2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Current thesis described in this manuscript is an effort to fill a need in the gas turbine industry for a systematic validated computational methodology for conjugate heat transfer problem to give the optimum cooling Channels designee and Channels positioning in gas turbine airfoils to obtain batter cooling rate in the blade. Because ofnature of cooling for turbine airfoils it is deemed to be necessary to include comprehensive numerical study in internal cooling with ribbed channels and investigate heat transfer deduction in channel turns.In this part CFD and conjugate heat transfer solutions are compares against measures surface pressure and heat transfer profile on the C3X turbine blade. The conjugate numerical methodology was employed to predict the metal temperature of a three dimensional gas turbine blade at realistic operating conditions. Numerical results compared with experimental results available in literature in terms of pressure distribution on the blade wall. The present study involves conjugate heat transfer methodology for application to the aerothermal problem of an internally-cooled gas turbine airfoil at realistic operating conditions with MARK-II using CFX 12.1. Meshing was done by HM, with the design environment in mind; attention is given to high-quality mesh generation. Finally CFD results were compared with experimental test casesavailable in the literature.
Keywords |
| CFD, Conjugate heat transfer, Aero-Thermal, Gas turbine. |
I. INTRODUCTION |
| Assessing the life and improving the thermal design of a turbine blade play major roles in all fields where gas turbine engines are utilized. Analyzing the thermal design of a blade design with understanding the complex velocity and thermal boundary layers around the blade predicting highly accurately the blade surface heat load created by the hot gas stream moving over the blade is essential to predicting the corresponding thermal stresses inside the blade.In several industrial applications it is becoming necessary to accompany the computation of flow and associated heat transfer in the fluid with the heat conduction with in the adjacent solids. The coupling of these two models of heat transfer has been identified by the name “conjugate heat transfer”, in the relevant literature. Typical application where conjugate heat transfer effects can become important in cooling of turbine blade. |
| Conjugate heat transfer approach allows the simultaneous solution of the external approach allows the simultaneous solution of the external flow, internal convection and conduction with in the metal blade. The fundamental aim of this technology area is to obtain the highest overall cooling effectiveness with the lowest possible penalty on the thermodynamic cycle performance. Han et al [3] performed two and three-dimensional conjugate analysis of a radially cooled gas turbine blade: the only thermal boundary conditions they imposed were the HTC on the surfaces of the internal coolant flow passages. Manipulation includes movement to new locations, change of size, change of number or spacing, addition to and subtraction from the component. |
II. MODEL FORMULATION |
| The lateral conjugate heat transfer analysis is only concerned about geometry of the blade, cooling holedimension, inlet and outlet property of combust gas, inlet condition of cooling air and material property are from an existing model MARK-II vane. The model is developed in CATIA, meshing in hypermesh and analysis done in CFX. |
| AIRFOIL MODEL: Geometries can be created top-down or bottom-up. Top-down refers to an approach where the computational domain is created by performing logical operations on primitive shapes such as cylinders, bricks, and spheres. Bottom-up refers to an approach where one first creates vertices (points), connects those to form edges (lines), connects the edges to create faces, and combines the faces to create volumes. Geometries can be created using the same pre-processor software that is used to create the grid, or created using other programs (e.g. CAD, CATIA). Geometry files are imported into hypermesh to create computational domain. The Extracted fluid domain of MARK-II vaneHylton et al[5].as shown in Fig.1 |
 |
| MESHING: The multi-topology, unstructured mesh may contain hexahedra, tetrahedral, pyramid, and triangular prism cells in three-dimensional (3D) space.3D hexahedra cell would have all edges meeting each other at right angles, and the perfect 2D triangle cell is equilateral with congruent interior angles of 60o. In addition, the cell aspect ratio and size or density may influence the overall quality of the grid. Extra care is taken to ensure high grid quality and density along solid boundaries. Layers of closely-spaced hexahedra or prism cells are placed near the wall to ensure that the full turbulent boundary layer is resolved, including the narrow viscous sub layer. |
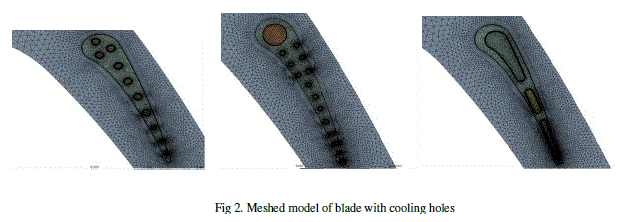 |
 |
III. CFD ANALYSIS |
| Definition of boundary conditions and other parameters, initial conditions, before starting a simulation in CFX, the mesh has to be checked and scaled and modified if necessary. The physical models have to be tackled. This includes the choice of compressibility, viscosity, heat transfer considerations, laminar or turbulent flow, steady or time dependent flow. The boundary conditions have to be clear because they specify the information of the state of the flow in the determined zones: walls, symmetries, inlet air, outlet air, etc. |
BOUNDRY CONDITIONS: |
 |
 |
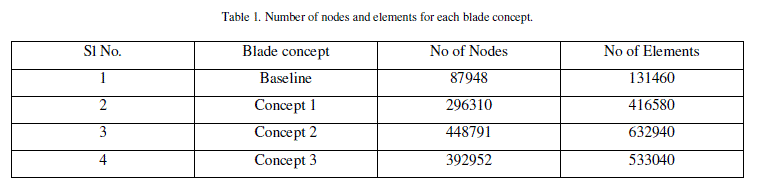
| Four models were considered for this study. The boundary conditions were kept same for all the models and analysis was done. The details of the meshed models are as given in table 1. Resolution of the problem, which is done through iteration until the convergence of the variables is obtained. First of all, the variables of the flow have to be initialized and set to be computed from a certain part specified by the user. In this stage the equations of the flow are solved. The values of the pressures are constantly updated and corrected through iterations. The convergence is checked until it reaches the criterion value set by the user. |
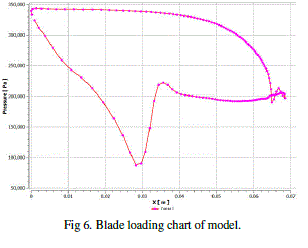
| RNG turbulence model was used for the computation of results in this work. The governing equation used is as given below |
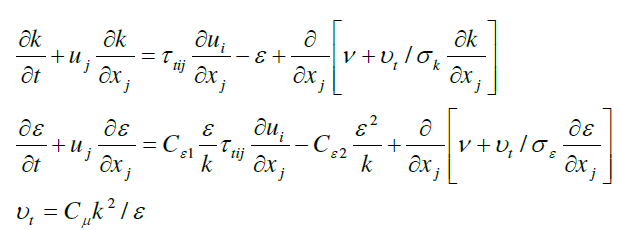 |
| Velocity vectors, path lines. In them, several variables can be analyzed: velocity, pressure, turbulence, forces, density Post Processing or analysis of the results computed. There are lots of choices: Contours, X-Y plots, and others. |
CONVERGENCE CRITERIA: |
| The iterative process is repeated until the change in the variable from one iteration to the next becomes so small that the solution can be considered converged. |
| At convergence |
| All discrete conservation equations (momentum, energy, etc.) are obeyed in all cells to a specified tolerance. |
| The solution no longer changes with additional iterations. |
| Mass, momentum, energy and scalar balances are obtained. |
 |
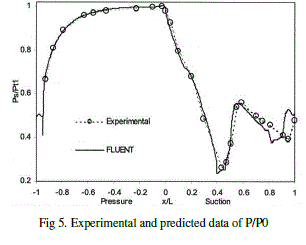
| The predictions exhibit close agreement with the data of Hylton et al.[5], validating the aerodynamic portion of the model. |
IV. RESULTS AND DISCUSSION |
 |
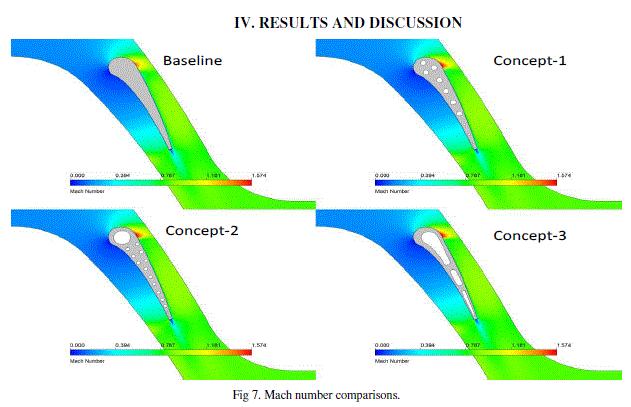
| The comparison between the four models shows no significant change in Mach number which means that there will be no friction losses compared to the base model. |
 |
| Figure 6 Temperature distribution in the metal vane all three concept of constant spanwise coordinate. The ability to pinpoint hotspots and high thermal gradient zones within the airfoil is a great benefit of the conjugate heat transfer method as a design tool. |
 |
 |
V. CONCLUSION |
| A stainless steel turbine vane at near-engine conditions and at subsonic passage flows was tested using 3-D simulation. |
| The predicted midspan temperature distribution on the vane external surface was in reasonable agreement with experimental data |
| The metal temperature everywhere was much closer to the temperature in the passage freestream than the coolant temperature. |
| The greatest thermal resistance in the blade was found to be due to the internal convection. Thus, lowering the resistance of internal convection by increasing the heat transfer coefficient in the cooling channels would result in a sizeable reduction in metal temperature throughout the vane. |
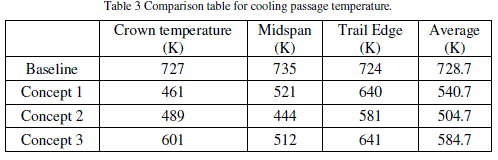
| The results shows that the decreasein temperature by 10% from concept 1 to concept 2 and it increases for concept 3. Hence the concept 2 is considered as optimum for conjugative heat transfer. |
| This was achieved by manipulating the placement of cooling holes in the vanes which resulted in increased turbine efficiency. |
References |
|