ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
D.Pradeepkannan, Dr.S.Sathiyamoorthy
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Conventional PID controller is a simplest well known controller used in almost all process Industries for controlling the process parameters at desired set value. The tuning of these controllers is done by a classical Zeigler Nichols (ZN) tuning. The dynamics of a spherical tank process is nonlinear in nature and it exhibits non linear behavior and time delays between the inputs and outputs. The ZN tuned PID controller parameters does not cope with all operating points as it exhibits different non linear characteristics at various operating points. This paper aims at real time implementation of enhanced PID controller performance for a nonlinear spherical tank process. The idea is to keep the ZN tuned PID values as the base value so as to fine tune these parameters using a Genetic Algorithm approach to obtain the optimal set of tuning values which can cope up with all operating points. The mathematical model is developed by applying the governing mass balance equations and substituting the arbitrary constants. The system identification of the non linear process is done by black box modeling and found to be (FOPDT) First order plus dead time model. The controller performance of the ZN tuned PID controller is fine tuned using GA based PID controller in terms of time domain specification as well as performance indices. Better enhanced controller performance was obtained for a GA tuned PID controller than that of ZN tuned PID controller at all operating points. All the simulations are carried out in Mat lab environment and the real time implementation is done on a single spherical tank setup in LabVIEW Environment.
Keywords |
| PID controller; ZN tuning; Genetic Algorithm; Non linear spherical tank process. |
INTRODUCTION |
| Proportional Integral Derivative Controller has been using in Industrial control applications for a long time. The reasons for their wide popularity lies in the simplicity of design and good performance which includes low percent over shoot and small settling time for slow process Astrom.K.J and Hagglund.T,(1995).According to the survey in 1989, 90 percentage of process industries uses the conventional PID controllers [3].The wide spread use of the PID controller in the Industry is due to their simplicity and ease of retuning online [4].The PID controller is so named because its output sum of three terms, proportional, integral and derivative term. Each of these terms is dependent on the error value ‘e’ between the input and the output. |
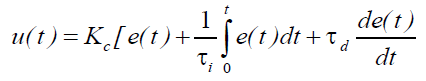 |
| e(t) is the error signal, u(t) is the controller output, Kc is the controller gain, τi and τd are integral gain and derivative gain. Proportional term speeds up the response as the closed loop time constant decreases with the proportional term but does not change the order of the system as the output is just proportional to the input. The proportional term minimizes but does not eliminate the offset .Integral term eliminates the offset as it increases the type and order of the system by one. This term also increases the system response speed but at the cost of sustained oscillations. Derivative term primarily reduces the oscillatory response of the system. It neither changes the type and order of the system nor affects the offset. Determining optimum value of Proportional constants kp,i,d is termed as tuning. Any change in these parameters cause changes in the type, order and response of the system. Thus they play a vital role in obtaining a good controller performance characteristics. There have been a various types of tuning techniques applied for PID controller. One of the oldest is that Zeigler Nichols technique. These techniques may be of Optimization technique or classical technique. Classical techniques make certain assumptions about the plant and the desired output and try to obtain analytically, or graphically some feature of the process that is then used to decide the controller settings. These techniques are computationally very fast and simple to implement, and are good as a first iteration. But due to the assumptions made, the controller settings usually do not cope up with non linear behavior of the process and are unable to give desired response at all operating points which then requires further fine tuning. One of the most successful and oldest classical techniques is Zeigler Nichols method. It was put forward by John Ziegler and Nathaniel Nichols in 1942 and is still a simple, fairly effective PID tuning method. He proposed two methods, one is open loop step response method and the second is closed loop frequency response method. The Ziegler and Nichols first PID tuning method is the techniques made based on certain controller assumptions. Hence, there is always a requirement of further tuning; because the controller settings derived are rather aggressive and thus result in excessive overshoot and oscillatory response. Also the controller parameters are rather difficult to estimate in noisy environment. The second method is based on knowledge of the response to specific frequencies. The idea is that the controller settings can be based on the most critical frequency points for stability. This method is based on experimentally determining the point of marginal stability. This frequency can be found by increasing the proportional gain of the controller, until the process becomes marginally stable. These two parameters define one point in the Nyquist plot. The gain is called ultimate gain Ku and the time period Tp. As the process exhibits non linear behavior at various operating points, this paper aims at fine tuning of the controller settings can be done by computational techniques such as genetic algorithm. This paper is organized as follows. The section 2 describes about literature review of Genetic Algorithm for PID tuning. Section 3 explains about the mathematical modeling of the non-linear spherical tank process. Section 4 describes the Experimental set up and its real time implementation of conventional PID controller and GA tuned PID controller. Section 5 describes the Results obtained for servo operation at various operating points of the tank for both ZN PID controller and GA tuned PID controllers. Finally the conclusion is given in section 6. |
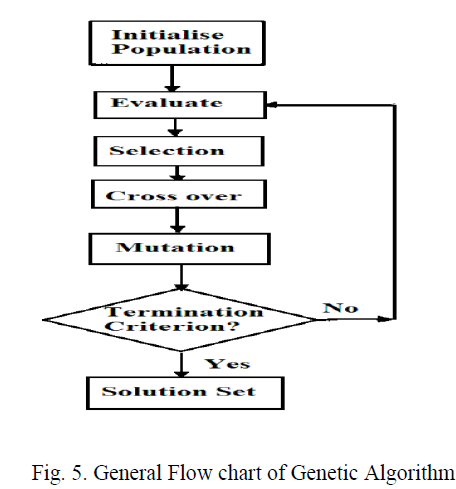
GENETIC ALGORITHM |
| Genetic algorithm (GA) is a search algorithm that explores the search space in a manner analogous to evolution in nature Salami.M and Cain.G(1995). It uses probabilistic rules to search for and change the potential solutions in the search space, using a cost function to analyze the fitness of solutions. GA requires the solution to be represented in a way that is analogous to genes so that the processes that bring about a change in the genes can be used. Usually this is done by representing the solutions in a binary format. GA is very popular in PID tuning and has gained wide applications in control systems Kumar.S.M.G, Jain.R and Anantharaman.N.(2008).Sadasivarao.M.Vand Chidambaram,(2006) uses GA for improving performance of a PID controller used in bioreactor and compared the performance with Ziegler Nichols, Skogestad modification Skogestad.S.(2003) found that GA outperformed both in terms of overshoot, disturbance rejection, gain margin and phase margin. GA has been used in position and speed control of a DC motor NeenuThomas P. Poongodi(2009). SharifianM.B.B.Rahnavard.RandDelavari.H(2012). GA has been used for PID of reverse osmosis Jin-Sung Kim, Jin-Hwan Kim, Ji-Mo Park, Sung-Man Park, Won- YongChoe and Hoon Heo,(2008) and cascade control systems tuning in Sadasivarao.M.V and Chidambaram,(2006). Lot of work has been done in using GA along with other computational techniques. In Kim et al. uses bacteria forage along with GA for PID controller tuning of AVR systems. GA was used with Neural Networks Dolezel, PetrMares,(2009) and with fuzzy logic for developing self tuning methods. |
MATHEMATICAL MODELLING |
| A spherical tank system, shown in figure 1 is essentially a system with non linear dynamics. The spherical tank system has a maximum height of 0.5meter and the maximum radius of 0.5 meter. The level of the tank at any instant is measured by the combination of orifice and Differential pressure transmitter whose output is (4 - 20)mA. This output is compared with the desired set point value of level which will be configured as (4 - 20)mA. The error signal is amplified based on the controller specification. The controller output is used to vary the inflow rate q1(t) of the spherical tank so as to maintain the set point at desired level of the tank. An Electro pneumatic converter is used to convert the controller output of (4 -20)mA in to a pneumatic signal of (3-15) psi so that the final control element will be able to throttle the inflow rate. |
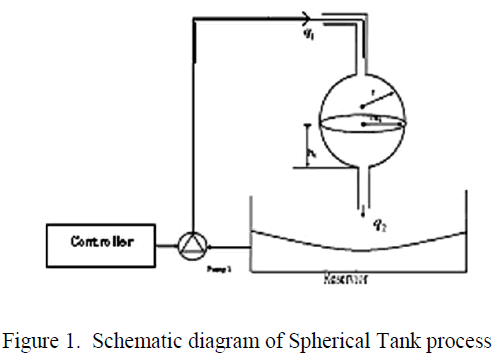 |
| let, q1(t) - inlet flow rate to the tank in m3/sec |
| q2(t) - outlet flow rate of the tank in m3/sec |
| H - Height of the spherical tank in meter. |
| R - Radius of tank in meter (0.5 meter). |
| xo - Thickness of pipe in meter(0.04 meter). |
| Using law of conservation of mass the non-linear plant equation is obtained for the spherical tank, |
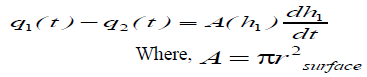 |
| Radius on the surface of the fluid varies according to the level (height) of fluid in the tank. Let this radius be |
 |
EXPERIMENTAL SET UP OF SINGLE SPHERICAL TANK PROCESS |
 |
| The experimental set up of the single spherical tank system is shown in figure 2. The spherical tank is made up of SS316 material which has high corrosion resistance property and has a maximum height and radius of 0.5 meter. Water from the reservoir tank of size 1250mm x 450mm x 450mm is pumped through a Kirloskar make 0.5 HP pump having a discharge of 1500 litres per hour that flows through a Teleline make rotameter having a range (40 - 440)LPH to the spherical tank. The level of the tank at any instant is measured by the Rose mount Differential pressure transmitter having a measurement range of (0-400)mm of water column corresponds to the output range of (4 -20)mA. This output is compared with the desired set value of level which will be scaled in the control law as (4 -20)mA. The error signal is also in the range of (4-20)mA which is then amplified based on the controller specifications. This output is used to vary the inflow rate q1(t) of the spherical tank with the use of an ABB make Electro pneumatic converter which converts the output of (4 -20)mA in to a pneumatic signal of (3-15) psi so that the Equal percentage control valve will be able to throttle the inflow rate. The controller parameters are determined for both ZN tuned PID Controller as well as GA tuned PID controllers. The values of kp, ki, kd for ZN tuned PID are found to be 0.33, 0.036, 0.7623 respectively. An USB 6009 NI Data acquisition card is use to communicate the data from the transmitters to the PID controller block of LabVIEW program both for ZN and GA tuned control algorithm to perform its operation for a given step change in inflow rate qi, and the corresponding steady state response is obtained as follows. |
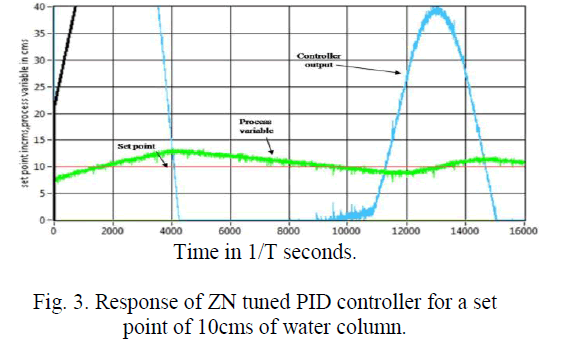 |
| It is evident from the response that the ZN tuned PID controller output could track the set point at an operating point of 10cms of water column with a settling time of 13.15seconds and with minimal overshoots where the sampling rate T is 32samples per second. |
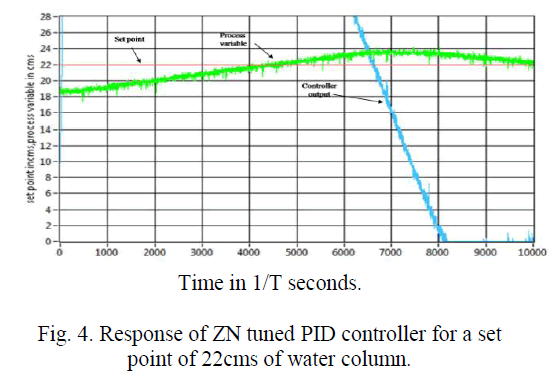 |
| It is evident from the response that the ZN tuned PID controller output could track the set point at a different operating point of 22cms of water column with a settling time of 8.22seconds and with minimal overshoots where the sampling rate T is 32samples per second. |
| A. GA based PID controller |
| Genetic algorithms (GA) are an evolutionary optimization approach, which are an alternative to traditional optimization methods. GA is one of the most appropriate methods for complex non-linear models where location of the global optimum is a difficult task. GA follows the concept of solution evolution by stochastically developing generations of solution populations using a given fitness. Genetic algorithms are a probabilistic search approach, which are founded on the ideas of evolutionary processes. The GA procedure is based on the Darwinian principle of survival of the fittest. An initial population is created containing a predefined number of individuals, each represented by a genetic string. Each individual has an associated fitness measure. The concept that the fittest best individuals in a population will produce a fitter offspring is then implemented in order to reproduce the next population. Selected individuals are chosen for reproduction at each generation, with an appropriate mutation factor to randomly modify the genes of an individual, in order to develop the new population. The result is another set of individuals based on the original subjects leading to subsequent populations with better fitness and those with lower fitness will naturally get discarded from the population. (Goldberg 1989; Lewin 1994, 1996).For most applications of genetic algorithms to optimization problems, the real coding technique is used to represent a solution to a given problem. In real coding implementation, each chromosome is encoded as a vector of real numbers, of the same lengths as the solution vector. According to control objectives, three parameters Kp, Ki and Kd of a PID controller are required to be designed in this research. For a given problem with three decision variables, this paper adopts a real-valued vector [x1, x2, x3] as a chromosome to represent a solution to the problem. |
 |
| B. Tuning of GA-Based PID Controller |
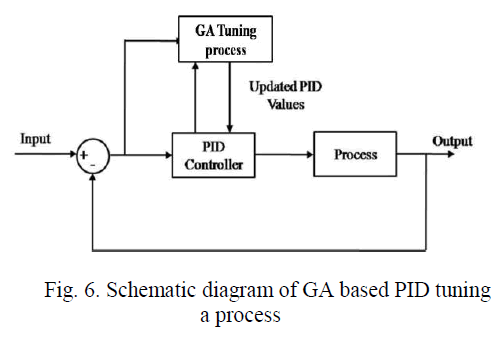
| Genetic Algorithm can naturally be applied to the optimal-tuning of PID controllers as a mathematical means for optimization. The role of the PID controller in a system is to drive the output response to track the set point within minimum settling time. Obviously, the parameter settings of the PID controller should be fine tuned so as to meet the requirements. Optimization of PID controllers firstly needs design the optimization goal, and then encode the parameters to be searched. Genetic operator is running until the stop condition is satisfied. The decoded values of the last chromosome are the optimized PID controller parameters. |
 |
| Initially a chromosome is randomly generated. The chromosomes are candidate solutions to the problem. The fitness values of all chromosomes are evaluated by calculating the objective function (ISE) in decoded form. Hence, based on the fitness of each individual, a group of the best chromosomes is selected through the selection process. The Genetic operators, crossover and mutation, are applied to this surviving population in order to improve the next generation solution. The process continues until the population converges to the global maximum or another stopping criterion is reached. The GA optimization tool in matlab is used to fine tune the PID parameters so as to obtain the desired performance characteristics. The following figure 7 shows the Optimization wizard for GA tuned PID controller. The fitness function syntax is developed as a function and saved with a file name Sphh. Then the other parameters such as lower bounds, upper bounds, number of variables, Initial population, Initial range, number of iteration, Mutation factor, Cross over factor and selection function are given to the wizard. On running the program, it determines an optimal set of tuned parameters for PID controller as kp =6.997,I=6.144sec and d =1.998sec. |
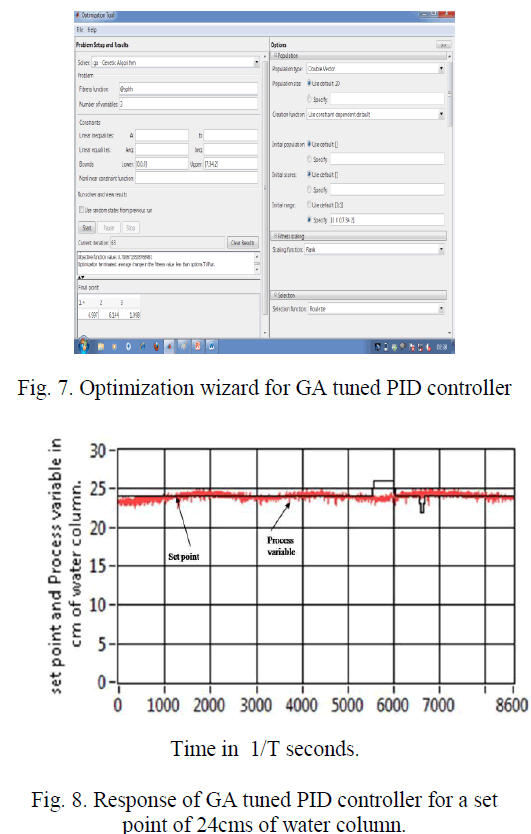 |
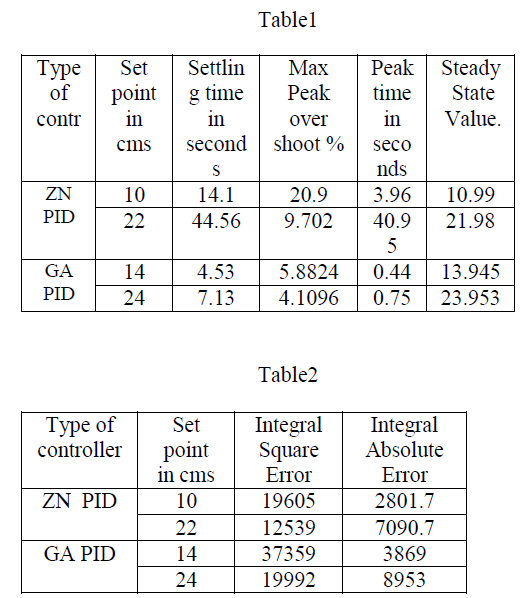
| It is evident from the response that the GA tuned PID controller output could track the set point at a different operating point of 24cms of water column with a settling time of 7.13seconds and with smooth response and no overshoots where the sampling rate T is 32samples per second. A small disturbance is being provided between the time instances 5000,6000,and 7000 so as to ensure robustness, the controller ensures disturbance rejection and it keep tracks the set point value as desired. |
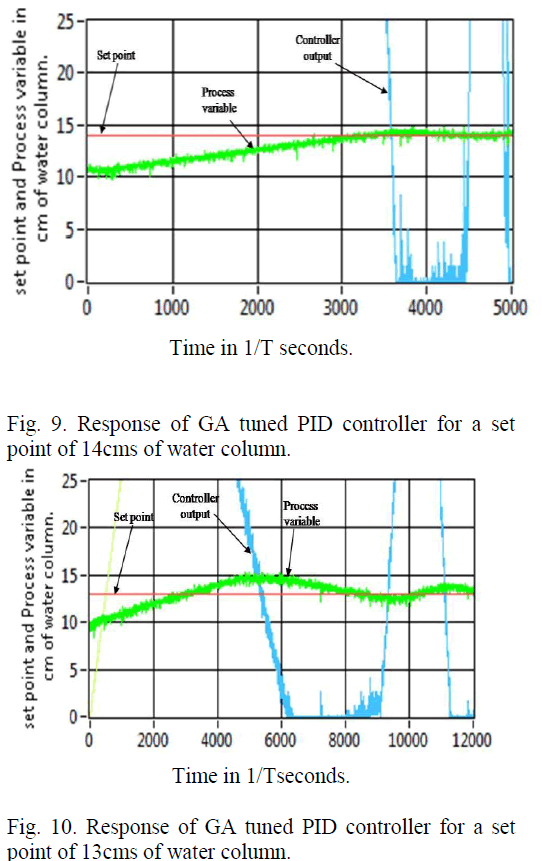 |
| It is evident from the response that the GA tuned PID controller output could track the set point at a different operating point of 14cms of water column with a settling time of 4.53seconds and with smooth response and no overshoots where the sampling rate T is 32samples per second. |
RESULTS AND DISCUSSION |
| An unit step response of ZN tuned PID controller and GA tuned PID controller is obtained for servo operations and their performance characteristics are compared in terms of time domain specifications such as rise time ,peak time, peak over shoot, steady state value etc., and performance indices such as ISE and IAE. Table 1 and table 2 show characteristics of time domain specification and performance indices such as ISE and IAE of ZN tuned PID controller against GA tuned PID Controller. |
 |
CONCLUSION |
| GAPID controller can cope up with tank non-linear characteristics at various operating points such as 14, 24centimeters of water column in the spherical tank. Conventional controller based on Ziegler Nichols tuning response is outperformed by GAPID controller with less overshoot and lesser settling time, peak time etc.,. GA tuned PID controller is the basic evolutionary computational method which provides a better satisfactory results as tabulated. The author limited his work with GA based tuning alone, further the controller can be tuned by other soft computing techniques and implemented in real time so as to compare their performances. GAPID controller can also be applied for other non linear processes such as Continuous stirred tank reactor, Yeast fermentation process, Bio reactor etc to obtain better controller performance characteristics. |
References |
|