ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Bhargob Deka1, Syed Nafifur Rahman2, Pranjal Tamuly3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This study quantifies the influence of strong ground motion duration (SGMD) of aftershocks on the cumulative damage caused to a RC frame structure. Understanding the effect of ground motion duration on cumulative damage and failure mechanisms will bring us one step closer to preventing future earthquake-induced collapses and can also aid in improving Building code. In order to study the effects of Duration, the other time-frequency characteristics i.e. amplitude and frequency content are kept similar. A realistic nonlinear numerical structure is modelled in SAP2000 in order to incorporate cyclic deterioration of strength and stiffness. Two sets of data are considered i.e. longer duration (>40sec) and shorter duration (<25 sec) and for each set of data cumulative damage are calculated using modified Park and Ang Damage Index. It is seen that in general longer duration data sequence causes more damage than shorter duration sequences because of longer cycles of loading
Keywords |
| Damage Index, Long Duration, Cumulative Damage, Mainshock, Aftershock. |
INTRODUCTION |
| The important parameters that characterize a ground motion are namely amplitude, frequency content and duration. Amplitude (as characterized by PGA of the ground motion), predominant frequency and strong ground motion duration are the time-frequency characteristics of a strong ground motion data. However these parameters cannot solely be responsible for the damage caused to a structure though it may have a direct impact on the cumulative damage of the structure. The correlation between SGMD (Strong Ground Motion Duration) and the cumulative damage to a structure is not a clear picture. For example, in 2009, Krawlinker derived a positive relation between number of cycles i.e. SGMD and structural damage based on experimental testing. On the other hand, the study carried out by Iervolino (2006) finds no such relation between SGMD and probability of damage and states that duration content of the ground motion is statically insignificant to displacement ductility and cyclic ductility demand. A study carried out by Hancock J.(2006) concludes that when cumulative energy is considered to measure structural damage, a positive correlation is seen between SGMD and damage induced whereas employing damage measures using maximum response generally do not find any strong correlations between duration and damage (Hancock J.,2006). |
| The main challenge in studying the effect of duration has been the difficulty in isolating the effect of ground motion duration from the effects of other ground motion characteristics like amplitude, spectral shape etc.(e.g., Baker, 2006). Hence, it is necessary to ensure that all other time-frequency characteristics are kept similar i.e. Fourier spectral shape, amplitude and predominant frequency in order to understand the sole effect of duration on the cumulative damage of the structure. Moreover, cyclic deterioration of strength and stiffness has to be incorporated in the structure and is essential to accurately estimate collapse and provide conclusive evidence of the correlation between SGMD and structural damage. (Hancock J., 2006). |
| In order to quantify the damage of the structure, Modified Park and Ang Damage Index is implemented because of its worldwide popularity as it takes into account the effects of both displacement ductility demand and hysteretic energy demand in low-cycle-fatigue, and therefore is a demand parameter suitable for PBSD. For ex. Datta D. and Ghosh S. (2008), generated UHS for Park-Ang damage index which are very good tools for probabilistic hazard estimation as intended in PBSD of an elastic-perfectly plastic oscillator. In 2008, Craifaleanu I. G., Lungu D., generated damage spectra, based on the Park-Ang damage index, DM, for Vrancea events with moment magnitude larger than 6.0. |
| The main objective of this study is to highlight the effect of long duration aftershock ground motion over the cumulative damage to a structure. In order to incorporate cyclic deterioration of stiffness and strength, a realistic nonlinear numerical structure is modelled where plastic hinges at the frame elements are modelled as link elements. Spectrally equivalent aftershock ground motions having similar PGA are employed to account for the correlation between SGMD and cumulative damage. A Portal RC Frame Structure is modelled in SAP2000 and Non-linear Direct Integration Time History Analysis is carried out. |
II. MODELING OF STRUCTURE |
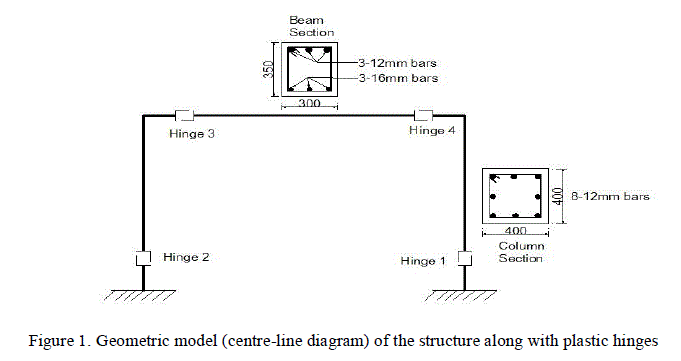 |
| Geometric Modelling: A 2D one bay one storey RC frame structure is modelled in SAP2000 (CSI, 2011) as shown in the figure 1.The columns are fixed at their supports at the base and beam column joints are considered rigid. Beam and column sections are modelled with the help of SAP2000 (CSI, 2011) section designer toolbox. The dimensions of the beam are 300mm (width) and 350mm (depth) considering a clear cover of 25mm on all sides and those of column are 400mm (width) and 400mm (depth) with a clear cover of 40mm on all sides. The beam and column sections near the joints are provided with 8 mm mild steel stirrup of yield strength 250 MPa as per IS 1786-2008 (BIS, 2008), with a spacing of 75mm centre to centre. |
| Material Modelling: Characteristic strength of concrete is considered to be 20 MPa as per IS: 456-2000 (BIS, 2000) and yield strength of steel is considered to be 415 MPa as per IS: 1786-2008 (BIS, 2008). Mander confinement model (Mander et al., 1998) is used in concrete modelling of core concrete |
| Modelling of Plastic Hinge: Plasticity in RC members is assumed to be lumped at specific locations denoted as plastic hinges. Plastic hinges are assumed to form at a distance equal to one-half of the average plastic hinge length lp from the member ends (Kaushik et. al, 2009). Lp was calculated using the following expression (Paulay and Priestley 1992) |
| lp= 0.08L + 0.022dbfy(m) (1) |
| Where, L = length of initial contraflexure point from the ends; db= diameter of longitudinal steel in m; and fy= yield strength of longitudinal steel in MPa. Takeda hysteretic model is used to define the hysteretic character to the plastic hinge. Monotonic moment rotation relationships of beam and columns are assigned to the hinges, obtained from monotonic moment curvature relation and plastic hinge length of the respective element. |
| Loads Applied: The structure is subject to dead load of self weight of the structure and imposed gravity load of 25 KN/m is applied to the beams. The earthquake load is applied in the form of time history earthquake ground motion. |
DURATION METRIC |
| In many literatures, a number of definitions for SGMD have been provided. The effect of SGMD on the structure will depend on the duration metric chosen. For this study, significant duration metric has been chosen to quantify SGMD of the ground motion data taken. It has been seen in previous studies that significant duration metric is the most robust metric of ground motion duration for Performance based Structural Assessment (Chandramohan et al., 2013). |
| Significant Duration is the time interval over which a specific percentage of the total energy represented by the integral ∫ ïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿý is accumulated, where a represents the ground acceleration (commonly used ranges for the accumulated energy are 5% to 95% and 5% to75%). This Study therefore uses t5-95 to quantify ground motion duration considering SGMD to be the portion where 90% of the input energy is accumulated. |
CLASSIFICATION OF SPECTRALLY EQUIVALENT SET OF DATA |
| To study the effect of time frequency characteristic on structural damage the aftershock ground motions are classified according to their frequency content. For this Fast Fourier Transformation of aftershock ground motion is carried out to convert it from time domain to frequency domain characteristics. Based on the predominant frequency and shape of the Fourier spectra the similarity in frequency content is established. Frequency content of the aftershock ground motions are kept similar in order to study the effect of duration of aftershock in damage of the structure. |
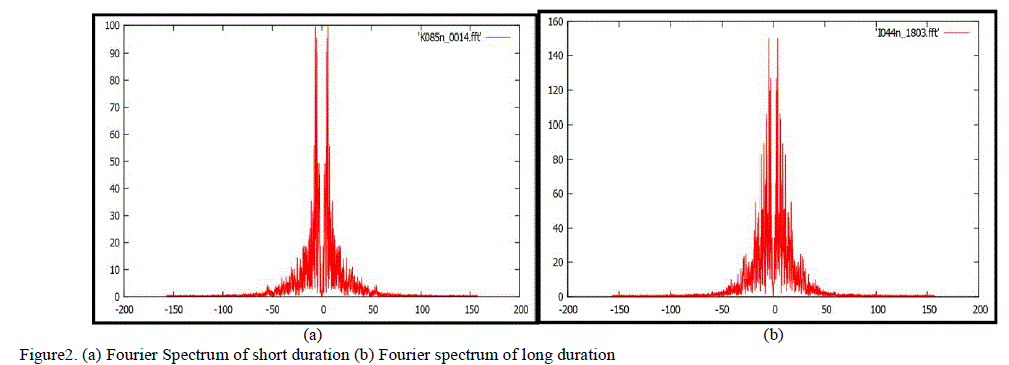 |
| The ground motion data which are used in this study are taken from SCCWB, (1999) as shown in the following table |
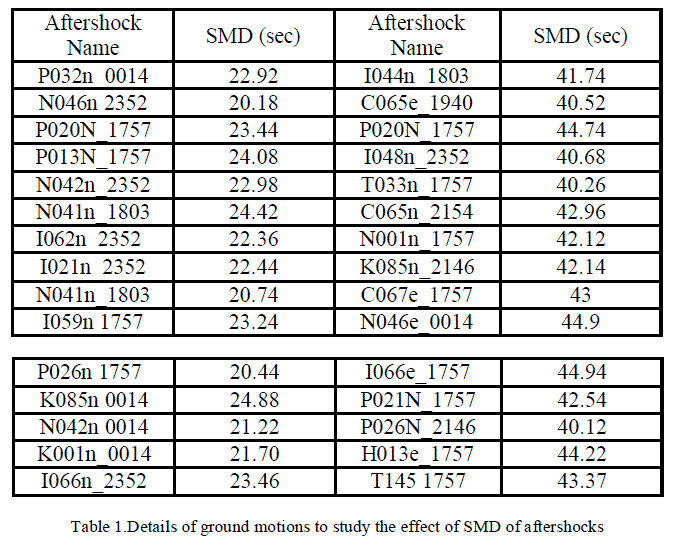 |
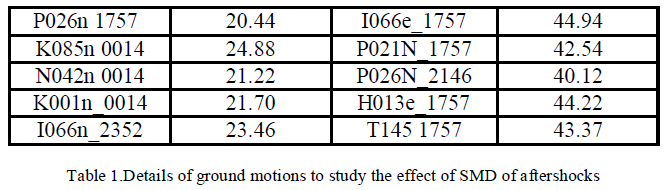 |
III. DYNAMIC ANALYSIS OF STRUCTURE |
| A non-linear Direct Integration Time History analysis is carried out for the RC Frame Structure using the Finite element package SAP2000. Quantification of Damage in the structure is done using Modified Park and Ang Damage index (Kunnath et al., 1992). The local damage index is given by the following relation: |
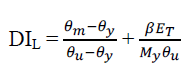 |
| Where DIL is the local damage index, ïÿýïÿýïÿýïÿý is the maximum rotation attained during the time history loading, ïÿýïÿýïÿýïÿý is the ultimate rotation capacity of the section, ïÿýïÿýïÿýïÿý is the yield rotation at unloading, ïÿýïÿý is a strength degrading parameter (taken as 0.15). My is the yield moment of the section and ET is the dissipated hysteretic energy. |
| In the present case, the global damage index is a weighted average of the local damage indices and the dissipated energy is chosen as the weighting function. The global damage index is given by the following relation: |
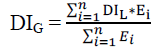 |
| Where DIG is the global damage index, DIL the local damage index, Ei the energy dissipated at location I and n the number of locations at which the local damage is computed. |
| It is ensured that the Damage index calculated at the end of the Mainshock is equal to 0.6 and the cumulative damage occurring due to mainshock-aftershock sequence is noted in each of the cases. |
IV. RESULTS AND DISCUSSIONS |
| The damage index is calculated for each of the two sets of aftershock data viz. longer duration (SGMD > 40sec) and shorter duration (SGMD < 25 sec) having similar predominant frequency at the same level of peak ground intensity. Same Mainshock is taken for each of the cases so that the induced damage at the end of mainshock is same for each of the cases and the PGA of mainshock is scaled until D.I. at the end of mainshock alone is equal to 0.6. The PGA of the aftershock ground motion is scaled to 0.8 times of mainshock PGA to maintain consistency in PGA in each of the cases. The hysteretic energy is given by the area under the plot of Moment vs. Rotation. The Hysteresis loop of two cases from each set is shown in fig. 3 (a) & 3 (b). |
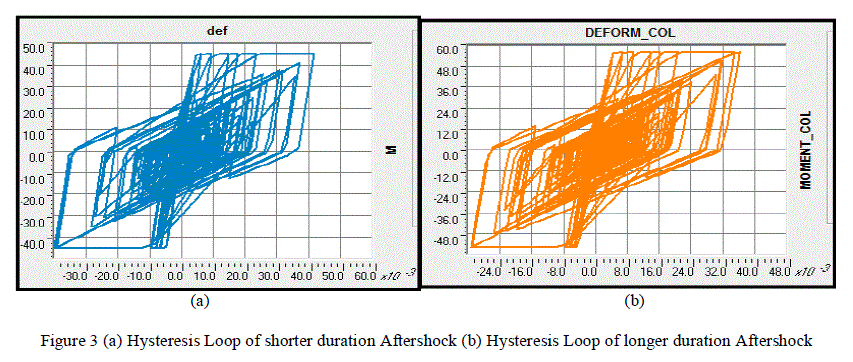 |
| It is seen that because of longer cycles of loading in case of longer duration ground motion, the area of the hysteretic loop comes out to be greater as compared to shorter duration. Hence the hysteretic energy demand is larger in former case which results in more cumulative damage in the structure. |
| To study the effect of duration, two sets of ground motions are selected based on strong ground motion duration. The first set contains 15 aftershocks of duration less than 25 sec and second set contain 15 aftershocks of duration greater than 40 sec. The mainshock damage is kept constant (DI=0.6) for all the cases and the cumulative damage occurring at the end of the mainshock aftershock sequence is calculated. |
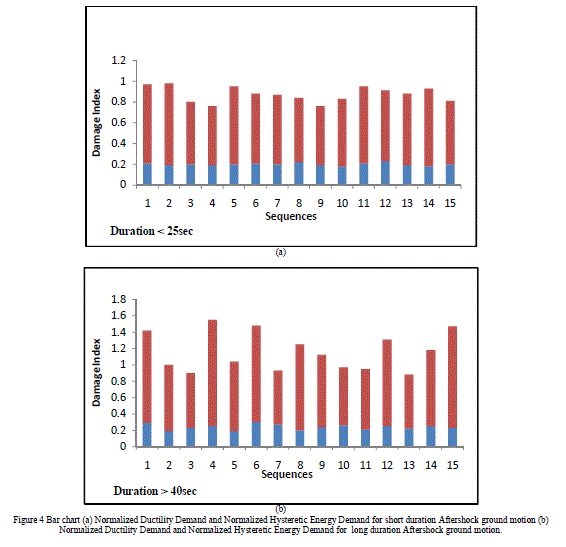 |
| From Fig. 4 it can be easily said that the global damage index is directly proportional to the duration. The aftershocks having duration greater than 40 sec causes more damage than the aftershocks of duration less than 25 sec. Further it is seen that the ductility demand for both cases are similar and it can be said that the ductility demand is mainly depends on the mainshock characteristic which is same for all the cases in this study. |
V. CONCLUSIONS |
| This paper presents the results of an analytical investigation aimed at evaluating the cumulative damage of a portal RC frame structure subjected to longer and shorter SGMD of aftershock. From the results obtained in this investigation, the conclusions are drawn as follows: |
| It can be concluded that a definite correlation exits between SGMD and Cumulative Damage induced in a structure. In general, longer duration aftershock data causes more damage to a structure than a shorter duration. Long duration records are associated with larger number of cycles of loading and impart more energy to the structure. As a result, cumulative damage induced to a structure is found to be higher on being subjected to long duration ground motion having same intensity and predominant frequency as a short duration ground motion. |
| There is no correlation between SGMD and the maximum inelastic deformation of the structure represented by Ductility Demand which more or less remains similar in both the sets of data considered in this study. It is the Energy Demand that signifies the positive correlation between SGMD and damage. Hence, Ductility Demand as a single index for measuring the structural global performance is not sufficient to reflect the damage state of the structure. |
| In the present study only one 2D frame and a single aftershock hazard level (relative to the preceding main shock) have been considered for numerical analysis. A more comprehensive study by varying structural properties and aftershock hazards (including their numbers in a sequence) is needed to provide more insight on the effect of time-frequency characteristics on aftershock induced structural damage. |
References |
|