ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
V. Hema1, M. Ganaga Durga*2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Remote data integrity checking is a decisive technology in cloud computing. Recently, many researchers focus on providing data dynamics and public verifiability. To address users' security concerns, the proposed paper provides a solution to enhance the data integrity and privacy. In this paper we propose a data correctness scheme in which a Third Party can audit the data stored in the cloud and assure the customer that the data is safe. This paper calls upon the Number theory based systems such as Residue Number System and Chinese Remainder Theorem to guarantees not only correct data possession but it also assures retrievability upon some data corruptions. This paper also proves the data owner that a target file is intact, that is, the client can retrieve the entire file from the server with high probability. This scheme shows the correctness and the probability of hacking the data and is eliminated. Based on theoretical analysis, we demonstrate that the proposed protocol has a provably secure and highly proficient data integrity checking measure.
Keywords |
| Cloud Computing, Data Integrity, Third Party Auditor |
INTRODUCTION |
| Cloud Computing appears as a computational paradigm as well as distribution architecture and its main objective is to provide secure, agile, convenient data storage and net computing service, with all computing resources visualized as services and delivered over the Internet. It rapidly provisioned and released the resources with minimal management effort or service provider interaction. Cloud is the long dreamed vision of computing as a utility, can remotely store the sensitive data into the cloud so as to benefit from the on-demand high quality applications and services from a shared pool of configurable computing resources. By data outsourcing, users can be comforted from the burden of local data storage and maintenance. However, the fact that users no longer have physical control of the possibly large size of outsourced data makes the data integrity protection in Cloud a very tough and potentially frightening task, especially for users with constrained computing resources and capabilities. Thus, the auditability for cloud data storage security is of critical importance so that users can resort to an external audit party to check the integrity of outsourced data when needed. |
| A Third Party Auditor (TPA) is introduced to provide the guarantee that communicating parties are who they declare to be and have been scrutinized to hold fast to the strict requirements. TPA is an ideal security facilitator in a distributed cloud environment required for launching secure interactions between cloud client and cloud server. TPA also has the capabilities that a common user does not have, for periodically auditing the outsourced data. The proposed paper assesses cloud security by identifying exclusive security requirements and attempt to present a viable solution that eliminates the potential threats. The proposed paper calls upon cryptography, specifically Public Key Algorithm in concert with Number Theory, to ensure the integrity and confidentiality of involved data and communications. |
| This paper presents a Proof of Retrievability [POR] scheme, which ensures the correctness of data, within which essential trust is maintained. To support efficient handling of multiple auditing tasks, we further explore the technique of Residue Number System and Chinese Remainder theorem to extend our main result into a multi- user setting, where TPA can perform multiple auditing tasks periodically. This scheme which gives a proof of data integrity where the customer can employ to check the correctness of his data in the cloud. This proof can be agreed upon by both the cloud and the user and can be incorporated in SLA. Extensive security and theoretical analysis shows the proposed schemes are provably secure and highly efficient. |
| The rest of the paper is organized into 5 sections. Section 2 describes the concept of Residue Number System. Section 3 describes the concept of Chinese Remainder Theorem. In Section4, Related data integrity works were reviewed. Section 5 illustrates the proposed system. Finally section 6 concludes the paper. |
RESIDUE NUMBER SYSTEM |
| Residue Number System (RNS) [15], in contrast with other Number System is a non-weighted, non-positional number system. RNS can be represented completely by specifying its base. However, RNS does not have a single fixed radix. The RNS bases are represented by N-tuple of integers {m1, m2, ... , mn} where each of these bases is called a modulus. RNS obeys the following form |
 |
| where, x is an integer number represented in residue form. The residue representation is also an N-tuple {r1, r2, ... , rn}defined by a set of N equations. qi is an integer chosen in such a way that . qi can be thought of as the integer value of x/mi. The quantity ri is the least nonnegative integer remainder of the x/mi designated as the residue of |x|mi. The integer ri is the i-th residue digit of x. Residue Number System applied on finite ring and the moduli of the system have to be pair wise relatively prime integers, (i.e.) no two modulus have a GCD greater than 1. This condition is needed to have a huge finite ring made up of smaller sub-rings. Each sub-ring is defined by modulus used in the system. A finite ring is a set of finite elements over which modular addition and modular multiplication operations are defined. So in RNS, the result of the system must also exist within the ring defined by the system and the finite ring of the system has the elements {0, 1, 2, ...., M-1}. Where |
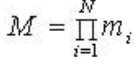 |
| M is a measure of dynamic range of the system and the interval [0, M-1] is called the legitimate range of the RNS. In order to represent negative numbers, the dynamic range (M) of the system is defined as follows: |
| • If M is odd, the dynamic range of RNS becomes |
| [-(M-1)/2,(M-1)/2] |
| • If M is even, the dynamic range of RNS becomes |
| [-M/2, (M/2-1)] |
| Within this dynamic range every number can be represented by a unique set of residues. Each integer number x, in this dynamic range is mapped onto the legitimate range and represented as an N-tuple of residue digits {r1, r2, ...., rn}, where ri = x mod mi for x in the positive half of the dynamic range and ri = mi – x mod mi, for x in the negative half of the dynamic range. |
| The most important concern in designing RNS systems, is the choice of moduli. The efficient choice of the moduli guarantees the most efficient outcome such as speed, hardware etc. The moduli should be relatively prime and as small as possible. The product of the moduli should be large enough so as to offer the required dynamic range for the particular system. It should create a balanced decomposition of the dynamic range which means the difference between the numbers of bits of different moduli should be as small as possible for achieving optimal parallel performance. |
CHINESE REMAINDER THEOREM |
| The Chinese Remainder Theorem (CRT) is the theorem that enables the conversion of residues back into Decimal form. Using this theorem, residues {r1,r2,..., rn} of a number x, can be converted back into x, provided the greatest common divisor of any pair of moduli is 1. The theorem can be expressed as: |
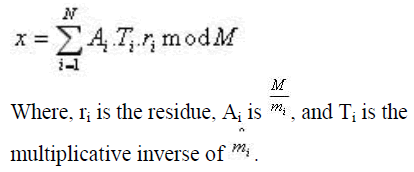 |
RELATED WORKS |
| Cloud computing has recently been recognized as one of the most emerging technology. A significant amount of research has been carried out to explore different areas in cloud computing. However, it also brings new challenges in creating secure and reliable data storage and access facility over insecure service providers. The integrity of data stored in the cloud archive is one of the challenges to be addressed before the novel storage model is applied widely. |
| Data Integrity proofs in cloud storage by Sravan Kumar provides a scheme for static storage of data [2] with bare minimum costs and less effort. To ensure confidentiality, integrity and authentication of the information, a trustworthy service based on trusted encryption scheme is provided with rigid access controls and scheduled data backups. Juels described a formal “proof of Retrievability” model for ensuring the remote data integrity. Their proposal combines spot-checking and error correcting code to make sure both the possession and retrievability of files on archive service systems. An improved method [4] for Proof of Retrievability is presented based on embedding crafted meta data into the original file F and verify its correctness. This scheme comes with limited encryption process. |
| Shacham built a model based on random linear functions which enables unlimited number of queries and requires less communication overhead. Bowers proposed an improved framework for POR protocols that generalizes both Juels and Shacham’s work. Later in their succeeding work, Bowers extended POR model to distributed systems. Merkle Hash Tree Technique [5] is also introduced for Authentication and integrity issues in cloud, However, all these schemes are focusing on the static data. A Traditional RSA algorithm [7] based scheme is introduced to maintain the integrity of the data storage, but it uses the tedious factorization process which slow down the encryption and decryption process. |
| A challenge-response protocol [9] for dynamic data storage is designed to determine data correctness and also locate the possible local errors. Another Proof of Retrievability approach is designed, which uses special blocks called “Sentinels”, that are randomly embedded into the data file for the purpose of detecting the modification of the server data. An improved POR Scheme based on verifiable homomorphic authentication using BLS signatures is used to provide the proof for the data in the storage. |
PROPOSED SYSTEM |
| The objective of this paper is to present a remote data integrity checking protocol based on Number Theory with the support of public auditability. Thus, enabling public auditabililty for cloud data archive, security is of vital importance so that client can resort to an external audit party to check the correctness of the outsourced data periodically. Third party auditor sets the bounded query scheme with the server based on the service level agreement (SLA) made between the client and the server. Using this scheme, TPA performs the periodical integrity checking. TPA efficiently audits the cloud storage without demanding the local copy of data and does not produce burden to the user. TPA also brings in no new vulnerabilities towards client data privacy. |
| In this system, client handover the encrypted file F’ to the TPA and stores only a single cryptographic key irrespective of the size of the data file F. Client encrypt the data file F using Number Theory based RSA Algorithm, which is used to secure data while it is being transferred in and out of the cloud or stored in the provider’s premises. For file decryption, client uses Chinese Remainder theorem based RSA algorithm, which reduces the decryption time (i.e.) four times faster than traditional RSA algorithm [7]. In order to improve the effectiveness of the proposed protocol, tiresome factorization process is replaced by modular squaring and modular multiplication process. |
| So the average decryption time for traditional method is about 0.16 sec per decryption whereas CRT based RSA method requires only 0.046 sec per decryption, giving Speedy original Data. The CRT version of decryption requires the prime’s p and q as well as the decryption exponent d, so this might seem to be an extra source of insecurity. However, it is used to factor the modulus n. |
| There is no security is lost in using this method. Thus, cost complexity involved in integrity checking process is less compared to the existing protocol and also applicable for all kinds of cloud models. |
| A. POR Scheme for verification of validity of data |
| POR scheme consists of two phases. One is preliminary phase and the other is inspection phase. The first phase include the generation of metadata based on Residue Number System(RNS). The second phase deals with issuing a challenge to the server and getting a response and checks the correctness of the data. |
| 1. Preliminary Phase |
| The File F’ consists of n file blocks. Each block comprises m bits of data. The k bits of each block selected for crafting the meta data. TPA generates the meta data using RNS algorithm and stores only the residue set {r1,r2,r3} of the selected cipher text. The algorithm and working principle are discussed below. The following figure shows the process of preliminary phase. |
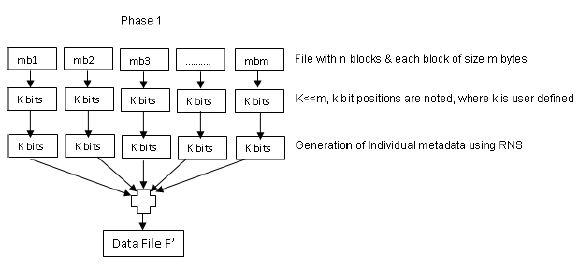 |
| Algorithm for Meta Data Generation : |
| Divide the data file to be stored in the archive into n blocks. |
| Divide the data file to be stored in the archive into n blocks. |
| For every data blocks in encrypted file F’, generate the metadata by using the following : MD = i+j * (cipher value * r1) in the File F’ Assume the moduli as m1,m2.. mn and the residues can be calculated using the following formulas. Let the residue for a decimal x for the moduli set as { m1, m2..mn}, |
| r1=|x|m1, r1=|x|m2…. Rn=|x|mn |
| Append the metadata into the blocks of the encrypted file F’ |
| Finally, upload the File F’ to the storage archive. |
| Inspection Phase |
| If the TPA wants to verify the integrity of the file F’, it throws a challenge to the archive and ask it to respond. TPA send the message like <block info(i,j), residue set and moduli set> to the server for challenge. Server based on the information given by the TPA, computes the following |
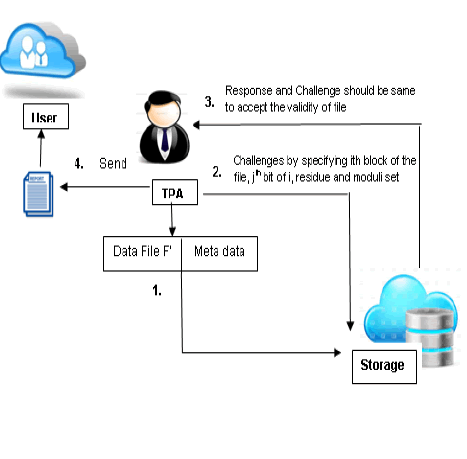 |
| functions and calculates the MD and report to the TPA. The following figure shows the process of inspection phase. |
| 1) The dynamic range M=m1,m2..mn can be calculated using A(1)=M/m(1), A(2=M/m(2),.. A(n)=M/m(n). |
| 2) The multiplicative inverse can be computed using the following formula. Let T(1),T(2)… have to be derived from the following congruence as |
| A(1).T(1) ≡1 mod m1, A(2).T(1) ≡1 mod m2, … A(n).T(n) ≡1 mod mn. |
| 3) Using CRT, the decimal number can be found by using the following formula |
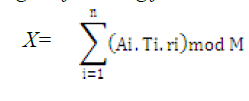 |
| 4) It calculates the MD and response to the TPA. |
| Working principle of the algorithm : |
| Phase 1 |
| For example, the Message(M) to be encrypted is “KEYS”. Using the number theory based RSA Algorithm, encrypt it as C=175 115 029 171. For the cipher value 029, the metadata is generated as follows. |
| Assume {3,5,7} as moduli set. The Residue can for the value 029 is {2,4,1}. Meta data(MD) can be calculated using the formula, MD=i+j*(cipher value * r1, where i be the block number and j be the byte number. So MD=290 is saved as the meta data. |
| All the meta data bit blocks are generated using the above procedure and appended to the file F’ before storing it at the cloud archive. |
| Phase 2 |
| Assume the residue and moduli set given by the TPA as ri={2,4,1} and mi={3,5,7}. The dynamic range(M) can be 3*5*7. (i.e.) M=105. |
| The Ai’s can be find out using: Ai=M/mi (i.e.) A1=35, A2=21 and A3=15. Let T1, T2 and T3 are the multiplicative inverse of A1, A2, and A3. So T1=2, T2=1 and T3=1. |
| By applying the Chinese Remainder Theorem[CRT], X=(35.2.2+21.1.4+15.1.1) mod 105, so X=29.Then MD= 2+3*(29*2) is report the TPA for Verification. |
| The challenge and the response are compared and if the result is true, the TPA accepts the validity and sends the status report to the client. Any mismatch between the two, would mean a loss of the integrity of the client data at the cloud storage. If the client want to modify or delete some block information in F’ stored in the outsourced server, it send a stop signal to the TPA. TPA then stops checking and waits for the resume signal from the client. The owner prepares block information, key information and location to insert/modify the block and sends these to the server. The server after receiving the request, update the file F’. Owner then send resume signal and ask the TPA to prepare a metadata for the newly inserted block. |
| This protocol is suitable for text content only. In further research process, multimedia content in the file is separated, check the validity using the suitable algorithm and concatenated into the original file F’. |
CONCLUSION AND FUTURE WORKS |
| Cloud Computing is a relatively new-fangled concept that presents a good number of benefits for its users; However, it also raises some security troubles which may slow down its use. Understanding what vulnerabilities exist in cloud computing will help organizations to make the shift towards the cloud. Since cloud computing leverages many technologies, it also inherits their security issues. |
| In this paper, we have proposed a scheme to facilitate the cloud user in getting a proof of integrity of the data where the user wishes to store in the archive with minimum costs and efforts. The technique used for checking the integrity of the stored data and the exactness of computations done by Server and TPA is proposed. The main benefit of this method is that, storage and burden at the client side is minimal, that is, the client has to store only the encryption key information. Enhanced encryption and faster decryption is discussed. TPA is triggered to uphold the Integrity of the file F’ sporadically. |
| Our goal is not to highlight ourselves but to present a better understanding of the relative merits of this protocol and provide a beneficial protocol for supporting the data Our goal is not to highlight ourselves but to present a better understanding of the relative merits of this protocol and provide a beneficial protocol for supporting the data |
References |
|