ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Shanmuga Vadivoo. N1, Karthikeyan MA2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper an algorithm based on analytical technique is formulated for solving Dynamic Emission and Economic Dispatch using Lagrangian method. The Algorithm takes low computation time facilitating online dispatch. Emission dispatch is considered under both Static and dynamic dispatch conditions. Economic Dispatch is operated in dynamic condition. The nonlinear terms in Emission cost equation and Economic cost equation is converted into algebraic equation with the help of Taylor‟s series. The Lagrangian algorithm is used for modelling final emission equation with valve point effect and participation factor. The obtained equation is tested in MATLAB with in IEEE 30 bus 6 unit static and dynamic system with and without consideration of losses. Similarly the fuel cost equation for a 5 unit system is tested. It is observed that the results obtained from emission and economic dispatch are less than the other methods.
Keywords |
| Dynamic Economic Emission Dispatch(DEED), Lagrangian method, Valve point Effect, Ramp rate limits. |
INTRODUCTION |
| The increase in the environmental awareness and the passage of environmental regulations, the environmental constraints are having a significant impact on the operation of power systems. So the traditional economic dispatch to minimize the fuel cost is inadequate when environmental emission costs are also to be included in the operation of power plants. So utilities would like to supply power to its customers with minimum total emission as well as minimum total fuel cost. Dynamic Economic Emission Dispatch (DEED) is an extension of the conventional economic dispatch problem used to determine the optimal generation schedule of online generators, so as to meet the predicted load demand over certain period of time at minimum operating cost under various system and operational constraints. Due to ramp rate constraints of a generator, the operational constraints at any time interval„t’ may affect the operational decisions at a later hour. The typical cost function of a generator has been approximately represented by a single quadratic equation where the valve point effects are usually ignored. This would often introduce inaccuracy in the dispatch result. However, in reality the large steam turbines contribute non-convexity in the fuel cost function of the generating unit. Accuracy in the modeling of DEED problem will be highly improved when the valve point effects are taken into account. Therefore the cost curve of a generator should not be too much simplified for practical power system operation. However, the increase of accuracy of the cost function usually results in the nonlinear non smooth and non-convex function wherein the classical gradient based method fails to be applied. Since the cost of power generation cost is exorbitant an optimum dispatch saves a considerable amount of money. |
| A vast amount of literature is available which deals with the optimization of both the convex and non-convex cost function. The stochastic search algorithms such as Genetic Algorithm [8, 14], Gravitational Search Algorithm [10], Evolutionary Programming [16], Simulated Annealing, and Particle Swarm Optimization and other optimization techniques may prove to be very effective in solving nonlinear DEED problems without any restrictions on the shape of the cost curves. They often provide nearly global optimum solutions. One of the best advantages of using the traditional methods is the very small computation time it requires unlike some modern optimization algorithms which take a comparatively higher computation time. |
| This paper utilizes the computation time advantage of the traditional method and also proposes a new approach where the non-convex and non-linear cost function can also be solved using in traditional method. |
DEED PROBLEM FORMULATION |
| A. Objective function |
| Let Fi be the cost, expressed for example in dollars per hour, of producing energy in the generator unit „i’. The total controllable system production cost „F’ for N generator system is, |
 |
| ii. Real power generation limit |
| The KVA loading in a generator should not exceed a pre specified value of power because of the temperature rise conditions. The maximum active power generation of a source is limited again by thermal consideration and also minimum power generation is limited by the flame instability of a boiler. If the power output of a generator for optimum operation of the system is less than a pre-specified value of Pimin, the unit is not put on the bus bar because it is not possible to generate that low value of power from the unit .Hence the generator power Pit cannot be outside the range stated by the inequality [10] |
 |
| where Pimin is the minimum limit and Pimax is the maximum limit of real power of the ith unit at time t in megawatts. |
| iii. Generating unit ramp rate limits |
| When the demand of the system increases then to satisfy the equality constraint the power produced by the generator must also increase. The power produced by the generator cannot be increased or decreased immediately beyond a certain value owing to the fact of inertia of the rotor of the generator. So this limiting value of change in power production limit is known as ramp limit. During dynamic economic dispatch the generator power allocation must also take this constraint into account[11]. |
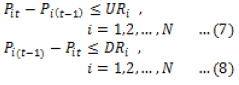 |
| where URi and DRi are the Up and Down ramp rate limits of the ith unit respectively. The power generation constraint limits given by are modified as shown below according to the ramp rate limits [11] |
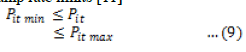 |
| such that |
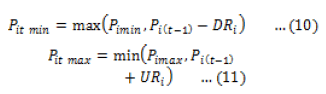 |
CALCULATION OF PARTICIPATION FACTOR BASED ON LAGRANGIAN METHOD USING TAYLOR’S SERIES |
| In order to solve the above DEED problem the nonlinear terms in the objective function (2) and (3) is replaced by algebraic equation. The objective function of the emission dispatch is taken from [9,18]. The exponential term is expanded by Taylor series with limited number of terms. In conventional methods like Lagrangian method, a consistent solution for a given economic and emission dispatch may be obtained in a very low time provided it is an algebraic equation and not a transcendental equation. In modern evolutionary computation algorithms a near global optimum solution may be achievable irrespective of the presence of any transcendental terms in the objective solution but at the cost of increased computation time. |
| The transcendental part in the emission dispatch cost function is the exponential term. The TaylorâÃâ¬ÃŸs series algebraic expansion for the exponential term is given by |
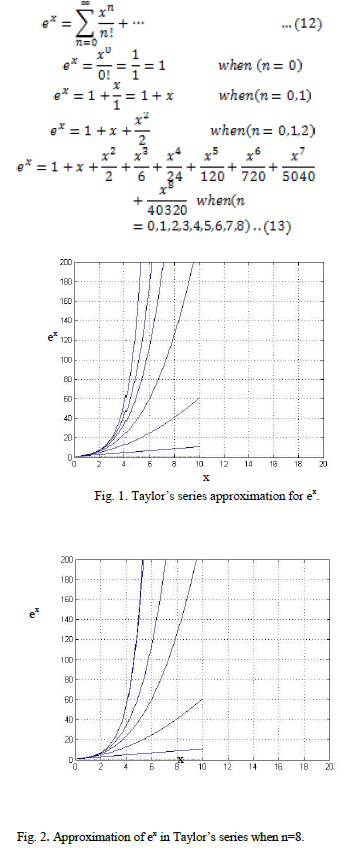 |
| The curves drawn for the expressions on the R.H.S for n=0,1,2,3,4 do not coincide with the ex curve in figure 1. In figure 2, the same curve coincides with the ex curve for the equations developed upto n=0,1,…..8. |
| Equation 13 is applied in equation 3. The exponential term is replace by the equation 13.The equation 14 is obtained as |
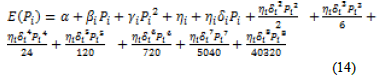 |
| The evaluation of economic dispatch cost function is as given below. The transcendental part in the economic dispatch cost function is the sine term. The TaylorâÃâ¬ÃŸs series algebraic expansion for the sine term is given by |
 |
| Figure 3 represents TaylorâÃâ¬ÃŸs series expansion of a sine curve when n=0 on x. Figure 4 represents the same expansion when the terms are expanded for n=0 up to n=9. The curves drawn for the expansion coincide with each other forming a single sine curve. |
 |
| The economic cost equation is given by Equation (2). Replacing the sine term with the TaylorâÃâ¬ÃŸs series expansion by equation (15) is applied in equation (2). |
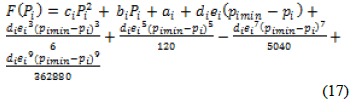 |
| The economic dispatch has to be solved repeatedly by moving the generators from one economically optimum schedule in the operating region to another operating point as the load changes by a reasonable amount. The final equation for emission and cost are obtained separately from equations 14 and 17. These equations are used to find the Lagrangian multiplier and its change. Finally the change in demand is obtained from the change in Lagrangian multiplier. From the change in demand participation factor is obtained. |
TEST SYSTEM DATA |
| The IEEE 30 bus 6 generator system is taken as test system for emission dispatch in static dispatches with and without the consideration of losses. The load on the system is 2.834 p.u. The same test system is used for dynamic dispatch with consideration of losses for 24 hour varying load. The test system used for economic dispatch is 5 unit dynamic system with the consideration of losses. |
| The IEEE 30 bus 6 unit system data required for emission dispatch for static system are taken from [1]. The data required for dynamic system are taken from [9,18]. The 5 unit system data is taken from [19] for economic dispatch under dynamic conditions. |
RESULTS AND DISCUSSION |
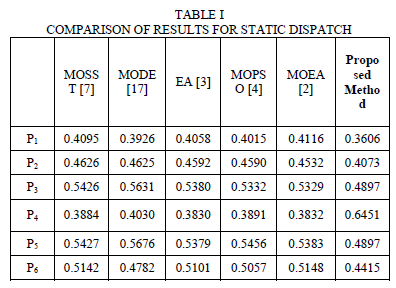
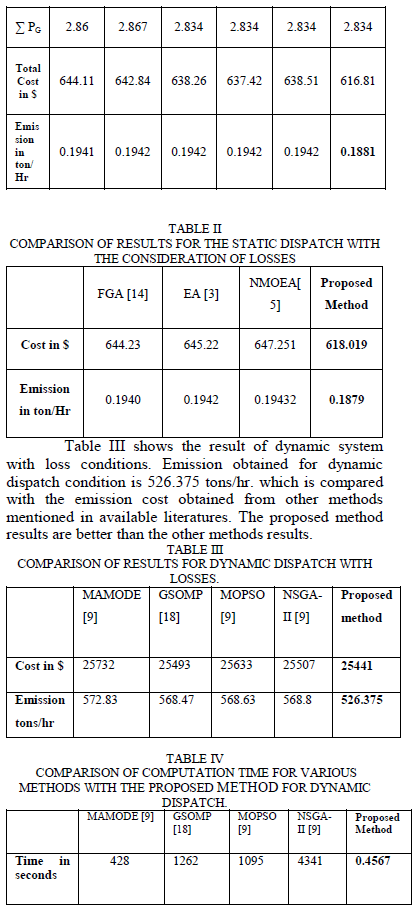
| An algorithm based on analytical technique is formulated for solving Dynamic Emission and Economic Dispatch using Lagrangian method. Emission Dispatch under both Static and dynamic dispatch conditions and Economic dispatch under dynamic condition is validated by valve point effect base point participation method. The simulation taken is compared with the available literature with results of methods like Evolutionary Algorithm [2, 3] in Table I for a loss less system. The emission and the costs obtained for the proposed method is compared with the emission in tons mentioned by other methods available and it is seen that the proposed method has the lowest emission and the cost. Obtained emission is 0.1881 tons/hr. The work is also done including loss conditions given in Table II. Obtained emission is 0.1879 tons/hr for a static with loss condition. |
 |
 |
 |
| The results shown in Table 1, 2, 3 and 4 validate the feasibility of the proposed method. Table 4 shows the comparison of computation time obtained from various methods. The comparison of computation time shown in figure 5. It shows that the proposed method has the lowest computation time. |
| The difference between the cost of the proposed method and global optimum is small when we compare the loss incurred by operating the system for the full computation time until the global optimum solution is achieved by other methods reported in the literature. Fig 5 shows the comparison of computation time for various methods reported in literature [9, 18]. |
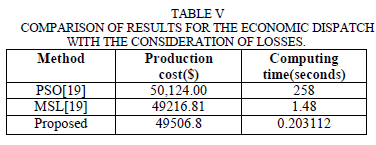 |
| Table V shows results obtained for Economic dispatch for a 5 generator system under dynamic dispatch condition. The comparison of the costs obtained from various techniques reported in literature. However, the total cost is higher than cost mentioned in MSL and lesser than PSO when compared to cost mentioned by methods but the computation time is lesser than other methods (0.20s). |
| The system is simulated using MATLAB 2013 on Intel Core i5 CPU at 2.3 GHz with 4 GB RAM capability. All computation time reported in the study are from the performance of system in above configuration. |
CONCLUSION |
| This paper has proposed a method for dynamic emission and economic dispatch. An attempt is made to find the global optimum solution by approximating the non-smooth cost curve of a generator considering its valve point effect. The feasibility of the proposed method is demonstrated using an IEEE 30 bus 6 generator system, and 5 generator system. The comparison of the obtained results with other methods in literature validates the capability of the proposed method for solving non smooth DEED problems in power systems. The method is very simple, easy to implement, convergence rate is fast and computation time is less. The performance of this approach is better in exhibiting the consistency of reaching near global optima and also guarantee on solution without violating the constraint. The proposed method is a generalized approach which can be extended to any test systems. |
References |
|