ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Ajeet Maheshwari 1 Karuna Markam 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper, we have designed the digital filter based on Bartlett window function using ANN. Firstly we have designed the 10th order digital filter based on Bartlett window function then calculate the coefficient of designed filter. We have normalized the frequency and designed filter at frequency ranges 0.05 to 1 Hz. Then we calculated the coefficients of filter at different frequencies. Some data group of coefficients is used to train the neural network designed using generalized regression algorithm and rest are used as test input to neural network. The output corresponding to test input is approximate equal to frequency corresponding to calculated coefficients using FDA tool. The optimization of the neural model has been done using generalized regression algorithm. Here radial basis function is used for the training of the neural network
Keywords |
| ANN, GRNN, NEURAL NETWORK |
INTRODUCTION |
| A filter is essentially a system or network that selectively changes the wave shape amplitude – frequency and or phase – frequency characteristics of a signal in a desired manner. Common filtering objectives are to improve the quality of a signal, to extract information from signals or to separate two or more signals. A digital filter is a mathematical algorithm implementation in hardware and/or software that operates on a digital input signal to produce a digital output signal for the purpose of achieving a filtering objective. A simplified block diagram of a real-time digital filter, with analog input and output signal is as shown in figure.1 |
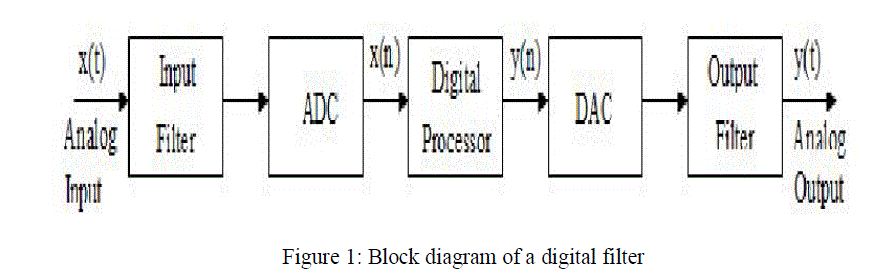 |
| Filter designing is the process of transformation of input sequence to obtain desired output sequence. Filter designing process can be described as an optimization problem where each requirement terms to an error function which should be minimized. Digital filter are of two types, Finite Impulse Response (FIR) filter and Infinite Impulse response (IIR) filter. In this paper the concept of Artificial Neural Network, which is also a wide area of research? The main goal of the design is to find the recursive coefficients that define the filter transfer function. In this research work, DSP a neural networks were combined to produce an excellent algorithm for digital filter design In the previous work, the fir filter was designed by least square method and frequency sampling method. MLP and RBF algorithm were used to train the neural network model. The efficiency of these above method is about 93%, but when generalized regression algorithm is used the accuracy is about 98%. That is the advantage of this method. |
DESIGN FIR FILTER USING WINDOW METHOD |
| The windowing method requires minimum amount of computational effort; so window method is simple to implement. For the given window, the maximum amplitude of ripple in the filter response is fixed. Thus the stop band attenuation is fixed in the given window, but there is some drawback also of this method. The design of fir filter is not flexible. The frequency response of fir filter shows the convolution of spectrum of window function & de-sired frequency response because of this; the pass band & stop band edge frequency cannot be precisely specified. In this work we use Bartlett window method. |
LITERATURE SURVEY |
| Awadhesh Gupta et. al. Presented a paper on design and analysis of low pass FIR & IIR filter and find optimum result using neural network. Author designed the low pass FIR and IIR filter and tried to reduce the number of side lobes and compact the size of main lobe then compared the result with filter designed using neural network. Filter designed using neural network gives the better result as compare to conventional method of design. |
| Harpeet Kaur et. al. presented a paper on design of low pass FIR filter using artificial neural network. Author design the low pass FIR filter based on Keiser window function. The stop band attenuation (SBT), transition width (TW),pass band ripple(PBR),sampling frequency and filter length are the varying parameter. This work is carried out using 30such values of all the varying parameter. Trained the same filter using neural network. The filter coefficient can be easily calculate using some known parameter of filter . |
| Navneet Gupta et. al. presented a paper on design low pass filter using generalize regression neural network. Author design the rectangular window in FDA tool of MATLAB and calculate the coefficient of designed filter corresponding to cut off frequency. Then trained the neural network using data collected from FDA tool. The accuracy of coefficient corresponding to cut off frequency using neural network is better than designed filter in FDA tool. |
ARTIFICIAL NEURAL NETWORKS |
| An Artificial Neural Network (ANN) also known as “Neural Network (NN)” is a computational model based on the structure and function of biological neural network. In other words ANN is computing system which is made up of a number of simple processing elements (the computer equivalent of neurons, Nodes) that are highly interconnected to each other through synaptic weights. The number of nodes, their organization and synaptic weights of these connections determine the output of the network. ANN is an adaptive system that changes its structure/weights based on given set of inputs and target outputs during the training phase an produces final outputs accordingly. ANN is particularly effective for predicting events when the network have a large database of prior examples to draw. The common implementation of ANN has multiple inputs, weight associated with each input, a threshold that determine if the neuron should fire, an activation function that determine the output and mode of operation. The general structure of a neural network has three types of layers that are interconnected: input layer, one or more hidden layers and output layer as shown in Figure 2. |
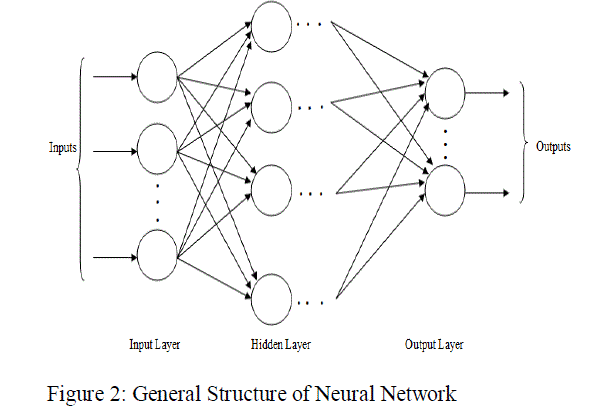 |
| There are some algorithms that can be used to train an ANN such as: Back Propagation, Radial-basis Function, and Support Vector learning, etc. The Back Propagation is the simplest but it has one disadvantage that it can take large number of iterations to converge to the desired solution [3]. In Radial Basis Function (RBF) network the hidden neurons compute radial basis functions of the inputs, which are similar to kernel functions in kernel regression. Speech has popularized kernel regressions, which he calls a General Regression Neural Network (GRNN) [3]. General Regression Neural Network (GRNN) is a variation of Radial Basis Function (RBF) network that is based on the Nadaraya – Watson kernel regression. The main features of GRNN are fast training time and it can also model nonlinear function. GRNN being firstly proposed by Sprecht in 1991 is a feed forward neural network model base on non linear regression theory. It approximates the function through activating neurons. The network structure of GRNN consists of three layers: input layer, radial basis hidden layer and linear output layer as shown in Figure 3.The transfer function of hidden layer is Radial Basis Function. |
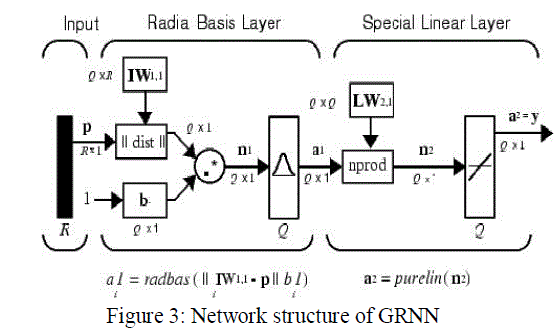 |
FORMULATION OF PROBLEM |
| The aim of this paper is to estimate the cut off frequency of any given coefficients of fir filter and increase the accuracy of result from previous work. Accuracy is determined by com-paring the result from fdatool and nntool. For training purpose we use input output dataset derived from fdatool, and for testing purpose we use a test input and simulate it using nntool. |
METHODOLOGY |
| In this methodology we use Bartlett window technique for filter designing and generalized regression neural network for training purpose. |
Step 1 |
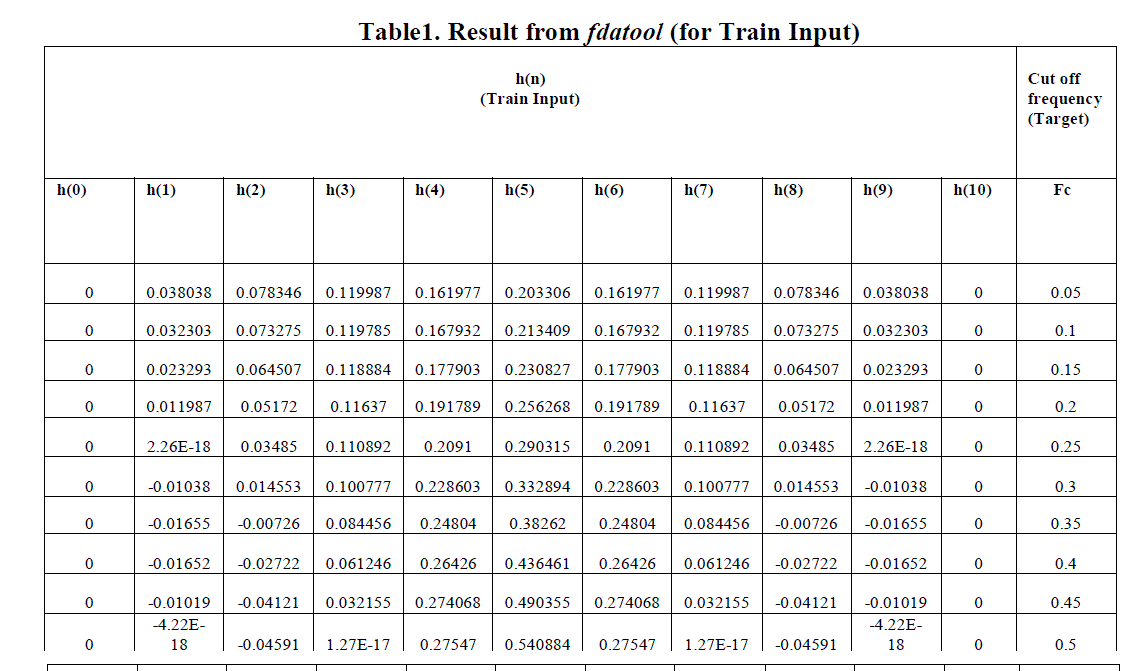
| Low pass fir filter designed by fdatool. The order of filter is 10. We use cut of fre-quency ranges from 0 to 1. Then set the value of fc=0.05 and design the filter. Repeat the same process for value of fc from 0.1 to 1. So this gives the 19 dataset of input and output data. Out of these 19 dataset we use 17 for training and 2 for testing. Here input is h(n) and output is fc. The screenshot of first step is given below in Figure 3 |
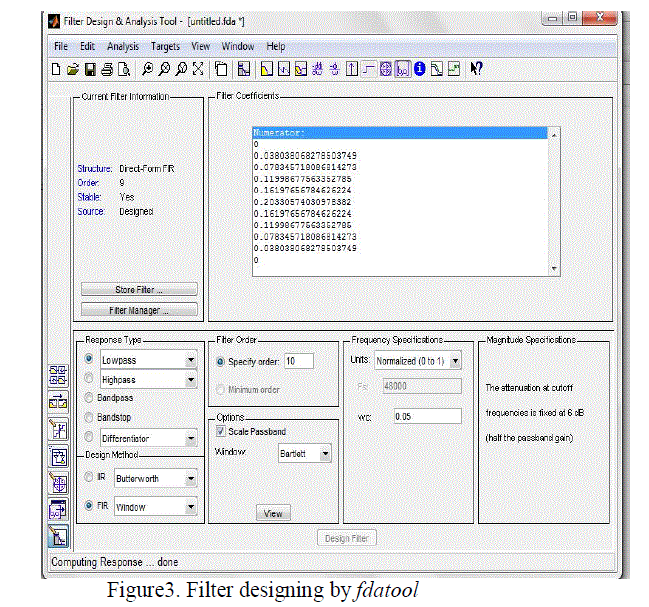 |
Step 2 |
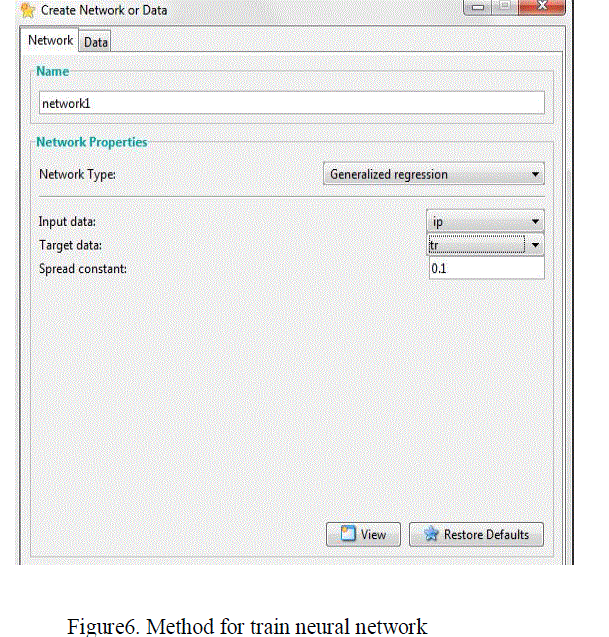
| In this step we design the neural network model by nntool shown in Figure 5. Train-ing is done by GRNN and spread constant is set to 0.1. After training, simulate the network by testing input shown in Figure 5, 6 and the simulation result shown in Figure 7. |
 |
 |
RESULTS AND DISCUSSION |
| In the above experiment, According the Table 2: (Result from fdatool) For the test input h(n), the output fc is 0.55 & 0.85. this result is deduce from filter designing tool. According to the Table 3: (Simulation result from nntool) the output for the same test input h(n) is 0.5537 & 0.83923. This result is taken from neural network tool. So the results from nntool and fda-tool are nearly same, and by this process we can easily estimate the cut off frequency of any fir filter |
 |
 |
CONCLUSION |
| From this experiment we estimate the cut off frequency and other parameter from filter co-efficient by the help of GRNN, and it is quite simple method than complex calculative window method. The above figures show that results come from Bartlett window method and artificial neural network is almost same. For the filter designing purpose This GRNN training algorithm is much better than other training algorithm like MLP, RBF etc. In the previous work, when MLP is used as a training algorithm, result is about 93% accurate. By the using of generalized regression algorithm, the accuracy of result is almost 97%. So there is increment of 5% in accuracy, which is very effective. |
References |
|